论有效应力原理的前世今生

2023-01-07王国义

重庆建筑 2022年12期

王国义

（中电建成都建设投资有限公司，四川成都 610212）

0 引言

J.K.Mitchell 认为太沙基关于饱和土体的有效应力原理是土力学的“拱心石”，经典土力学中的太沙基一维渗流固结理论、比奥固结理论、土的排水与不排水强度及其指标、渗透变形、地基的预压渗流固结等许多课题，都是建立在有效应力原理基础上的。太沙基的有效应力原理也是土力学能够成为一门独立的力学学科的标志性理论[1]。但针对太沙基有效应力原理的适用性，越来越多的专家学者提出质疑，并提出自己的观点，希望达到“水土分算”与“水土合算”的统一。方玉树先生[2]1991 年开始提出水压率理论，并始终如一坚持至今。笔者[3-7]2020 年由于探讨盾构土仓保压问题研究土力学，偶然间引入岩土给水度并通过力平衡原理推导出新有效应力原理公式，持续对该问题进行探讨。

本文基于已有研究，对太沙基有效应力原理、水压率理论和新有效应力原理进行分析，以期推动理论土力学的发展。

1 太沙基有效应力原理的建立与争论

太沙基[8]在《理论土力学》一书中提出了有效应力原理。在无凝聚性土（砂性土）上方加入一定高度的水，土层无可觉察的压缩（图1），另一方面，如果将铅丸放在土层表面上（图2），土层会压缩变形。对于凝聚性土（黏性土）孔隙水压力对其的应力、应变与抗剪强度之间关系的影响，可以借圆柱形试样用三轴压缩试验的方法来加以研究，因为试验的装置允许同时测定总应力和中和应力。

图1 表现有效应力和中和应力差别的试验装置

图2 铅丸导致饱和土体变形示意图

据此太沙基提出了有效应力原理公式：

式中：σ——竖直总应力，kPa；σ′——平面上有效法向应力（土骨架应力即有效应力），kPa；uw——孔隙水压力，kPa。

太沙基有效应力原理主要结论如下：一是孔隙水压力是中和应力，中和应力对土体的变形和强度无影响；二是土的有效应力等于总应力减去孔隙水压力；三是土的有效应力控制了土体的变形及强度；四是有效应力原理适用于砂性土和黏性土。

但实际应用中砂性土水土压力计算（水土分算）与太沙基有效应力原理相符，而黏性土水土压力计算（水土合算）与太沙基有效应力原理不相符。大部分研究者都认为砂性土适合水土分算，黏性土适合水土合算。太沙基有效应力原理支持者认为该原理对于砂性土和黏性土都适合，而质疑者认为该原理只适合砂性土不适合黏性土，因此导致针对太沙基有效应力原理的争论不断，甚至有些学者希望能够找到一合适公式，实现水土压力分算与合算的统一。但由于提出的公式基本都与太沙基有效应力原理一样，不是理论推导出来的，无法得到普遍的认可。

2 水压率理论的提出

方玉树先生[2]提出水压率的概念，在水压率基础上修正了孔隙水压力、浮力、浮重度、渗透力、固结系数和贮水率计算方法，并对渗流破坏、基坑突底和振动液化特征作出了解释。

水压率理论表达式为：

式中：σ——竖直总应力，kPa；σ′——平面上有效法向应力（土骨架应力即有效应力），kPa；u——孔隙水压力，kPa；ζ——水压率，饱和土截面上自由水面积率；γw——水重度，kN/m2；h——压力水头，m；μ——土的给水度；n——土的孔隙度。

方先生提出水压率理论建立的基础是：孔隙水压力是单位面积土截面上的水压力；孔隙水压力（及总应力和有效应力）所涉及的截面是在颗粒（或胶团）之间通过的，宏观上是平面的曲面；结合水不传递水压力。方先生提出水压率理论后，李广信先生[9]对其提出了质疑，坚持太沙基有效应力原理的正确性。

笔者认为方先生对其水压率理论坚持至今，主要是因为他确实将现今的水土分算与水土合算公式联系了起来，形成了水土压力的统一计算。如果砂性土中自由水占水的绝大部分的水土分算和黏性土中只有强结合水与弱结合水的水土合算理论上都是正确的，那么方先生的水压率理论应该就是正确的，只是水压率值的计算也是估算。而水压率理论与水土分算和水土合算一样无理论基础，不是推导出来的。

3 力平衡原理下的有效应力原理

笔者认为黏性土中的弱结合水不能产生并无损耗传递静水压力（图3），应该纳入土骨架范围，只有重力水能够产生并无损耗传递静水压力，作为自由水存在。因此，只认为自由水是各向同性的，强结合水、弱结合水与土颗粒一起构成土骨架，具有各向异性特征，计算静止侧压力时乘以侧压力系数K0。

图3 只含强弱结合水的黏性土

笔者通过力平衡原理（图4），推导出新有效应力原理公式：

图4 饱和土截面示意图

推导水平截面自由水通道面积，是从如图5 的解释向如图6转变的过程，实际上每个水平截面都是应该有自由水通道面积的，那么土骨架和自由水分开简化示意图应如图6 所示，自由水体积是水平截面自由水面积的叠加。

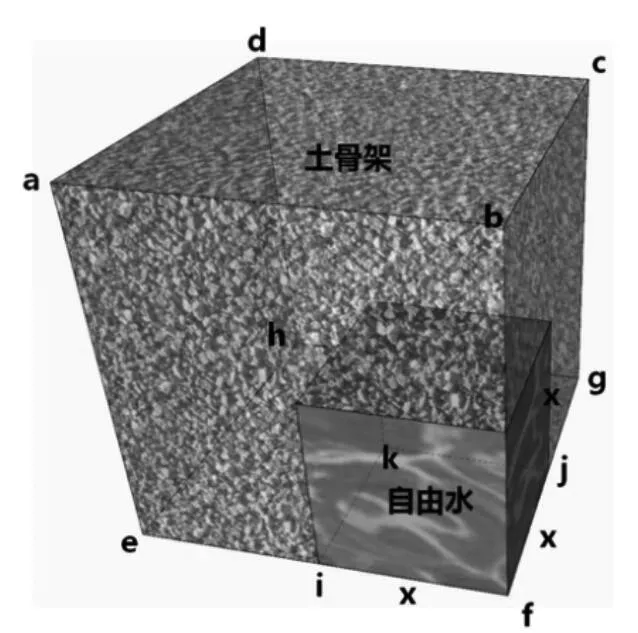
图5 饱和土体土骨架与自由水分开简化示意图1

图6 饱和土体土骨架与自由水分开简化示意图2

新有效应力原理修正后的公式为：

式中：σ——竖直总应力，kPa；σ′——平面上有效法向应力（土骨架应力即有效应力），kPa；μ——土的给水度；uw——孔隙水压力，kPa。

按照现今水土静止侧压力的理解，式（6）推出的水土静止侧压力公式为：

式中：σ侧——静止侧向总应力，kPa；σ′——平面上有效法向应力（土骨架应力即有效应力），kPa；k0——静止侧压力系数；μ——土的给水度；uw——孔隙水压力，kPa。

4 水土侧压力计算公式的探讨

计算基坑静止侧压力时，土骨架面积上基坑侧是无孔隙水压的（图7），基坑外侧的孔隙水作用力是无内侧孔隙水作用力平衡的，那么基坑侧的支撑力需额外增加作用力平衡基坑内侧土骨架面积上所承受的孔隙水作用力的传递力。

图7 基坑侧土颗粒力平衡示意图

孔隙水侧压力通过土颗粒传递到基坑内侧，孔隙水作用力通过土颗粒的传递（传递距离不同）是要减弱的。设孔隙水作用力在土颗粒上的传递系数为k，那么就可计算出基坑支护饱和土水土侧压力：

对于σ1的求解可以理解为截面上方孔隙水对截面的平均应力为kuw+（1-k）μuw，那么就可求出土骨架应力：

式（8）、式（9）中：σ侧——基坑支护静止侧向总应力，kPa；σ1——平面上法向应力（土骨架应力），kPa；k0——静止侧压力系数；μ——土的给水度；uw——孔隙水压力，kPa；k——传递系数；σ——竖直总应力，kPa。

当传递系数k 为1（即作用力传递无减弱，如砂性土）时，σ侧=k0σ1+uw就是现今的水土分算计算公式；当给水度μ为0（即无孔隙水，如黏性土）时，σ侧=k0σ1就是现今的水土合算计算公式；当k为0、μ不为0 时，σ侧=k0σ1+μuw就是式（7）。因此，式（7）也是岩土静止侧压力式（8）的一个特例，式（8）才是适用于所有类型岩土的静止侧压力计算公式。

式（8）的理论推导，说明水土分算公式和水土合算公式都是有理论基础的，太沙基有效应力原理计算水土侧压力是水土侧压力计算的一个特例。当然传递系数k 应通过试验或经验确定，水土静止侧压力值的准确性取决于静止土压力系数k0和传递系数k，传递系数k 如何取值还需进一步探讨。

5 有效应力计算公式的探讨

太沙基认为有效应力能对土体产生可觉察的影响或使土体的抗剪强度增加，也就是说当有额外荷载增加，土体将变形，变形稳定后有效应力增加，增加的有效应力应等于额外荷载的平均应力。有效应力增加后土体的抗剪强度也会增加。对于饱和土，当荷载增加、土体变形，土中水将被挤走，截面上的土颗粒面积增加，同时抗剪强度增加；对于非饱和土，当荷载增加、土体变形，土骨架将变得更加密实，截面上的土颗粒面积增加，同时抗剪强度增加。通过上述分析，笔者认为有效应力应该是截面上土颗粒所承受作用力在总截面上的平均应力（式10）。有效应力与承载力成正比关系，有效应力越大，承载力越大。当土体孔隙率为0 时，有效应力最大，承载力也最大。

有效应力计算公式：