一类二阶有理差分方程的解的性质

黄日娣，全卫贞，周敬人，王 丽

（1.湛江幼儿师范专科学校数学系，广东湛江 524037；2.岭南师范学院基础教育学院数学系，广东湛江 524037）

随着现代科技的飞速进步，差分方程在经济学、生态学、工程学、物理学、数学、计算机等多个领域都有着广泛的应用，人们日益重视差分方程的研究，现在它已成为现代数学的一个重要分支.

有理差分方程性质的研究近年来引起广泛的关注[1-12].Sedaghat[3]研究了有理差分方程xn+1=(n=0,1,2,…)的解的渐进性.陈云[4]研究了几类有理差分方程xn+1=axn+的解的性态.骆元媛等人[5]研究了有理差分方程(n=0,1,2,…)的奇点集和解的渐近性.

受上述研究启发，本文研究下述二阶差分方程的解的渐近性：

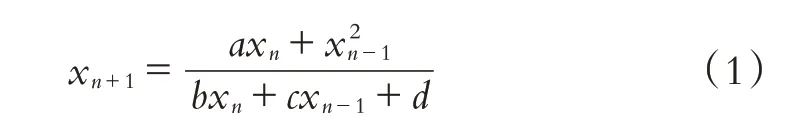
其中a,b,c,d∈R+，初始值x-1,x0∈R+，n=0,1,2,….

1 预备知识

定义1如果满足，称是差分方程（1）的平衡解.

定义2由二阶差分方程xn+1=f(xn,xn-1)，可得函 数f(u,v).令a0=fu(,)，a1=fv(,)，可 得 特 征方程：

由此求出特征根.

定理1[1]①若特征方程（2）两个根的绝对值都小于1，则差分方程（1）的平衡解是局部渐近稳定的；②若特征方程（2）至少有一个根的绝对值大于1，则差分方程（1）平衡解是不稳定的；③若特征方程（2）没有模为1的根，则差分方程（1）的平衡解为双曲的，否则称为非双曲的；④若平衡解为双曲的，且特征方程（2）存在一个根的绝对值大于1，一个根的绝对值小于1，则差分方程（1）的平衡解为鞍点.

定理3（Routh-Hurwitz判别法）[6]假设实系数多项式方程p(λ)=a0λn+…+an-1λ+an=0（其中a0＞0），则其所有根具有负实部的充要条件是Δk＞0(k=1,2,…,n)，其中Δk是n阶矩阵的k阶主子式.

定理4（Schur-Cohn判别法）[6]方程p(λ)=a0λn+…+an-1λ+an=0的所有根满足的充要条件是方程所有的根具有负实部.

2 主要结果

可用差分方程的动力学定理、Routh-Hurwitz和Schur-Cohn判别法这两种不同方法研究二阶差分方程（1）的解的渐近性.

定理5 ①若0＜＜1时，差分方程（1）的平衡解=0是局部渐近稳定的；②若＞1时，差分方程（1）的平衡解=0是不稳定的；③若a=d时，差分方程（1）的平衡解=0为非双曲点.

定理6考虑平衡解=，则有：

①当a(3c+b-3)＞d(c-b-1)且a(b+2)＞d(3-c )时，平衡解为局部渐近稳定（此平衡解称为汇点）.

②当a(b+2)＜d(3-c)，或a(2c+b-2)＞d(c-1)且a(3c+b-3)＞d(c-b-1)时，平 衡 解=

不稳定（此平衡解称为排斥点）.

定理7用Routh-Hurwitz和Schur-Cohn判别法得到差分方程（1）的如下结论：