基于RSSI的多项式变参数室内测距算法*

王险峰 郭光亿 赵 玲 邱祖泽 丁子琳

（东北石油大学计算机与信息技术学院 大庆 163318）

1 引言

接收信号强度指示（RSSI）是对设备可以从其他对等端设备或基站检测和接收信号的质量的估计度量。当信号传播更大的距离时，信号变弱，这使得无线设备通过无线信号强度判断与目标设备间的距离成为可能。利用RSSI进行测距的模型分为大尺度模型和小尺度模型两类［1］。小尺度模型可以刻画由多径效应、衍射等引起的短距离（通常不长于若干波长距离内）内接收信号强度经历的剧烈变化，更适合室内测距应用场景。

使用RSSI进行三角定位的基本步骤为根据接收信号最强的几个锚节点的位置坐标计算被估节点的位置坐标［2］。由于实测RSSI信号同时存在随机和系统性误差，对RSSI测距模型进行改进是必要的。文献［3］利用了两个不同位置的接收节点，利用其接收信号强度的差异构造权重向量抑制了RSSI误差；文献［4］提出了一种梯度预测滤波器过滤RSSI时间测量信号中的波动；文献［5］设计了一种特殊形状的天线，将其应用于实验室鼠笼内小鼠的定位，取得了不错的效果；文献［6］利用了RSSI测量值与距离值之间的相关性，建立了两者之间的概率模型；文献［7］则将一般的RSSI模型中的环境参数也看作变量，以此引出了环境适应性模型。文献［8］将定位误差问题表述为约束非线性规划问题，但并未直接改进测距模型。文献［9］训练并使用反向传播（BP）神经网络拟合RSSI距离曲线。文献［10］发现在误差项影响下曲线走向随距离增大而偏离传统负对数曲线越远。

由于RSSI信号在较短距离内的剧烈变化，文献［11］认为室内环境下仅凭RSSI单一指标无法实现可靠的测距和定位，文献［12］认为RSSI并非作为无线网络定位工具的良好指标。针对这一点，文献［13］提出了可靠分析定位应用中RSSI特征的方法。分析结果显示不同型号开发板之间的差异相比不同环境中的同型号开发板之间的差异对RSSI数据可重复性的影响更大。

本文的研究沿袭文献［7］的变参数环境适应模型思路与文献［10］对误差项对曲线走势的影响的发现，在这两篇文献的基础上通过建立物理模型和拟合实验数据得出新的RSSI测距模型。

2 电磁传播模型

2.1 自由空间模型

长度为l的单极子天线，内部均匀分布电流I，则在以天线中心为原点，天线方向为z轴的球坐标空间某点（r，θ，φ）的电场强度E、磁场强度H分别为［13］

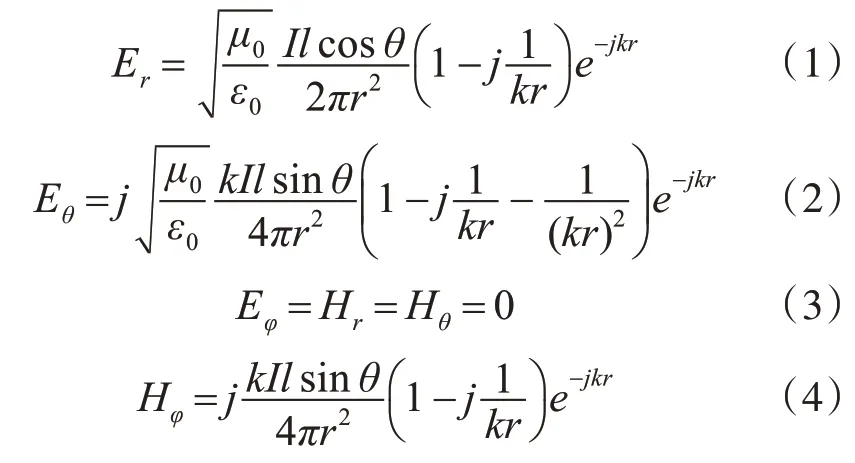
其中μ0，ε0为真空中磁导率与介电常数，k为波数。电磁场辐射能流密度为波印廷矢量幅值。

根据共轭复数乘法分配律计算得到平均坡印廷矢量：

即平均能流密度沿r方向，幅值随距离平方衰减。Sc为与方位有关与距离无关的参数。

单极子天线辐射穿过以原点为中心半径为r的球面的电磁能量为

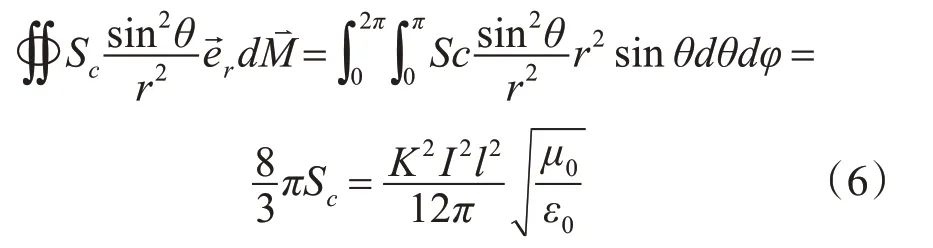
该结果与天顶角θ及半径r均无关，这说明在无电磁反射表面的自由空间中，理想单极子天线电磁能量辐射满足球面传播模型。

2.2 反射与衍射

实际环境由于障碍物的存在会导致电磁信号产生反射和衍射，且直射波与反射波、衍射波产生干涉叠加，导致其不再符合简单的球面传播模型。根据文献［14～17］：

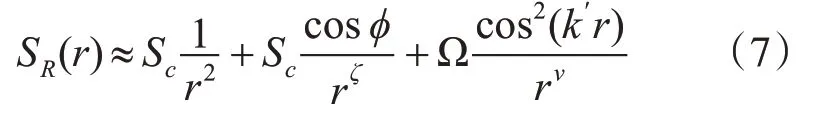
其中Ω为只与环境遮挡物位置及方位有关与距离和光程无关的参数。

2.3 对shadowing模型的改进

记设备在距离d时的接收功率为P（d），根据shadowing模型：

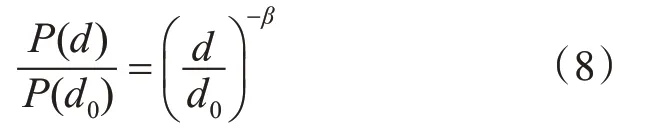
此处省略了随机误差项。由于室内障碍物往往按照一定规则进行摆设，其对信号带来的影响无法用简单高斯分布描述。考虑前文所述信号的反射、直射信号与反射信号的干涉及信号源与设备间的衍射效应，上式应该加入不同次幂的项：

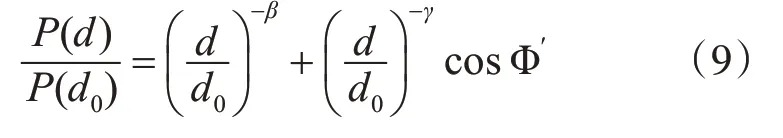
式中β、γ均为正实数，但均不一定为整数。其多项式逼近为

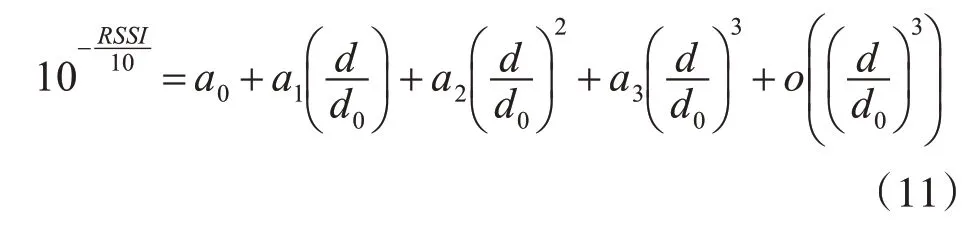
2.4 变参数动态测距算法

考虑到某处信号强度的分布与该处的环境特征有关，我们在式（11）的基础上引入了参数调整机制形成变参数测距算法。首先根据拟合值初始化模型参数。当RSSI值出现变动时，根据当前时刻参数模型计算距离，结合前一时刻计算得到的距离计算速度即距离变化率。根据物理限制（设备间相对移动速度），若计算得到的距离变化率处在合理范围内，可认为环境未发生明显变化，RSSI的变化是由距离变化引起，无需调整参数。反之则认为是环境条件变化导致，此时应根据一定的方式调整模型参数。

3 仿真实验

3.1 仿真实验设计

我们设置了如图1所示的模拟房间，区域F2为自由空间，区域F1，F3为模拟均质墙壁。求解如下关于电场强度的方程：

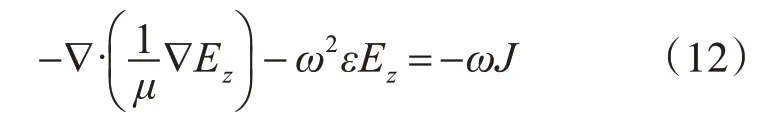
图1 模拟房间几何构成

根据电场强度的解由模拟条件的特性可根据下式计算模拟区域内电磁场能流密度：

最终得到模拟辐射能流密度对数分布：

其中δ为一极小正浮点数，用于消除当S=0时产生的“非数值”（NaN）计算结果，简化后续编程工作。模拟辐射能流密度对数与RSSI之间存在线性关系，因此可将该值作为模拟RSSI值看待。模拟场RSSI的分布如图2所示。

图2 模拟辐射场分布

以模拟信号源为中心，向随机方向选取若干等长线段，求取其模拟场强值，将与模拟源等距离处的数值取平均得到平均值趋势线，对其分别使用两个公式进行最小二乘拟合，同时得到两公式各自参数的拟合值及误差等数据。比较结果如表1所示。

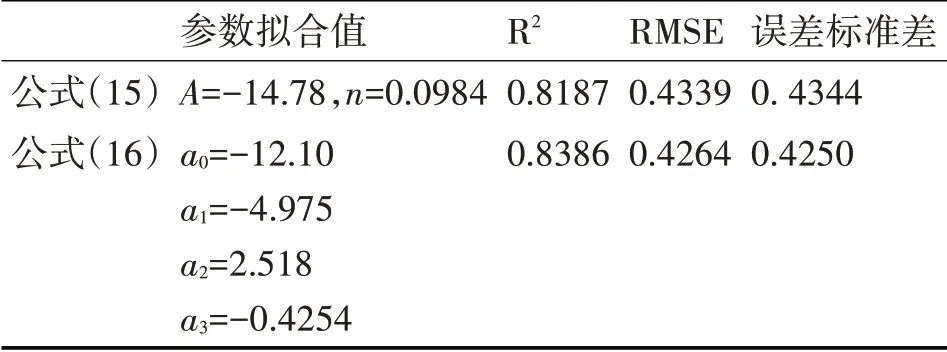
表1 模拟曲线拟合参数

公式（15）：RSSI（d）=A-10nlog（d）

公式（16）：RSSI（d）=a0+a1d+a2d2+a3d3，参数约束

可以发现，多项式公式（公式（15））的拟合程度高于负对数公式（公式（16）），同时其拟合误差及误差波动程度也小于负对数公式。

在仿真过程中，为更贴近实际，我们假想有一机器人，沿一预定路线匀线速行走，行走过程中机器人实时计算自身与发射源的距离，行走结束后记录计算结果并与真实值比较。

3.2 仿真实验结果

图3是根据不同测距算法逆推得到的机器人运动轨迹与实际路线的对比。表2给出了不同距离模型的相对误差平均数与标准差。

表2 不同算法相对误差比较

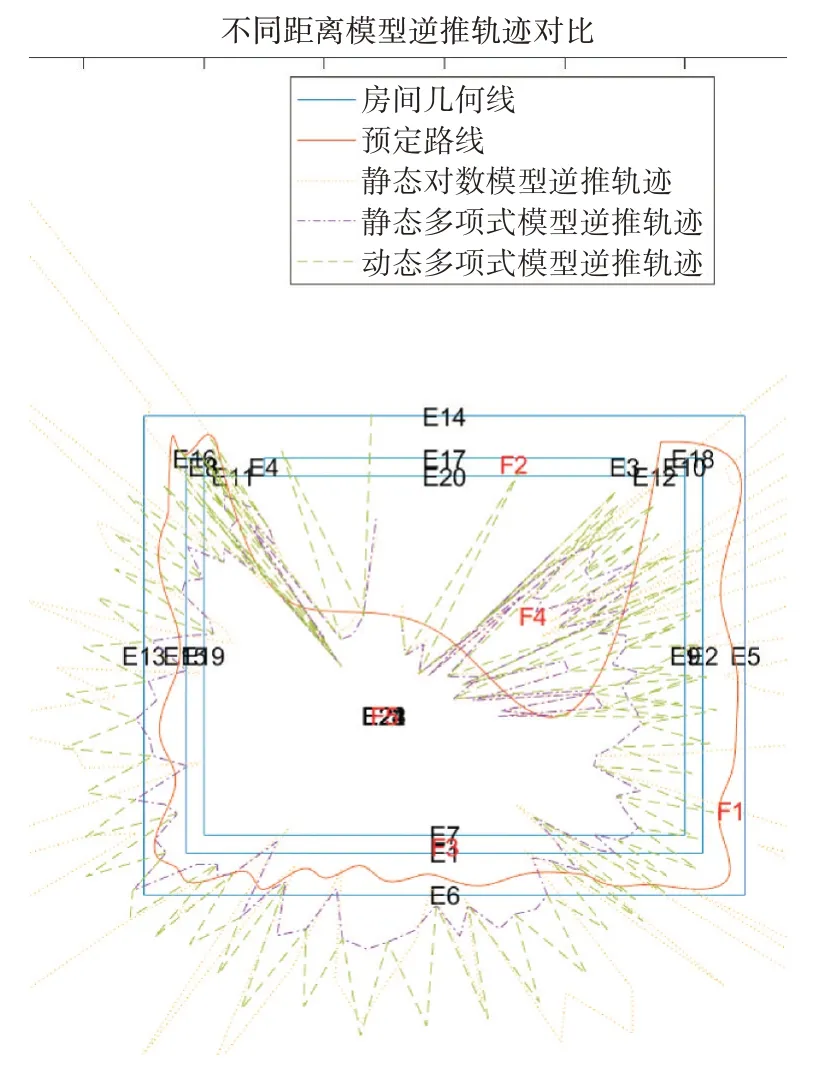
图3 不同算法逆推轨迹对比

可以看出，在室内条件下，多项式算法的测距误差和稳定性要优于负对数算法，多项式算法中动态算法整体表现优于静态算法。

4 结语

通过对无线信号的电磁传播进行建模，本文得出了不对环境信息进行假设的信号强度—距离模型，并通过数据拟合对比发现我们的模型略强于传统的负对数模型。但同时我们也发现由于RSSI本身的剧烈变化，使其无法作为无线网络测距和定位算法的可靠指标。针对这一点本文提出了一种自适应的距离计算模型，在RSSI测量误差无法预测的情形下，将模型中的部分参数也当做变量，基于合适的数据过滤规则调整参数值，控制了环境因素变化导致的系统性噪声对距离测算的干扰。

经过仿真实验发现，室内条件下多项式模型的精度与稳定性优于对数模型，动态模型整体精度优于静态模型。动态多项式模型的相对误差标准差高于静态多项式模型，这说明参数调整策略的选择会影响模型误差的稳定性，其具体影响有待进一步研究。

同时通过求解偏微分方程，仿真实验也发现，与其他文献对数据扰动仅归因于随机干扰的解释不同，即便在由假想均匀材质墙壁围成，只存在两扇门，无人为噪声信号分布的简单模拟房间内，由于墙壁对信号的反射以及直射信号与反射信号的干涉也足以对辐射场的空间距离分布曲线产生宏观随机的显著扰动。