城市轨道交通PPP项目运作方式选择研究

2023-01-06李志杰张晶淇邵志国

青岛理工大学学报 2022年6期

赵辉，李志杰，张晶淇，邵志国,2

(1.青岛理工大学管理工程学院，青岛 266525；2.同济大学可持续发展与新型城镇化智库，上海 200092)

随着大量人口迁入城市定居，造成城市区域面积和人口数量集中度的双重扩张，交通问题成为制约城市生产扩大和经济提高的主要问题[1]。轨道交通的能耗低、运输量大、安全快捷，解决城市扩张带来的交通问题具有天然优势。但是，轨道交通项目投资规模大，运作成本高，政府债务压力沉重，国内外学者致力于引进不同的项目运作方式来开拓融资渠道。其中，公私合营(Public Private Partnerships，PPP)模式[2-4]在国内外备受推崇。PPP模式的运作方式诸多，选择与项目最为匹配的运作方式，才能真正解决政府财政负担的难题[5]。有学者认为，项目特点、风险分担、政策环境、融资渠道、所有权归属等因素是PPP项目运作方式决策的重要指标[6-8]。本文分析了PPP项目的定义，总结了PPP运作方式的适用范围和交易框架[9-10]。另外，一些学者还使用各种数学方法，如分级分析法、自组织映射神经网络法、灰度相关分析法、模糊(QFD)方法和TOPSIS法等[11-13]；除此之外，很多学者还讨论了对港口、收费公路、综合管理走廊、废矿山、保障性住宅等项目的运作方式选择[14-15]。前人研究大多为定性分析，极少定量研究；仅采用单一决策模式，没有结合项目实际进行探讨。有些文献是实证研究，但仅针对单个项目，由于对PPP模式的分析没有与所有运作方式联系，所以难以形成完整的评估体系，且没有实际的参考价值。项目的运作方式关系到项目能否顺利实施，需要建立完整的评估系统，根据项目的实际情况决定合理的方案。因此，本文旨在分析轨道交通PPP项目的运作方式，为轨道交通PPP项目的运作方式决策提供参考。

1 PPP项目运作方式的分类及特征

基于发改委及财政部相关PPP项目运作方式的具体分类要求[16]，参照当前PPP模式的具体应用表现与实际情况的差异性，将运作方式具体区分为下述类型，并从资产所有权以及经营属性等五个层面入手，分别对不同运作方式的主要特征进行了比较，见表1。

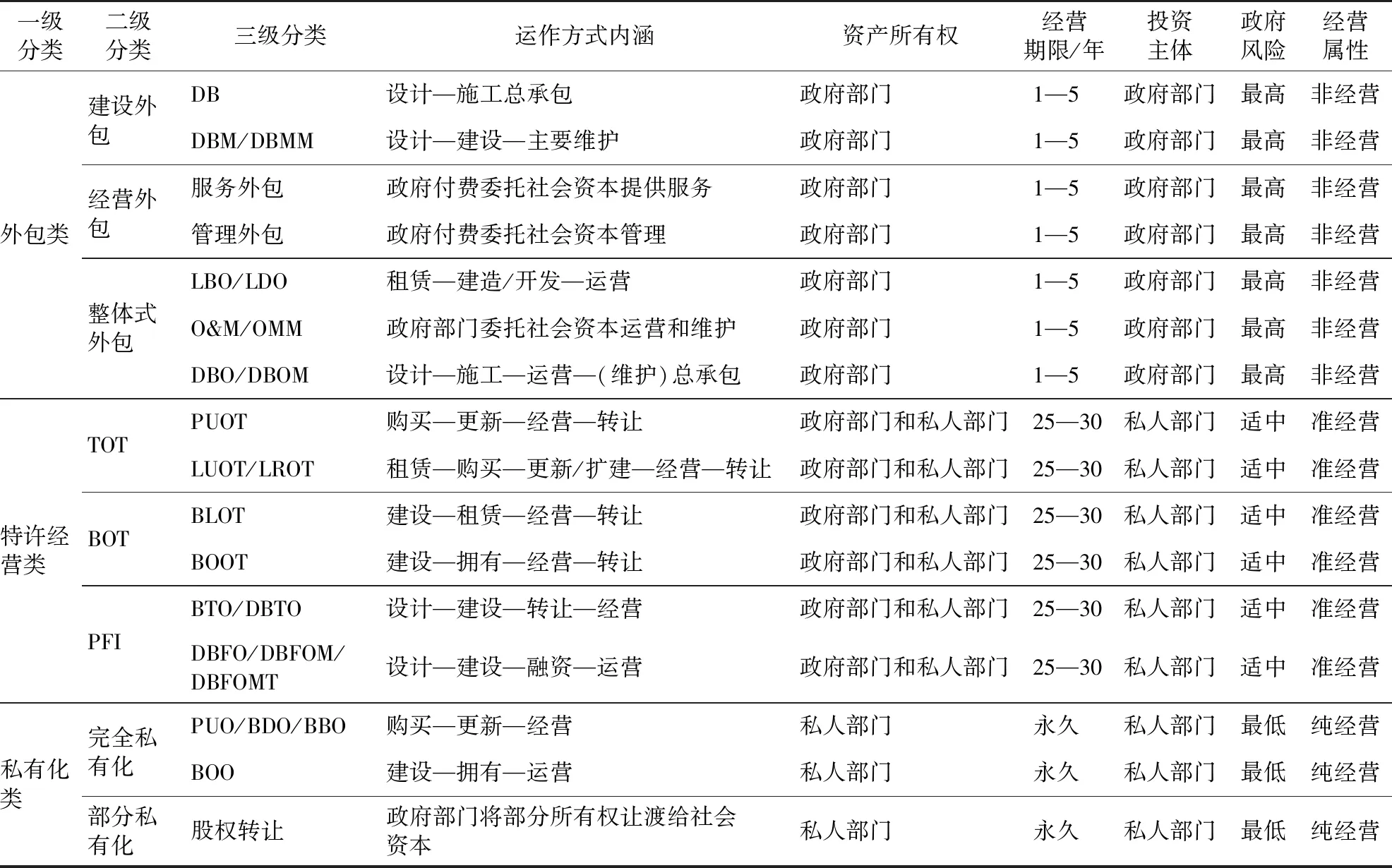
表1 PPP项目运作方式分类及特征

2 基于两层次决策模型的PPP项目运作方式初选

政府与民营企业的合作关系是PPP项目的核心，政府与民营企业关系的多样，决定了PPP项目的运作方式多样，PPP模式的基本结构如图1所示。

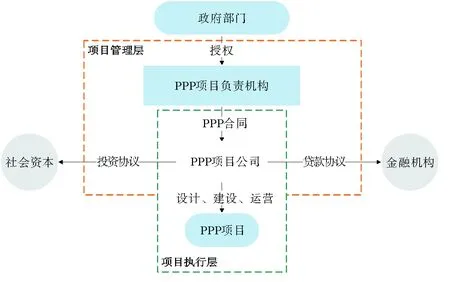
图1 PPP模式的基本结构

PPP模式分为项目管理层和项目执行层两个结构层。政府和项目公司通过PPP合同在管理方面确定权利和利益的分配，通过设计、建设、运营合同解决PPP项目的运作。轨道交通项目作为准经营性基础设施项目，有收费机构和资金流入，收费仅占投资的一部分。因此，这些项目既可以特许经营方式经营，也可以采用部分外包的方式经营。

3 基于GRA-VIKOR法的运作方式终选

3.1 指标体系的构建

在选择城市轨道PPP项目的运作方式时，轨道交通不仅要考虑到公共基础设施有关的共有因素，而且还需要联系项目特征以及区域特征遴选出具备良好适应性的分析指标。基于此，本文对从事轨道交通和PPP项目研究工作的专家及部门展开问卷调查，发出问卷120份，回收有效问卷107份。对问卷进行处理后，选择出相关性以及冗余性较高的指标，进而建立由12个指标构成的决策指标体系，见表2。

表2 轨道交通PPP项目运作方式决策指标体系

3.2 轨道交通PPP项目运作方式决策模型

在选择轨道交通PPP项目的运作方式时，由于涉及各个方面的主体利益，所以很难用单一的方法正确测定其不同的运作方式。本文引入信息熵法和G1法，求解指标权重，并使用GRA-VIKOR法对轨道交通PPP项目的运作方式进行排序，以确定项目运作方式的最佳选择。

3.2.1 组合赋权

指标权重赋权方法通常分为主观赋权法和客观赋权法两大类。主观赋权法主要是由相关领域专家根据自身的知识和经验对指标权重的相对重要性作出主观的判断，注重专家经验，但缺乏客观数据支撑；而客观赋权法依托客观数据，经过科学的推导和计算来获得指标权重，具备较强的理论基础，但又存在缺乏专家经验判断的弊端。为获得更科学、合理的指标权重，方案决策和评估等领域更倾向于主客观组合赋权的方法来确定指标的权重。因此，本文选用基于博弈论思想的G1法和熵权法来确定城市轨道交通PPP项目运作方式评价指标的权重。

1) 通过G1法计算主观权重。G1法能全面展现出专家方面的主观意见，并且重要性方面并不伴随指标变动而出现变化的情况，步骤如下：

第一步，指标排序：假设n个指标构成指标集C={C1,C2,…,Cn}，若指标Ci(i∈1,2,…,n)相对于指标Ck(k∈1,2,…,n)具有更高的重要性，即Ci>Ck，以此类推，对全部测量指标的重要性完成排序工作。

第二步，确定重要性：经专家评估的方式明确相邻指标Cj以及Cj+1两者的重要性水平，rj=Cj/Cj+1(j=1,2,…,n-1)，随着Cj比Cj+1重要程度的增加，rj取值分别为1.0，1.2，1.4，1.6，1.8。

第三步，相对权重。计算第j项指标权重u′j：

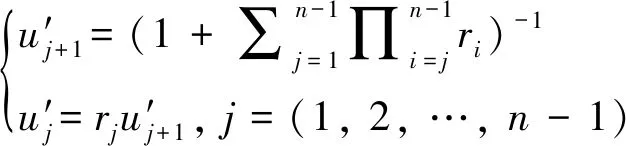
(1)

第四步，计算相对于目标层的指标权重。计算第j项指标权重w′j：

w′j=u′j×u′d

(2)

式中：u′d为第d项准则层的权重值，d=1,2,…,n，其过程与指标层权重的权重解相似。

2) 利用信息熵法计算客观权重。1948年，Shannon首先提出了信息熵的概念，一个系统Y可能出现几种不同的状态y1,y2,…,yn，其中yi(i=1,2,…,n)出现的概率为pi，系统信息熵H(U)如下：

(3)

式中：0≤pi≤1。

步骤如下：

第一步，构建原始矩阵。假设有m个需决策方案，n个衡量指标，则原始矩阵A=(xij)m×n为

(4)

式中：xij为j个指标下i方案的评价值，i= 1,2,…,m；j= 1,2,…,n。

第二步，计算特征比重值pij：

(5)

第三步，计算j指标的熵值Ej：

(6)

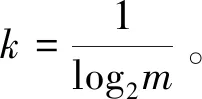
第四步，计算j指标的权重w″j：

(7)

3) 基于G1法与信息熵法相结合的指标权重。确定G1法权重w′j与信息熵法权重w″j在综合权重wj中所占的比重：

wj=v1w′j+v2w″j

(8)

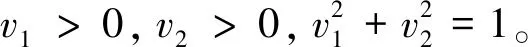
v1，v2的求解可以转化为以下问题：

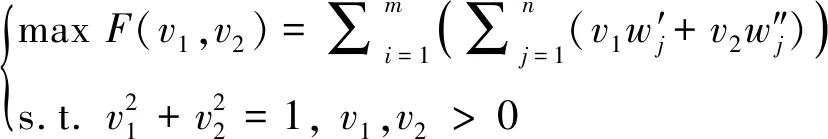
(9)

根据拉格朗日极值条件求解：

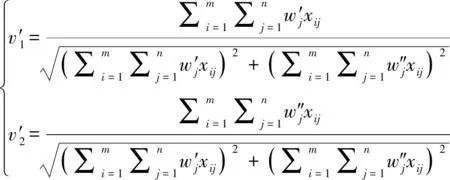
(10)

对v′1，v′2进行归一化处理：

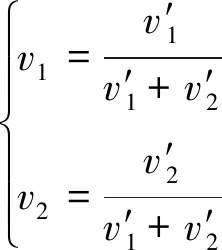
(11)

3.2.2 GRA-VIKOR决策模型

多准则妥协排序法(VIKOR)是针对备选方案存在多个性能评价指标且多个指标间可能存在冲突性的多方案多指标综合优选排序方法。VIKOR法相比TOPSIS等其他优选方法，其选出的方案通常更接近理想方案[17]。但是在信息不完全的情况下，VIKOR法会造成评价不完整，故在该方法中引入灰色关联分析[18-19]，充分挖掘数据信息，使计算结果更准确。

假设有n个决策对象，m个指标，记fij为在指标aj下排序对象Ai的评价值，选择GRA-VIKOR法完成排序分析：

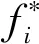
(12)

(13)

式中：I为效益型指标集合；O为成本型指标集合。

2) 计算得到基于传统VIKOR法的群体效益值Si以及个别遗憾值Ri：

(14)

(15)

式中：Si和Ri都属于越小越好的分析指标。

3) 计算最大、最小群体效益值及个别遗憾值：

(16)

(17)

4) 明确方案及其正、负理想解的灰色关联度。在指标aj下，Ai与正理想解的灰色关联系数为

(18)

式中:分辨系数ρ取0.5。

在指标aj下，Ai与负理想解的灰色关联系数为

(19)

式中:分辨系数ρ取0.5。

与正、负理想方案的关联度分别为

(20)

(21)

5) 正、负理想方案相对关联最大指标的关联度：

(22)

式中：αi表征群体效益值；βi表征个别遗憾值。

6) 明确αi及βi最值：

(23)

7) 计算各方案综合指标Qi：

(24)

式中：λi=Si×αi为群体效益值；λ*=S*×α*为群体效益值的最大值；λ-=S-×α-为群体效益值的最小值；μi=Ri×βi为个别遗憾值；μ*=R*×β*为个别遗憾值的最大值；μ-=R-×β-为个别遗憾值的最小值；v为决策偏好系数，该值等于0.5，表征方案选取倾向是折衷态度；超出0.5，则明确倾向是群体效益高；不足0.5，则明确倾向是个别遗憾值低。

8) 明确备选方案排序及其折衷方案。按照λi，μi，Qi升序排列，靠前为优。在满足下列①②的基础上，按升序排列Qi，第一个方案作为最佳解决方案。如果②不满足，A1，A2都是折中方案。如果只满足②的话，不满足①的方案的整体评价最合适。

①Q(A2)-Q(A1)≥DQ，DQ=1/(n-1)；

②A1是λi或μi的排在前面的对象。

4 实证分析

2020年，我国已有超40个城市开通了轨道交通[1]。这些项目在规模、地域、复杂度等方面有差异，但运作逻辑基本一致。本文以昆明市地铁4号线为例，该项目总投资约220亿元，项目具体操作模式如图2所示。结合昆明市的特点，选择BOO，DB，BDO，BOT，PFI，TOT，BOOT和ET这8种运作方式进行研究。

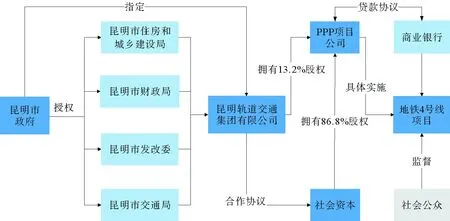
图2 昆明市地铁4号线的具体操作模式

4.1 计算指标权重

根据3.2.1节组合赋权公式计算权重，结果见表3。

表3 昆明市地铁4号线运作方式决策指标权重

4.2 应用GRA-VIKOR法进行排序

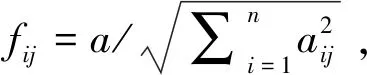
2) 由式(12)(13)确定正、负理想解：

3) 由式(18)—(21)可得：

ε*=(0.696,0.721,0.676,0.610,0.779,0.865,0.857,0.634)，

ε-=(0.655,0.701,0.769,0.801,0.639,0.554,0.563,0.759)。

经式(14)—(17)，能够获得基于传统VIKOR法有关的群体效益值Si、个别遗憾值Ri；经式(22)(23)计算得到基于GRA-VIKOR法的群体效益值αi，个别遗憾值βi，见表4。

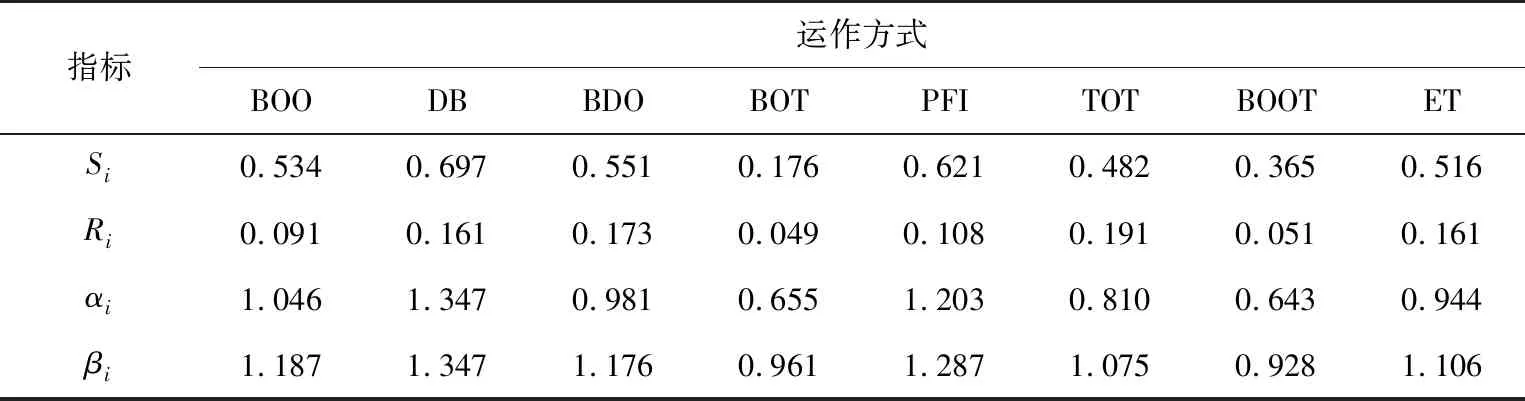
表4 群体效益值和个别遗憾值

4) 由表4数据计算可得λ*=S*×α*=0.113，λ-=S-×α-=0.939，μ*=R*×β*=0.045，μ-=R-×β-=0.257。经由式(24)，能够获得基于GRA-VIKOR法有关的群体效益值λi、个别遗憾值μi以及综合指数Qi，见表5。

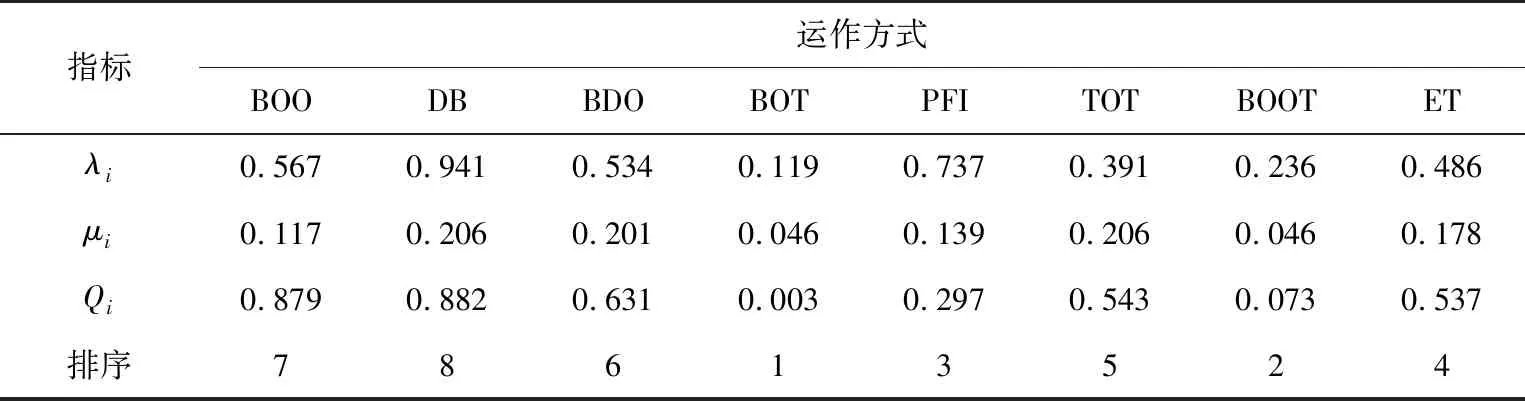
表5 基于GRA-VIKOR法计算结果

考虑到评价对象是PPP项目的8种运作方式，n=8，由此明确DQ=1/(n-1) = 0.143。

参照表4计算所得，将8种运作方式的基于传统VIKOR的群体效益值Si、个别遗憾值Ri以及基于GRA-VIKOR的群体效益值αi、个别遗憾值βi进行对比，可以看出，相对于传统的VIKOR法，GRA-VIKOR法对于区分运作方式差异的灵敏度更高。

参照表5计算所得及其折衷方案判断标准完成排序事项，可得运作方式排名，即BOT>BOOT>PFI>ET>TOT>BDO>BOO>DB。故而，本项目契合度最高的运作方式就是BOT，其次是BOOT，PFI。而云南省昆明市地铁4号线PPP项目正是采用了BOT运作方式，该结果符合实际情况。

5 数据分析

5.1 稳定性分析

在采用GRA-VIKOR法计算过程中，vi系数的取值会影响计算结果。在同时考虑利益最大化和个人遗憾最小化的前提下，为了判断其他条件是否影响评价结果，以0.1为间隔进行11次评价，得到11组不同的综合评价值，见表6。

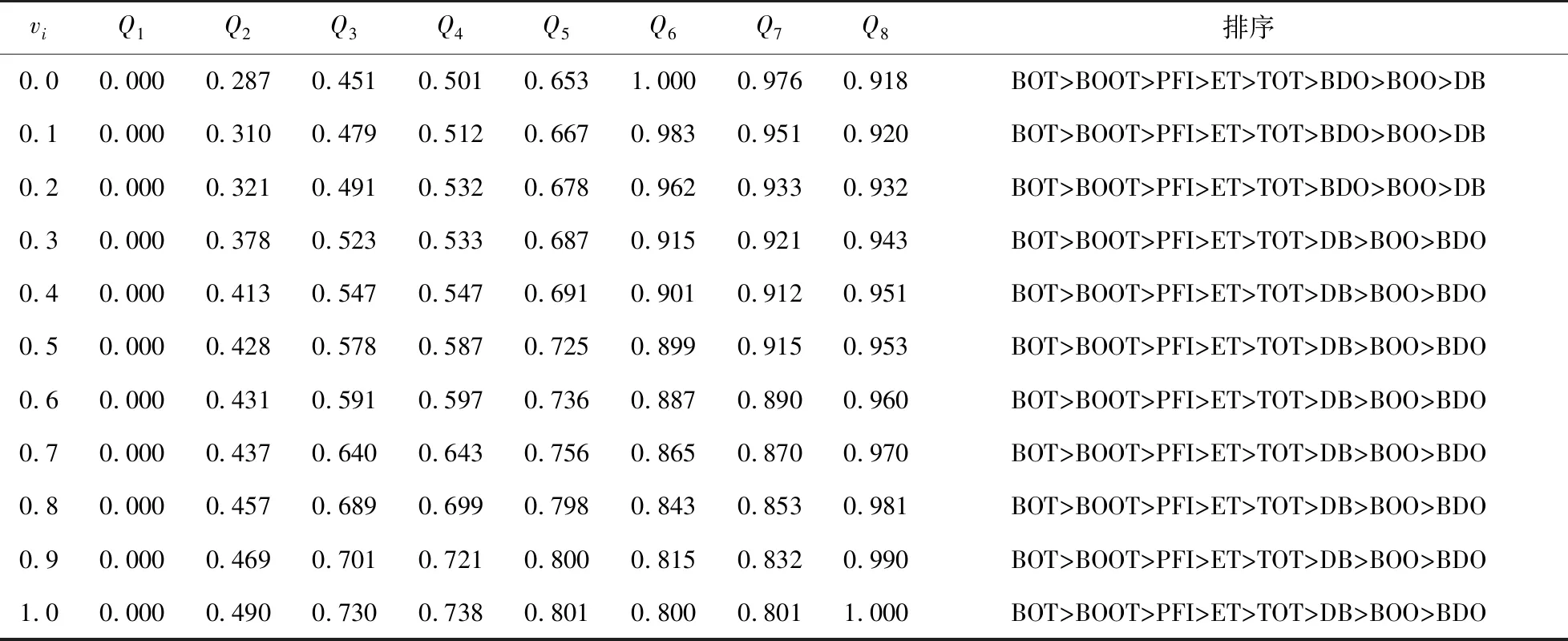
表6 不同 vi值的综合评价值排序

由表6可知，备选方案的排名变化较小。当vi取值范围在[0,0.2]时，排名为BOT>BOOT>PFI>ET>TOT>BDO>BOO>DB，决策者几乎只考虑个别的后悔值，而没有考虑群体的利益。当vi值在[0.3,1.0]时，决策者考虑更多的是群体利益，个别遗憾逐渐减少，得到的排名为BOT>BOOT>PFI>ET>TOT>DB>BOO>BDO。计算只产生了两种排名结果，主要体现在DB和BDO排名结果的差异上。因此，GRA-VIKOR法对扰动不敏感，具有良好的稳定性。

5.2 可信度分析

目前，PPP项目运作方式选择的定量方法主要有改进的TOPSIS (QFD-TOPSIS，GRA-TOPSIS)和蒙特卡罗法，将本文提出的方法与上述方法进行比较，结果见表7。

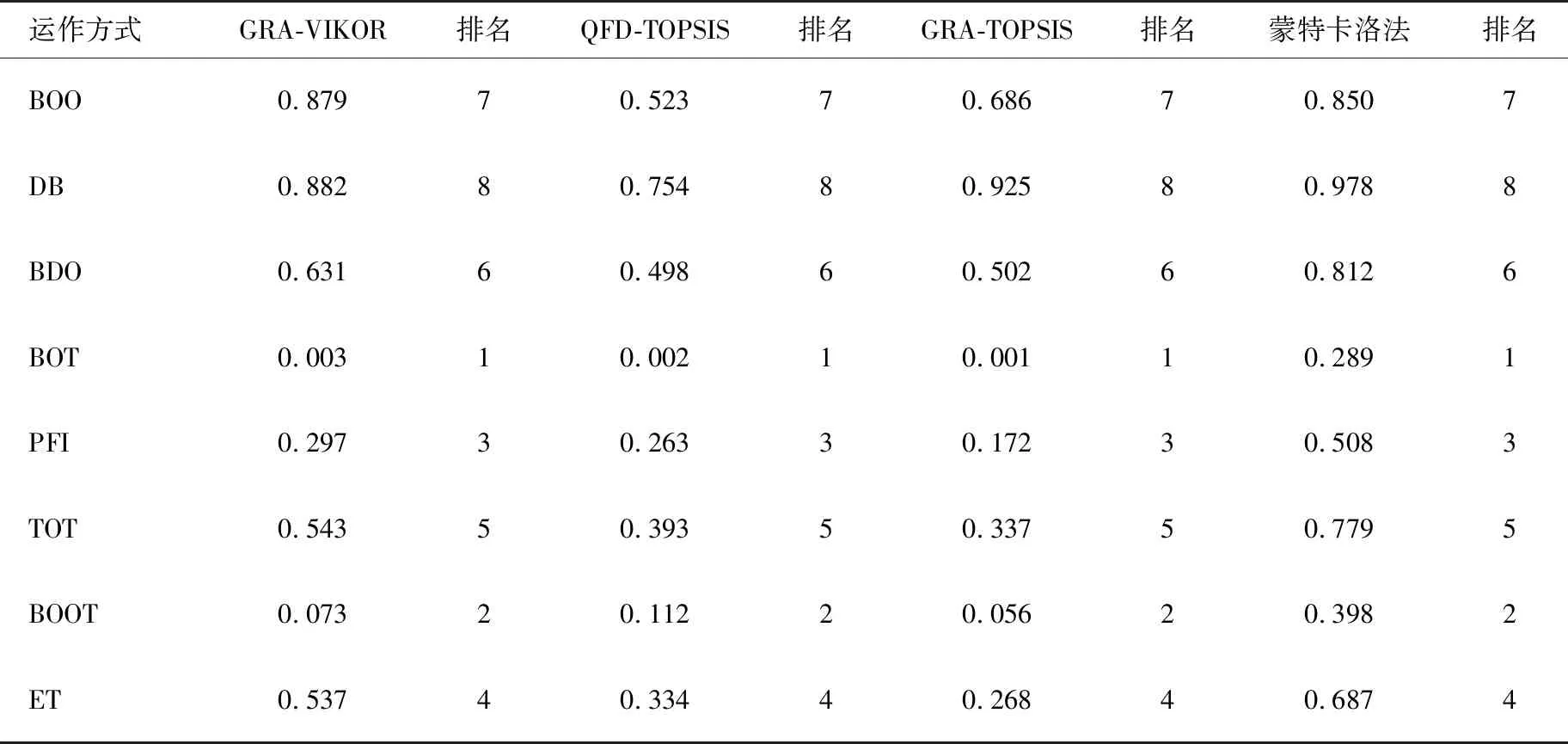
表7 不同方法下的运作方式排名

由表7可以看出，在不同方法中，运作方式的排名结果趋于一致，表明本文提出的评价方法能够获得满意的结果。虽然QFD-TOPSIS克服了数据模糊的问题，但排序是由相对接近系数决定的。使用本文的方法，最优方案总是最接近理想的解决方案。GRA-TOPSIS解决了“不总是最接近理想方案”的问题，但没有考虑到评价数据的模糊性和决策者的态度，因此评价过程会与实际情况不一致。蒙特卡罗方法的结果主要集中在群体效用的最大化上。本文的评价方法强调的是群体综合效用最大化和个别遗憾最小化，它属于折衷方案。因此，与其他三种方法相比，GRA-VIKOR法在备选方案较多的情况下具有更大的优势和可信度。