基于减压阀和供水泵站统一管控管网压力优化技术研究

种宇飞，李红卫,*，尹淑银，吕 谋，岳宏宇

(1.青岛理工大学 环境与市政工程学院，青岛 266525；2.青岛市生态环境局胶州分局，青岛 266300)

供水管网的漏损问题已成为供水行业关注的热点[1]，目前大多供水公司还在利用传统经验控制管理管网的漏损，这虽然能产生一定的作用，但与发达国家相比，漏损控制效果还有较大差距。随着城市管网的老化，供水管网的压力更突出地影响了管网漏损量与爆管发生概率，因此管网压力管控对社会生活、生产意义重大[2]。

当今，多数供水企业仍然采用输水泵站以某一不变压力24 h不间断输配水的旧模式保证用户任意时段的用水需求，但这也使得非用水高峰期整个管网压力维持在较高水平。即便通过改变用水低峰期水泵站的输送压力和水量，也会导致在很多时段管网局部压力大大超出该地区所需最小服务水头。管网压力偏高造成能耗浪费，导致企业运行成本、用户用水成本增加，管路阀件损坏，这样的管理模式偏离建立“智慧水务”的初衷。

针对上述问题，国内外研究者进行了大量的探索并取得了一定性的进展。CANDELIERI 等[3]提出了采用动态拓扑结构管网建立水泵调度模型，较好模拟了管网运行工况。XU等[4]提出了在线控制减压阀的开启程度，优化整个管网剩余压力的方法。PAOLA等[5]采用和声搜索算法论述了供水管网减压阀设定值的相关理论。牟天蔚等[6]通过卷积神经网络建立了压力预测模型，通过模型求解优化水泵参数调度。黄茂林[7]、王磊[8]进行压力控制算法的研究，论述了压力控制管网漏失的相关理论，应用遗传算法找准了减压阀在管网中设置的位置、个数以及开启度。游庆元等[9]利用SCADA系统数据建立了寻求泵房出水流量使压力最优的数学模型，采用混合遗传算法求解该模型，使整个管网压力趋于均衡来降低漏损。

上述研究采用对水泵进行开关或减压阀位置、个数的设定等方式，仅从单一方面影响了管网的运行工况，一定程度上控制了管网的漏损量，但无法更精细化地管理全部管路。本文综合考虑管网中各管路、水泵的水力特性，采用减压阀和供水泵站统一管控管网压力的方式使选定的水泵一直处在高效率运行工况区间，结合调节减压阀的阀后压力，以实现各节点的自由水压趋近该节点所需最小服务水头，从全局实现更高效的科学管理和漏失控制。

1 阀门协同泵站调控压力模型

管网压力的变化在管网前端主要是通过对送水泵站变速泵转速的改变来实现对送水扬程的调控，在管网中段主要是通过增减阀门的数量、设定的位置以及阀门的开启程度来改变管网水压。为了更好地控制压力、减少漏失，笔者期望找到最优的变速泵转速比和减压阀的阀后压力设置值，故建立阀门协同泵站调控压力模型，通过模型的处理实现阀门与泵站的最优协同。

1.1 变速泵转速比与管网压力的确定

变速泵通过变化转速的大小来改变出水口压力的大小。水泵性能参数之间的关系用水泵特性曲线表示，在水泵特性曲线上，对应任意流量点都可以找到1组与其相对应的参数称为工况，其对应最高效率点的1组工况称为最佳工况。在生产实践中，水泵的运行工况点是通过管路的特性曲线与水泵的特性曲线确定的。在选择和使用泵时，使水泵在高效区运行，以保证运转的经济和安全，一般变速泵满足在高效率运行工况时的区间转速与提供最大压力时的转速之比：0.6≤nb≤1[10]。

1.2 目标函数的确定

节点自由水压与最小服务压力之差的平方和可以很好地反映整个管网压力的均匀程度，故可采用节点自由水压与最小服务压力之差的平方和作为目标函数。目标函数的运算结果可用数字和图像的形式直观表达，便于了解整个管网压力的变化过程并最终确定各节点压力达到最经济状态。目标函数的表达式为

(1)

式中：ΔP为管网相对于最小服务压力的剩余压力的平方和；Pi为节点自由水压，MPa；Pmin为最小服务水头，MPa；N为供水管网中节点数。

1.3 约束条件的确定

压力驱动节点流量方程是对连续性方程和能量方程的综合利用，是一切管网正常运转的前提条件，被广泛应用在现实生活当中。本研究还需设定各节点自由水压始终不小于该点最小服务水头以及转速比始终满足水泵在高效区运转等为约束条件，故设置以下约束条件：

1) 压力驱动节点流量方程：

(2)

式中：Hd为节点临界压力，MPa；Hmin为节点最小供水水头，MPa；Ni为与i相连的节点；Pj为节点j的自由水压，MPa；m为压力指数；sij为摩阻系数；Qi-d为节点额定用水量；ki为节点漏失系数；n为漏失指数，其范围为0.5～2.5，本文取普遍认可的结果1.18[11]；hij为水头损失。

2) 节点压力：

Pi≥Pmin

(3)

3) 变速泵转速比：

0.6≤nb≤1

(4)

4) 减压阀阀后压力：

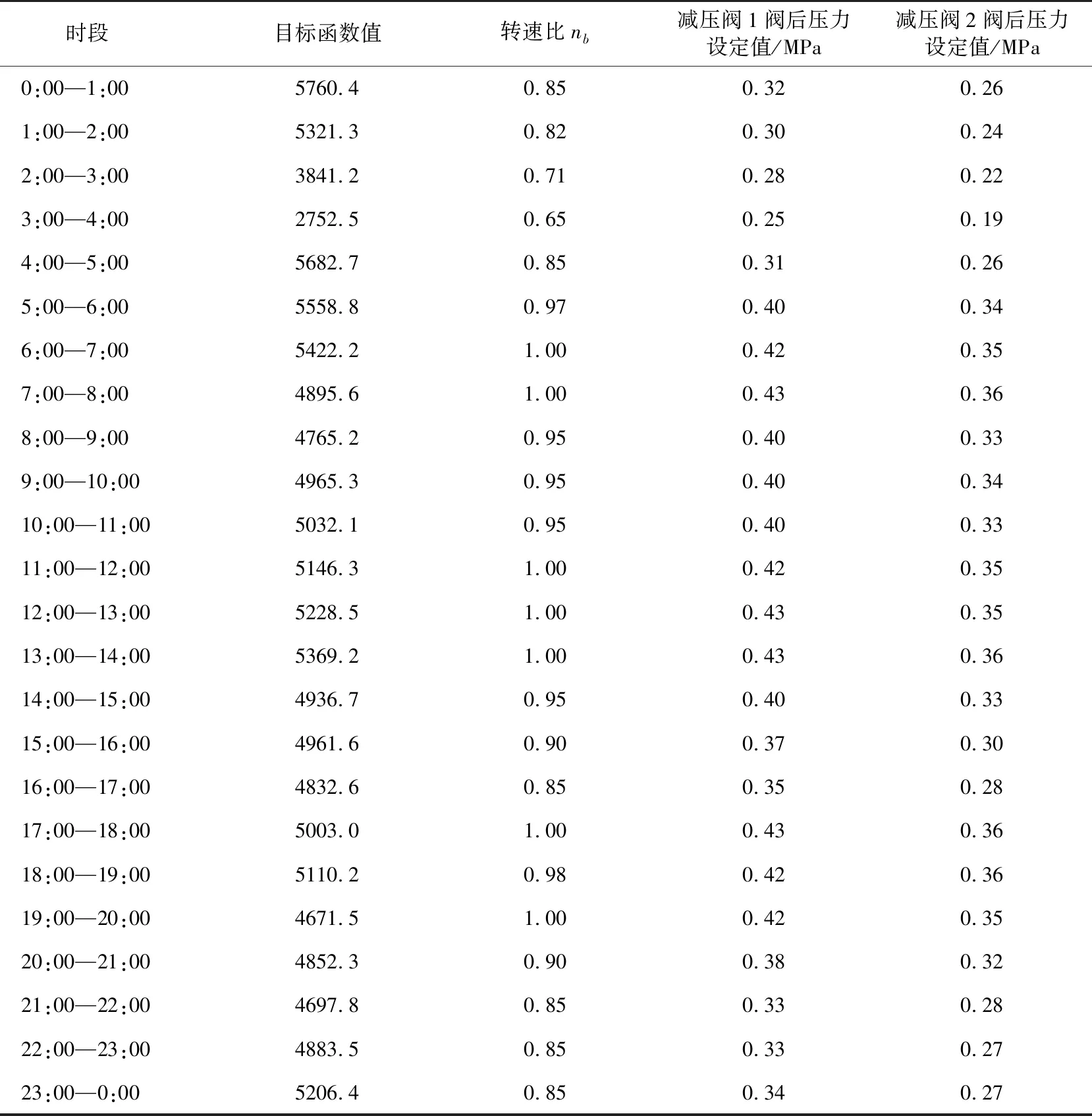
Pmin

(5)

式中：X为减压阀阀后压力值；Xb为减压阀阀前压力值。

2 模型求解

2.1 粒子群算法简介

粒子群算法(Particle Swarm Optimization)是EBERHART和KENNEDY在1995年提出的一种基于种群的进化计算技术[12]，在算法中把一个优化问题看作是在空中觅食的鸟群，获取的“食物”就是优化问题的最优解，空中飞行的每一只觅食的“鸟”就是该算法在解空间中进行搜索的一个“粒子”，表示为xi=(x1,x2,…,xn)，速度为vi=(v1,v2,…,vn)，适应度值为Fit[i]。空间中每个粒子都具有当前位置、当前速度、当前位置与自己最好位置之间的距离(个体极值pbest)、当前位置与群体最好位置之间的距离(gbest)。粒子的更新公式为

V[]=ωV[]+C1rand()(pbest[]-present[])+C2rand()(gbest-present[])

(6)

present[]=present[]+V[]

(7)

图1 模型求解过程

式中：V[]为粒子的速度；ω为惯性权重；present为粒子当前位置；rand为(0，1)之间随机数；C1，C2为学习因子，C1=C2=2。

2.2 基于粒子群算法的模型求解

粒子群算法处理模型数据的具体过程见图1。

3 案例分析

选取东南沿海某城镇管网作为研究对象，该区域目前有2座水厂，供水能力共7.5万m3/d，目前可以满足全城镇生产生活用水。该城镇可以分为三大区域，选取其中1个代表性区域建立模型，其管网拓扑结构如图2所示，通过1座水池和4个水泵组成的机组来表示水厂向该地区管网供水，39个节点，45条管段，2个减压阀。4个水泵的基本参数如表1所示，泵站的最高输出压力不会超出0.5 MPa，故不考虑压力过高爆管的情况。依据该地区最不利点的压力需求及该区域内建筑的层高，最小服务水头在每日的5：00—24：00时取0.25 MPa，0：00— 5：00时取0.15 MPa。

图2 东南沿海某城镇管网

表1 水泵基本参数

3.1 减压阀位置的确定

对减压阀进行定位时，发现由于区域分区计量(DMA)之后每个小区的压力变化具有极大程度的相似性，同时也具有一定范围的可调值，故可以将减压阀安装在每个分区的入口处，以实现各分区压力的独立控制，故本模型选用2个减压阀。

3.2 用水节点的漏失系数ki的确定

英国水研究中心(WRC)经过长时间统计并分析夜间2：00—4：00的人均用水量数据，提出夜间人均用水量为1.7 L/(户·h)。以此为基础，可以较好地推算一个地区夜间最小流量时刻的管网漏失量。

通过收集到的算例管网信息可知，该地区夜间最小流量为40 m3/h，用户数为2932户，可推算出该地区夜间最小流量时刻的管网漏失量为35 m3/h。

q(tmin)=Q(tmin)-0.0017×用户数=40-0.0017×2932=35(m3/h)

式中：q(tmin)为区域夜间最小流量，m3/h；Q(tmin)为区域夜间最小流量时刻的管网漏失量，m3/h。

该地区夜间最小流量时刻的各节点流量与压力由EPANET软件运行可得，见表2。

表2 夜间最小流量时刻各节点流量与压力值

式中：di(tmin)为夜间最小流量时刻各节点的流量值，L/s；pi(tmin)为夜间最小流量时刻各节点的压力值，MPa；Id为区域内所有节点。

引入比例因子作为漏失系数与流量的比值，可得比例因子和各节点漏失系数ki：

ki=β·di(tmin)

式中：β为比例因子。

得到各用水节点的漏失系数值ki(表3)。

表3 各用水节点的漏失系数ki值

3.3 求解模型

3.3.1 求解模型整体思路

1) 将随机产生的转速比和阀后压力设定值代入EPANET软件，得到各节点的自由水压值，结合本地区最小夜间流量求得漏失系数的比例因子；

2) 由比例因子求得管网各节点漏失系数；

3) 将确定好的各参数值结合粒子群算法对阀门协同泵站调控的压力模型进行求解；

4) 全天24 h设置24个工况，对每个工况进行求解寻优，得到变速泵最优转速比和减压阀最优阀后压力设置值；

5) 将最优转速比和减压阀最优阀后压力设置值代回EPANET软件，得到24组优化后节点自由水压值；

6) 采用式(8)计算优化后整个管网的漏失水量：

(8)

式中：Qleak为漏失水量；ki为节点i的漏失系数；Hi为节点i的压力；n为漏失指数。

3.3.2 模型求解结果

最终模型求解结果如表4所示。

表4 计算结果

24个工况在算法求解后会得到24组变速泵最优转速比和减压阀最优阀后设置值，分别将这些值重新代入EPANET软件中即得到全天每个时段各个节点的自由水压值，然后将这些自由水压值代入式(8)中便能得到通过优化后整个管网的漏失量。

算例供水管网供水总量为2820.3 m3/d，分区前管网的漏失水量为477.8 m3/d，该模型优化后的漏失水量变为312.4 m3/d，供水管网漏失率从16.94%降低为11.08%，降低了5.86%。该方法采用智能优化算法，从全局实现更高效的科学管理和漏失控制，为“智慧水务”的发展提供了技术支撑。

4 结论

本文针对国内现有的对供水管网压力控制模型及智能优化算法研究的不足，为了更有效管理供水管网压力，减少管网漏失率，利用变速泵转速变化引起管网中压力变化的原理，建立新的阀门协同泵站调控压力模型，以达到管网压力最小化，各节点压力趋近最小服务水头的目的。经实例验证，该方法可行且优化效果显著。

1) 模拟东南沿海某城镇管网建立管网模型以及数学模型，利用粒子群算法在限定条件下对目标函数进行寻优，最终确定24个工况下24组变速泵最优转速比和减压阀最优阀后设置值。采用EPANET软件对求解结果在模型中重新模拟水力计算，两者互相配合，为智能算法在控制管网漏失方面提供理论支持。

2) 从目标函数的寻优结果来看，阀门协同供水泵站统一管控的一体化调控方案使算例管网压力的布局更加科学、合理，漏损量也大大降低，推广到整个管网对供水企业意义重大。

3) 管网优化目标多种多样并且相互干扰，本研究利用控制变量法仅考虑1个目标函数，未来解决管网优化问题的方向必然是多目标优化设计，需要在此基础上不断努力以期更好地解决管网漏失问题。