基于扩展有限元的空洞影响下隧道结构裂损机制研究
2023-01-06陈耀鹏李文华陈德刚张素磊
陈耀鹏,李文华,刘 昌,陈德刚,周 明,张素磊,,*
(1.青岛理工大学 土木工程学院,青岛 266525;2.青岛海川建设集团有限公司,青岛266032;3.北京交通大学 城市地下工程教育部重点实验室,北京100044;4.青建集团股份公司,青岛266071;5.慈溪市交通建设工程质量安全监督站,宁波 315300)
截止到2020年年底,我国已建公路隧道21 316座,总里程2 199.93万m[1]。随着隧道运营时间的增加,隧道病害问题日益突出,而衬砌背后空洞的存在对隧道的影响较大,改变了衬砌结构的受力特性,最终致使衬砌开裂现象的发生[2]。朱旺等[3]通过地质雷达无损检测的方法,发现衬砌背后存在空洞情况较多;此外,应国刚[4]结合120余座铁路隧道和公路隧道的检测数据,系统性地分析了隧道衬砌背后空洞对衬砌结构的致害机理;MEGUID Mohanmed[5-6]不仅对空洞进行成因分析,同时还研究了空洞对衬砌轴力和弯矩的影响;鲍彤等[7]依托三维数值模型,对衬砌结构内力及安全性变化规律进行分析;MIN Bo等[8]基于三维有限元模型,发现隧道衬砌背后局部空隙会造成附近的土压力重分布,从而改变隧道衬砌开裂的原有机理;YASUDA Naotoshi等[9-10]使用子结构法和点匹配法得出衬砌背后空洞条件下应力状态从受压转变为受拉;XIN Chunlei等[11]通过对比在相同扰动下有无空洞的隧道,分析得出各自的损伤模式;GAO Yang等[12]将围岩和衬砌混凝土之间的不连续接触简化,并采用加速度波测量方法得出衬砌结构的应力状态取决于衬砌背后空洞尺寸和空洞位置;蔡义等[13]借助有限差分软件和室内试验,分析了不同空洞位置对地铁隧道施工过程的影响;张成平等[14-15]基于模型试验,对拱顶和拱肩存在双空洞条件影响下的隧道结构受力状态进行了研究;黄宏伟、张芳等[16-17]针对浙江地区众多隧道,采用荷载-结构模型分析了衬砌背后空洞存在条件下裂缝产生和发展的过程;车增军[18]结合隧道衬砌病害统计数据,分析得到直墙式隧道拱部空洞环向范围在达到一定值后,衬砌才会发生开裂;闵博、张旭等[19-20]通过数值模拟分析对比了在有无空洞存在条件下非对称连拱隧道结构的裂损情况;LIU Chang等[21]为了解衬砌损坏的隧道结构的运行状态,通过现场调查、数值分析和原位监测,对山区隧道衬砌损坏的特点和处理措施进行了案例研究;刘昌等[22]针对围岩流变中隧道衬砌的损坏状况,建立了时效解析模型,并通过数值分析验证了模型的准确性。综上分析,已有大量学者对衬砌背后空洞这一现象进行了研究,但是针对衬砌背后不同位置、不同大小空洞下衬砌裂损全过程演化过程的研究较少,为深入了解空洞条件下衬砌裂损机制,本文结合100余座公路隧道衬砌背后空洞实际服役状况,基于扩展有限元法建立空洞计算模型,以获取衬砌背后空洞条件下衬砌裂损机制及演化过程,最终为我国公路隧道衬砌结构病害预防和修复提供参考。
1 衬砌背后空洞分布状况

图1 衬砌脱落事故孕育过程
近年来由于衬砌脱落造成的安全事故屡见不鲜,例如,2016年的济南开元隧道以及2020年的四川青鼻山隧道在拱顶处都发生了衬砌混凝土脱落的现象[18],造成了一定的人员伤亡。通过分析不难发现衬砌背后空洞是衬砌脱落的主要成因之一,并且对隧道运营也存在着巨大的安全隐患,空洞主要是由施工过程中工人操作不当造成的,在不良地质条件及荷载变异作用下空洞的存在恶化了围岩-支护作用关系,导致衬砌开裂、破损,最终出现衬砌脱落等安全事故,图1为空洞存在条件下衬砌脱落事故孕育过程。
结合100余座公路隧道衬砌无损检测资料,对所检测的1117处空洞所处位置、围岩级别进行统计分析,现场检测及雷达处理图像见图2。

图2 现场检测及雷达处理

图3 空洞分布情况统计

表1 不同围岩条件下脱空分布密度

图4 模型示意
空洞按所处围岩级别及分布位置分类统计如图3所示。
为更好地对比不同围岩级别下衬砌背后脱空出现的相关情况,对所检隧道空洞出现的次数以及不同围岩级别的长度进行了统计分析,结果见表1。
综合可见,空洞主要分布于IV级及V级围岩,并且由于重力作用,边墙背后的空洞数量明显少于拱部。
2 数值模型建立
依托某双向两车道隧道工程,结合现场衬砌背后空洞检测数据,基于扩展有限元(XFEM)方法采用ABAQUS有限元计算软件建立二维地层-结构模型,以研究存在空洞时衬砌结构的裂损机理。该隧道实际净高9.5 m、净宽11.6 m,二维计算模型长×高为120 m×55 m,拱顶埋深为20 m,模型底部限制竖向位移,左右边界限制水平位移。为模拟不同埋深条件,在模型顶部施加均布荷载,最大荷载为3 MPa,计算模型见图4。


表2 材料力学参数
通过现场检测结果可知,95%的空洞分布于拱部,因此,本文分别就拱顶、拱腰背后空洞条件下衬砌结构破损机制进行研究,而空洞环向范围(图4中θ)分别设为10°,20°,30°及40°,空洞形状假设为环形,空洞高度设为0.5 m,空洞与隧道相互位置关系见图4。
3 空洞条件下衬砌裂损机制

图5 无空洞条件下衬砌最小主应变云图
将无空洞工况下的计算结果作为分析空洞影响下衬砌结构裂损规律的基础数据,需要补充说明得是,本文仅对裂缝扩展至贯通前的衬砌裂损机制进行分析。衬砌背后无空洞时的裂损情况如图5所示,衬砌施作后,在两侧拱脚出现拉应力集中现象,在外侧各出现一条裂缝,由于围岩与衬砌结构接触完好,在外荷载的作用下,衬砌除拱脚外主要以受压为主。施加荷载过程中,拱脚内侧压应力集中现象明显,最小主应变的最大值为0.0027,但小于混凝土结构的极限压应变,未出现压溃现象。
3.1 拱顶背后空洞影响下衬砌裂损机制
3.1.1 衬砌结构裂损演化过程
与无空洞工况下一样,拱顶背后空洞影响下衬砌结构首先在拱脚外侧开裂。当拱顶存在10°,20°空洞范围时,两者裂缝扩展模式基本一致,随着荷载的增加,仰拱外侧拉应力逐渐增大且出现应力集中现象,因此首先在仰拱外侧两边各出现1条裂缝,随着荷载进一步加大,仰拱内侧拉应力范围不断扩大,随之在仰拱内侧两边也各出现1条裂缝;当空洞的环向范围θ=30°,40°时,在荷载作用下衬砌结构拱顶向外变形越来越明显,拱顶外侧结构最大主应力由受压状态转变为受拉状态,且随着荷载的增大拉应力也在不断增大,当拱顶外侧结构超过极限拉应力时则发生开裂,同样,拱顶内侧靠近空洞两侧位置在拉应力作用下也发生开裂,θ=10°,30°时的衬砌裂缝分布见图6(图中数字代表开裂顺序)。

图6 拱顶背后空洞衬砌结构最小主应变云图
为进一步分析衬砌结构裂损机制,对衬砌结构受力特性进行分析。图7为拱顶背后不同环向范围空洞的衬砌结构弯矩,可以看出,当无空洞时拱顶衬砌承受负弯矩,处于内侧受拉状态,且弯矩值较小,而拱脚两侧弯矩值最大,外侧受拉且出现应力集中现象,仰拱部位承受负弯矩,且其数值要大于拱顶和拱腰部位,因此首先在拱脚部位发生开裂现象;随着空洞环向范围的增加,拱顶部位的弯矩值由负值变为正值,拱顶外侧由受压状态转变为受拉状态,且其两侧的负弯矩值也随之增加,当超过其自身的极限拉应力时则发生开裂,因此出现图6中③④裂缝。

图7 拱顶背后不同环向范围空洞的衬砌结构弯矩(单位:kN·m)
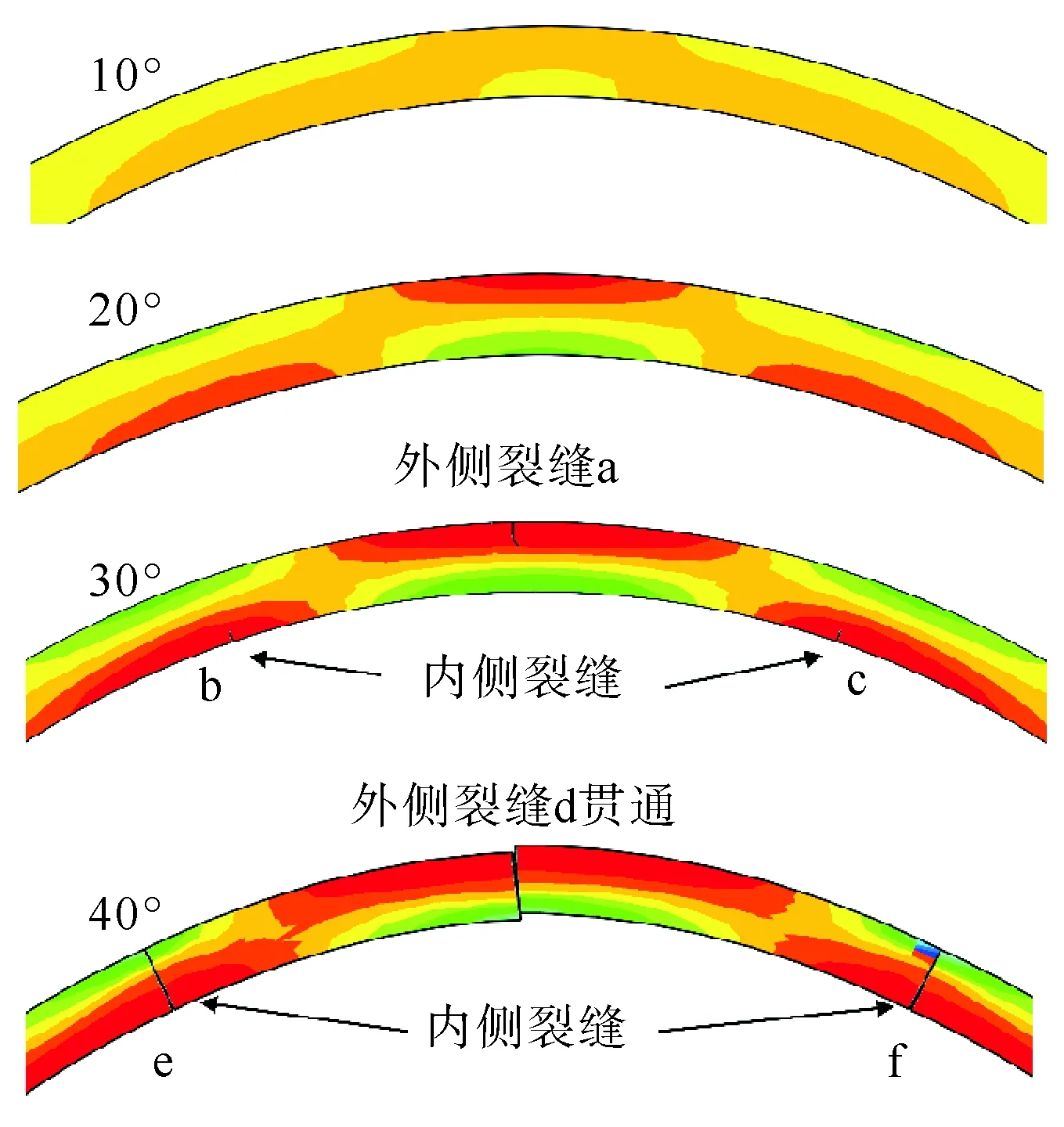
图8 拱顶背后空洞条件下拱部裂缝分布
拱顶背后空洞改变了围岩与衬砌结构间应力传递路径,恶化了衬砌结构力学特性,对拱部衬砌结构的变形及应力影响显著,因此,重点对拱部裂缝扩展进行分析。图8为拱顶背后不同大小空洞条件下拱部裂缝分布,当θ=10°,20°时,拱部存在拉应力集中区域,其拉应力未达到极限值,未开裂。空洞θ=30°时,当荷载达到0.3 MPa时拱顶外侧开裂,荷载达到0.63 MPa时在空洞左、右边界衬砌内侧各出现1条裂缝(裂缝b,c),拱顶外侧裂缝最终扩展深度为13.3 cm。当θ=40°时,衬砌结构受力性能急剧恶化,衬砌施作后拱部即出现开裂(裂缝d,e,f),在加载前期拱部内侧裂缝扩展速度大于拱顶外侧裂缝扩展速度,随着拱腰内侧裂缝的扩展,有效承载面积减小,荷载逐渐向裂缝两侧转移,加上拱顶衬砌持续的“外凸”效应,导致拱顶外侧受拉荷载进一步增大,因此,在加载后期拱顶外侧裂缝d扩展速率显著增大,当荷载为2.56 MPa时拱顶外侧裂缝贯通,此时认为结构失效。可见,拱顶背后空洞越大,拱部衬砌开裂荷载越小,裂缝扩展深度越大,结构承载能力降低越多。
3.1.2 衬砌裂缝扩展规律
拱顶和拱腰裂缝是衬砌背后空洞条件下结构力学特性恶化的结果,裂缝在扩展的过程中将会同时产生错动和张开。图9为空洞θ=30°时拱顶和拱腰裂缝两侧位移变化曲线。可见,裂缝两侧位移均随荷载增大而增大,拱顶裂缝两侧A1,B1的径向位移变化规律基本一致,而环向位移差值逐渐增大,表明裂缝张开度越来越显著;而拱腰内侧裂缝A2,B2的径向位移及环向位移整体变化规律相近。因此,从断裂特征来看,拱顶外侧裂缝为“张开型裂缝”。
图10为空洞θ=40°时拱部裂缝两侧位移变化曲线。加载前期拱顶裂缝两侧A3,B3点位移变化规律与A1,B1相近,当荷载达到2.56 MPa时裂缝贯穿,衬砌结构整体性破坏,B3向空洞临空一侧“外翘”,B3点出现约1.8 mm的径向突变和0.5 mm的环向突变,即裂缝的张开程度及错动幅度均增大,拱顶外侧裂缝则由最初的“张开型裂缝”演变为“复合型裂缝”。

图9 拱顶30°空洞时裂缝两侧位移曲线

图10 拱顶40°空洞时裂缝两侧位移曲线
拱腰A4,B4两点间位移差随着荷载增大呈微弱增大趋势,位移变化规律与θ=30°工况下A2,B2点位移变化规律相同。由于空洞θ=40°时,拱顶“外凸”效应较θ=30°更为显著,抵消了一部分结构在荷载作用下产生的变形,因此,θ=40°时拱部结构的径向位移小于θ=30°时的径向位移。
3.2 拱腰背后空洞影响下衬砌裂损机制
3.2.1 衬砌结构裂损演化过程
与拱顶背后空洞工况一样,拱腰背后空洞存在时,衬砌结构首先在拱脚外侧开裂,当空洞θ=10°,20°时,两者仰拱均在荷载增大至0.26 MPa时开裂;而当θ>20°时,由于左侧拱腰背后空洞的存在改变了仰拱应力分布规律,使得靠近空洞一侧仰拱的内侧拉应力减小,因此,仰拱仅在右侧开裂。当空洞的环向范围θ=30°时,在荷载作用下左拱腰内、外侧开始出现开裂现象。θ=10°,30°时的衬砌裂缝分布见图11。

图11 拱腰背后空洞衬砌结构最小主应变云图
图12为拱腰背后不同环向范围空洞的衬砌结构弯矩,当无空洞和空洞环向范围较小时拱腰衬砌处于外侧受拉状态,但弯矩值较小,衬砌结构最大主应力并未达到混凝土结构开裂值,因此不会产生裂缝,而拱脚两侧弯矩值最大,外侧受拉且出现应力集中现象,仰拱部位承受负弯矩,且其数值要大于拱顶和拱腰部位,因此首先在拱脚部位发生开裂现象;随着空洞环向范围的增加,拱腰部位的弯矩值也不断增大,且两侧的弯矩值也随之增加,当超过自身的极限拉应力时则发生开裂,因此出现图11中③④裂缝;此外,随着空洞环向范围的增加,使得靠近空洞一侧的仰拱弯矩值减小,最大主应力不再超过结构极限拉应力,因此仅在右侧仰拱开裂。

图12 拱腰背后不同环向范围空洞的衬砌结构弯矩(单位:kN·m)
图13为拱腰背后不同环向空洞条件下拱部裂缝分布。当θ=10°,20°时,在衬砌结构的外侧及靠近拱顶方向的内侧出现较明显的拉应力区域,但是均未出现开裂现象。

图13 拱腰背后空洞条件下拱部裂缝分布
随着θ的增大,左侧拱腰局部力学性能进一步恶化。当θ=30°时,荷载增大至0.13 MPa时在左拱腰外侧(空洞中心线处)开裂,荷载达到0.52 MPa后在拱腰内侧(靠近拱顶侧)出现裂缝b,外侧裂缝a最终扩展深度为13.3 cm。对于θ=40°工况,与拱顶背后空洞一样,衬砌施作后即出现裂缝c和裂缝d,当荷载为0.55 MPa时在空洞另一侧(靠近边墙侧)出现裂缝e,当荷载达到1.50 MPa时,拱腰外侧裂缝c贯通,此时裂缝d、裂缝e扩展深度分别为33,20 cm。由上述分析可知,拱顶背后空洞θ=40°时拱顶外侧裂缝贯穿时的荷载为2.56 MPa,因此可得,拱腰背后存在空洞时,衬砌结构承载能力比空洞位于拱顶时的降低41%。
3.2.2 衬砌裂缝扩展规律
图14为拱腰背后空洞θ=30°时裂缝a及裂缝b两侧位移变化曲线。可见,裂缝两侧位移随荷载增大而增大,对于外侧裂缝a而言,当荷载大于0.5 MPa后,径向位移增大速率逐渐减缓,此时拱腰内侧开始开裂,表明内侧裂缝b与外侧裂缝a扩展存在一定的内在联系;随荷载增大,裂缝a两侧A1,B1及裂缝b两侧A2,B2的径向位移差值变大,而环向位移差值增大幅度不明显,因此,从裂缝扩展模式来看,裂缝a为“滑开型裂缝”。与拱顶背后θ=30°空洞相比,拱腰背后空洞工况下外侧裂缝的径向位移小于前者,但环向位移远大于前者。
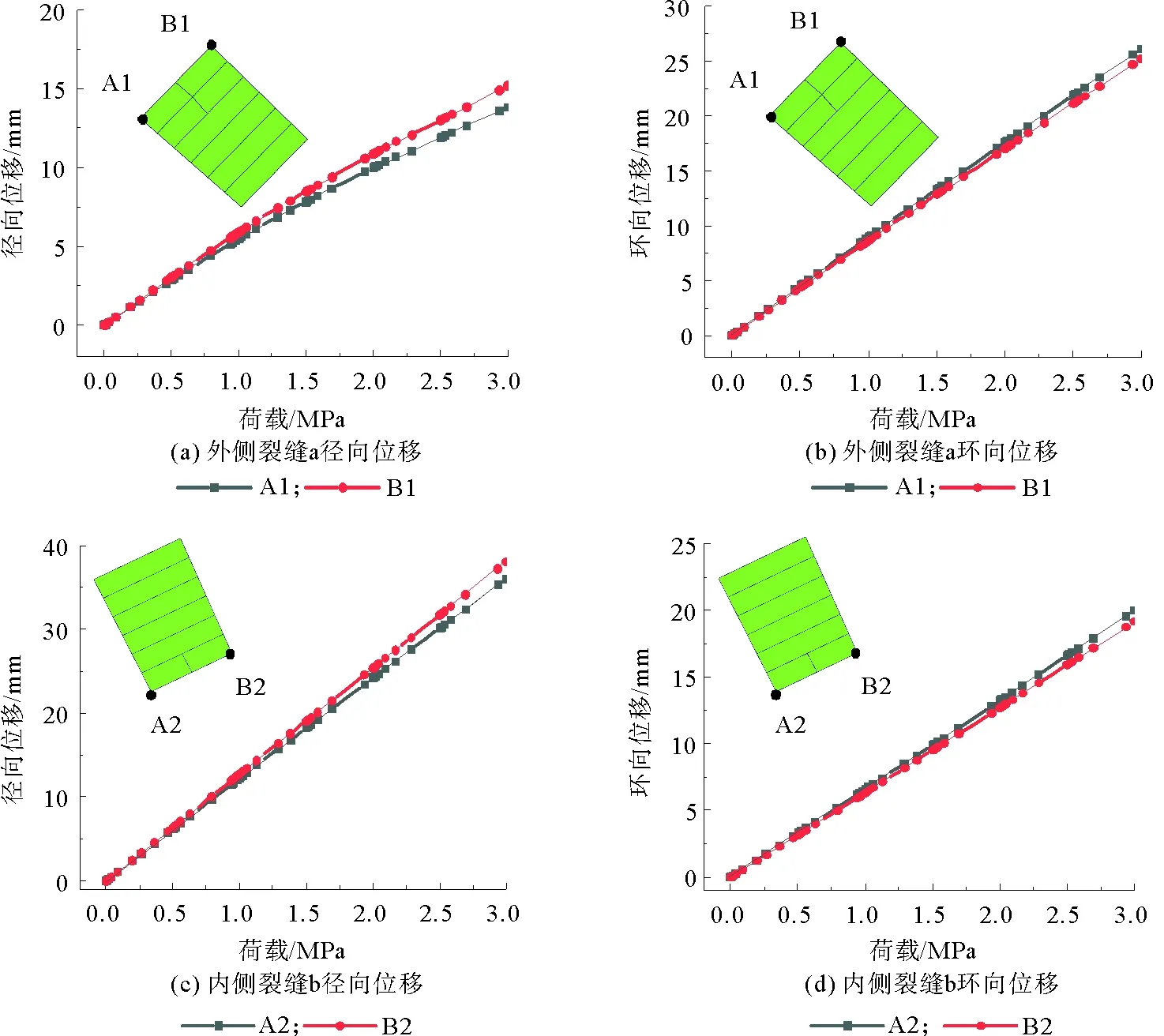
图14 拱腰30°空洞时裂缝两侧位移曲线
图15为空洞θ=40°时裂缝c及裂缝d两侧位移变化曲线。与θ=30°相比,θ=40°时裂缝两侧位移值存在不同幅度的减小,由于空洞范围内衬砌结构局部的“外凸”现象,拱腰外侧裂缝c径向位移增大速率随荷载增大而减小,并且当荷载增至1.50 MPa时,裂缝c贯穿,此时A3,B3同时“外翘”,因此两者径向位移存在约1 mm的突变,而环向位移基本呈线性增大,此时可认为裂缝c为“滑开型裂缝”。裂缝d两侧A4,B4位移呈线性增大趋势,两者径向位移差值在加载后期逐渐增大,裂缝d两侧错动幅度也越来越大;此外,由于θ=40°时的“外凸”效应要强于θ=30°,因此,θ=40°时拱部结构的径向位移小于θ=30°时的径向位移。

图15 拱腰40°空洞时裂缝两侧位移曲线
4 结论
1) 结合100余座公路隧道衬砌无损检测资料,对所检测的1117处空洞所处位置、围岩级别进行统计分析,得到衬砌背后空洞分布的普遍规律。
2) 无论是否存在空洞,衬砌均在拱脚外侧拉应力集中区域率先开裂,衬砌背后存在空洞时,仰拱结构两侧开始出现裂缝,当拱顶空洞环向范围θ达到30°时,拱顶外侧开始出现裂缝,接着在衬砌内侧开裂。当拱腰背后空洞存在时,对拱顶一侧衬砌力学性能恶化程度较临近边墙一侧的衬砌结构严重;同时,拱腰背后空洞的存在改变了仰拱应力分布规律,使得靠近空洞一侧仰拱拉应力减小,仰拱仅在远离空洞一侧开裂。
3) 空洞环向范围越大,拱部衬砌开裂荷载越小,裂缝扩展深度越大,结构承载能力降低幅度越大,其中,拱腰背后空洞对衬砌结构承载能力降低幅度大于拱顶背后空洞。
4) 随着空洞环向范围的增大,拱部结构首先在外侧开裂(约空洞环向范围轴线处),并且结构最终沿此条裂缝扩展至贯穿,而裂缝扩展模式受荷载及空洞环向范围影响显著,此点应引起足够重视。
