侧面碰撞子结构模型精度的参数研究

刘正午，郝琪，梅佳炜，王兴东，田立胜

（1.湖北汽车工业学院汽车工程学院，湖北十堰 442002;2.东风（十堰）车身部件有限公司，湖北十堰 442002）

碰撞模拟作为实现汽车安全性和功能性设计目标的有效手段，一次计算往往需要经过上千次迭代。通常使用模型降阶的方法减少整车模型的自由度，达到缩减计算量的目的。［1-2］模型降阶的基本思想是对大型动力系统进行近似处理，即用很小的n维系统来替代N维有限元模型的非线性常微分方程系统。［3-4］大型动力系统的输入、输出以及稳定性等特征应尽可能精确地保留在小型n维模型中。n维模型就是子结构模型。子结构是仿真中的简化建模方法。在车辆碰撞分析中，将计算成本巨大的整车碰撞模型分离出相关部件，形成可等效替代整车模型的简化结构，利用子结构模型完成后续乘员约束系统匹配优化，可节约仿真时间。伍广等用侧围部件模型替整车模型进行侧面碰撞仿真，发现该方法不仅可以保证分析精度,又可以提高计算效率；［5］白雪飞与王玉琴采用MADYMO 软件中的PSM 方法（prescribed structure motion）建立车体模型，模拟侧面约束系统仿真；［6-7］姜强与程海东均通过PSM 方法完成了侧面约束系统的参数匹配。［8-9］现有研究主要使用MADYMO 软件建立PSM 子结构模型，进行约束系统匹配。对于子结构建模中部件选取以及如何提高仿真精确度的阐述较少。文中利用MOR技术原理，采用LS-DYNA中的接口界面（Interface）法进行侧面碰撞子结构有限元建模，研究子结构模型的关键建模方法，探讨不同加载区域选取对子结构模型精度的影响。

1 模型降阶

系统动力学方程为

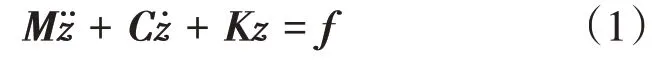
式中：M为质量矩阵；z为物理空间中的位移矢量；C为阻尼矩阵；K为刚度矩阵；f为外力矩阵。模型降阶［10］通过式（1）求解，利用式（2）将简化的解建立线性变换：

式中：T为变换矩阵；za为a集位移矢量。将式（2）代入无阻尼运动方程中，得到超定线性方程：

式（3）中未知数的数量小于方程的数量，式（3）不一定有解。方程两边同乘变换矩阵T的转置，建立降阶系统方程：

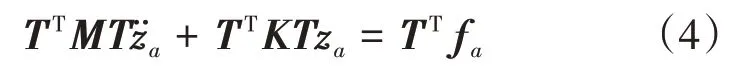
可以求解近似值。得到关于质量和刚度矩阵的简化方程组，表达式为

式中：Mred为降阶质量矩阵；Kred为降阶刚度矩阵。

2 子结构构建与验证

在车辆碰撞仿真过程中，只有部分汽车部件经历非线性塑性变形，远离碰撞冲击的其余部件仅在弹性范围内发生变形，与整车碰撞仿真结果相关度低。在建立可替代整车碰撞仿真模型的等效子结构模型时，将这些部件进行降阶删减，保留其边界上与非线性塑性变形部件存在连接关系的自由度，通过缩减模型进行计算。

2.1 子结构应用流程

用子结构模型代替整车模型进行优化仿真时，需要保证其有足够精度，而模型精度主要取决于边界条件的确定，因此在整个子结构模型建模流程中，子结构区域模型自由度的提取及加载区域的确定尤为重要。子结构方法的基本应用流程见图1。

图1 子结构方应用流程

2.2 离散子结构部件

文中研究在课题组前期完成实验对标的某微型电动车侧面碰撞有限元模型基础上进行［11-12］。在整车侧面碰撞过程中，经历非线性塑性变形的汽车部件主要有车门总成结构以及驾驶员舱相关部件，如地板、座椅、前挡风窗、A柱、B柱等。侧面碰撞子结构模型爆炸视图如图2 所示。在创建侧碰等效子结构模型时，将只经历弹性变形且与整车侧碰相关度低的部件进行删减；同时考虑到位于座椅下方电池组系统的质量和刚度大，对侧碰性能影响大，保留整个电池组部件。保留子结构模型在整车模型中原有的连接方式，如焊点、Rigidbody 以及*Constrained_extra_nodes等。

图2 侧碰子结构模型爆炸视图

2.3 加载区域

子结构模型边界条件一般是指整车模型下该模型边界节点的位移及速度历程曲线［13］，以速度50 km·h⁻¹的可移动变形壁障（movable deformable barrier，MDB）撞击整车的左侧车门［14］进行仿真获得。

子结构模型是在完成整车仿真的基础上进行提取的，用以确定子结构所具有的动态运动特性边界条件。为得到子结构模型的运动特性，对整车模型进行仿真时，将子结构模型（图3）作为加载区域，通过关键字*Interface_component_node 定义子结构模型转换接口数据，计算输出该点集的运动驱动数据［13］。通过命令*Interface_component_file 生成接口转化数据文件，输入点集的位移速度数据。创建子结构模型点集时，模型边界的节点最少选取2排，方便传递扭矩，保证计算稳定。

在整车仿真模型中得到子结构模型边界条件后，进入子结构仿真模型，需完成2 个模型之间节点确认的接口转化，创建关键字*Interface_link‑ing_discrete_node_set，选择子结构模型的点集作为加载对象，同时使用关键字*Interface_linking_file将上述生成的数据文件赋予子结构模型。图3 为提取好的子结构模型节点集。

图3 完整的子结构模型节点集

同复杂的整车侧面碰撞模型相比，子结构模型更加简易，不仅删除了前舱、部分侧围部件以及车身骨架等，还省去了计算成本巨大的MDB。单元数从915 567 减少到121 568，节点数从636 968 减少到119 866；120 ms的侧碰仿真过程，仿真计算时间从10～12 h缩减到1.5～2 h。

2.4 子结构模型与整车模型的一致性验证

为确定子结构模型和整车模型的一致性，从车身变形、车门受力和B柱加速度方面进行对比［15-16］。

2.4.1 车身变形

整车模型（隐藏MDB）和子结构模型在45 ms时刻的变形如图4所示。从图4a中可以看出，车门外板下端a处由于受到MDB 撞击，导致门槛梁处产生转动向外翻转；车门中间b处的内凹区域是由于防撞梁受到MDB撞击后与车门外板发生接触而产生的弯曲变形；门槛梁和防撞梁之间的区域受到MDB 撞击后在c处产生凹陷。对比图4，整车模型与子结构模型在车门a、b、c处的变形区域和变形状况基本一致。表1为整车和子结构模型在3处变形区域的最大位移，可以看出，两者的位移误差较小，满足仿真要求。

图4 45 ms时刻车身变形

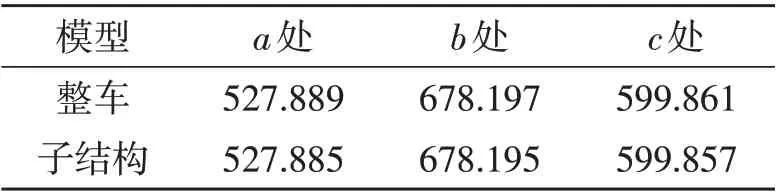
表1 不同变形区域的最大位移mm

2.4.2 车门受力

整车模型和子结构模型的左侧即碰撞一侧车门结构（隐藏车门外板）受力情况见图5，可看出，整车模型与子结构模型的最大应力与吸能集中在防撞梁。整车模型的车门最大应力为785.5 MPa，子结构模型的车门最大应力为812.9 MPa，两者的相对误差为3.49%，属于工程应用的范围。

图5 整车和子结构车门受力

2.4.3 B柱加速度

图6 为整车和子结构仿真模型的B 柱底端加速度对比曲线，碰撞初始，MDB 和整车开始接触，整车和子结构的加速度曲线几乎吻合，主要变形区域为车门外板和车身侧围。整车曲线在27.5 ms 时达到最大加速度-23.12g，而子结构曲线在30 ms时达到最大加速度-22.28g，达到峰值的时间延迟了2.5 ms。子结构B柱底端最大加速度峰值比整车B柱底端最大加速度峰值小0.84g，误差为3.63%，属工程应用范围，这是由于子模型部件的减少使得整体刚度略低于整车刚度。从仿真时间为42 ms 到仿真结束（120 ms），由于整车和MDB 开始逐渐分离，整车和子结构的加速度曲线逐渐降低，该区间内的加速度曲线运动趋势也基本吻合。

图6 整车和子结构B柱底端加速度曲线

为了验证子结构模型在不同速度工况下能否维持良好的一致性，基于40 km·h ⁻¹与60 km·h⁻¹对子结构模型进行研究，整车和子结构仿真模型的B柱底端加速度对比曲线如图7所示，可以看出B柱底端加速度曲线在运动趋势上基本吻合，加速度峰值误差在10%以内，符合工程应用的范围。

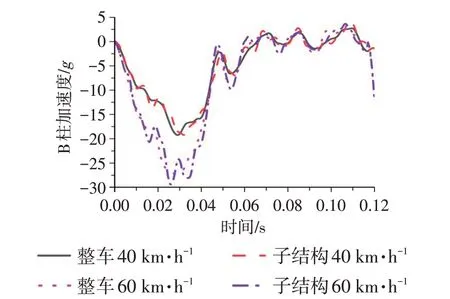
图7 不同速度下整车和子结构的B柱底端加速度曲线

3 子结构模型加载方案对比

为探讨是否可以使用较少数据作为子模型边界条件，对子结构模型边界条件选取不同加载区域方案，从车身变形状况、B柱加速度2个方面与整车模型进行对比分析。在文中子结构模型（原方案）基础上提出3个对比方案：方案1为整个车门区域，方案2为车门的边界区域，方案3为MDB与车门接触的区域，提取区域如图8所示。

图8 子结构区域节点

3.1 车身变形对比

由图9 可知，3 个方案车身变形与整车车身变形基本一致，3处的变形状况与图4无较大差别。

图9 车身变形图

由表2 可知，相比于方案1 和方案3，方案2 的位移误差范围偏大。在方案2的3处变形区域中，b处的最大位移与整车b处的最大位移差达35 mm，相对误差最大，为5.14%。

表2 不同方案的位移mm

图10 为方案2 的b处变形区域的位移时间曲线，可以看出，在0～90 ms，方案2 与整车模型的位移曲线没有明显波动，在90～120 ms，方案2的位移曲线相对整车模型出现一定差异，位移逐渐缩小并偏离整车位移曲线。这是由于在确定边界条件时，方案2 的加载区域没有包含防撞梁与车门外板间的弯曲变形区域，导致该区域缺乏对应的位移速度-时间参数，使得仿真精度下降。

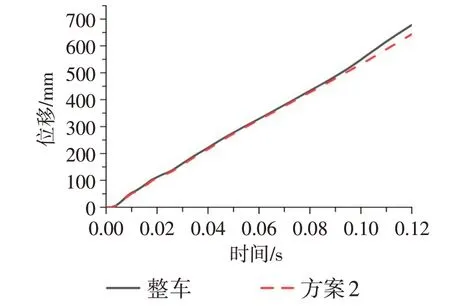
图10 b处形区域的位移时间曲线

综上所述，方案1 和方案3 与整车模型在车身变形和位移时间曲线方面没有明显的差异，具有较好的稳健性。相比于方案1 和方案3，方案2 存在一定的误差。因此在确定子模型加载边界条件时，应将整车发生碰撞的主要区域（MDB的撞击区域）即主要变形区域作为首选条件。

3.2 B柱加速度

图11 为不同加载区域方案的B 柱加速度曲线，可以看出，3 个方案与整车模型的加速度曲线运动趋势基本吻合，曲线波峰也基本对应。3个方案加速度曲线在0～70 ms 与整车模型没有较大偏离，在70～115 ms波峰出现时间比整车模型稍微延迟2～5 ms，总体趋势没有较大的波动。由图11 可看出，在115～120 ms，方案1 与方案3 的加速度曲线随着加速度增大开始偏离整车加速度曲线，方案2的加速度急剧降低，曲线偏离整车加速度曲线。

图11 不同加载区域方案的B柱加速度曲线

子结构模型方案的选取不仅要考虑仿真精度（与整车模型加速度峰值误差），也要适当考虑模型的计算成本。由表3所示，方案2的加速度峰值误差为11.63%，不满足工程应用条件。这是由于方案2 的加载区域是车门边界，没有包含MDB 与整车碰撞的主要接触变形区域，导致碰撞仿真精度降低，这与变形分析的结论是一致的。方案1与方案3 在选取加载区域时都包含了碰撞的主要接触变形区域，两者的加速度峰值误差皆属于工程应用范围，但方案1加速度误差大于方案3；由于方案1的子模型边界条件加载区域占比高于方案3，方案1的计算时间比方案3增加近32%，综合加速度峰值误差和计算成本2 个因素，方案3 优于方案1。方案1 的加速度误差并没有因为其选择占比区域的增加而减少，误差较方案3增加5%，说明牺牲计算成本不能提高计算精度，加载区的合理选取可以找到计算成本较低、精度较高的区域，选择区域为门槛梁上端MDB 撞击区，即碰撞的主要接触变形区域，可以较好体现整车的碰撞特性。

表3 不同方案对比数据

方案3的仿真精度与计算成本都较好，与原方案进行对比。原方案的仿真精度高于方案3，与方案3 的加速度峰值误差相差1.17%；对比图6 和图11，原方案与整车模型的加速度曲线吻合度高，比方案3更加稳定，这是由于原方案的加载区域考虑了电池组，实际碰撞中电池组在碰撞后期介入变形，使得原方案与整车模型的受力传递高度近似；同时由表3 可知，在计算成本上，原方案区域占比提高，其计算时间约为方案3的3倍。

通过对比车身变形、位移时间曲线以及B柱加速度曲线，表明在确定边界条件时，首选碰撞的主要接触区域，驱动碰撞主要变形区域的运动参数。综合考虑计算成本与精度，在侧碰子模型建立中，可以选取碰撞侧门槛梁上与MDB接触的主要变形区域为子模型的加载区域。不考虑计算成本的条件下，对于电动汽车，子模型加载区域考虑电池组，加速度曲线运动趋势更加稳定。考虑原方案子结构模型计算成本在可接受范围内，后续约束系统匹配可在该模型基础上进行。

4 结论

侧面碰撞仿真计算时间长，不利于后续约束系统匹配工作，为此进行子结构模型精度的研究，得到以下结论：1）综合考虑精度及计算成本，在确定侧碰子模型边界条件的加载区域时，可以只提取主要变形区域，即车辆与MDB 接触区的点集运动数据；2）为保证子结构模型加速度曲线在整体碰撞过程中与整车的一致性，在电动汽车侧碰子结构模型中，除主要变形区域外，建议选取整个电池组作为子模型边界条件加载区域；3）将原方案作为最优方案，其B 柱加速度最大峰值误差仅为3.63%，且加速度曲线的运动趋势与整车模型的曲线运动趋势吻合，为后续约束系统匹配奠定了基础。