基于小波与嵌入式零树编码的锈蚀图像压缩方法

陈法法 李 振 成孟腾 陈保家 肖文荣

(三峡大学 水电机械设备设计与维护湖北省重点实验室,湖北 宜昌 443002)

在水工机械装备的定期维护检修中,通常会采集大量钢结构表面的锈蚀图像.随着采集硬件的持续升级,所采集锈蚀图像的分辨率越来越高[1-2].较高的图像分辨率有利于锈蚀图像的识别与检测;但是,过高的分辨率并不利于锈蚀图像的无线传输和处理[3-4].

通过图像压缩技术可以降低原始图像的冗余信息,增强图像数据之间的独立性,提升图像的传输和处理效率[5-6].传统采用二维离散小波变换的图像压缩方法将图像分解为不同方向、不同尺度的子图像,通过子图像的量化编码实现图像的数据压缩[7-8].如:宋蓓蓓等对小波高、低频子带数据进行码率预测,并对多个编码通道进行率失真优化,实现了自适应码率控制的图像压缩[9].王浩等对稀疏矩阵进行向量稀疏度的均匀化处理,并采用奇偶校验矩阵对其进行观测,通过译码算法实现图像压缩[10].杨楚皙等将空域图像转换到小波变换域,在小波域完成特征匹配,实现了图像的压缩[11].

上述方法对普通图像具备一定的压缩效果,但锈蚀图像与普通图像存在一定差异,锈蚀图像的细节信息更为丰富,锈蚀表面多呈现不规则的粗糙面,且不同材料发生锈蚀时会呈现不同的颜色特征,在对其进行图像压缩时,一方面需要避免彩色锈蚀图像的细节特征在压缩过程中丢失,另一方面也需要充分结合人眼视觉特性,避免锈蚀图像在压缩重构后其表观质量变差[12].传统二维离散小波在对图像进行压缩时通过将阈值引入小波系数量化的过程,将高于阈值部分保留,低于阈值部分赋予常数,虽然在压缩比方面有一定的提高,但并未结合特定目标图像分析各通道信息,从而导致部分细微的锈蚀特征在图像压缩后无法恢复.因此,基于二维离散小波的传统图像压缩方法存在局限性[13].

嵌入式零树编码(embedded zerotree wavelet coding,EZW)通过利用不同分辨率、不同方向子带之间小波系数的相似性构造零树结构,通过多次扫描,依照重要程度对小波系数依次编码,以此更好地保留锈蚀图像的细节特征,同时也提升压缩后图像的表观质量[14].

针对彩色锈蚀图像的细节特征在压缩过程中丢失的问题,本文将原始图像的颜色空间转换为YCb-Cr颜色空间,其中分量Y 与其它两个分量相互独立,YCbCr颜色空间在图像压缩中允许更大的压缩比而不会对感知图像质量产生显著影响.为了使压缩重构后的图像在主观评价上得到更有效的保障,本文在传统EZW 基础上引入对比敏感度函数,根据人眼视觉特性对不同方向子带系数进行加权处理.

为此,本文基于小波变换和嵌入式零树编码,通过嵌入对比敏感度函数,设计基于小波与嵌入式零树编码的锈蚀图像压缩方法,在细节特征尽可能少的损失下,实现锈蚀图像的高质量压缩处理.通过溪洛渡水电站安装前的压力钢管锈蚀图像的实测数据集验证本文方法的有效性和优良性.

1 基础理论

1.1 小波变换

设一维连续信号f(t)是平方可积函数,记为f(t)∈L2(R),ψ(t)为基本小波,则信号f(t)的一维连续小波变换为:

式中:WTf(a,b)为f(t)的连续小波变换;a为尺度伸缩因子,a∈R,a≠0;b为平移因子,b∈R;ψa,b(t)为积分核.

二维小波变换是将二维信号先进行一维行变换,之后再进行一次列变换,则信号f(x,y)的二维连续小波变换为:

式中:WTf(a,bx,by)为f(x,y)的二维连续小波变换;bx、by分别为x、y两个维度上的平移因子,bx、by∈R.

将尺度因子a和平移因子b进行离散化,相应的二维离散小波变换为:

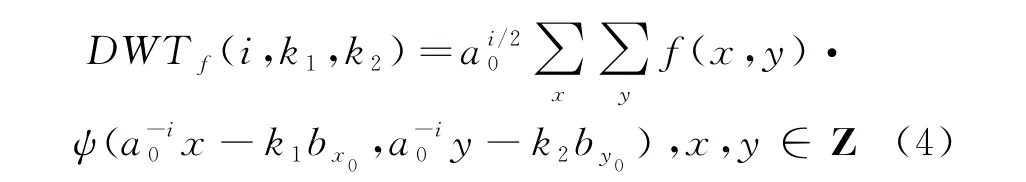
式中:bx0、by0为常数,i、k1、k2均为整数.

在对图像数字信号处理的过程中,图像经小波分解后得到低频子带LL 和高频子带LH、HL 和HH.小波分解示意图如图1所示.↓表示下采样,G 为高通滤波器、H 为低通滤波器.

图1 小波分解示意图

1.2 嵌入式零树编码

嵌入式零树编码应用于图像压缩时,首先将原始图像通过小波变换转换到变换域中,然后对小波系数进行扫描、量化、分类以及排序,最后经过熵编码和后处理将数据流转换为占用空间小且传输速度快的比特流进行输出.其基本流程如下:

Step1:设定阈值t0,t1,…,tm,筛选重要小波系数.

Step2:进行“Z”字型主扫描.

以给定的阈值对小波系数a进行分类:①重要系数POS:当前系数a为正数且其a≥t;②重要系数NEG:当前系数a为负数且其|a|≥t;③零树根ZTR:当前系数|a|＜t,且在该系数的所有子系数中不存在重要系数;④孤立零点IZ:当前系数|a|＜t,且在该系数的所有子系数中,存在子系数|a|＞t.将|a|≥t的重要系数保留,对|a|＜t系数省略,进而大幅度削减所需编码信息.

Step3:辅扫描.

通过构造量化器,对Step2中的重要系数进行量化编码,从而提高解码端重要系数的重构精度.量化区间为[tm,2tm],当重要系数处于[tm,1.5tm)时,将其量化为0,在解码阶段时重构值设置为1.25tm;当重要系数处于[1.5tm,2tm]时,将其量化为1,在解码阶段时重构值设置为1.75tm.

Step4:重新排序.

为便于设置第i+1次扫描所用的量化区间,提高解码精度,依据辅扫描中划分的区间对重要系数进行排序,按照幅值从大到小的原则重排重要系数.

Step5:输出编码符号流.

单次扫描后,输出信息主要包含两类:一类是扫描表及阈值序列,传输给解码端;另一类为下轮扫描信息.若继续扫描则重复Step1-Step4且将阈值减半,同时不对已扫描出的重要系数再次扫描,逐次逼近量化,直到编码结果满足精度要求或达到编码限制为止.

嵌入式零树编码算法的整体流程如图2所示.

图2 嵌入式编码流程图

2 本文方法流程

基于小波原理设计了一种融合对比敏感度函数和嵌入式零树编码的图像压缩模型,如图3所示.

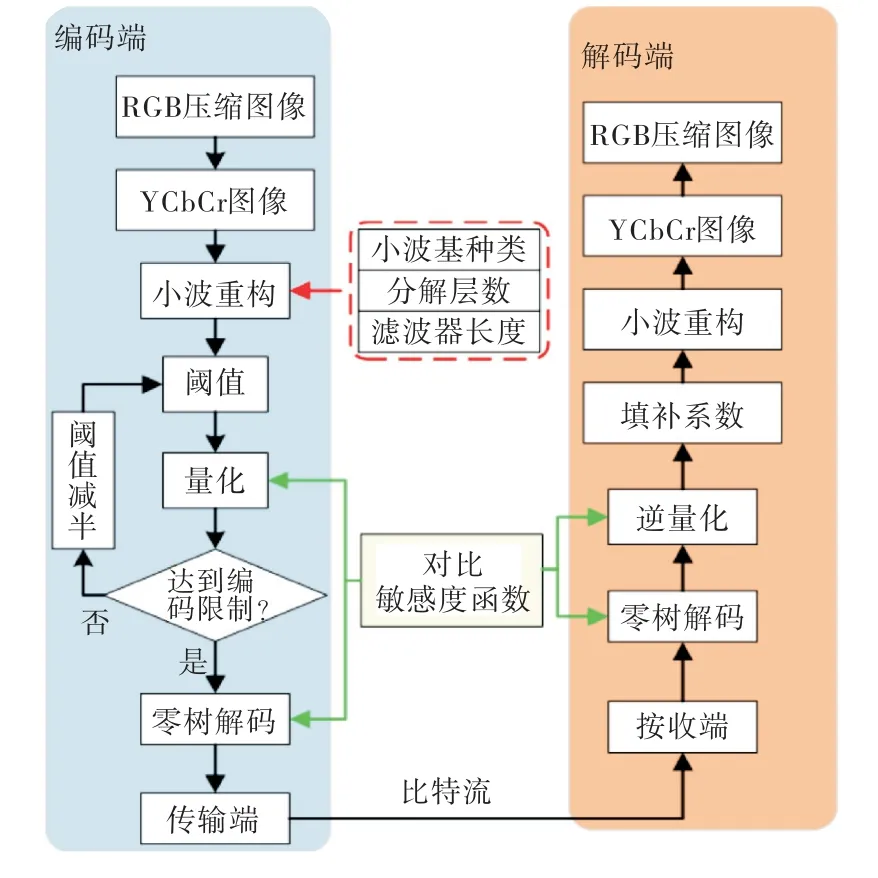
图3 图像压缩重构流程图

在编码端,首先将彩色锈蚀图像从RGB 空间转换到YCbCr颜色空间,采用Haar小波基函数分别对Y、Cb、Cr三通道分量进行处理;然后结合对比敏感度函数中各方向子带的权重对水平、垂直以及对角高频子带中小波系数进行加权处理;最后采用零树编码对加权后的各子带进行量化、编码,由此得到压缩后的图像.

在解码端,首先分别对Y、Cb、Cr三个通道分量进行零树解码与反量化;然后结合编码端水平、垂直以及对角高频子带的各自权重还原权值;接着分别对三通道小波系数采用小波逆变换得到Y、Cb、Cr颜色空间的重构分量;最后将Y、Cb、Cr三通道分量合并后还原到RGB 颜色空间,由此得到压缩重构后的锈蚀图像.

图像经过小波分解后得到低频子带、水平高频子带、垂直高频子带以及对角高频子带4 个方向的分量.对人眼的视觉特性而言,水平、垂直以及对角各高频子带的影响并不相同.因此,在传统EZW 基础上引入对比敏感度函数A(f)对不同方向子带系数进行加权处理.

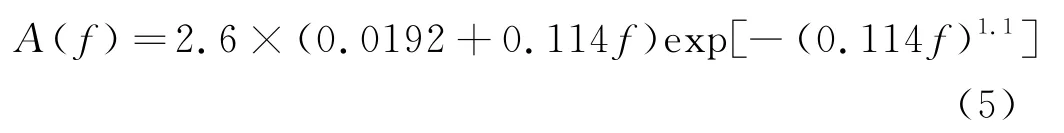
根据对比敏感度函数特性曲线(图4)得知,人眼对空间频率[0.03,0.25]之间的信息最为敏感.为此,对三层小波分解后水平分量、垂直分量以及对角分量的小波系数进行加权,从人眼视觉上改善压缩图像质量,其中低频分量、水平方向高频分量、垂直方向高频分量、对角线方向高频分量的权重系数分别设为1,2.56,2.35,1.79[15].

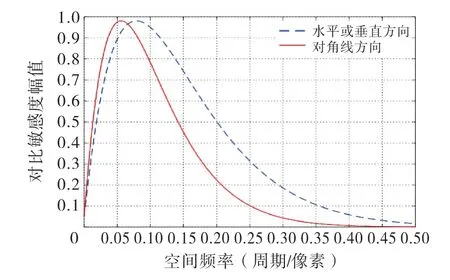
图4 对比敏感度函数特性曲线

3 实 例

3.1 实验数据

为了验证本文方法的有效性和适用性,采用溪洛渡水电站安装前的压力钢管锈蚀图像作为测试图像,在所拍摄的图片中随机选取20张尺寸规整后的锈蚀图像进行测试和验证,规整尺寸为256×256×8bit.

3.2 评价指标

1)图像压缩比CR:用于衡量锈蚀图像压缩前后存储空间大小的变化.其值越大,所占存储空间越小,压缩效果越好.

式中:m、n分别为图像的长和宽;P(i,j)、PR(i,j)分别为图像压缩前后图像像素点对应的比特数.

2)峰值信噪比PSNR:用于衡量压缩后图像的失真程度.其值越大,图像重构质量越高,失真度越低.

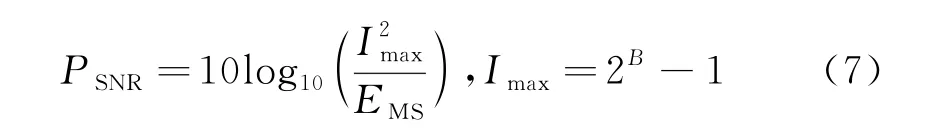
式中:EMS为压缩前后图像像素的均方误差;Imax为图像的最大像素值;B为图像的位深,经过反复实验,本文采用uint8型图像.

3)结构相似度SSIM:用于衡量压缩前后图像的结构相似性.其值越大,图像相似度越高.

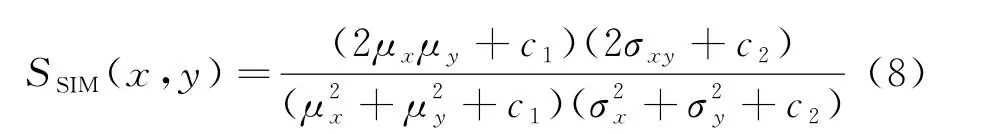
式中:μx和μy分别为压缩前图像x与压缩后图像y的像素均值;σx和σy分别为其像素方差;σxy为两图像的协方差;c1、c2均为整数.

3.3 实验结果对比分析

1)与传统算法的对比分析

为了验证本文图像压缩模型的有效性和优越性,选择与传统图像压缩算法:主成分分析、小波变换、嵌入式零树编码(EZW)作为对比测试.采用相同的20张测试图像,不同算法的图像压缩结果如图5所示.

图5 不同算法的锈蚀图像压缩效果对比

从图5可以看出,不同方法都可以对锈蚀图像进行压缩处理,但是仅从人眼视觉对输出的压缩图像进行观察,很难辨别出不同算法的压缩效果.为了定量比较不同算法对锈蚀图像的压缩效果,使用直方图进行验证与分析,不同算法对锈蚀图像压缩后的直方图如图6所示.

图6 不同算法处理后的直方图对比

从图6可知,原始图像的灰度值集中分布在75至175之间,小波变换方法的灰度值集中分布在75至175之间,与原始锈蚀图像相比,在B 分量上有信息丢失;主成成分分析的灰度值集中分布在65 至165之间,与原始锈蚀图像相比,R 分量和B 分量均有不同程度的信息丢失;EZW 方法的灰度值集中分布在75至175之间,与原始锈蚀图像比较,在B分量上有少量信息丢失.本文方法得到的图像直方图中,灰度值分布与原始图像高度一致,图像颜色和纹理特征得到更好的保留.

为了定量评价不同算法的图像压缩效果,采用定量评价指标做对比分析,各算法在20张锈蚀图像上评价指标的平均值见表1.

表1 不同算法在锈蚀图像上的评价指标均值

从表1可以看出,主成分分析与小波变换都可以在一定程度上进行锈蚀图像压缩,但是这两种算法均无法同时兼顾图像压缩比和峰值信噪比指标.在主成分分析中的图像压缩比最高达到1.071,但是对应的峰值信噪比为33.851dB;在小波变换中的图像压缩比最高达到1.165,但是对应的峰值信噪比为30.251 dB.传统EZW 算法的图像压缩比指标可达到1.673,但是其重构图像的平均峰值信噪比为39.566.本文算法通过嵌入对比敏感度函数,其峰值信噪比指标达到了42.064dB,平均压缩指标达到1.281,结构相似度接近99.5%,在保证重构图像质量的同时压缩效果最好.

2)YCbCr空间各分量图压缩结果对比

为了更好地说明本文图像压缩模型的编码质量和压缩图像质量,在测试集中任选1张锈蚀图像,分别对该图像YCbCr颜色空间中各分量图进行压缩编码,采用haar小波基函数,扫描次数设置为8,不同分量图的图像压缩结果如图7所示.

从图7可以看出,通过本文方法压缩重构后,无论是各个分量图还是其合成图,从视觉上看不出压缩前后的差异.通过更深层次的对比各图压缩前后的存储空间,可以发现,Y 分量图压缩前后的存储空间分别为38.9KB和36.2KB,压缩幅度较小;Cb分量图和Cr分量图压缩前后的存储空间变化幅度较大.这是由于Y 分量图包含了原始图像的亮度、结构等诸多信息,大幅压缩该分量将导致图像失真和畸变,而Cb分量图和Cr分量图主要包含图像的色度等细节信息,大幅压缩该分量对图像整体质量影响较小.

图7 YCbCr空间不同分量图的图像压缩结果

3)应用案例分析

为了验证本文算法与传统EZW 算法在工程应用方面的泛化推广能力,采用实际工程中测试的20张锈蚀图像进行测试分析.将20张锈蚀图像分别输入到本文图像压缩模型和传统EZW 图像压缩模型,经压缩处理后,其输出结果如图8所示.

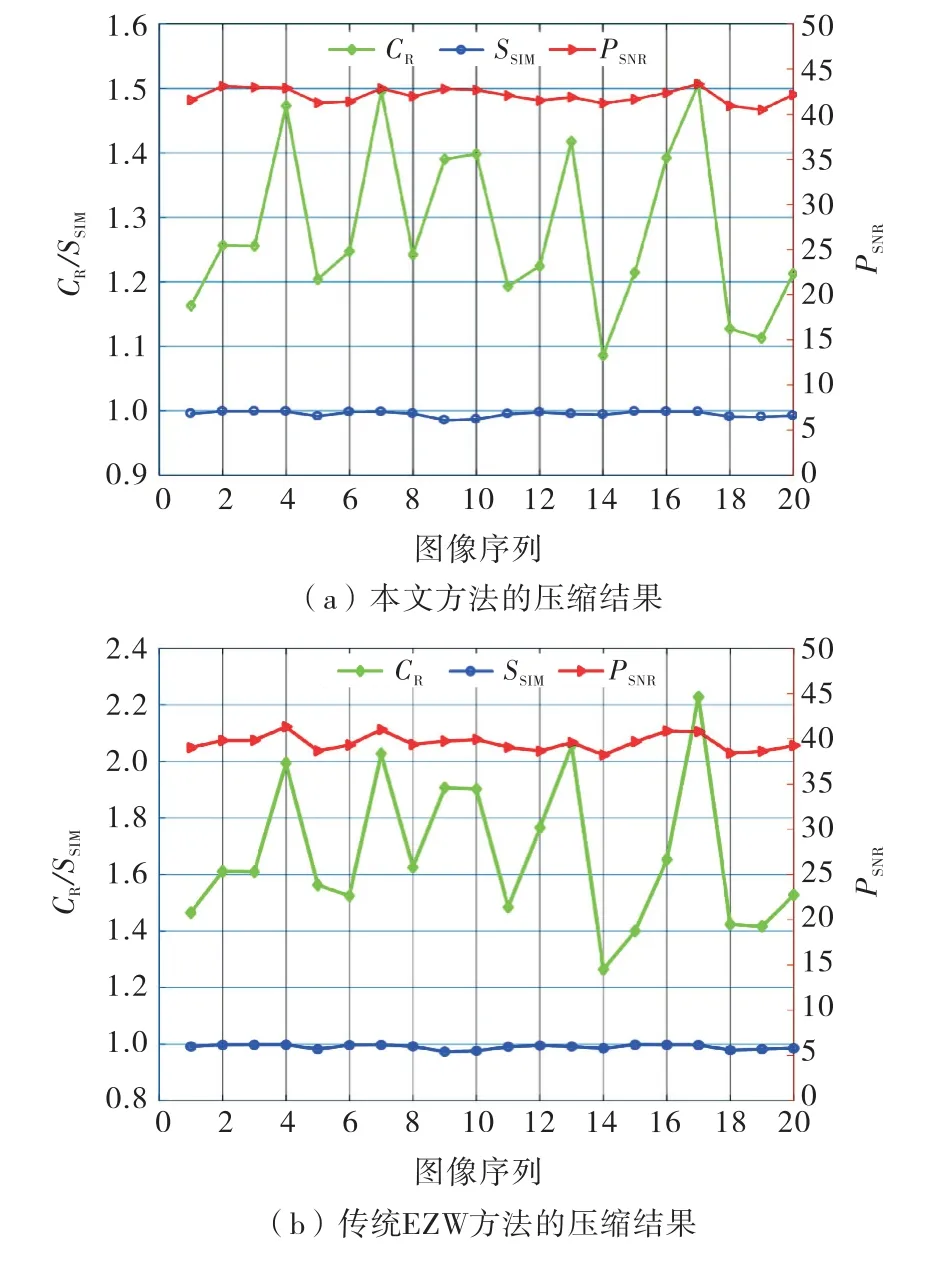
图8 本文算法与传统EZW 算法的压缩结果

从图8可以看出,本文基于小波与嵌入式零树编码的图像压缩方法,20张实际工程中获取的锈蚀图像的峰值信噪比指标均超过人眼的视觉分辨能力40 dB,通过目测已经无法分清图像压缩前后的差异.而使用传统EZW 算法获取的锈蚀图像的峰值信噪比指标仅有部分超过40dB.因此本文方法对压缩后锈蚀图像的峰值信噪比指标有一定的提升.

较之传统EZW 算法,本文方法在图像压缩程度及压缩后重构图像的质量方面均表现出优势,能够有效提升图像的传输速度和后续的图像处理效率.

4 结论

为了提高高分辨率锈蚀图像的传输效率和处理速度,设计了一种基于小波和嵌入式零树编码的锈蚀图像压缩方法.得出以下结论:

1)采用小波变换对待分割锈蚀图像进行分解,采用嵌入式零树编码对小波系数进行量化编码,在保证压缩后图像质量的同时,有效降低了图像的存储空间.

2)使用YCbCr颜色模型分离待分割锈蚀图像三通道分量,可以增加码流传输比,减少数据传输量.引入对比敏感度函数对不同子带进行加权,从人眼视觉上提升了压缩后图像的感观质量.

3)通过对溪洛渡水电站安装前的压力钢管锈蚀图像进行分析,对于待分割锈蚀图像的平均压缩比达到1.281,压缩后的图像峰值信噪比超过40dB,具备一定的有效性和实用性.