基于基波电压检测的并联型有源电力滤波器设计

代 灿，李 沁，陈坤燚，曾 伟，赵国军

(湖北民族大学 智能科学与工程学院，湖北 恩施 445000)

随着科学技术的发展与进步，电力电子器件得到了广泛应用，为人们的生活带来了极大便利，但同时对电网的稳定运行也造成了一定影响，谐波的产生就是这些影响中突出的问题.目前，对谐波高效、快速地抑制成为了人们追求的目标.相对于无源电力滤波器，有源电力滤波器(active power filter,APF)因具有更好的动态响应性能、体积小等优点而被广泛应用[1].有源电力滤波器的传统控制方法是通过谐波检测环节检测出谐波指令电流，再由控制器进行闭环电流跟踪控制，产生与指令电流大小相等、相位相反的补偿电流来补偿负载产生的谐波电流，因此谐波检测环节就成了整个控制过程的关键[2].

为精确、快速地检测出负载电流的谐波分量，学者们开展了大量研究.吕自波等[3]采用逐次分序的谐波检测算法，将滑窗离散傅里叶变换(discrete fourier transform,DFT)和对称分量法相结合，提高了检测精度，但计算量较大.翟晓军等[4]提出一种基于傅里叶变换的改进算法，其原理简单、计算速度快，但系统基频的偏差可能会导致该方法出现误差.潘国兵等[5]针对滤波器的带宽和响应时间上的矛盾，提出一种Z-域下快速谐波电流检测方法，提高了响应速度，但仍有一定延时存在.

传统控制方法中谐波检测环节必不可少，而谐波检测环节中含有低通滤波器，只要谐波检测环节存在就很难避免检测的延迟与误差，因此，无谐波检测的滤波方法就有了研究价值.田军等[6]和陈煜达等[7]提出了基于磁通补偿原理的APF，避免了谐波检测环节，但基于磁通补偿的APF系统的内阻抗对滤波特性有很大影响，而且谐波磁通补偿的条件很难严格满足.同样，魏学良等[8]采用电源电流控制策略，避免了谐波检测环节，但未考虑APF的容量问题.

综上所述，基于等效虚拟阻抗的设计方法，提出一种基于基波电压检测的并联型有源电力滤波器.通过检测公共连接点(point of common coupling,PCC)的基波电压，以该基波电压为参考信号，使逆变器的输出电压等于PCC的基波电压，逆变器对基波呈现高阻抗，同时通过对逆变器控制器的设计使其对谐波的虚拟阻抗近似为零，迫使谐波电流流入逆变器支路，达到滤波的目的.

1 系统结构及工作原理

并联型有源电力滤波器的电路原理如图1所示.逆变器的输出滤波器采用LC滤波器，用于抑制逆变器产生的开关纹波.US为网侧电压，ZS为网侧的阻抗，Rd、Ld分别为负载侧的电阻和电抗，Ud为逆变器直流侧电压，Ih为模拟谐波电流源.

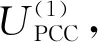
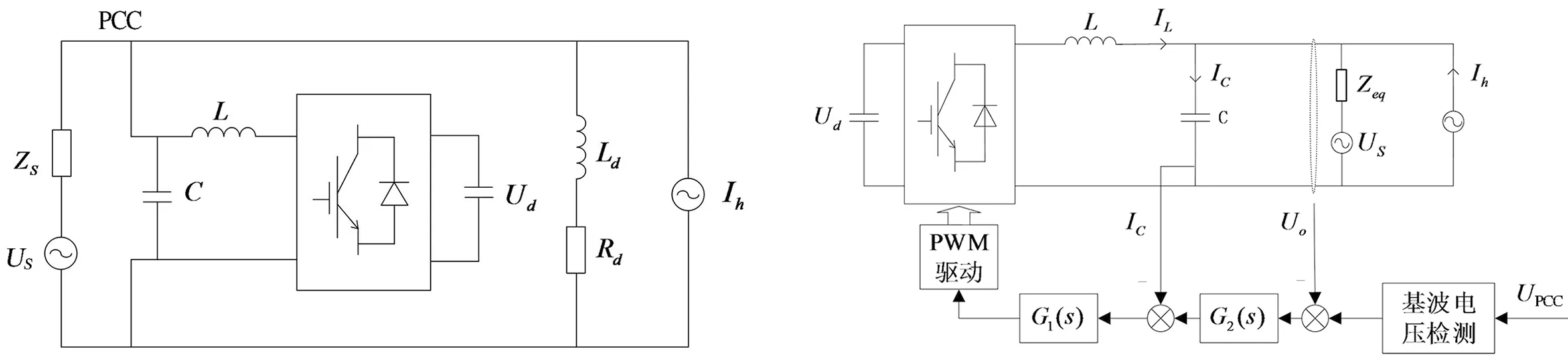
图1 并联型有源电力滤波器电路原理 图2 并联型有源电力滤波器控制原理

1.1 逆变器基波等效阻抗分析

控制APF使其输出幅值为Uo的基波电压，将APF等效成电压为Uo的电压源，等效电路如图3所示.图3中，IS为网侧电流，Id为负载侧电流，Io为逆变器支路电流.

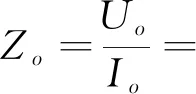
(1)

即APF的基波等效阻抗为无穷大，APF支路无电流流入，网侧的基波电流全部流入负载，因此APF不会影响负载的正常工作和电网的能量传输.

1.2 谐波抑制作用分析

APF输出为基波电压时，可将负载谐波源看作一个大小为Ih的电流源，其等效电路如图4所示.图4中，Zh为逆变器的虚拟谐波阻抗.由图4可推出，系统侧的谐波电流为

(2)

由式(2)可知，通过控制器设计使Zh→0时，Ish→0，即可将APF看作对谐波呈现为阻抗近似为零的虚拟阻抗，绝大部分谐波电流将流入APF支路，从而达到滤波的目的.

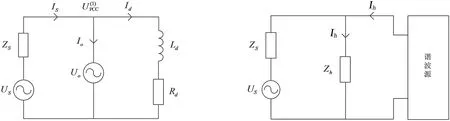
图3 基波等效电路图4 谐波等效电路Fig.3 Fundamental equivalent circuit Fig.4 Harmonic equivalent circuit

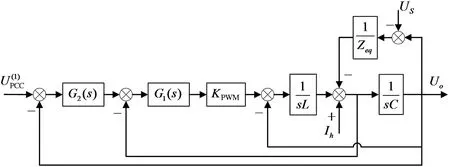
图5 有源电力滤波器的控制框Fig.5 Control block diagram of active power filter

2 谐波虚拟阻抗调节方法

APF的等效谐波虚拟阻抗Zh直接决定有源电力滤波器的滤波效果，由式(2)可知，Zh应尽量小，理想情况下Zh=0.考虑所设计的有源电力滤波器只输出基波电压，无法真正实现Zh=0，因此采用了Zh→0的方法来实现.若Zh→0，即APF对谐波呈现近似为零的虚拟阻抗，则实现有效滤波.

根据图2所示原理图可推出有源电力滤波器的控制框，如图5所示.图5中L和C构成LC滤波器，忽略滤波电感和滤波电容的寄生参数.采用双闭环控制策略，G1(s)为内环控制器的传递函数，G2(s)为外环控制器的传递函数，KPWM为逆变器等效增益，Zeq为有源电力滤波器的输出端口等效阻抗.

因比例控制器具有抑制LC滤波器谐振尖峰的特点[10-11]，因此内环电流控制器采用比例控制器，用Kp1表示，外环用Kp2表示.

由图5可知，谐波阻抗的传递函数为

(3)

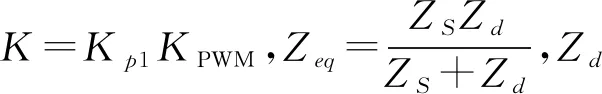
式(3)中，分母的三次项系数LC的值远远小于二次项系数，因此忽略分母中三次项的影响，则可得到Zh→0的满足条件为：分母的二次项系数远大于分子的二次项系数，即

(4)

式(4)中，C、L、Zeq均为已知量，可以得出减小谐波阻抗Zh的方法为：增大K的值，即在设计内环控制器时增大Kp1的值.且由式(4)可推出Kp1的最小取值为200.参数设定满足该条件则逆变器的谐波虚拟阻抗近似为零，在此基础上无需进行谐波检测，只需测量基波电压作为调制波，产生脉冲宽度调制(pulse width modulation,PWM)信号，控制逆变器输出等于公共点基波电压，即可实现滤波.由于Kp1的值与L和C的取值相关，为留取一定的裕度，取Kp1=300.

表1 系统参数Tab.1 System parameters

3 理论验证与仿真分析

为验证提出的无谐波检测APF的正确性和有效性，基于图1和图2的并联型有源电力滤波器拓扑结构图和原理图，在PSCAD/EMTDC中搭建如图6所示的仿真模型.负载采用电流源和阻抗并联的方式模拟谐波源，由于电力系统负载的主要谐波含量为3、5、7次[12]，因此模型中模拟谐波电流源设置为含3、5、7次谐波.模型中的系统参数设定如表1所示.

控制电路采用双闭环控制策略，其中，内环电流控制器采用比例控制器，根据上文推导，取比例系数Kp1=300；外环电压控制器采用比例积分(proportional integral,PI)控制器，可根据典型系统整定法整定其参数[13-14]，取其比例系数Kp2=9.50，积分系数Ki=909.09.

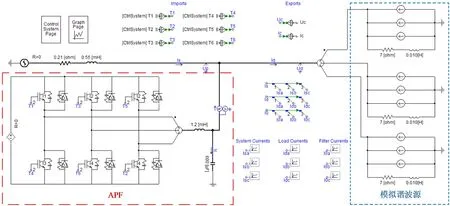
图6 仿真模型Fig.6 Simulation model

3.1 滤波有效性分析

投入APF前后网侧电流Is的波形如图7所示.由图7可知，投入APF前，电流畸变较大；投入APF后，网侧电流波形接近于正弦波，滤波效果理想.此外，相比于传统型APF，无谐波检测型APF网侧电流更接近于标准正弦波，滤波效果更加理想.

采用有源电力滤波前后网侧电流的总谐波畸变率(total harmonic distortion,THD)如图8和图9所示.由图8可知，采用APF前的谐波含量较高，THD为50.75%.

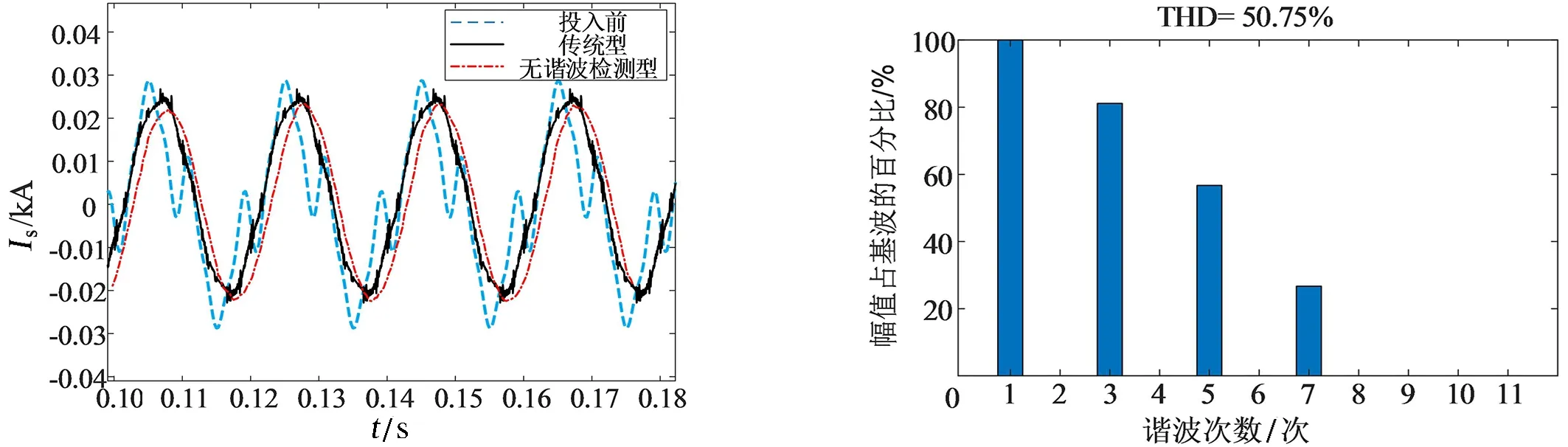
图7 投入APF前后网侧电流波形 >图8 滤波前网侧电流THD Fig.8 Grid side current THD before filtering

由图9可知，经APF滤波后，网侧电流THD显著下降，谐波均能得到有效抑制，但相比于传统并联型APF滤波，采用所设计APF的THD值由2.36%降为0.52%.其原因在于传统型APF是基于谐波检测进行谐波电流注入实现滤波，由于分辨率的影响谐波分析过程存在频率泄露，造成测量误差.而所设计的APF无需谐波检测，通过满足任意谐波下其谐波虚拟阻抗都近似为零实现滤波，从而消除测量误差，滤波效果更好.

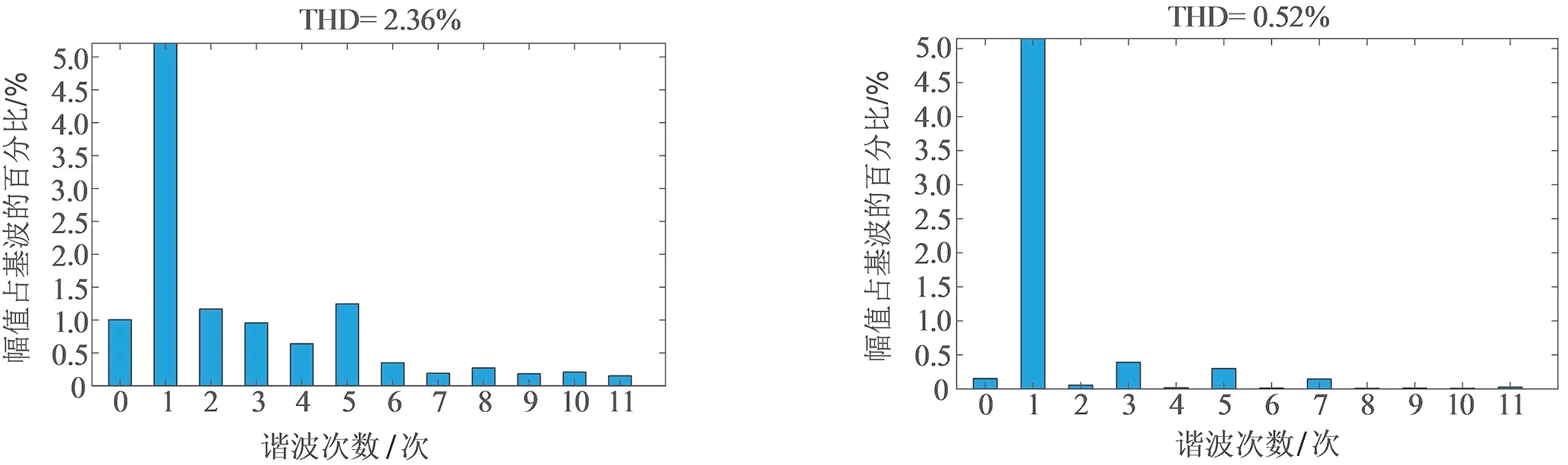
(a) 传统并联型APF (b) 无谐波检测型APF图9 滤波后网侧电流THDFig.9 Filtered grid side current THD

3.2 电网频率波动的影响分析

传统的谐波电流注入法不考虑电网参数的变化，且测量误差与谐波源有关，因此当电网频率发生波动时，传统并联型滤波效果较差.考虑电网系统中电压频率波动的范围[15]，本文验证了电网频率为(50±0.5) Hz时的滤波效果.

电网频率波动时，传统型APF和无谐波检测型APF投入前后网侧电流波形如图10所示.由图10可知，当电网频率波动时，无谐波检测型APF滤波后的网侧电流波形更接近于标准正弦波，滤波效果明显好于传统型APF.传统型APF网侧电流THD为10.92%，已无法满足THD≤5%的国家标准[16]，其原因是当电网频率波动时，传统型APF谐波检测仍是基于基波为50 Hz进行快速傅里叶变换(fast fourier transform,FFT)分析，因此会产生较大误差，导致滤波效果下降.而无谐波检测型APF因其不含谐波检测，受电网频率波动影响小，其网侧电流THD为2.68%.虽然滤波效果有所下降，但仍能满足国家标准，验证了本设计在电网频率波动时的有效性.

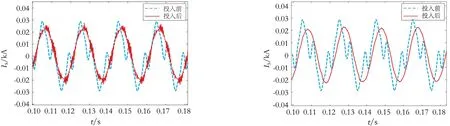
(a) 传统并联型APF (b)无谐波检测型APF 图10 频率波动时投入APF前后网侧电流波形Fig.10 Current waveform of the grid side before and after the APF is applied when frequency fluctuates

3.3 滤波器容量分析

基于谐波检测方法的传统并联型APF输出的电压为基波电压，输出的电流为与谐波大小相同、极性相反的补偿电流，而所设计的无谐波检测APF输出的电压也是基波电压，但是由于满足谐波虚拟阻抗近似为零的条件，因此输出的电流为幅值很小的基波电流.基于谐波检测的传统型APF和所设计的无谐波检测型APF逆变器侧的功率输出如表2所示.

表2 逆变器输出功率比较Tab.2 Comparison of inverter putput power

由表2可知，传统谐波检测型APF控制逆变器产生谐波补偿电流，而无谐波检测型APF疏导负载侧的谐波电流流入逆变器支路，并不产生谐波电流.因此，相对于传统谐波检测型APF，无谐波检测型APF的输出视在功率更小，即容量更小，有利于降低滤波器的生产设计成本.

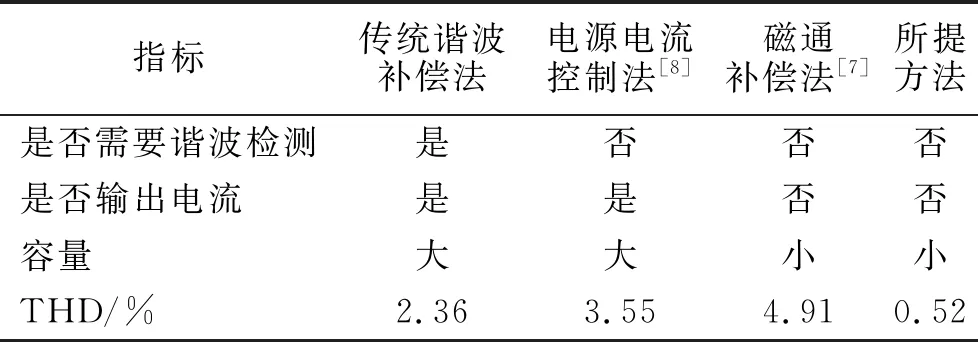
表3 滤波方法比较Tab.3 Comparison of filtering methods

3.4 滤波方案对比

结合上述分析，将所提方案与其他滤波方案进行对比，如表3所示.传统谐波补偿法存在谐波检测环节，有检测误差影响滤波效果的问题；电源电流控制法虽无需进行谐波检测，但同样是输出谐波补偿电流，因此需要考虑APF的容量问题；磁通补偿法与所提基波电压检测法都无需谐波检测环节，且都无需考虑容量问题，但基波电压检测法在滤波效果上存在明显优势.

4 结论

所提出的无谐波检测的并联型有源电力滤波器，通过合理选择控制器参数，当逆变器产生的基波电压与公共连接点的基波电压相等时，该有源电力滤波器可以实现不对网侧基波电流分流，而对各次谐波电流呈现近似为零的低阻抗，从而达到理想滤波效果.通过仿真实验验证了该有源电力滤波器的有效性.此外，由于设计的有源电力滤波器只需检测与跟踪基波电压，相比谐波电流注入法的传统型有源电力滤波器，其无需谐波检测，检测误差小；电网频率波动(±0.5 Hz)情况下适应性强；输出电流小，无需考虑容量问题，有效降低了滤波器的生产设计成本.