一维资产价格模型BCB曲线和周期结构

顾恩国，倪俊，何昭辉

（中南民族大学 数学与统计学学院，武汉 430074）

自文献［1］运用牛市熊市市场模型解释金融市场中的复杂动力学，已有许多论文研究市场参与者的交易行为与不可预测的价格动态之间的关系［2-6］，旨在寻求金融市场内部的影响因素.在他们的模型中，图表分析师、基本面分析师和造市商，这3种市场参与者对价格趋势的变化起着重要作用，本文分析的模型属于此类.

作为非光滑映射所特有的边界碰撞分叉（BCB），与传统光滑映射分叉不同，其分叉与特征值无关并且导致吸引子结构的急剧转换.例如从不动点到混沌的突然切换，这是光滑映射分叉不可能出现的现象.BCB属于接触分叉的一种，例如，周期吸引子的某一周期点与非光滑点（也称为关键点）发生接触，将会发生BCB，这会导致周期轨的出现和消失.文献［7-9］介绍了复杂度和周期叠加（period adding）结构.在一维情况下，有一个非光滑点映射的两个线性函数的斜率为正且小于1，则在两个不动点均为虚拟的参数范围内填充以周期叠加分叉结构组织的周期性区域.即只有周期吸引子存在，且分叉结构中所有吸引周期环的周期和旋转数遵循Farey求和规则.此外，当n≥1时，从所谓的基本周期的符号序列（RLn，LRn）开始，通过序列的并置得到了分叉结构中周期的符号序列.文献［6］和文献［10］将首次返回映射分别用于周期叠加和周期共存的分析.文献［11-12］研究了左边为线性、右边为幂函数的映射族的边界碰撞，以上研究主要集中在只有一个非光滑点的映射.应该指出基于经济学背景的有两个非光滑点的BCB结构也有相关研究［2-4］，但是多个不连续点映射的BCB结构理论远远没有完善.本文将研究文献［13］得到的具有两个不连续点的分段线性映射，讨论其为压缩映射情况下的周期区域结构.

1 动力学模型

文献［13］基于文献［4］模型的简化，即对图表分析师和基本面分析师的行为进行简化假设，进而得到如下有3个线性子系统的模型：

该模型的主要特征是3个线性子系统的斜率均相同.文献［13］主要研究的是递增扩张映射(s＞0)模型的混沌吸引子的边界碰撞分叉.本文继续研究该映射，在假设条件：

下研究参数平面(s，m)上的周期区域结构.图1是参数平面(s，m)的二维分叉图，本文将揭示此图的3块周期区域结构规律.

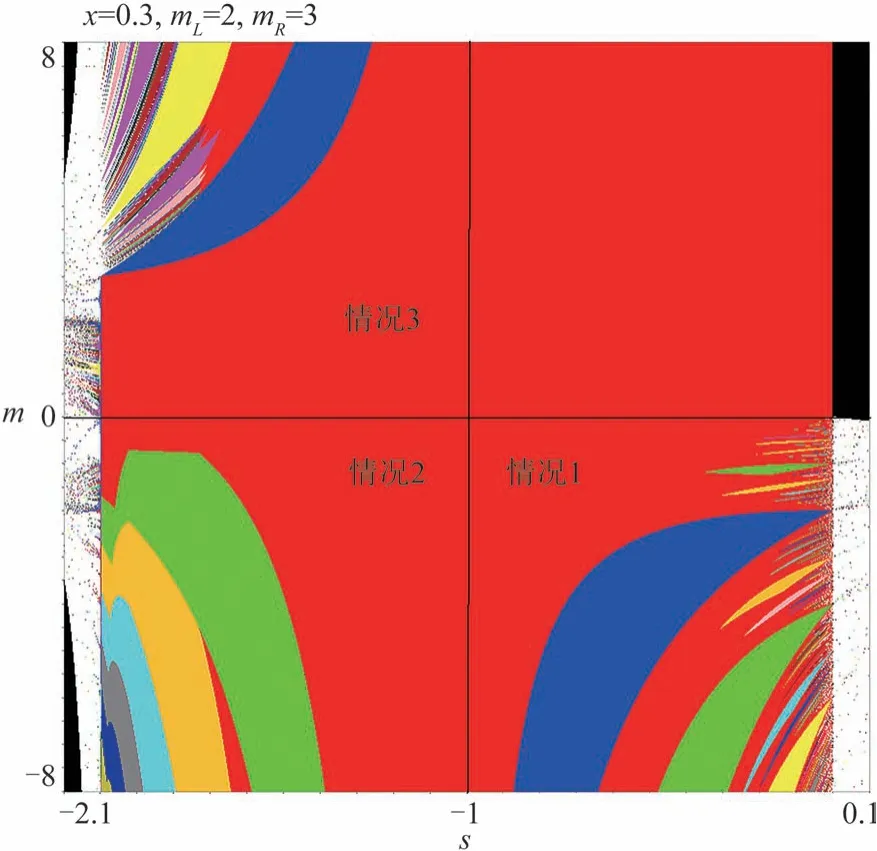
图1 全局二维分叉图Fig.1 Global diagramof two-dimensional bifurcation

下面针对3种情况，寻找周期区域中的周期环对应的符号序列，进而分别求解在参数平面(s，m)中界定这些周期区域的边界碰撞分叉曲线.

2 第一复杂度周期环的分叉曲线

本节将在参数平面(s，m)上确定周期吸引子存在区域、周期解边界碰撞分叉曲线.由（1）式可以计算出3个分支的不动点，分别为，只有当不动点在其定义域范围内，才称得上真实不动点，否则为虚拟不动点.在（2）式的假设条件下可知，xR始终是真实不动点，x L始终是虚拟不动点，对于中间分支不动点xC而言，当-1＜xC＜1时，xC是一个真实不动点，记为；否则为虚拟不动点记为特别的，若即不动点同不连续点发生接触，边界碰撞发生，因此m=±s是两条BCB曲线.

下面求解BCB曲线，首先必须寻找稳定的周期环，究其本质是研究迭代映射f n的不动点.显然，迭代映射f n依旧是分段线性映射，由对应的函数分支f L，f C和f R复合而成.本文将研究最简单的被称为第一复杂度的周期环，这种环的最大特点就是在一个分支上仅有一个周期点，而其他周期点在另外的分支上.本文将根据下面3种情况分析周期解和周期存在的区域：

情况1：-1＜s＜0，m＜0；

情况2：-2＜s＜-1，m＜0；

情况3：-2＜s＜-1，m＞0.

在情况1中，考虑到-1＜s＜0这一条件，所有线性函数的斜率都为正且小于1，可以断定此时所有的周期环（无论是否存在）都是吸引子.此时，由于，所以虚拟不动点位于右侧.由于m＜s＜0（事实上图1中情况1的部分位于过原点的直线m=s的右下方-1，虚拟不动点位于左侧.此时，位于左侧的点经过中间将被吸引到右侧，但是进入中间后又被吸引到左侧，最终在这时左侧和中间分支可能会形成稳定的周期.这类似于有一个非光滑点映射（不连续点为x=-1）的动力学行为.由于两个不动点均是虚拟的，且斜率为1+s＞0，如前所述，在左侧和中间分支形成符号序列为CLn的周期环，其周期区域的结构满足周期叠加结构.由于真实不动点是吸引子，从R侧出发的点经过有限次数的迭代，最终必将收敛到，因此，符号序列为CLn的周期与R侧的真实不动点共存于吸收区间中.

令符号序列为CLn的环的周期点为x0，当周期点x0与不连续点x=±1重合，计算出第一复杂度符号序列为CLn的周期环的边界碰撞曲线和，再求解：

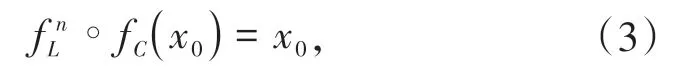
得到x0的表达式如下：

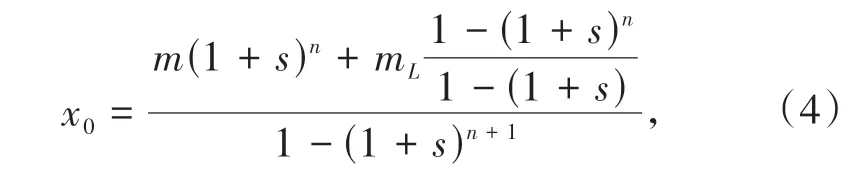
令x0=±1，可以求得参数空间(s，mL，m，mR)中的边界碰撞曲面：

情况2中，由假设条件知3个分支均递减，同时斜率都在-1和0之间，因此，所有的周期环（无论是否存在）都是吸引子.此时，会出现符号序列为C(LR)n的稳定的周期环.由假设m＜0＜1＜-s，当s＜m时，中间分支的不动点也是真实不动点.因此，s=m是不动点与关键点-1碰撞的BCB曲线.下面计算符号序列为C(LR)n的周期的边界碰撞曲线.类似于情况1的边界碰撞曲线的求解，只需要将（3）式中的f nL用(f R∘f L)n替换可得：

求解（5）式，得到中间分支的周期点：

中间分支周期点x0分别与1、-1以及-1的二阶像f R∘f L(-1)=(1+s)[-(1+s)+mL]+mR发生接触，进而得到以下3条分叉曲线和

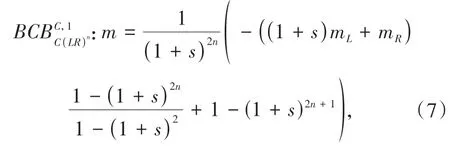
在情况3中，周期环以符号序列CR(LR)n为主.类似情况1和情况2中分叉曲线的计算，本文假设中间分支的周期点为x0，求解(f R∘f L)n∘f R∘f C(x)=x，得 到由中间分支分别与-1和-1的二阶像f R∘f L(-1)=-(1+s)2+(1+s)mL+mR发生接触，从而分别得到两条分叉曲线和

下文根据本节求解的边界碰撞分叉曲面，在（2）式的假设条件下，绘制参数平面(s，m)中的分叉曲线图，并结合对应的分叉图去分析其周期结构以及周期共存问题.

3 周期区域结构

对于本文模型的情况1，右侧分支不动点x*R始终是真实吸引子，由于周期环的构成只有中间和左边两个分支参与，因此，周期区域的结构与一个不连续点的情况没有本质区别.在一个不连续点的映射中，周期叠加结构的表示通常依赖于符号序列，例如，若p1和p2是不连续映射的两个不同的周期环，与之对应的符号序列分别为σ和ρ，假设它们的周期存在区域为∏(σ)和∏(ρ)，那么在σ和ρ两个环的存在区域之间存在着符号序列为σρ的周期区域∏(σρ)，在∏(σ)和∏(σρ)之间存在周期区域∏(σ2ρ)，一直重复下去，可以推断在任意两个周期区域之间存在无数个周期区域，相邻两个周期区域之间的周期为相邻两个周期的叠加，其符号序列是相邻两个周期符号序列的并置，并且满足Farey求和规则（Farey Composition Rule）.在情况1的条件下，符号序列分别为CLn和CLn+1的两个基本周期的周期区域之间一定有符号序列为CLn CLn+1的周期（第二复杂度的周期）区域.

图2（a）是图1中情况1部分的放大图，图2（b）是图2（a）的BCB分叉曲线和周期区域.从图2（a）可以观察到周期叠加的Farey求和规则.例如，在符号序列分别为CL2和CL3的周期存在区域中间，存在着符号序列为(CL2)m(CL3)n的周期区域.图2（b）中的周期区域中，以符号序列为CLn为例，其周期区域的上边界是中间分支周期点与不连续点1发生接触产生的边界碰撞分叉曲线其下边界对应的是中间分支周期点与不连续点-1发生接触产生的分叉曲线

图2 图1中情况1的局部放大图和BCB曲线图Fig.2 A partial enlargement and BCBcurves of case1 in Fig.1

图3为图1中情况2部分的放大，而图4参数空间(s，m)中的区域对应着一种新的周期增加机制，对应区域周期符号序列分别为C(LR)n和C(LR)n+1，其中n≥1.因为涉及到3个分支，所有区域的周期均是奇数并且相邻两个区域的周期递增2，因此，所有周期环均为Flip环（即特征值均在-1和0之间）.进一 步 可 以 观 察 到，Π(CLR)由和三条BCB曲线界定，Π(C(LR)2)由和三条BCB曲线界定，∏(C(LR)3)由和两条BCB曲线界定.由（2）式的假设条件，不动点始终为实的吸引子.∏(C(LR)2)和∏(C(LR)3)重叠区域（图4中蓝色区域）为五周期、七周期和实不动点共存区域，图4中红色区域是不动点、三周期和五周期共存区域，黄色区域是两实不动点、和三周期共存区域.

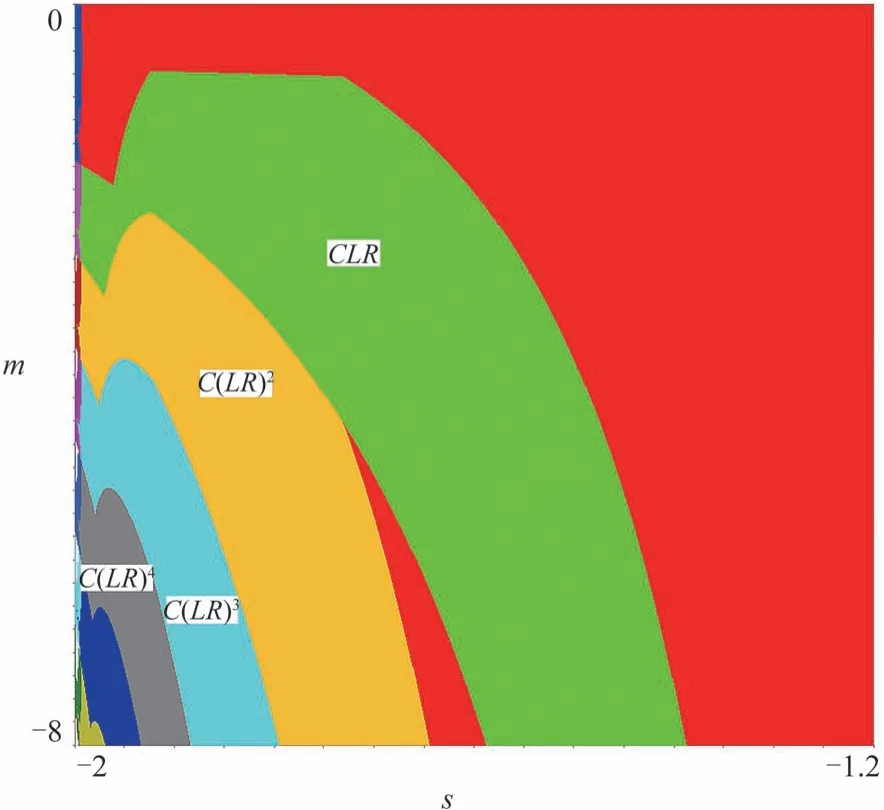
图3 图1中情况2的局部放大图Fig.3 A partial enlargement of case2 in Fig.1

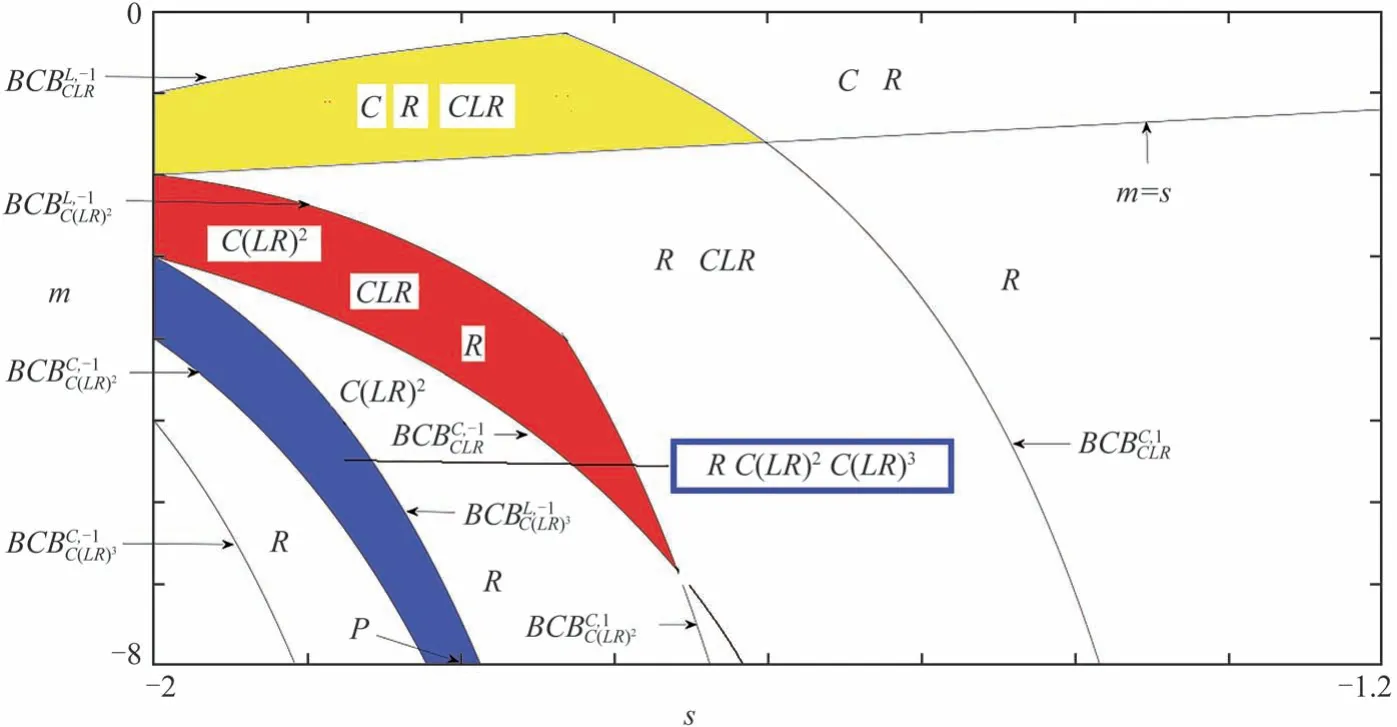
图4 图1中情况2的BCB曲线图Fig.4 Diagram of BCBcurves of case2 in Fig.1

在蓝色区域中，选取P点，即参数m=-8，s=-1.8.此时五周期C(LR)2、七周期C(LR)3和不动点三个吸引子共存于吸收区间I=[f C(1)，f L∘f C(1)]中.I=IR⋃IC，其中：

七周期和五周期共存于IC（位于图5中的黄色区域和浅蓝色区域），真实不动点x*R在区间IR（位于图5中的绿色区域）里.在区间I（图5中的黄色、绿色和浅蓝色区域）里，映射f是可逆的（严格单调递减），因此，映射f在区间I中并不会出现复杂的动力学行为，并且不变集只是稳定的周期环.基于f可逆这一性质，本文引入首次返回映射对模型的动力学行为进行解释.选取区间Jr=(-1，1)∈IC，其中不连续点记为是-1的前像，图4中P点的首次返回映射表达式如下：

图5 吸收区间图Fig.5 Diagram of absorbinginterval

因为映射f从区间IR出发的轨线最终收敛到吸引不动点，从其它地方出发的轨线经过有限次的迭代后必然经过区间Jr（图5中的黄色区域），首次返回映射Fr可以完全决定映射f在区间Jr中的动力学行为.图6是在参数m=-8，s=-1.8的时候，首次返回映射Fr（红色线段表示）和映射f（蓝色线段表示）的图像，结合公式（10），可知首次返回映射Fr与主对角线y=x的交点分别记为P1和P2，它们均是映射Fr的两个真实不动点，同时也分别是映射f的五周期和七周期位于中间分支的周期点.由公式（10）并且结合首次返回映射的定义，选取映射f初值在区间(-1，d)中，其路径必然为S1=CLRLR，而当初值选取在区间(d，1)中，其路径必然为S2=CLRLRLR，从中间分支（即区间Jr）出发以路径S1或S2回到中间分支，最终分别收敛到五周期和七周期.

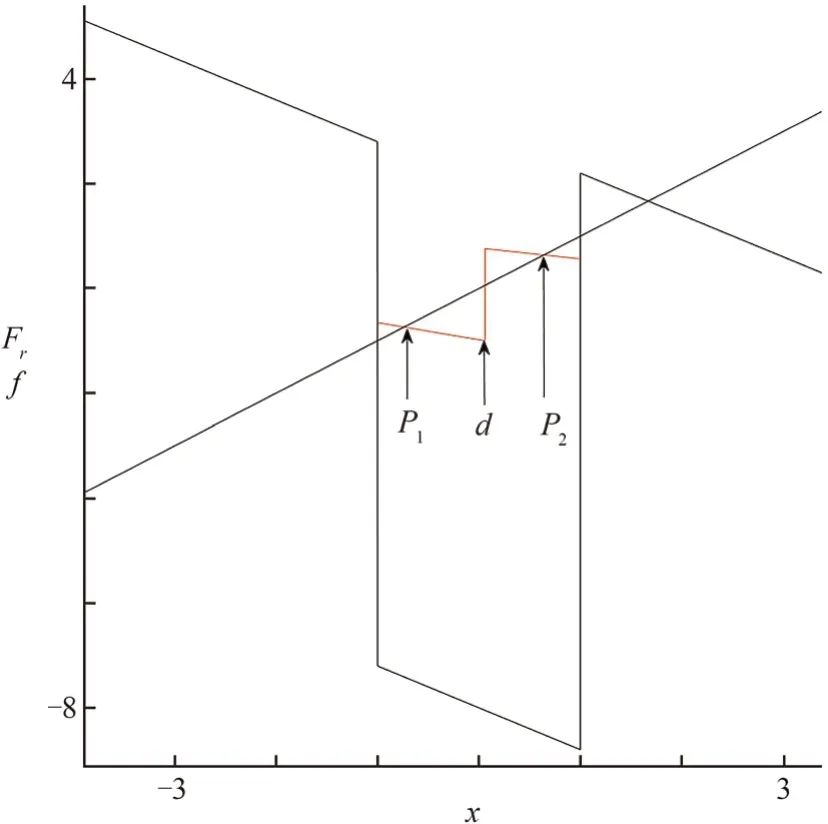
图6 首次返回映射图Fig.6 Diagramof thefirst return map

图7（a）为图1情况3部分的放大图，从中观察到，情况3以符号序列CL(LR)n的周期环为主.根据情况3的条件，所有的分支具有负斜率且所有的周期环都是稳定的.其周期增量为2，具有周期叠加性质，也就意味着，在符号序列分别为CR(LR)n和CR(LR)n+1的周期区域之间存在符号序列为(CR)2(LR)2n+1的周期区域.这是有两个非光滑点映射的特有性质，正如前所说，在只有一个非光滑点的映射中，两个分支不动点为虚拟时，只有在它们均为正则吸引不动点时（即两个分支斜率为正且小于1）才可能出现满足Farey规则的周期叠加现象.而对于有两个非光滑点的分段线性映射来说，由于涉及3个分支，虽然某个分支斜率为负，但是任意两分支的复合映射的斜率却为正，例如符号序列为CR和LR的二周期点分别为复合映射f R∘f C和f R∘f L的正则不动点，因此，符号序列分别为CR(LR)n和CR(LR)n+1的周期区域之间存在无限多个周期区域，其符号序列为两个相邻符号序列的并置，即满足Farey规则的周期叠加律.

图7 图1中情况3的局部放大图和BCB曲线图Fig.7 A partial enlargement and BCBcurves of case 3 in Fig.1

4 结语

本文对由资产价格模型简化假设得到的映射系统进行动力分析，固定两个参数mL=2，mR=3，在参数平面(s，m)中研究模型的周期区域结构.确定了边界碰撞分叉曲线，讨论了吸引周期区域的3种性质和不同结构.发现了多个不连续点映射的周期叠加结构的新情况.对于周期吸引子共存的问题，本文运用首次返回映射进行了解释.