基于局部轮廓曲线的图像配准方法

娄联堂，姚松

（中南民族大学 数学与统计学学院，武汉 430074）

图像配准是计算机视觉和图像处理应用中的一项基本任务.待配准的图像可以是在不同时间、从不同的视点、由不同类型的传感器捕获得到的.基于特征的图像配准目的旨在找到同一场景的参考图像f(x，y)与待配准图像f^(x^，y^)对应特征点的坐标变换［1］：

其中(x，y)T、(x^，y^)T分别表示参考图像、待配准图像的坐标，(b1，b2)T表示位移参数，A可以分解为：

其中θ1、θ2为旋转角度，λ1、λ2为尺度参数（本文用^表示与参考图像对应的待配准图像或参数）

本文利用图像中的局部轮廓特征研究图像配准问题，主要在最小作用曲面提取图像中的曲线特征的基础上，优化特征匹配与配准参数求解过程.具体地，在特征匹配阶段，对曲线的特征向量进行傅里叶变换以便使用轮盘匹配方法实现两幅图像中从角点出发的局部轮廓曲线的配准；在配准参数的求解过程中，从局部出发求解配准参数，然后根据局部参数的直方图确定全局坐标变换.

1 局部曲线及特征提取

给定图像f(x，y)，本文利用图像的最小作用曲面来提取图像中某点的局部曲线.对给定的起始点p0，最小作用曲面Up0(p)定义为点p0到p的路径积分的最小值［2］，即：

其中Ω∈Ap0，p，Ap0，p为p0到p的所有路径的集合，H是势函数，C(s)=(x(s)，y(s))代表二维图像f(x，y)上的曲线，s是曲线的弧长参数，ε为正则项.本文取势函数表示图像梯度幅值，δ为一个很小的正数.

为取得图像角点周围的轮廓曲线，选取图像的角点作为p0.由（3）式可知，满足以上条件的最小作用曲面其轮廓特征所在位置能量值一般小于周围非轮廓点的值，且距轮廓和p0位置越远的点其值越大.对于任一处于轮廓上的点p，使用快速行进（Fast Marching）算法［3］可以计算最小作用曲面Up0(p)，由此可以提取p0到任意一点p的轮廓曲线.

本文利用轮廓曲线来实现图像的配准，提取的曲线必须满足仿射不变性，为此，使用如下方法提取起始点为p0的轮廓曲线并进行排序：

（1）选择图像的角点为p0点；

（2）在图像中获取以p0为圆心，半径为r1和r2（r1＜r2）的圆环区域内的全部角点；

（3）使用快速行进算法提取p0到以上角点的最小作用路径，此路径即为起始点为p0的局部轮廓曲线；

（4）将起始点为p0的轮廓曲线按快速行进算法生成的顺序排序，即先生成的在前.

为了匹配两幅图像中角点的局部轮廓曲线，需要提取轮廓曲线的特征.XU［4］等使用曲线变形能量函数来描述曲线特征；XU［5］等提出曲线HAED特征描述符；WANG［6］等提出曲线MLSD特征描述符.前两者都是利用曲线的曲率进行特征描述，针对本文提取的局部轮廓曲线较短、变形信息少的特点，使用WANG等提出的MLSD特征描述符.

对曲线进行特征描述，首先要构造特征描述支撑区域，如图1所示［6］，对于图像上曲线C的像素点p，作一个以p为中心并与点p梯度方向d⊥和梯度逆时针正交方向dC对齐的矩形为支撑区域G1.将单个支撑区域G1划分为沿d⊥方向的非重叠子区域G11、G12、G13，然后将同一支撑区域内的像素梯度与d⊥、dC方向对齐，为其分配权重后按对齐的方向分别累加给该像素邻近的两个非重叠子区域构造单个支撑区域的特征向量.当曲线由w个像素构成时，曲线上所有支撑区域G1，…，Gw特征向量的均值和标准差组合即为MLSD特征描述符.

图1 曲线上点的子区域划分Fig.1 Subregion division of pointson acurve

2 基于轮盘的有序轮廓曲线的特征匹配

特征匹配方法是将参考图像与待配准图像中的特征向量逐一进行比较，将欧氏距离最近的一对特征向量视为匹配对.由轮廓曲线的提取方法知，轮廓曲线除满足仿射不变性外，同一角点的轮廓曲线是有序的.如果用一般的特征匹配方法来实现轮廓曲线的配准，会存在匹配的曲线不满足对应的位置关系.为此，本文提出轮盘的方法实现有序轮廓曲线的特征匹配.轮盘方法同时考虑特征向量之间的距离以及向量所对应曲线的位置关系进行匹配，能够减少位置不对应的误匹配.

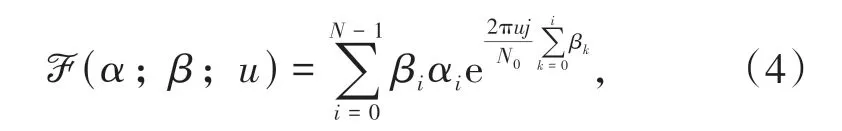
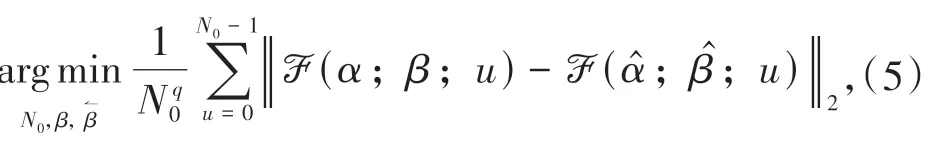
其中q≥1是N0的加权系数，当q越小，N0越接近2；当q越大，N0越接近min(N，).本文取q=3.

为获得两幅图像中角点与角点的局部轮廓曲线匹配关系，将参考图像f(x，y)角点轮廓曲线的特征向量序列逐一与待配准图像f^(x^，y^)角点轮廓曲线的特征向量序列按（5）式进行轮盘匹配.匹配误差越大，这一对角点局部轮廓曲线匹配的可能性越小.故设定阈值T，将不满足阈值要求的结果剔除，可得到匹配角点及对应轮廓曲线集合，其中是按（5）式的顺序进行了轮盘匹配的轮廓曲线.

3 基于局部到整体的配准参数求解

基于特征的图像配准方法中大多使用随机一致性（RANSAC）算法［7］，依赖全局匹配点求解配准参数，该算法在处理有较多异常值的数据时，收敛速度慢或无法找到收敛点［8］.为解决全局收敛性不好的问题，本文在配准参数求解时，首先依赖局部特征匹配结果点对和曲线集合的对应关系求解局部配准参数，然后根据局部参数的统计分布，获取全局配准参数.

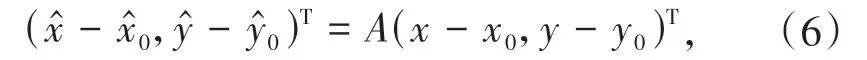
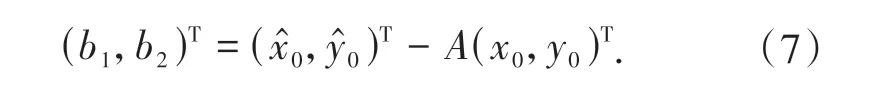
A的最小二乘解为：

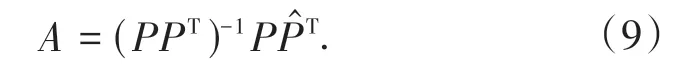
当N0＞2时，若存在pi、不满足位置对应关系，由此求出的配准参数的配准误差较大，故使用文献［9］的方法求解.设{p1，p2，…，pN0}所对应的拟合点为{p′1，p′2，…，p′N0}，其中：

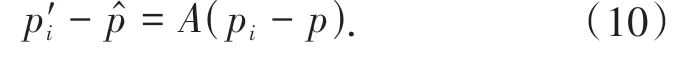
{p′1，p′2，…，p′N0}与的残差表示为：

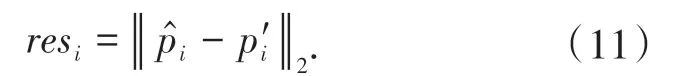
具有较大残差的拟合点很可能是接近正确匹配位置的点［9］，如图2拟合点位置始终比初始匹配点靠近正确匹配点.因此，可以找到残差大于res阈值的点，然后，将中对应的这些点替换为拟合点，替换后的点集为：

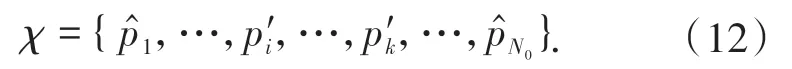
更新后的点集代入（8）式，依照（9）～（12）式的过程迭代求解，直到替换后的所有点残差均小于res阈值，最后一次迭代的矩阵A即为(p，^)的局部配准参数矩阵.由（2）式、（7）式得到(p，p^)的局部配准参数θ1、θ2、λ1、λ2、b1、b2.图2显示了点pi的错误匹配点在经过迭代后，对应的拟合点位置发生改变，最终与正确匹配点重合.

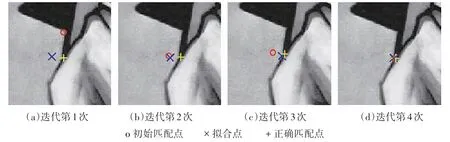
图2 迭代前后匹配点位置Fig.2 Matchingpoint position beforeand after iteration

在获取了局部配准参数后，本文利用局部配准参数θ1、θ2、λ1、λ2、b1、b2的统计分布来估计全局配准 参 数，各 参 数 的 取 值 范 围 为θ1、θ2∈[-π，π)，λ1、λ2∈(0，5)，b1、b2∈(-400，400).即作角点(p，p^)的局部配准参数直方图，其中直方图峰值的对应坐标可作为全局配准参数的估计值.

4 实验

4.1 算法流程

第1步：局部曲线及特征提取.

（1）计算图像f(x，y)、f^(x^，y^)的Harris角点［10］；

（2）利用快速行进算法计算以角点为圆心，半径r1=31，r2=63的圆环区域内全部角点的最小作用路径，获取局部轮廓曲线；

（3）使用MLSD描述符对曲线进行特征描述.

第2步：特征匹配.

将参考图像f(x，y)角点轮廓曲线的特征向量序列逐一与待配准图像f^(x^，y^)角点轮廓曲线的特征向量序列按（5）式进行轮盘匹配.设定阈值T=2，对大于阈值的结果进行剔除，得到匹配角点和对应轮廓曲线集合

第3步：局部到整体配准参数的求解.

（1）令res=1，取以及的另一端点代入（8）式进行（9）～（12）式的迭代，求出每一组(p，p^)的局部配准参数；

（2）统计局部配准参数θ1、θ2、λ1、λ2、b1、b2的直方图，每个直方图的间距为Δθ1=Δθ2=0.0618、Δλ1=Δλ2=0.021、Δb1=Δb2=4，其中直方图峰值的对应坐标可作为全局配准参数的估计值.

4.2 性能评价

采用均方根误差［11］（RMSE）来客观评价本文算法的准确性.均方根误差是一种衡量预测值与真实值之间偏差的方法，其值越小，配准方法越准确，表达式如下：

为进一步考察本文的配准算法，实验中将与JIANG［9］的C2F算法以及NNDR-RANSAC算法进行比较.本实验中选取两种配准算法共有的正确匹配点(xi，yi)比较均方根误差.

4.3 实验结果及分析

图3（a）为实验参考图像与待配准图像.图3（b）为图3（a）中两幅图像以对应角点为起始点提取的局部轮廓曲线.在固定半径的圆环区域内，分别提取了7条和10条局部轮廓曲线.图3（c）为图3（b）中曲线的特征向量序列轮盘匹配结果，两幅图像中共有4对曲线匹配（序号相同的即为匹配对）.不考虑局部路径差异的情况下，正确匹配的曲线有3对.其中b、d曲线存在局部路径差异，但并未影响其匹配结果.

图3 实验图像、局部轮廓曲线提取和轮盘匹配结果Fig.3 Experimental images，local contour curvesextraction and roulettematchingresults

图4为图3（a）中两幅图像的局部配准参数直方图.图中各参数的直方图均存在明显单峰值.图5为另一对实验图像及其局部配准参数直方图，图中各参数的直方图也均存在明显单峰值.由直方图得到的全局配准参数见表1.表2为C2F算法、NNDR-RANSAC算法和本文配准算法的均方根误差对比，图像3（a）中本文方法的RMSE值为2.1855，即实验匹配点与人工校准的匹配点之间的坐标误差在2.1855个像素单位，C2F算法和NNDR-RANSAC算法的对应值分别为3.2919、3.3545，在本组图像中本文配准方法准确度更高.图像5（a）（b）中3种方法的RMSE值分别为2.9693、1.9433和1.8114，其中NNDR-RANSAC算法与本文算法结果较为接近，C2F算法误差较大，准确性较低.

表1 全局配准参数Tab.1 Global registration parameters

表2 图像配准RMSE结果比较Tab.2 Comparison of RMSEresultsof imageregistration

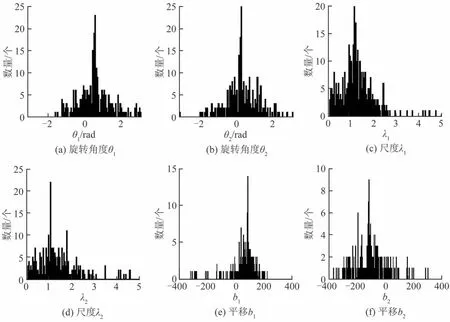
图4 局部参数直方图Fig.4 Histograms of local parameters

图5 另一对实验图像和局部参数直方图Fig.5 Other experimental imagesand histograms of local parameters

进一步分析，尽管提取到的轮廓曲线存在一些误差，但对其特征向量的匹配结果影响不大，由本文提取的特征结合轮盘匹配方法能够匹配多数对应曲线.通过配准后RMSE值的对比可知，本文配准方法与C2F算法、NNDR-RANSAC算法相比更有优势，能够得到更准确的配准参数.

5 结论

本文利用图像的局部轮廓曲线研究了图像配准问题.对参考图像与待配准图像从角点出发的局部轮廓曲线进行匹配，找到两幅图像中局部轮廓曲线的对应关系，然后由局部轮廓曲线的对应关系完成配准.通过实验对比分析了本文配准方法的效果，结果表明：本文配准方法有较高的配准精度.