网格与圆作图新题
2023-01-05天津南开日新学校张树义
⦿天津南开日新学校 耳 洁 张树义
在近几年的各地考试中有一种与网格和圆有关的作图题,这类题综合性强,层次高,能很好考查学生综合运用数学知识解决问题的能力.这类题常以压轴题出现,由于题型新,因此可参考的题目并不多.笔者新编了一些网格与圆相结合的作图题,给出题目的分析、解答和涉及的知识点,供大家教学时参考,不妥之处,恳请大家指正.
1 网格面积问题
“网格面积”类作图问题可涉及:作一个图形,其面积等于已知数值;作面积最大、最小的图形;把一个图形分成有一定要求的两部分;等等.

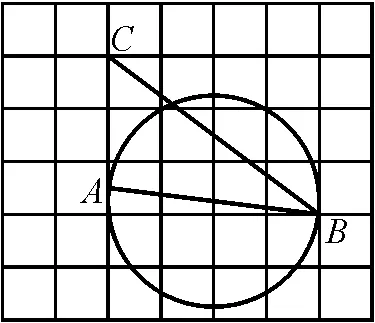
图1
分析:不难算出△ABC的面积为5,可知△ABP的面积是△ABC面积的一半,则考虑作△ABC的中位线与圆交于点P.
解:如图2,取格点D,E,连接DE交网格线于点F.取格点G,连接FG交AC于点H.设BC与网格线交于点M,作射线HM与圆交于点P,连接AP,BP,则点P即为所求.
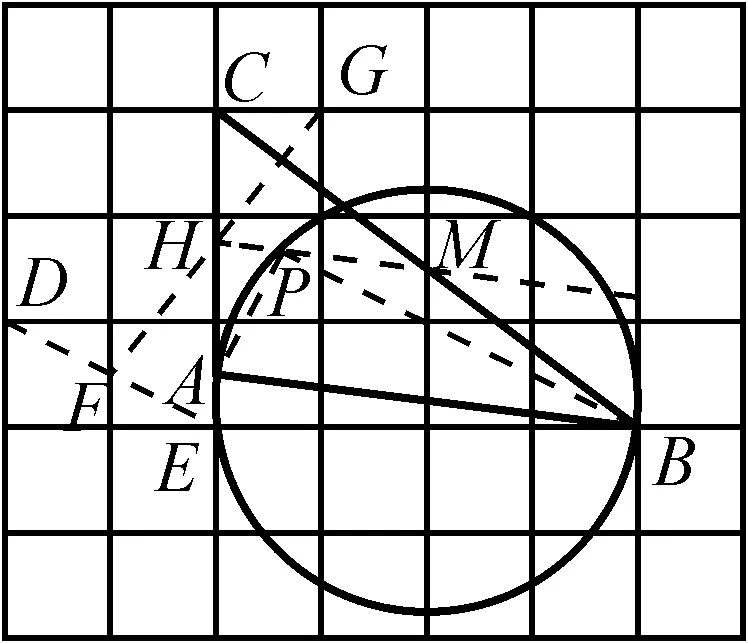
图2
涉及知识点: ①三角形中位线性质; ②平行线间的距离 ; ③网格作图基本动作——比例分线段.


图3

解:如图4,取格点C,D,连接CD交AB于点E.取格点F,G,H,N,连接FG,HN,两线段相交于点M.连接EM与圆交于点P,连接AP,BP,则点P即为所求.
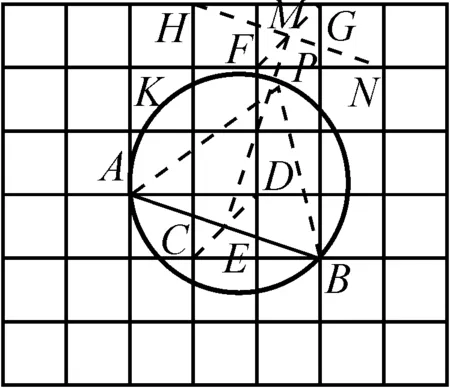
图4
涉及知识点:①垂径定理的推理; ②网格作图基本动作——比例分线段; ③网格作图基本动作——画已知线段的垂线.
2 网格角度问题
“网格角度”类作图问题可涉及:作一个角等于适当角度;平分已知角;作一个角等于一个角的几倍;平分弧;弧的倍分;等等.


图5
分析:如图6,延长线段AB至格点E,延长线段BA至格点F,则∠FAC=45°,故∠CAB=135°.所以作∠EAM=∠MAN=∠NAC=45°即可.

图6
解:如图6,取格点G,连接AG并延长交圆弧于点M.取格点H,连接AH并延长交圆弧于点N.点M,N即为所求.
涉及知识点: ①圆周角定理的推论;②等腰直角三角形的判定与性质;③网格作图基本动作——画指定大小的角或作角的平分线.
3 网格线段问题
“网格线段”类作图问题可涉及:作两条线段相等;找圆心;作切线;将军饮马问题;胡不归问题;阿氏圆问题;作最长、最短的线段;等等.

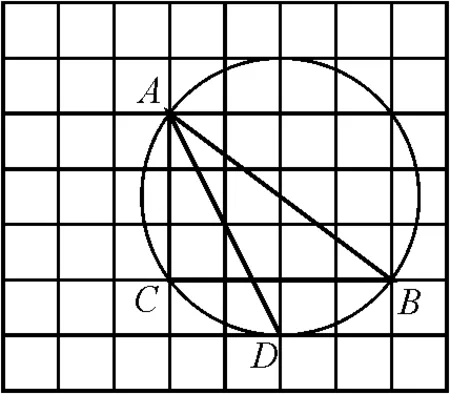
图7

解:如图8,取格点H,G,连接GH交AB于点M.取格点N,连接NH交AC于点F,连接MF交AD于点E.点E,F即为所求.

图8
涉及知识点:①圆周角定理的推论;②全等三角形的判定与性质;③最短路径问题,即垂线段最短;④网格作图基本动作——比例分线段;⑤网格作图基本动作——画已知线的垂线(或平行线).

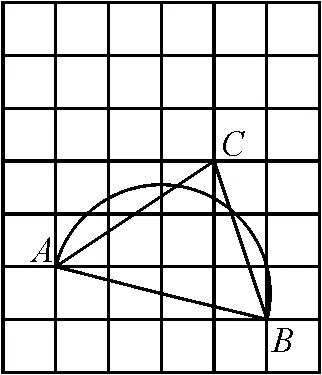
图9

解:如图10,取格点D,连接CD交网格线于点E.连接AE交半圆于点F.连接BF交AC于点P,点P即为所求.

图10
涉及知识点:①最值,即胡不归问题;②相似三角形的判定和性质;③网格作图基本动作——画已知线的垂线(构造等腰直角三角形);④网格作图基本动作——比例分线段.
例6如图11,将△ABC放在每个小正方形边长为1的网格中,点A,B,C均落在格点上,动点P到点A的距离为2,点Q是线段BP的中点,连接线段CQ,当线段CQ最小时,在图中用无刻度的直尺画出点P和点Q,并简要说明画法.

图11

解:如图12,取格点D,连接AD.取格点E,F,连接EF交AD于点P.连接BP,取格点K,连接CK交BP于点Q.点P,Q即为所求.

图12
涉及知识点:①最值,即隐圆问题;②三角形中位线性质;③网格作图基本动作——比例分线段.
4 作图思路总结
结合以上六个例题,汇总常见作图的思路:
(1)通过圆周角90°确定直径;
(2)通过两直径确定圆心;
(3)通过等弧所对圆周角相等确定角平分线;
(4)通过直径确定圆周角90°(即两直线垂直关系);
(5)通过隐圆确定动线段的最短、最长线段.
5 结束语
网格作图问题承载着几何直观能力、逻辑推理与合情推理能力、运算能力、应用意识、创新意识等学科核心素养的落地体现,同时,蕴涵着转化、化归、数形结合、数学建模等数学思想,是中考命题的热点之一.以往网格作图问题通常依托于全等、相似、线与线的相对位置、三角形或四边形的基本性质,让学生利用网格作垂直、平行,构造相似与全等,将线段n等分[1].而今试题增加了圆这一背景后,增加了知识的综合性,使试题更灵活,借助圆心、半径、直径、圆心角、圆周角、切线等的基本性质,作图更便捷,思维更广阔,既能考查学生综合解决问题的能力,又能呈现出更加美观的作图效果.利用网格与圆相关性质的结合还可以解决更多几何变换中旋转、翻折等典型问题.
