基于变量选择的尖点突变模型的两步构建方法
2023-01-05付冬梅程学群杨丙坤郝文魁邵立珍
张 明,付冬梅,程学群,杨丙坤,郝文魁,陈 云,邵立珍
1) 北京科技大学顺德研究生院,佛山 528300 2) 北京科技大学自动化学院,北京 100083 3) 北京科技大学北京市工业波谱成像工程技术研究中心,北京 100083 4) 北京科技大学新材料技术研究院,北京 100083 5) 北京科技大学国家材料腐蚀与防护科学数据中心,北京100083 6) 全球能源互联网研究院有限公司先进输电技术国家重点实验室,北京 102209
在复杂的系统中,外界因素的变化可能会导致系统状态的跳跃式变化,称为突变.Qiao 等[1]认为深埋隧道围岩的失稳是一种突变现象,给矿井的安全生产带来极大威胁,并通过分析得出围岩失稳发生在第3 至4 步开挖过程中.Zhi 等[2]通过分析得到使腐蚀速率急剧变化的环境变量的阈值,当环境变量超过该阈值时,腐蚀速率会发生突变.裴甲坤等[3]认为化工事故是由危险源和不安全因素引起的突发事件,二者的综合影响导致系统的安全状态发生突变.其他诸如股市崩盘[4-5]、人的心理状态变化[6]、电力系统故障[7]等也属于突变现象.此类现象包含复杂的系统行为,既有连续性变化又有突发的不连续性变化,且影响因素往往众多,给实际工程问题的建模和解释带来困难.
对于小样本工程数据,线性模型、灰色模型[8]是常用的方法;对于大样本工程数据,人工神经网络[9]、随机森林(Random forest,RF)[10]等机器学习模型通常可以获得较好的建模效果.虽然机器学习模型具有强大的非线性映射能力,但无法解释研究对象的突变现象.突变理论是用以解释复杂系统中不连续性和质变现象的数学理论,由法国数学家Thom[11]提出.假定一个系统的动力学方程可以由一个光滑的势函数导出,根据控制因子和状态因子个数的不同,Thom 定义了7 种基本的突变模型,并推导出每一种模型势函数的解析形式.由于形式简单、直观,具有两个控制因子和一个状态因子的尖点突变模型应用最为广泛,模型参数的估计可由Cobb 提出的极大似然估计法(Maximum likelihood estimation,MLE)实现[12-13].作为解决工程领域中不连续性复杂问题的一种数学工具,突变理论在经济学、生物学、物理学、心理学等领域应用广泛.
在以往的尖点突变模型中,组成控制因子的输入变量往往依据经验或已有的结论来确定.如,文献[4-5]基于Zeeman[14]的理论基础,将股票市场中基本面交易者和技术分析交易者的多维数据作为输入变量构建股票市场的尖点突变模型.这种建模方式受限于特定学科,不利于推广,且输入变量的实际价值难以判断.在待选的输入变量较多且突变机理不明确的情况下,如何利用少量的重要变量构建尖点突变模型依然是一个难点.常见的变量选择方法分为过滤法、嵌入法、封装法.其中,过滤法依据待选变量统计特性的各项指标来选择重要变量,如皮尔逊相关系数法、方差过滤法;嵌入法依据机器学习算法本身来分析待选变量的重要性,如RF 的排列变量重要性算法[10,15];封装法基于构造的最终模型来选择使模型性能达到最优的变量子集,最终模型可以是支持向量机(Support vector regression,SVR)[16]、梯度提升回归树(Gradient boosted regression trees,GBRT)[17]等机器学习算法.过滤法的评价标准独立于特定的学习算法,具有较好的通用性,但难以取得很好的建模效果;嵌入法、封装法虽然可以取得较好的建模效果,但是这种基于单一模型的变量选择算法存在特定的偏差,变量子集的选取依赖于特定模型,容易产生过拟合现象.采用集成方法,即通过组合不同方法的变量选择结果来产生变量子集,既减轻了对特定模型的依赖性,又可以很好地提高结果的准确性和稳定性[18-20].
针对传统尖点突变模型依据经验建模的问题,提出基于变量选择的尖点突变模型的两步构建方法.该方法的通用性较强,可广泛应用于具有突变特征的系统的建模并能得到模型的数学解析式.建模过程分为两步.第一步,以RF、GBRT、SVR 作为基学习器,利用多模型集成重要变量选择算法(Multi-model ensemble important variable selection,MEIVS)来量化待选变量的重要性,提取得分之和超过总分90%的前n个待选变量作为后续建模的输入变量;第二步,基于MLE 算法构建尖点突变模型.本文首先介绍了尖点突变模型的原理、数据拟合方法以及突变特征,其次介绍了MEIVS 算法的实现流程,最后结合工程实例,验证了该方法的有效性.
1 基本原理
1.1 尖点突变模型与突变特征
1.1.1 尖点突变模型
突变理论描述了动力学系统中控制因子和状态因子之间的关系,在控制因子固定的情况下,系统始终寻求平衡状态,直到达到势函数的极小值或极大值为止.以动力学系统表达式来描述系统的状态因子z在控制因子a的影响下随时间t的变化:
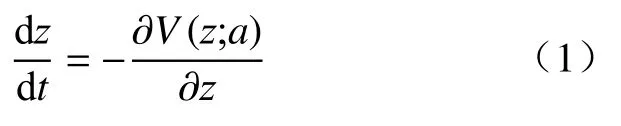
V(z;a)是系统的势函数.应用最广泛的尖点突变模型由2 个控制因子α、β和一个状态因子z组成,其势函数的规范形式是:
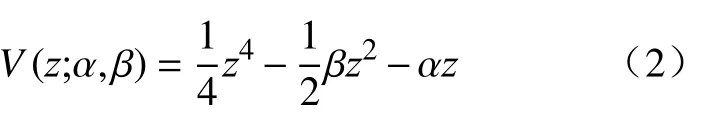
系统的平衡方程由(3)式确定,在无扰动的情况下,系统的状态不随时间变化:
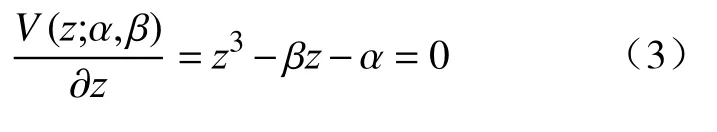
当平衡点的势函数V(z;α,β)是关于z的极小值时,平衡点是稳定的,系统即使受到扰动的影响,也会随着时间t回到稳定状态;当平衡点的势函数V(z;α,β)是关于z的极大值时,平衡点是不稳定的,系统在扰动的影响下会偏离此平衡点,从而被稳定的平衡点吸引.在不同的α和β值下系统平衡点的数目和性质可以由Cardan 判别式δ判断,表示为:

当δ>0 时,存在一个稳定的平衡点;当δ<0 时,存在两个稳定的平衡点和一个不稳定的平衡点;当δ=0 时,存在一个稳定的平衡点和一个不稳定的平衡点.图1 给出了由平衡点的集合构成的平衡曲面和由控制因子构成的控制平面.平衡曲面的形状像一个有“褶皱”的连续曲面,并且由上叶、中叶、下叶3 部分构成,上叶和下叶部分对应的平衡点是稳定的,中叶部分对应的平衡点是不稳定的.控制平面是平衡曲面在z轴方向上的投影,中叶区域在控制平面上的投影称为尖点突变模型的分叉集.图1 中,若控制因子α、β沿红色轨迹A 变化,状态因子z会在分叉集内发生突变,从平衡曲面的下叶直接跳变到上叶而不经过中叶;若控制因子α、β沿蓝色轨迹B 变化,则状态因子z不会发生突变.
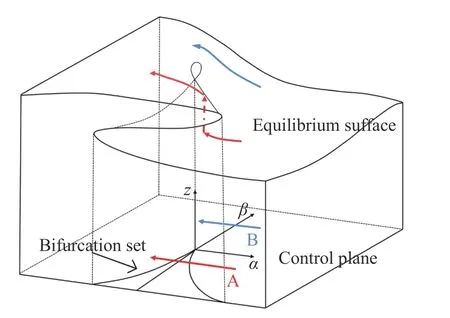
图1 尖点突变模型的平衡曲面和控制平面Fig.1 Equilibrium surface and control plane of the cusp catastrophe model
在实际应用中,数据难免受到随机噪声影响,Cobb 和Zacks[12-13]通过引入随机微分方程,以概率密度函数的形式描述了系统在α、β固定的条件下z的分布,表示为:
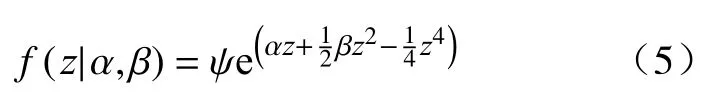
式中,ψ是归一化常数,α、β分别为n维输入变量{X1,···,Xn}的线性组合,z为输出变量Y的线性变换,表示为:

参数θ={w0,w1,a0,···,an,b0,···,bn}由MLE 方法估计.在给定N个观测样本的情况下,参数θ的对数似然函数如下:
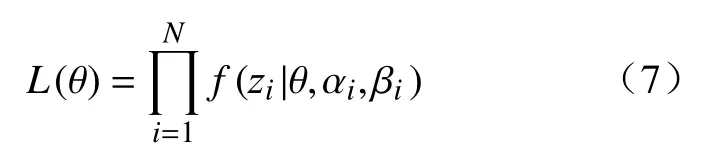
最大化观测样本的对数似然函数得到参数θ的估计值,优化搜索算法为带边界约束的Broyden-Fletcher-Goldfarb-Shanno 算法:
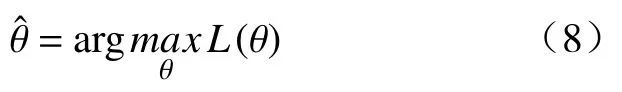
1.1.2 评价指标
为了验证尖点突变模型的性能,将线性模型和非线性的Logistic 模型与尖点突变模型作对比[21].其中,Logistic 模型可以模拟研究对象的急剧变化,但没有考虑不连续性变化.评价指标采用可决系数,R2、赤池信息准则(Akaike information criterion,AIC)和贝叶斯信息准则(Bayesian information criterion,BIC).当R2越大时,模型的精度越高;AIC 和BIC 考虑了模型复杂度,当AIC 和BIC 越小时,模型越好.
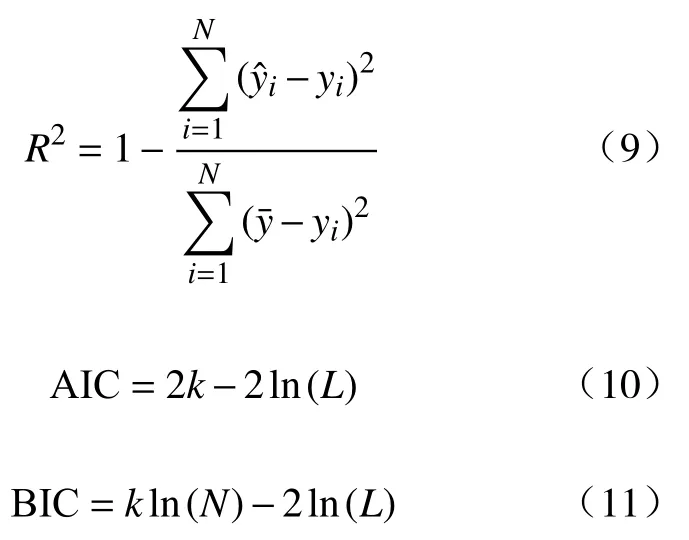
1.1.3 突变特征
在系统的势函数未知的情况下,常常根据系统表现的外部性态来判断系统是否存在突变,这些性态被称为突变特征[14,21].尖点突变有5 个特征:(1)多模态:系统中可能出现两个不同的状态;(2)不可达性:系统存在不稳定的平衡态;(3)突跳:系统从一个势函数极小值跳到另一个极小值;(4)发散:控制因子的微小变化可以导致状态因子的质变;(5)滞后:当物理过程可逆时,发生突变时对应的控制参数位置可能不同.当系统存在突变现象时,对外往往表现为其中的一个或几个的组合.在实际应用中,针对截面数据,应首先检查研究对象概率密度的双峰性,双峰性意味着系统可能存在多个状态;针对时序数据,则应首先检查时间序列中的跳变现象[21].
1.2 多模型集成重要变量选择算法
而在传统的尖点突变模型的建模过程中,输入变量的选取往往依赖于已有的实践或经验,这与目前数据规模的爆发式增长相矛盾,不利于尖点突变模型的普及应用.为了解决上述问题,同时提高模型的精度、降低模型的复杂度,本文基于排列[23]的思想提出MEIVS 算法.
排列的思想借鉴于随机森林的变量重要性度量方法,认为模型会更依赖于重要的输入变量做预测.当打乱某一变量在测试集上的观测序列后,用新生成的数据做预测,更重要的输入变量会使模型的精度损失更大.MEIVS 算法组合了RF、GBRT、SVR 3 种常用的机器学习算法,其中RF 和GBRT 都属于决策树的集成学习算法,但它们采用的计算策略不同;SVR 采用高斯核函数.文献[24-26]中对每种方法的机理都作了解释.本文的损失函数采用的是均方根误差(Root mean squared error,RMSE):
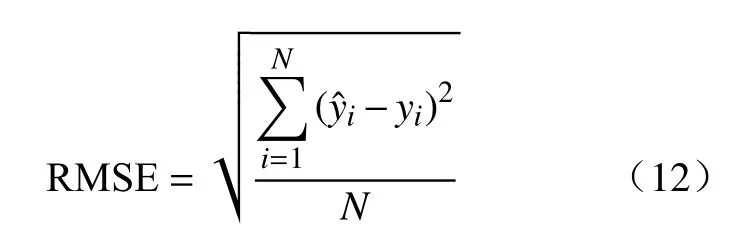
以样本的80%作为训练集,20%作为测试集,使用Z-Score 标准化方法对输入变量进行处理,经过处理的数据的均值为0,标准差为1.记m个待选变量的集合为{S1,···,Sm},目标是得到n个重要变量的集合{X1,···,Xn}作为尖点突变模型的输入变量.算法步骤如下,流程图如图2 所示.
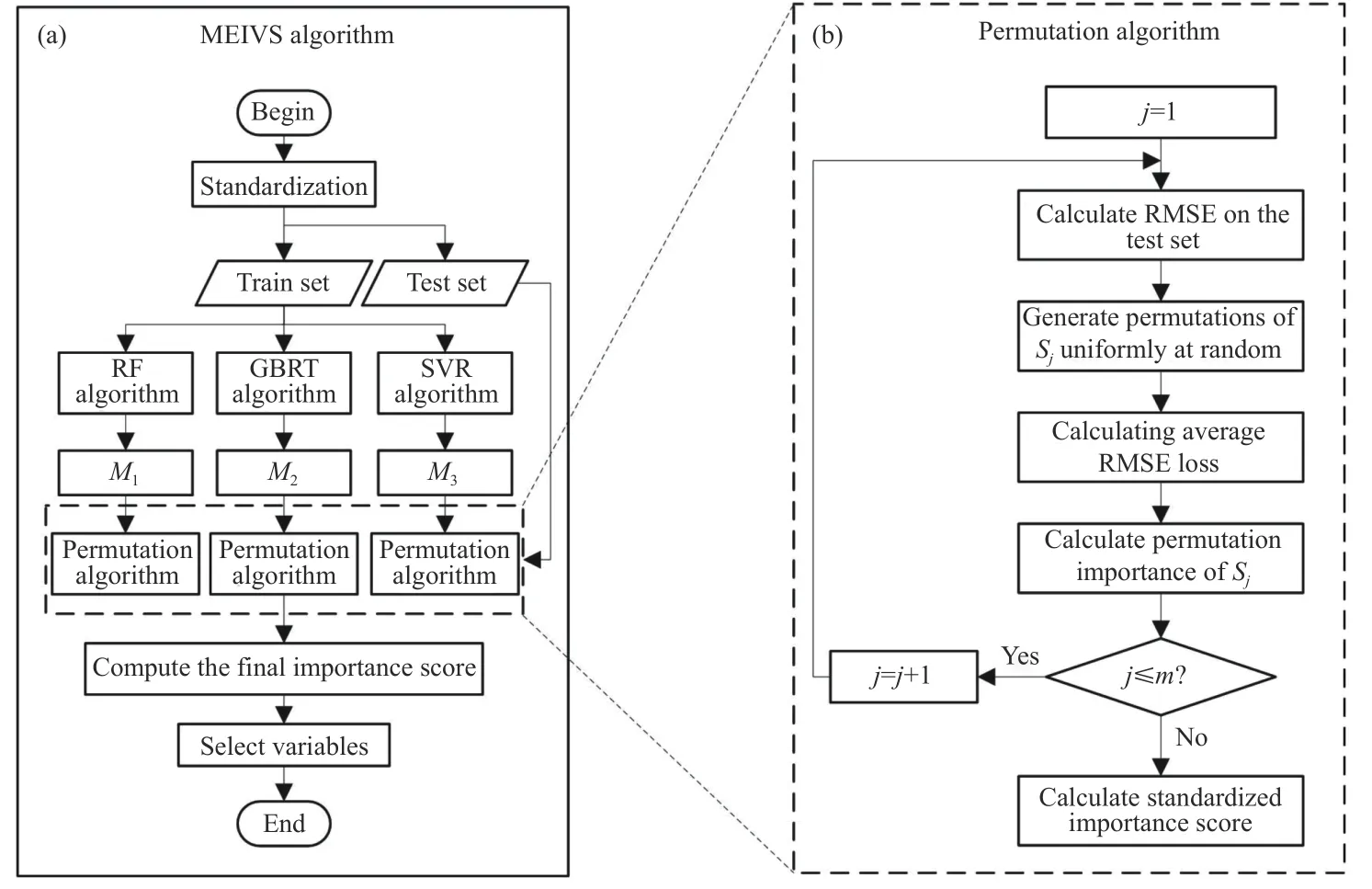
图2 MEIVS 算法流程图.(a) MEIVS 算法主流程;(b) 排列算法流程Fig.2 MEIVS algorithm flowchart: (a) main process steps of the MEIVS algorithm;(b) process steps of the permutation algorithm
步骤1 利用训练集训练RF、GBRT、SVR 模型,记为M1、M2、M3,对于所建立的每个模型Mi,分别基于置换算法计算变量重要性,即执行步骤2、步骤3;
步骤2 计算模型Mi在测试集上的均方根误差并记为,对{S1,···,Sm},依次执行(1)~(3):
(1) 打乱Sj在测试集上的观测序列并重新计算模型的均方根误差,由于涉及随机性,此过程重复10 次,分别记为
(2) 计算Sj在测试集上的平均预测精度损失:
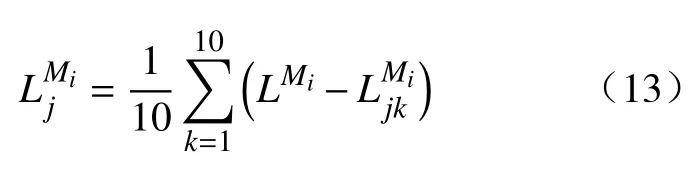
(3) 计算Sj在模型Mi上的排列重要性得分,当时,将重要性得分记为0,该变量无用:
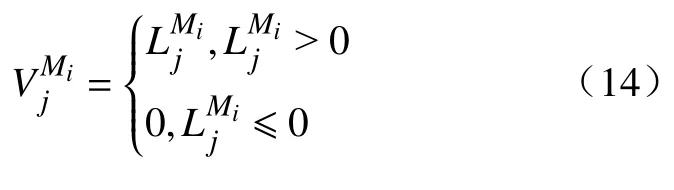
步骤3 计算Sj的标准化排列重要性得分:
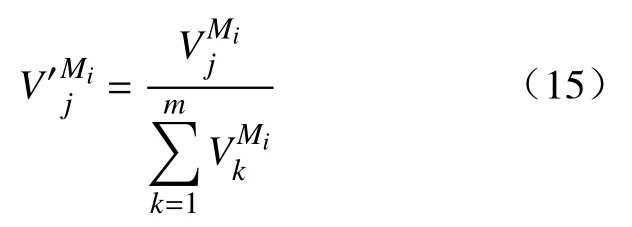
步骤4 计算Sj在M1、M2、M3上的重要性总得分:
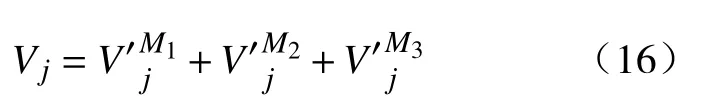
步骤5 按变量重要性得分{V1,···,Vn}降序排列待选变量{S1,···,Sm},提取得分之和超过总分90%的前n个待选变量作为重要变量,记为{X1,···,Xn}.
1.3 基于变量选择的尖点突变模型的两步构建方法
将MEIVS 方法与基于MLE 的尖点突变模型参数估计方法相结合,分两步构建尖点突变模型.第一步,利用MEIVS 来量化待选变量{S1,···,Sm}的重要性,提取重要变量{X1,···,Xn};第二步,利用提取的n个重要变量,基于MLE 算法构建尖点突变模型.
2 仿真结果和分析
以两个不同领域的、具有突变特征的数据集为例,验证了所提方法的有效性.其中,欧洲旅馆住宿价格数据集[27]为截面数据集,来源于Kaggle平台;北京大气腐蚀数据集为时序数据集,来源于北京地区的大气暴露实验.
2.1 在截面数据集上的应用—以欧洲旅馆住宿价格数据集为例
Kaggle 平台的欧洲旅馆住宿价格数据集一共包含120 个样本,每个样本包括每日住宿价格(Price)、星级(Star)、离市中心距离(Distance)、评分(Rating)、房间数目(Room)、房间面积(Square)和所在城市(City).Price 为输出变量,单位为每日花费的可兑换马克(KM·d-1),其余为输入变量,其中类别变量City 以Price 的类别均值来编码.Price 概率密度的非参数估计如图3,非参估计的核函数选用高斯核,带宽设置为25,概率密度的双峰性暗示了Price 可能会发生突变,因此适用于建立尖点突变模型.两步构建方法中第一步为提取重要变量.利用MEIVS 得到各个待选变量的重要性得分,如图4.条形图中横轴表示影响每日住宿价格的待选变量,纵轴表示每个待选变量的重要性总得分,每个待选变量在各模型上的得分以不同的颜色区分,并且根据得分降序排列.依据MEIVS 算法中步骤(5),Square、Rating、Star 和Room 为重要变量,设为X1、X2、X3、X4,每日住宿价格Price 设为Y.算法基于R 语言中的DALEX 程序包[28]实现.
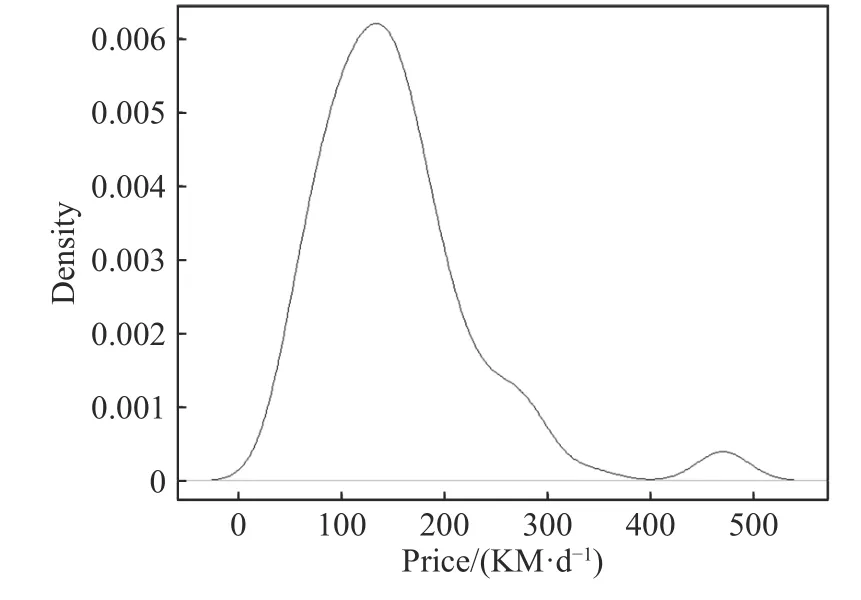
图3 每日住宿价格的概率密度非参数估计Fig.3 Nonparametric estimation of the probability density of the daily accommodation price

图4 欧洲旅馆住宿价格数据集待选变量重要性得分Fig.4 Importance score of the variables to be selected in the European hotel accommodation price dataset
将MEIVS 提取的重要变量X1、X2、X3、X4作为输入变量、每日住宿价格Y作为输出变量建立尖点突变模型,为了消除变量间量纲的影响,用ZScore 标准化方法对原始输入变量进行处理.算法基于R 语言Cusp 程序包[22]实现.利用MLE 算法和120 条样本对参数θ={w0,w1,a0,a1,a2,a3,a4,b0,b1,b2,b3,b4}进行估计,代入式(6)中,得到如下形式的尖点突变模型的平衡方程:
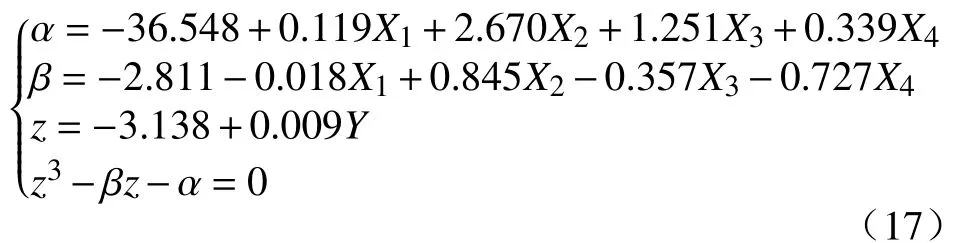
表1 展示了采用两步构建法建立的尖点突变模型与经MEIVS 降维后构建的线性模型、Logistic 模型的评价指标,同时与传统的直接建模方法、经斯皮尔曼相关系数(Spearman's correlation coefficient,SCC)、最大互信息系数(Maximal information coefficient,MIC)、随机森林变量重要性算法(Random forest variable importance measure,RFVIM)降维的建模方法作比较.其中,SCC 和MIC 剔除系数小于0.3 的弱相关变量,RFVIM 提取累计变量重要性达到90%的前n个变量.结果显示,在考虑样本量的情况下,更高的R2和更低的BIC 说明基于两步构建法所构建的尖点突变模型优于未降维的传统尖点突变模型以及经SCC、MIC、RFVIM降维后所构建的尖点突变模型.
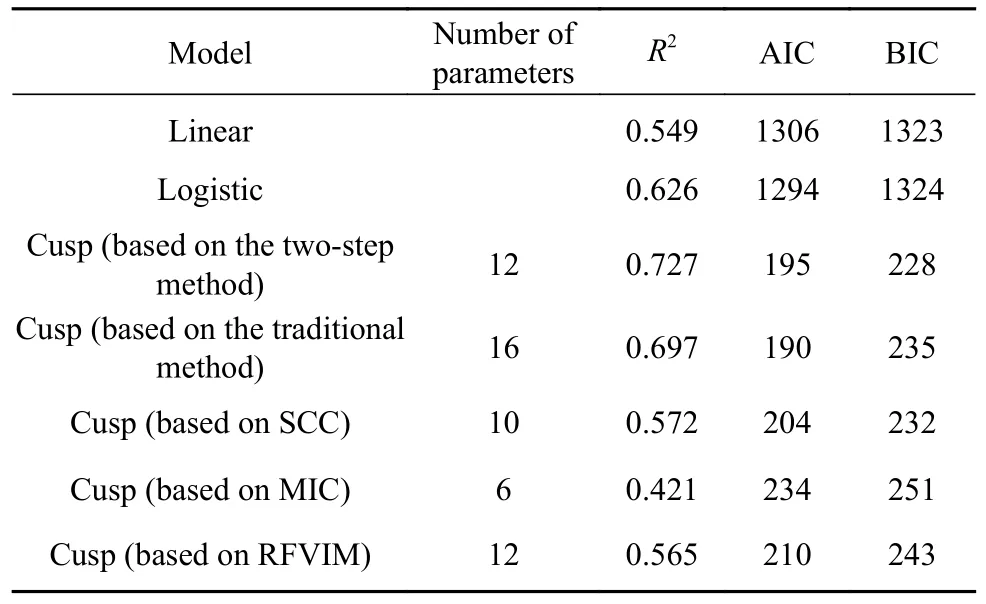
表1欧洲旅馆住宿价格数据集建模结果评价Table 1 Evaluation of the modeling results of the European hotel accommodation price dataset
图5(a)展示了样本在控制平面上的分布,其中散点的颜色代表经过式(6)线性变换后旅馆价格的数值大小.影响旅馆价格的控制因子的变化轨迹从左到右穿过了分叉集,表明旅馆的价格发生了突变.图5(b)展示了样本在平衡曲面上的分布,平衡曲面设置为半透明状态,颜色较暗的散点位于平衡曲面下方.易观察到在较低的价格范围内旅馆价格的变化具有连续性,而从低价到高价的变化并不连续.
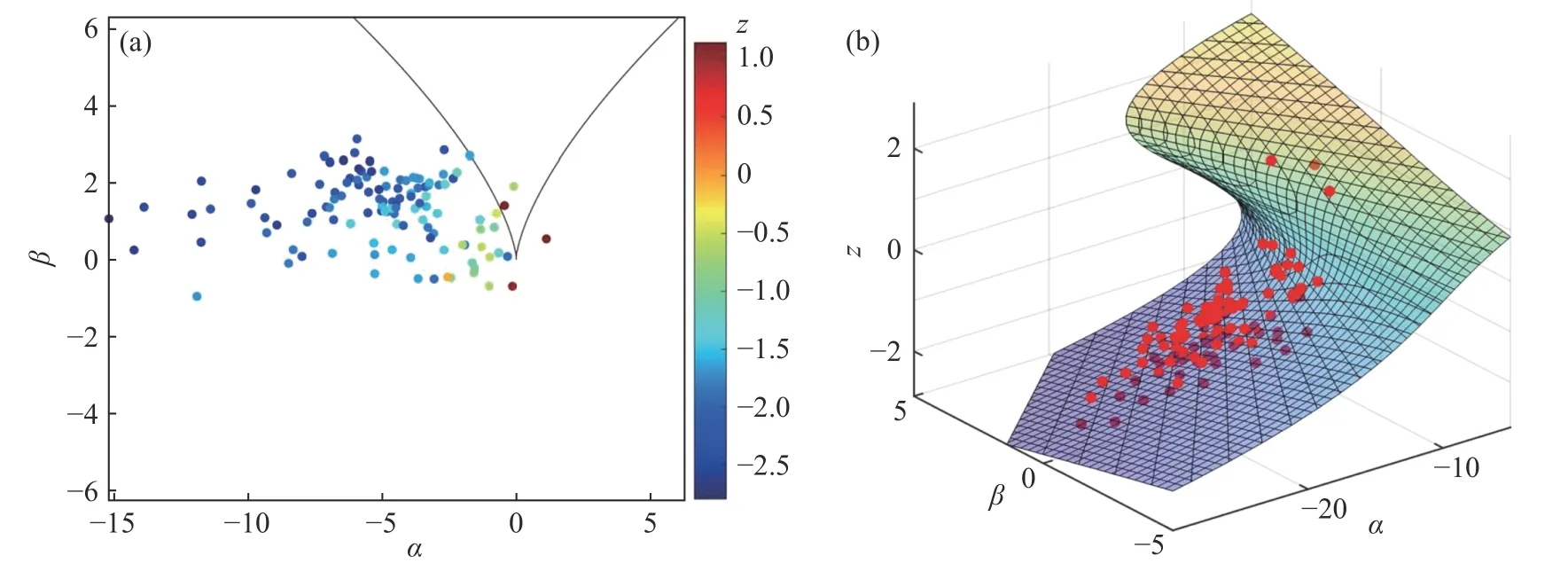
图5 欧洲旅馆住宿价格数据在控制平面 (a) 和平衡曲面(b) 上的分布Fig.5 Distribution of the European hotel accommodation price dataset on the control plane (a) and equilibrium surface (b)
2.2 在时序数据集上的应用—以北京大气腐蚀数据为例
北京大气腐蚀数据集一共包含719 个样本,采集时 间为2018 年8 月5 日16 时至9 月6 日14 时,采集地点为北京,每个样本包括大气腐蚀监测仪(Atmospheric corrosion monitor,ACM)采集得到的早期大气腐蚀电偶电流(Galvanic current)、温度(T)、相对湿度(RH)、降雨状态(Rainfall)以及大气环境中PM2.5、PM10、SO2、NO2、O3的浓度.电偶电流与腐蚀速率成正相关关系[29],为了便于分析,取电偶电流的自然对数作为输出变量.图6 展示了电偶电流的时间序列表明腐蚀电偶电流波动较大,表明时间序列中具有突变的特性,因此适用于建立尖点突变模型.
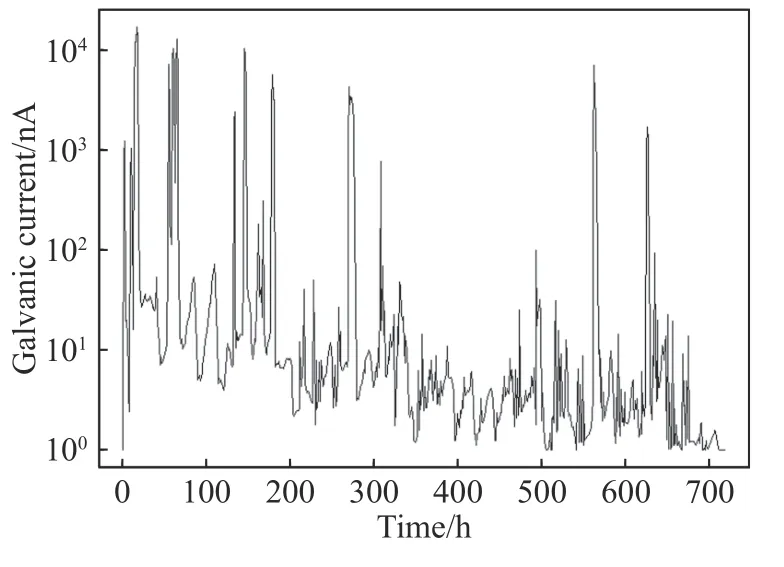
图6 ACM 采集到的电偶电流时间序列Fig.6 Time series of the galvanic current collected by ACM
通过MEIVS 算法得到待选变量重要性得分如图7,可见T、RH 和Rainfall 为影响早期大气腐蚀的重要变量,设为X1、X2、X3,对数化腐蚀电偶电流设为Y.其他污染物浓度的影响是微弱的.
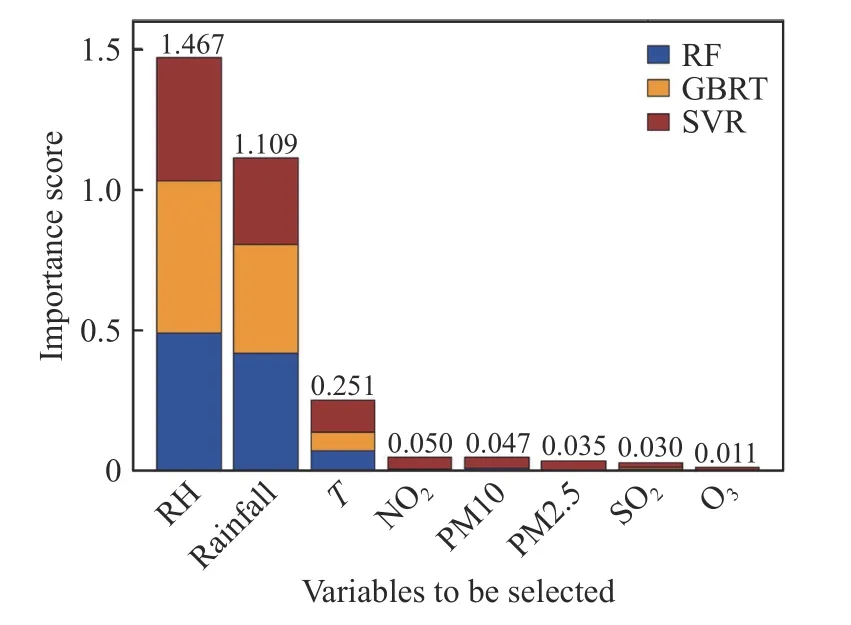
图7 北京大气腐蚀数据集待选变量重要性得分Fig.7 Importance score of the variables to be selected in the Beijing atmospheric corrosion dataset
以Z-Score 标准化后的X1、X2、X3作为输入变量、Y作为输出变量构建尖点突变模型,利用MLE算法和719 条样本对参数θ={w0,w1,a0,a1,a2,a3,b0,b1,b2,b3}进行估计,得到的平衡方程如下:
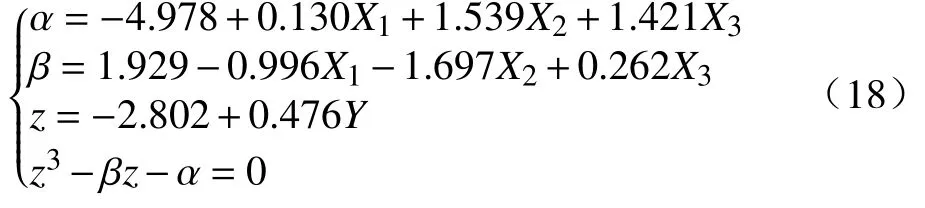
此外,采用上文所述方法,表2 的模型评估结果显示了两步构建法的优越性.
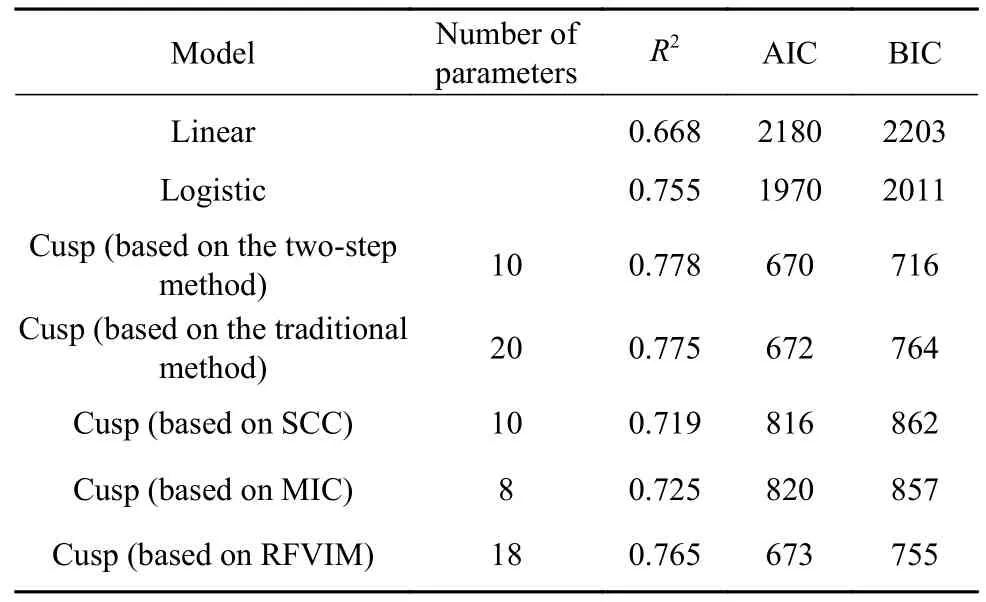
表2 北京大气腐蚀数据集建模结果评价Table 2 Evaluation of the modeling results of the Beijing atmospheric corrosion dataset
样本在控制平面和平衡曲面的分布情况如图8(a)、8(b),圆点代表未降雨时的样本,三角形代表降雨时的样本.当由温度、相对湿度、降雨组成的控制因子进入分叉集时,腐蚀电偶电流在平衡曲面的下叶和上叶之间跳跃.从图8(a)观测到,降雨会促使腐蚀系统中的电偶电流不能沿着原有的轨迹运动,而是突变到新的演变轨迹上.
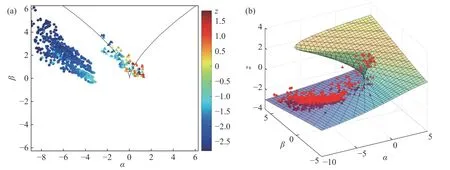
图8 北京大气腐蚀数据在控制平面(a)和平衡曲面(b)上的分布Fig.8 Distribution of the Beijing atmospheric corrosion dataset on the control plane (a) and equilibrium surface (b)
3 结论
(1) 对于存在突变现象的系统,通过理论和数据相结合的方式建立尖点突变模型是一种有效的建模手段.
(2) 提出了基于变量选择的尖点突变模型的两步构建方法.在具有突变特征的数据集上,相比于其他模型,利用本文所提方法构建的尖点突变模型拟合效果更优.
(3) 结合样本在控制平面和平衡曲面的分布图,尖点突变模型可以解释系统的突变行为.
