基于复杂网络的研究生课程群建模和分析

杨志飞，闫光辉，罗 浩，常文文

（兰州交通大学 电子与信息工程学院，兰州 730070）

随着研究生的不断扩招，研究生规模不断扩大，研究生管理数据也日趋庞大，这些数据看似毫无关联.在大数据时代，找到它们之间有效的关联，分析其关联关系，有利于发现其相互作用［1］.同时随着智能产业的兴起，导致了工程系统社会化、社会系统工程化、简单系统复杂化的新趋势，研究生教育也得到了很好地发展［2］.目前，我国的研究生教育已经成为培养高层次人才、支撑自主创新的战略性力量，也是推进创新型国家的构建和“中国梦”实现的主导力量［3］，因而需要优化课程教学管理，不断推动教学改革与创新［4］.研究生教学管理主要为学术型研究生和专业型研究生［5］.课程体系是专业培养的重要内容，是实现人才培养的最主要途径和最重要的基础，是实现人才培养方案的依托.2019年3月，教育部发布教研厅［2019］1号文件《教育部办公厅关于进一步规范和加强研究生培养管理的通知》明确要求，要坚持“服务需求，提高质量”的研究生教育发展主线，优化和完善方案设置.构建多元化的研究生课程体系势在必行［2］，分析课程间的关系有利于构建优质的课程体系，有利于解决研究生学习的多样性问题.复杂网络是根据数学方法、图论等发展起来的定量分析方法，是研究复杂系统的新视角.复杂网络目前已经应用在自然科学与社会科学研究的各个方面，比如疾病传播、气象动力学、历史演化等.在教育方面，复杂网络也有了一定的应用，通过分数将课程关联，分析本科专业核心课程［6］；挖掘课程内知识点，构建网络模型，优化教学过程［7-8］.本文将复杂网络作为研究生课程群体系的建模原理，以研究生培养计划为基础，将其定义为选课关系，对研究生课程进行建模和分析，探索研究生课程间的关联关系，同时借助网络分析可视化工具，直观地展示各专业培养方案中课程之间的结构以及关联关系.最后，以兰州交通大学电子与信息工程学院研究生培养方案中的课程为例，并将课程作为一个向量，通过每门课程中的学生集合建立课程之间的关联，计算其相关关系，将课程间的复杂关系通过网络图的方式呈现；将学生集合作为课程的重要属性之一并融合两种网络结构分析课程重要性.

1 基于选课关系的课程群复杂网络建模和分析

1.1 课程群复杂网络建模

采用复杂网络技术对研究生选课关系的课程群建模，从而可以利用复杂网络中的社团划分、重要节点排序对课程群进行分析，同时将复杂网络技术应用于研究生课程群的建设，其建模过程可以定义为Stu-Course-CN，其建模流程如下：

1）根据研究生培养方案建立每学期的课程群ΩC=｛c1，…，ci，…，cM｝，其中的ci表示第i门课程.

2）根据研究生的培养计划建立每门课的选课学生集合ΩSi=｛fi（ci）｝，其中：ΩS=｛s1，s2，…，sN｝为选课的学生集合；｛fi（ci）｝为第i门课程的学生集合.

3）剔除学生集为空的课程，将非空学生集的课程定义为选课课程群=ΩC＼｛ci|ΩSi=Ø｝；然后，计算选课课程群中课程之间的学生集的交集，Numij=|ΩSi∩ΩSj|为第i，j 2门课程之间的共有学生数.

4）根据复杂网络邻接矩阵原理，建立基于Numij的网络关系，其邻接矩阵为

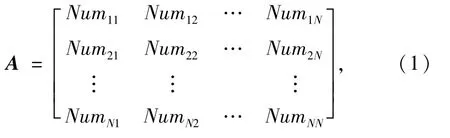
定义该网络为选课课程群网络.

1.2 课程群聚类和社团分析

为了分析选课课程群的内在关系，对课程群网络结构进行社团分析.课程群网络结构的社团研究可以揭示错综复杂的课程群网络如何由相对独立又相互交错的社团构成.根据社团内的节点之间连接非常紧密而社团间的连接却相对稀疏的现象，分析课程群的社团结构，对了解课程群网络结构和分析网络特性具有极为重要的意义，并且可以进一步帮助发现课程之间的聚类关系，为课程群建设、排课安排等提供一定的应用价值.

课程群网络的社团分析算法分为3个阶段，这3个阶段重复迭代，定义为stepA算法［9-10］.假设课程群网络为由N门课程组成的N个节点的加权网络，同时采用网络模块度的度量准则模块度增益ΔQ.定义社团B的模块化增益为

第1阶段，完成初步社团划分，计算步骤如下：

1）为每个节点分配一个社团，此时社团数等于节点数.

2）对每个节点i，考虑其邻居节点j，将节点i从其社团移除，并将其放置在j的社团中.

3）计算每个社团的模块化增益ΔQ.若ΔQ≥0，则保留i在j社团中，完成一次社团节点的移动；若ΔQ＜0，则i恢复到原来的社团中，节点社团移动失败.

4）遍历所有的节点.

5）当模块化增益不再有正值时，第1阶段完成.

第2阶段，完成新网络构建，计算步骤如下：

1）将第1阶段形成的社团视为节点；

3）生成新网络；

4）对新网络采用第1阶段步骤对其进行迭代计算.

第3阶段，判断模块化增益是否为最大值，若不是最大值继续第1阶段和第2阶段，否则结束社团划分.

stepA算法计算示意图如图1所示.首先，通过计算模块度增益及对其的优化过程形成新社团；其次，根据社团划分建立新网络.重复这2个阶段直到模块化增益达到最大值.

图1 选课网络社团分析步骤Fig.1 Analysis steps of course selection network community

1.3 课程节点重要性分析

在选课课程群网络中，有必要对该网络中的课程进行重要性分析，发现和挖掘选课关系下课程的重要性，为下一步的课程建设做支持.在复杂网络中，刻画节点重要程度的一个指标就是节点中心化，用于定量表示网络中一些节点比其他节点更重要或处于更中心的位置，该指标用于确定网络中个体所处位置与其在群体中的影响之间的关系，已广泛应用于保障体系［11］、燃气管网［12］、传输效率［13］和个人绩效［14］等方面.节点重要性的度量方法主要有节点度、特征向量和接近度等，但这些指标仅考虑网络中节点的结构关系.在选课关系网络中，在兼顾课程群网络节点的结构关系的同时引入课程属性（尤其是课程的选课人数），以便对课程重要性进行多属性［15-16］分析.

1）网络结构的局部信息处理.在基于选课关系的课程群网络结构中，虽然度指标能直接反映一个节点对网络中其他节点的直接影响力，但拥有大量连接的邻居节点可能有更大的影响力，也就是在选课课程群网络结构中节点的重要性不仅与自身的信息有关，而且与该节点的邻居节点的度也存在一定关联，即该节点的度及其邻居节点的度越大，节点越重要，可以采用一个多级邻居信息指标以及其邻居之间的紧密程度对网络中的节点重要性进行度量，将其定义为基于邻居信息与集聚系数的节点重要性评价方法（P（i））［17］.

其中：fi为节点vi自身的度与其所有邻居vu度之和，即fi=k（i）+k（u），k（u）表示节点vu的度，Γ（i）表示当前节点vi的邻居节点集合；cci为节点vi的集聚系数；G为整个网络节点集.

2）网络结构的全局信息处理.基于网络全局属性的节点重要性度量主要考虑网络全局信息，特征向量指标不仅考虑全局网络信息，同时考虑了邻居节点的重要性程度.特征向量指标强调节点之间的相互影响，节点的重要性不仅与其连接的边数有关，而且和连接节点的重要性成线性关系，设网络具有N个节点，A表示网络的邻接矩阵，λ1，λ2，…，λN表示A的N个特征值.设λ为矩阵A的最大特征值，有

其中：aij为A中元素；ei为节点i的重要性度量值；ej为节点i邻居节点的重要性度量值.则节点i的特征向量指标可以定义为

3）网络节点选课人数属性处理.根据Stu-Course-CN建模流程，计算每门课的学生人数si，形成课程人数集合s=｛s1，…，si，…，sN｝.人数是选课的最重要的属性，对其归一化处理，归一化公式为

因选课中最大人数不等于最小人数，所以s′i∈（0，1）.

在选课的课程网络中，需要充分考虑网络的局部信息和全局信息，同时融合选课人数信息，为此定义课程重要性指标为

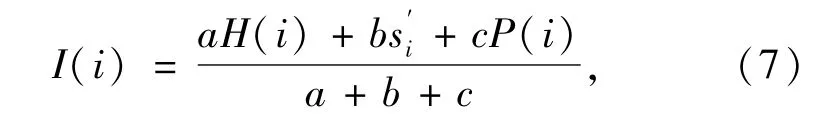
2 仿真实验和结果分析

2.1 数据来源和建模结果

采用兰州交通大学电信学院研究生连续3年的选课情况作为分析对象.本文以2018年第2学期研究生的选课情况为例，实际开课共33门，研究生182名，3个专业方向（信息与通信工程、计算机科学与技术、电子科学工程）.为了便于分析，对课程进行编号处理，定义如下：1代表功率电子学；2代表大规模集成电路CAD；3代表可信计算与信息安全；4代表基于FPGA的数字系统设计；5代表现代半导体物理与器件；6代表应用统计学；7代表机器学习；8代表模糊数学及应用；9代表深度学习；10代表最优化方法及应用；11代表DSP技术及开发；12代表通信网协议分析与管理；13代表通信系统仿真技术；14代表软件无线电技术；15代表数字图像处理；16代表语音信号处理；17代表信号检测与估值；18代表应用密码学；19代表无线通信技术与应用；20代表轨道交通通信技术；21代表无线通信网络规划与优化；22代表软件体系结构；23代表智能计算；24代表数据挖掘；25代表现代数据库技术；26代表网络安全技术；27代表神经网络理论与应用；28代表统计决策与模式识别；29代表分布式系统；30代表高级计算机图形学；31代表智能铁路运输系统（ITS-R）；32代表科技英语写作（信息类）；33代表虚拟现实技术及应用.根据式（1）获得课程之间的邻接矩阵（见表1），采用Stu-Course-CN构建学生培养计划下的课程之间的复杂网络，网络如图2所示，该网络共33个节点，468条边.从图2的选课关系网络中可以发现：该网络为稠密网络，大部分课程之间具有较为稠密的连接，仅个别课程连接比较稀疏.从该网络中无法直接获得课程的专业方向以及课程的重要性，为此需要对该网络进行社团和重要性分析.

图2 选课关系的课程复杂网络Fig.2 Course complex network of course selection relationship

2.2 社团分析

为了挖掘网络结构中隐藏的信息，对该33门课的选课关系课程群网络采用stepA算法进行社团分析，结果如图3所示，最终模块度ΔQ收敛于0.171，社团划分为三类，分别为：电子科学方向，包括1，2，4，5，15，25等6个节点；计算机方向，包括3，6，7，10，18，22，23，24，26，29，32等11个节点；信息与通信方向，包括8，9，11，12，13，14，16，17，19，20，21，27，28，30，31，33等16个节点.与培养方案进行比较，社团划分与培养方案课程划分一致.图4为培养方案的课程关系，在培养方案中，15（数字图像处理）、25（现代数据库技术）和32（科技英语写作（信息类））3门课为3个培养方向的共有课程，但15（数字图像处理）内容偏重信息与通信方向，25（现代数据库技术）内容偏重计算机方向；18（应用密码学）、24（数据挖掘）、26（网络安全技术）、27（神经网络理论与应用）和30（高级计算机图形学）是计算机方向和信息与通信方向的共有课程，但18（应用密码学）内容偏重于信息与通信方向，24（数据挖掘）、26（网络安全技术）、27（神经网络理论与应用）和30（高级计算机图形学）4门课程内容偏重于计算机方向.从图3的选课网络社团划分可以看出：15（数字图像处理）、25（现代数据库技术）在分类中属于电子科学方向，说明这两门课程主要选择的学生为电子科学方向学生，可能同这学期电子科学方向开课的课程数少有一定的关系；30（高级计算机图形学）属于信息与通信方向分类，说明该课程主要由信息与通信方向的学生进行选课.从上述分析中可以得出：基于学生选课关系网络的社团划分和培养方案是一致的，说明该方法在选课网络中是可行的.同时从社团划分中也可以看出个别课程的主要选课学生的学科方向，对后期的培养方案修订具有一定的意义.

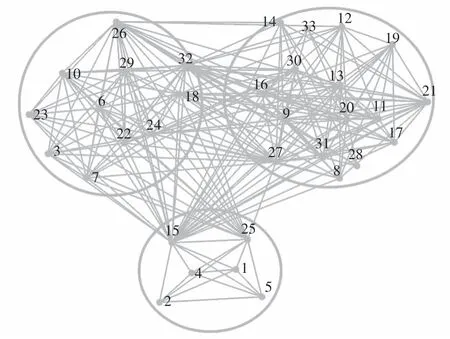
图3 课程群的社团划分Fig.3 Community division of curriculum group

图4 培养方案课程关系Fig.4 Relationship between training program

2.3 选课关系课程群课程重要性分析

为了进一步挖掘课程的有效信息，采用式（7）对选课关系课程群的课程重要性进行分析，其结果如图5所示，图中列出了选课人数属性下的课程重要性分析、网络结构特征的课程重要性分析以及二者融合的重要性分析.从图5中可以看出：绝大多数的课程在这3种分析下重要性具有一致性，但机器学习、数字图像处理、轨道交通通信技术、数据挖掘、现代数据库技术、分布式系统以及科技英语写作（信息类）等7门课程值得注意，从这7门课程可以看出，这7门选课人数都很多，在网络结构影响下其重要性虽没有变化，但对其重要性幅值带来了一定的约束，重要性值更加合理；同时有个别课程二者的重要性不同，如模糊数学与应用，虽然其选课人数少于应用统计学，但其融合后的重要性大于应用统计学，说明网络结构关系提升了其重要性；另外，还有分布式系统、应用密码学和现代数据库技术，这些课程的网络结构直接影响了融合后的重要性分析，使得选课人数多的分布式系统的重要性低于应用密码学和现代数据库技术.从整体上而言，基于选课关系网络课程的重要性能够反应学生的喜好，通过网络关系可以反应选课关系对课程重要性的影响.

图5 课程重要性分析Fig.5 Curriculum importance analysis

3 结论

本文首先对研究生课程群的选课关系进行了分析，建立了选课关系下的课程群复杂网络模型，随后分析了在选课关系下的课程群社团结构，并和培养方案进行了比较，结果表明：该社团结构同培养方案是一致的，同时也挖掘出个别课程主要为某一个学科方向的学生选择，为培养方案的修订提供了一定的依据.接着，采用网络结构指标、选课人数属性以及二则的融合对选课关系下的课程重要性进行了分析，从分析结果可以看出学生选课的兴趣倾向于该门课程在学生中的影响力，这对课程评价有一定的参照价值，同时也有利于研究课程的合理性安排.总之，通过复杂网络对研究生课程进行建模不仅能分析课程在课程体系中的重要性，同时为后续的课程管理与学生兴趣相结合提供依据.