泡沫铜结构及浸润性对液体渗吸特性的影响

张晨阳，贾志海，黄宝罗，康学良

(上海理工大学能源与动力工程学院，上海 200093)

波形板汽-水分离器由于具有分离效率较高、阻力小、破膜速度高等优点，常作为汽-水分离系统最后一级分离器，被广泛应用于核动力装置中。它可将蒸汽干度提高到99%以上，保证了核动力装置的安全运行。

影响波形板汽-水分离器分离效果的结构参数很多，如波形板屈折角、波形板节距、波形板间距、单双钩、挡板等[1-3]。同时入口参数，如流速大小、颗粒直径和蒸汽湿度也会影响波形板汽-水分离器的分离效果[4-5]。因此，目前的研究主要是通过分析结构参数和入口参数来提高波形板汽-水分离器的分离效率，从其材料自身特性进行探讨提高分离效果的研究还鲜有报导。

近年来，随着金属多孔材料的发展，越来越多性能优异的金属多孔材料被应用到相变蓄热[6]、沸腾换热[7]及撞击吸能[8]等领域。在采用的诸多材料中，泡沫铜材料具有孔隙率大、性质稳定、亲水性和渗吸性等特性[9-11]， 尤其适合应用于汽-水分离领域。为此，本文将对多孔泡沫铜材料应用于汽-水分离领域进行探讨，通过分析泡沫铜结构和浸润性对液体渗吸特性的影响，为多孔泡沫铜材料在汽-水分离领域的应用提供参考。

1 实验装置与材料

1.1 实验装置

实验装置如图1所示。首先利用实验台架将SH-2型拉力计固定，通过数据线连接拉力计和计算机，实验中测量数据将在计算机实时显示并记录，拉力计的测量范围为±2 N，负荷分度值0.000 1 N，示值误差±0.5%，采样频率10次/s。拉力计和待测试的泡沫铜片通过挂钩相连，并保持水平状态。将装有去离子水的水槽水平放置于泡沫铜片底下，并通过升降台控制水槽高度。当水槽水面和泡沫铜片下表面即将接触时，提前启动拉力计，记录拉力计的测量数据。通过监测泡沫铜样品接触水面后，拉力计的示数变化，得到渗吸质量和时间的关系。

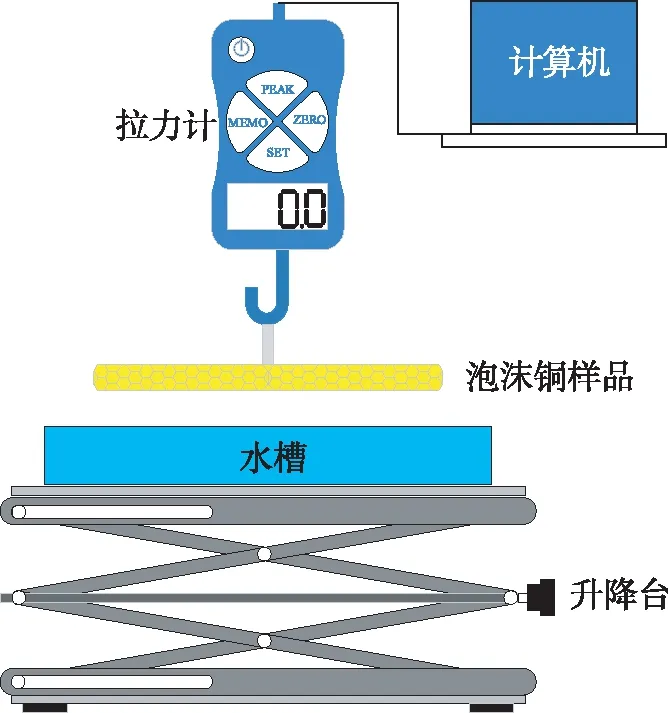
图1 实验装置

1.2 泡沫铜材料

实验采用的泡沫铜材料样品参数如表1所示。样品尺寸规格是厚×宽×长为2 mm×50 mm×50 mm。为了分析孔隙率和孔径对泡沫铜渗吸能力的影响，将泡沫铜样品按照孔隙率和孔径的不同划分为四组。第一组、第二组各自有效半径相近而孔隙率不同，第三组、第四组各自孔隙率相近而有效半径不同，通过控制变量的方式，分别研究孔隙率和有效半径对渗吸能力的影响。图2为采用Dino AM7915相机获取的泡沫铜结构照片，放大倍率为100倍，可以看到，本实验采用的泡沫铜样品是一种由相互贯通的五边形孔洞构成的网络结构。

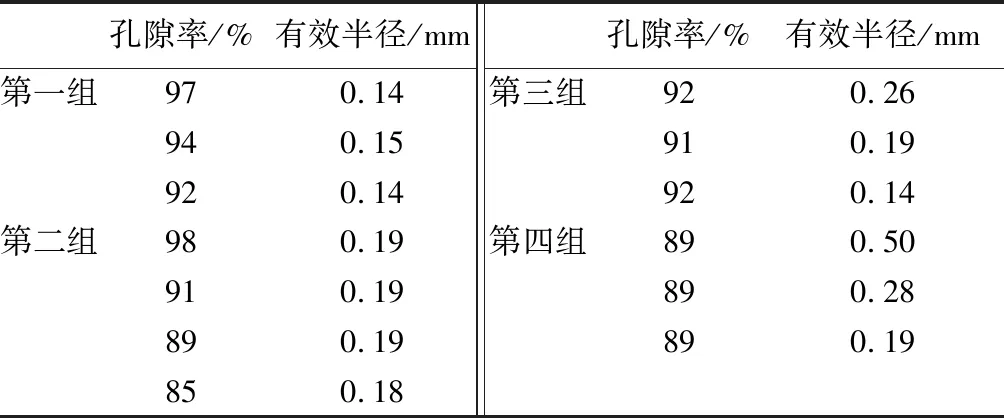
表1 泡沫铜样品结构参数

图2 泡沫铜样品显微结构

2 数学模型

将水从泡沫铜表面渗吸至内部的过程看成由n根等直径均匀分布的毛细通道的自发渗吸过程，假设流动服从Hagen-Poiseuille定律，则圆形直毛细管中的流量q可用Hagen-Poiseuille方程表示：

(1)

式中：μ为流体动力粘度，L0为毛细管长度，Δp为沿毛细管的压降，λ为毛细管直径。

对于泡沫铜多孔介质中的流体流动，流道通常是非圆形和曲折的。WILLIAM[12]分析了这些因素的影响，对曲折通道和非圆形通道层流的Hagen-Poiseuille方程进行了修正，即：

(2)

式中：k为几何校正系数，Dh为水力直径，La是弯曲毛细管的实际长度。

对于圆柱形毛细管，毛细管压力pc由Laplace-Young方程可得：

(3)

式中：σ是气液界面的表面张力，θ为动态接触角，R为孔隙半径。

对于泡沫铜多孔介质不规则的孔隙结构，FRANKEN[13]引入了几何修正系数B获得了不规则形状孔隙的Laplace-Young方程，为：

(4)

式中：r为有效半径，对于圆柱形孔隙，B= 1；对于非圆柱形孔隙，B< 1。

这样，重新简化公式(2)和(4)，可得到适用于具有可变形状孔径的弯曲毛细管的修正Hagen-Poiseuille和Laplace-Young方程，即：

(5)

(6)

式中：α为无量纲几何校正系数，α≥ 1。对于圆形横截面的毛细管，α=1；对于五边形，α=1.088。

当弯曲的非圆形横截面毛细管与湿润液体接触时，液体将在大气压力pa、静水压力ph和毛细管压力pc之间的平衡下浸渍毛细管，总压降为：

Δp=pa+ph+pc

(7)

如果毛细管有两个开口端，则pa= 0。对于薄层泡沫铜的渗吸过程，高度变化为2 mm，将静水压力近似为零，ph= 0。因此得到：

(8)

将公式(8)代入公式(5)得到弯曲毛细管的浸渍速度：

(9)

式中：υa(t)是t时刻弯曲毛细管中的浸渍速度，La(t)是t时刻弯曲毛细管中浸渍的实际长度。

为了描述泡沫铜多孔介质中流线的迂曲度，通常采用参数迂曲度τs，定义为：

(10)

因此迂曲速度和直线速度可分别表示为υa=dLa/dt和υ0=dL0/dt，因此υa和υ0的关系为：

υa=τsυ0

(11)

将公式(11)代入公式(9)可得：

(12)

渗吸到泡沫铜中的液体的累积质量为：

M(t)=ρAφL0(t)

(13)

式中：ρ是去离子水的密度，A是泡沫铜的横截面积，φ是泡沫铜的孔隙率，L0(t)是t时刻液体吸收的平均高度，将公式(13)对时间t求导，有：

(14)

将公式(12)代入公式(14)，得：

(15)

对公式(14)积分，可得[15]：

(16)

在低毛细数下(Ca< 2×10-6)，动态接触角θ近似等于静态接触角θe[15]，由于实验中各泡沫铜样品在渗吸过程中的毛细数均小于2×10-6，因此可通过测量泡沫铜样品的静态接触角来确定渗吸过程中的动态接触角的值。

将泡沫铜样品竖直地接触水面，接触面积为A，测量吸收到泡沫铜中液体的最大重量，此时毛细力与重力平衡，满足：

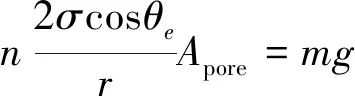
(17)

式中：n为孔隙数量，n=A/Apore；θe为静态接触角；Apore为单个孔隙的面积；m为泡沫铜最大渗吸质量；g为重力加速度。

化简和整理公式(17)，可得：

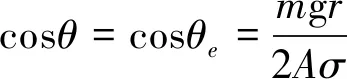
(18)

迂曲度τs由式(19)确定[16]：

(19)

式中：ξ是颗粒的形状因子，本文中ξ取0.153[16]。

3 结果与讨论

3.1 孔隙率的影响

第一组、第二组各自有效半径相近而孔隙率不同，由于迂曲度τs只与孔隙率有关，因此将第一组和第二组表面的孔隙率参数代入式(19)可获得各样品的迂曲度。

同时对实验采用的第一组和第二组泡沫铜样品进行分析可知，同一组别内有效半径变化不大，影响渗吸能力的主要因素为孔隙率。在同一组别的泡沫铜样品中，对渗吸能力最好的泡沫铜样品进行静态接触角分析，同一组别的泡沫铜样品取同一静态接触角。最终通过实验得到第一组和第二组的静态接触角分别为15.8°和49.7°。静态接触角不同，导致表面张力在竖直上的分力不同，渗吸的驱动力拉普拉斯力也不一样，从而影响泡沫铜的渗吸性能，在相同的条件下，静态接触角越小，渗吸能力越强。

将相关参数代入式(16)可得理论的渗吸质量和时间的关系，如图3和图4所示。

图3所示为300 s内第二组泡沫铜样品的渗吸实验和理论值的对比，发现随着孔隙率的增加，泡沫铜样品的渗吸能力先增加后降低，孔隙率91%时的渗吸能力最强，当孔隙率为98%时，渗吸速度最慢，导致理论曲线和实际值有很大的偏差。

图4所示为第一组实验数据，随着孔隙率的增加，泡沫铜样品的渗吸能力一直降低，孔隙率92%时的渗吸能力最好。同时也可以看到随着孔隙率的变大，理论曲线和实际值的误差越来越大。根据理论分析可知，随着孔隙率的增加，迂曲度逐渐减小，相同有效半径的泡沫铜样品，此时的渗吸能力应逐渐增强。但由于孔隙率的增加，孔隙分布变得分散，此时单个孔的渗吸能力不变但孔与孔之间的间距加大，液体流经一个孔后可顺利流经下一个孔的几率变小，导致液体无法顺利通过孔隙，此时泡沫铜样品的内部可看成由n根一端封闭的毛细通道组成，因此渗吸能力减小，并且这种现象随着孔隙率的增加变得更加显著。孔隙率对泡沫铜渗吸能力具有双重影响，且存在一最佳孔隙率，此时具有最优的渗吸能力。

图3 第二组表面渗吸质量和时间的关系

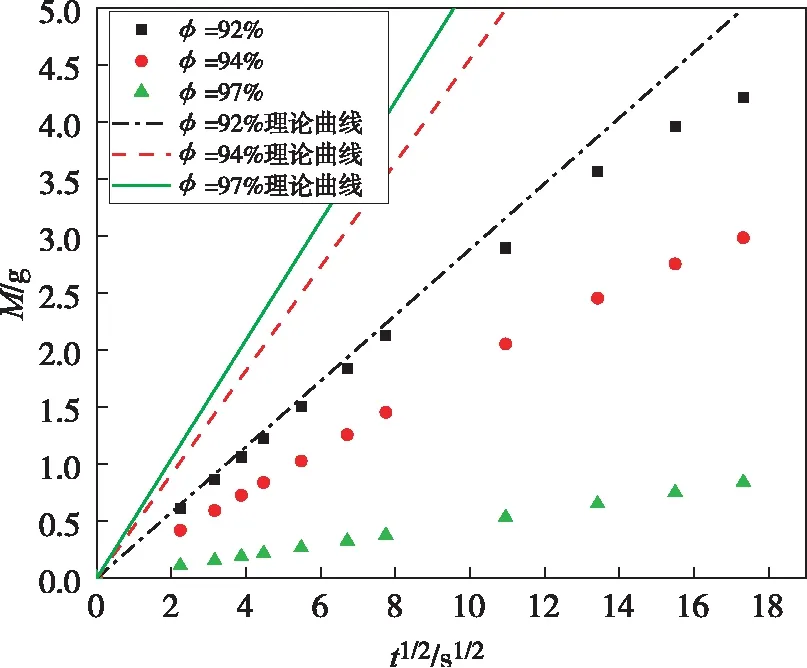
图4 第一组表面渗吸质量和时间的关系

分析图3和图4可知，对于渗吸能力强的样品，如φ=91%、φ=92%，随着渗吸的进行，越到后期实验值和理论曲线的偏差越大，这是由于在实际情况中泡沫铜内部的渗吸过程并不是均匀的，同时液体并不会完全浸润每一个孔隙，存在局部润湿不均的情况，最终导致实验值小于理论值。

将第一组、第二组不同孔隙率下渗吸速率的实验值和理论值进行对比，如图5所示，获得不同孔隙率下渗吸速率实际和理论的比值散点图，并进行曲线拟合，得到了关于孔隙率的修正函数R，使不同孔隙率下渗吸速率的实验值和理论值相符，即：

(20)

图5 不同孔隙率下理论和实际偏差值

对比实验数据和理论公式，发现当孔隙率高于91%时，理论公式和实际误差较大，此时对公式(16)进行修正，引入关于孔隙率的修正函数R，获得适用于高孔隙率下的理论公式：

(21)

对修正后的理论公式(21)进行分析，分离并提取关于孔隙率φ的变量，单独分析孔隙率的变化对渗吸能力的影响，获得函数f(φ)。

(22)

图6所示为函数f(φ)随孔隙率的变化曲线，随着孔隙率的增加，函数f(φ)的值先缓慢增大后快速减小，最后稳定在0.05左右。在孔隙率91%～93%之间存在一个峰值，此时函数f(φ)的值最大，最大值为0.425。因此对于不同孔径的高孔隙率的泡沫铜，都存在一个最佳孔隙率，范围为91%～93%，此时泡沫铜的渗吸能力最强，和实际情况相符。

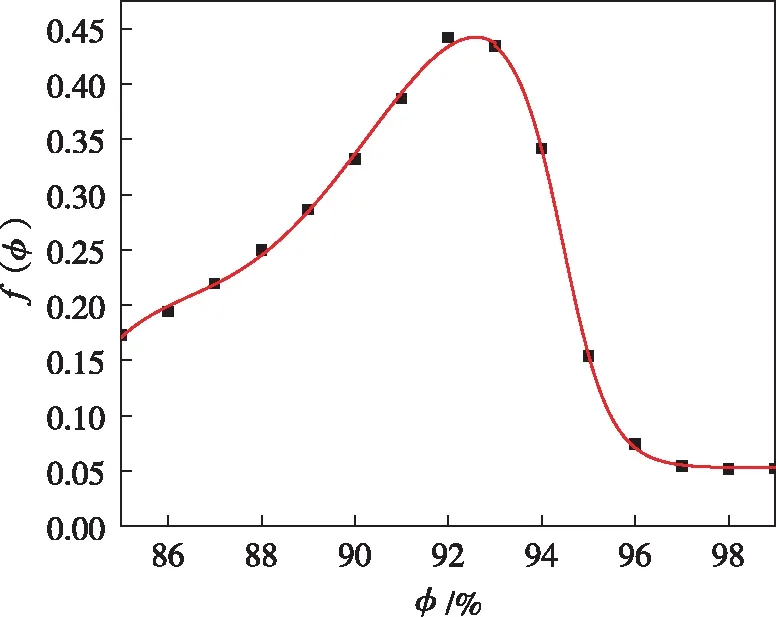
图6 不同孔隙率下孔隙率函数的值

3.2 有效半径的影响

图7、图8给出了第三、四组样品的渗吸质量和时间的关系，此时第三、四组样品各自孔隙率相近而有效半径不同。

图7 第三组表面渗吸质量和时间的关系

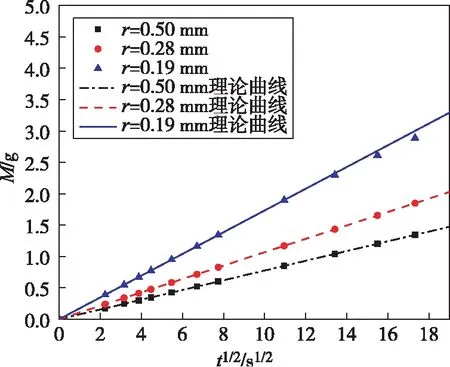
图8 第四组表面渗吸质量和时间的关系

第三组的孔隙率在91%～92%之间，组内泡沫铜样品迂曲度近似，修正后的理论公式和实验结果符合较好。有效半径为0.26 mm、0.19 mm和0.14 mm泡沫铜样品的接触角分别为78.8°、49.6°和15.9°，随着有效半径的减小，相同时间内泡沫铜样品渗吸的液体更多，如图7所示。

第四组的孔隙率为89%，组内泡沫铜样品迂曲度近似，有效半径为0.50 mm、0.28 mm和0.19 mm泡沫铜样品的接触角分别为87.1°、79.9°和47.6°，实验和分析发现随着有效半径的减小，相同时间内泡沫铜样品的渗吸的液体更多，如图8所示。

对不同样品有效半径r和接触角θ的余弦值进行分析，在不同的有效半径r下，cosθ的值是不同的，有效半径r与rcosθ的关系如图9所示。随着r的减小，rcosθ的值逐渐增大，说明在本文泡沫铜样品的有效半径范围之内，减小有效半径有利于泡沫铜的渗吸。对数据进行曲线拟合，发现有效半径越小，曲线斜率的绝对值越大，因此对泡沫铜样品渗吸能力的提升越显著。同时从单个小孔来看，有效半径越小，单个孔的毛细力越大，越有利于表面的渗吸。

图9 不同有效半径下rcosθ值

3.3 浸润性的影响

依次使用稀HCl试剂、亲水试剂和GLACO疏水试剂对r=0.19 mm，φ=91%的表面进行浸润改性，测试原表面、稀HCl清洗表面、亲水表面和疏水表面的渗吸特性，在这四种情况下，对应的泡沫铜样品的接触角分别为49.7°、84.1°、0°和90°，由理论分析可知，在其他参数不变的情况下，浸润性是影响泡沫铜渗吸能力的重要因素。

如图10所示，稀HCl处理后的表面渗吸能力相比于原表面大幅减弱，因为用稀HCl处理原表面时，稀HCl和泡沫铜表面的氧化层发生反应，生成溶于水的CuCl2溶液，将基底的铜暴露出来，和液体直接接触，导致其亲水性变差，使接触角增大，从而降低了表面的渗吸能力，因此泡沫铜样品表面的氧化有利于渗吸能力的增强。

图10 不同浸润性下渗吸质量和时间的关系

同时发现，在GLACO疏水改性下，泡沫铜样品几乎不发生渗吸，此时样品的接触角大于90°，cosθ为负值，根据理论模型，则渗吸质量为负值，与实际情况不符，因此取接触角为90°，cosθ为0，此时渗吸质量为0。

对泡沫铜样品亲水改性后，此时样品的接触角接近0°，可从理论上达到该表面的最佳渗吸性能，亲水改性有利于泡沫铜的渗吸。因此，从浸润性角度而言，材料的亲水性越好，其渗吸能力越强。

4 结语

本文以去离子水为实验工质，研究了泡沫铜结构和浸润性对渗吸能力的影响，结论如下：

(1)孔隙率的增加对泡沫铜样品渗吸能力的影响是两方面的，一方面可以降低迂曲度，对渗吸起促进作用；但另一方面会减小液体流经下一个孔的几率，起抑制作用。随着泡沫铜孔隙率的增加，渗吸能力先增强后减弱。通过对孔隙率的单独分析，得到泡沫铜最佳渗吸时的孔隙率范围为91%～93%。

(2)孔隙有效半径的大小对泡沫铜渗吸能力的影响非常显著，随着有效半径的变化，泡沫铜的动态接触角也会发生变化。在本文有效孔径范围内，其值越小，越有利于泡沫铜的渗吸。

(3)泡沫铜样品在亲水处理后，从理论上可达到该表面的最佳渗吸性能。从浸润性角度而言，亲水性越好，泡沫铜渗吸能力越强。

(4)考虑了孔隙率对泡沫铜样品渗吸能力的双重影响，建立了适用于高孔隙率泡沫铜渗吸能力的理论模型，将模型所得理论值与实验结果进行比较，两者基本一致。