智能助行器防跌倒柔顺控制研究

张钰文，王亚刚，丁大民，林衍照

(1.上海理工大学 光电信息与计算机工程学院，上海 200093； 2.上海康复器械工程技术研究中心，上海 200093)

随着我国老龄化日益严重，因病致残的人口数也逐步上升，对于这些行动不便人士需要使用下肢康复辅助器械提供日常护理和康复训练[1-3]。助行器作为此类器械之一，其主要功能是为用户提供行走时辅助支撑的作用。由于人机紧密接触，所以其安全性对于用户而言十分重要[4]。智能助行器的安全性涉及范围甚广，包括机械结构设计、设备材料选型以及机器与人的交互控制。由于智能助行器是主动引导用户行走，所以应更加重视其使用过程中的安全问题[5-7]。当用户行走过程中有向前跌倒趋势时，目前大多数助行器采用的控制策略都是紧急制动，该操作会给一些存在严重下肢行动问题的用户带来安全隐患，因此有必要对在此类情况下助行器的运动控制做柔顺性的优化，提高设备使用过程中的可靠性。

目前，有部分专家学者对机器人运动过程中防跌倒柔顺控制领域进行了研究。文献[8]提出一种基于手杖机器人的防跌倒控制， 但其缺点是手杖容易侧翻，未充分考虑安全性。文献[9]提出了阻抗控制和滑模控制两种算法结合的动态曲面和针对人在跌倒时的助行机器人运动控制律，但该研究未考虑滑模控制的抖振缺陷。文献[10]提出了一种通过模糊增益来调节的滑模阻抗控制，将感知到的用户意图通过控制算法，减轻了滑模控制的抖振缺陷，达到了下肢康复机器人在主动模式下柔顺性的实现。文献[11]将人运动时所采集的关节数据和运动机理相结合进行研究，引入了滑模控制，并提出基于液压控制的下肢外骨骼机器人思想，这对患者佩戴该设备时的舒适度和安全性都有较大幅度的提升。文献[12]按照人腿部的位置来调节导纳控制器的参数，给跌倒中的用户提供相反方向的支撑力，从而达到防护安全的效果。文献[13]对于助行器在复杂环境中的使用进行了实验，运用了柔顺控制器与导航传感器相结合的一种共享控制器。该研究中，机器人通过不断感知用户的施加力并做出相应响应，使机器能够被动地跟随使用者，但该导航设备较为昂贵。以上研究提出的控制策略多被运用于关节型下肢机器人模型的运动安全性控制，其中使用到的检测防护传感器也过于昂贵。

本文助行器机械结构符合人体力学设计，用户在使用移动过程平稳且不易翻到。此外，本文通过结合低成本阵列式薄膜压力传感器和超声波传感器实现了一种新型的主动柔顺性控制。柔顺控制存在两类特性：主动柔顺性和被动柔顺性[14]。主动柔顺性就是让机器通过力反馈，根据控制策略主动控制其运动。其控制思路为：首先简化助行器建立简化动力学模型；然后选择便于使用力误差作为输入信号的阻抗控制，并结合具有鲁棒性较强的滑模控制对位置进行控制跟随，提高在不确定环境下系统的稳定性；最后，引入自适应的控制概念，以便在滑模控制器参数不确定的情况下达到理想控制效果，并消除不连续开关特性引发的系统抖振问题。本文实验结果证明若用户发生跌倒，采用基于该控制策略的助行器能在平地和坡道上实现安全驻停。

1 控制模型建立

1.1 助行器动力学系统模型

当用户在使用助行器过程中有向前跌倒的趋势时，位于助行器两端扶手的压力传感器与安装在腿部位置处的激光传感器可通过数据融合算法识别出用户意图，检测出是否有跌倒趋势，从而使设备执行防跌倒安全策略。压力传感器采用的是阵列式薄膜压力传感器，能够实时将人机交互力转化为电压信号值，再经过变量转换、信号放大等操作将其作为控制电机驱动的信号值，进而达到同时进行检测与控制的运动控制效果。助行器样机如图1所示。

图1 助行器样机图Figure 1. Model machine diagram of the walking-aid

由于控制策略主要通过力与位置作为控制信号进行转换，故从动力学理论出发将人与助行器作为整体来设计被控对象的模型。为了方便对其进行分析，本文绘制了用户向前跌倒时的人机状态简化图，如图2所示。

图2 用户向前跌倒时的人机状态图Figure 2. Human-machine state diagram of a user falling forward

根据图2所示的简化模型图，将助行器作为受力分析对象并结合牛顿第二定律，得出以下计算式

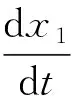
(1)

(2)

式中，x1为人双脚之间的点到助行器前轮的距离；x2为助行器的运动速度；m为助行器质量；r为助行器前轮半径；F为人跌倒时对助行器的作用力；u(t)为助行器驱动电机的控制量。

1.2 助行器阻抗控制模型

阻抗控制通过分析物体末端的运动状态和其受到外力之间的动态关系[15-16]来建立力-位置控制。本文设计将助行器的压力采集器置于两扶手末端，通过阻抗控制分析可以得到助行器末端的位移、速度和加速度。弹簧阻尼质量模型是关于弹簧结构末端受力与其位移、速度和加速度的函数，故可以相互等效。在用户使用助行设备时，人手与扶手端触碰产生作用力，而不是直接与周围环境接触，因此构建模型图时还需考虑扶手端与人体接触的瞬间状态。改进后的人-机模拟阻抗模型如图3所示。

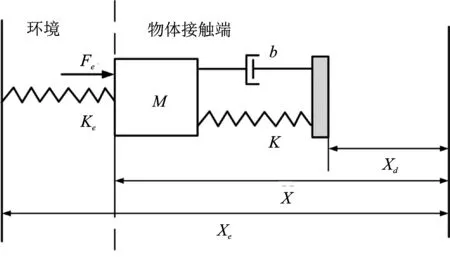
图3人-机模拟阻抗模型图Figure 3. Human-machine simulation impedance model diagram

根据胡克定律，设x为物体实际位置，xd为物体末端相对期望位置，M为物体质量，k为刚度系数，即物体产生单位变形所需的负载，b为阻尼系数，得出物体末端与环境的接触力Fe随物体末端与期望轨迹差的关系计算式，如式(3)所示。

Fe=-k(x-xd)

(3)

如图3所示，可以从扶手末端力守恒的角度列出一种由弹簧、质量和阻尼组成的二阶微分方程。对于物体末端，系统用运动来补偿环境作用力。由于解耦性在阻抗模型中各个环境和方向都适用，仅此可以只考虑某一维度的受力情况，简化后的计算式为

(4)

式中，Md、Bd和Kd分别为质量系数、阻尼系数和环境刚度系数；xn为物体末端实际位置；xd为物体末端相对的期望位置；Fe为物体末端与环境的接触力。

位置阻抗控制主要是通过调节其系统的阻抗系数来实现的。使用力反馈代替力信号的直接控制可以间接反应助行器与其相对环境接触时的动态情况，这样可以选择较为符合的阻抗值。对此，本文分别引入ex(t)和ef(t)来表示位置误差和力误差，并设fx(t)为用户对助行器的期望作用力。通过阵列式压力传感器测量平稳行走时的人机交互力可以得出，在不同场景下的期望作用力不同。fe(t)为用户对助行器的实际交互力，t为时间

(5)

将式(5)带入式(4)中，ef(t)将力误差作为助行器阻抗模型的驱动力，进而得到改进后的助行器阻抗模型，如式(6)所示。

(6)

由于用户向前跌倒时手对助行器两端握把的作用力是逐次递减的，从上式中可以得出，当期望作用力fx趋于0时，人机作用力fe也趋于0，ex位置误差最终为0，能够控制助行器停止在某一期望位置，实现位置跟踪效果。但是在实际人机交互的环境中，还存在物体与环境接触的位置误差，导致被控对象位移无法与期望位移完全吻合一致。如图3所示，还需将环境刚度与环境位置的模型考虑在内，选取xe为环境位置，环境影响值为固定值，ke为环境刚度系数，得到如式(7)所示的环境模型。

fe=ke(x-xe)

(7)

2 自适应滑模-阻抗控制器设计

2.1 自适应滑模控制

通常下肢不便的患者在使用助行器时身体与设备会发生一定的不可控碰撞，从而影响到助行器的正常运动，尤其是在控制助行器柔顺移动的过程中，微小的碰撞也会带来不同程度的干扰。滑模控制是一种对被控对象不连续控制的非线性控制，能够有效抑制外界各种干扰并具有良好的动态响应速度[17-18]，其控制模型是随着系统动态变化的，最终不断逼近期望的状态轨迹[19-20]。

滑模面s的定义与系统参数及扰动无关，设其切换函数为

(8)

式中，ex为位置误差；xd为物体末端相对期望位置；xn为物体末端实际位置；控制参数c>0。再对式(8)求导可得式(9)。

(9)

为了满足在一定时间内形成滑动模态区与系统运动到切换面s=0时的状态需求，同时为了改善助行器在各种不确定环境因素下运行时的扰动影响，本文加入了自适应控制，以期对模型的控制参数做实时补偿调整。本文设计的自适应鲁棒控制率为

(10)

结合滑模控制器，取自适应律为

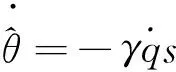
(11)

(12)

对上述滑模控制器稳定性进行分析，定义Lyapunov函数为

(13)

(14)

将式(11)和式(12)代入式(13)，并引进环境的不确性和扰动的未知项Δ，可得

(15)

2.2 自适应滑模-阻抗控制

自适应滑模阻抗控制是一个双环的控制策略，内环为用于实现位置控制的自适应滑模控制器，外环为力反馈控制的阻抗控制，其控制框图如图4所示。

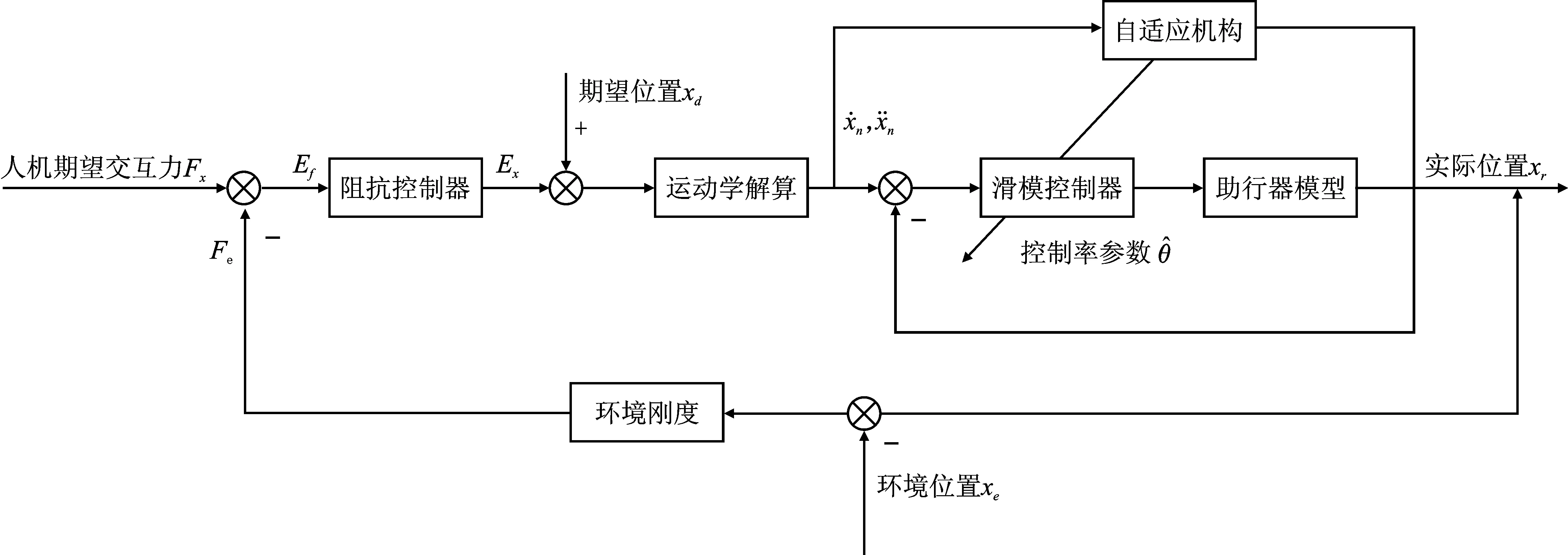
图4 助行器防跌倒柔顺控制框图Figure 4. Compliant control block diagram of the walking-aid against falling

3 仿真分析与实验

为了检验控制策略可行性，使用Simulink对上述控制器进行仿真实验。智能助行器控制系统主要参数如下：质量m=30 kg，取阻抗控制器中惯性参数Md=0.03，阻尼参数Bd=1 500，刚度参数Kd=0.05。滑模控制器中参数通过不断调整，多次仿真实验得出最佳结果为：控制参数c=3，可调增益ks=10，鲁棒性参数η=600。自适应控制器中估计参数最大值θmax=1.5和最小值θmin=0.5，调节参数γ=2。考虑到环境的不确性和扰动，设环境刚度系数Ke=5 N·m-1，环境位置xe=0.05 m。期望助行器与人停止的相对位移xd=0.57。

仿真实验1当用户使用助行设备发生向前跌倒趋势时，助行器完成人体姿态校正后，用户停止继续前进，即人与助行器作用力由大到小逐步衰减。经过压力传感器测量，此情况下人使用助行器时力为20 N左右，对此，假设输入人机交互力参考值为Fx=20e-tN，在t=0～8 s时得到如图5～图7所示结果。

图5 仿真实验1中实际人机作用力图Figure 5. Diagram of actual human-machine force in simulation experiment 1

图6 仿真实验1中人机位置误差图Figure 6. Diagram of human-machine position error in simulation experiment 1

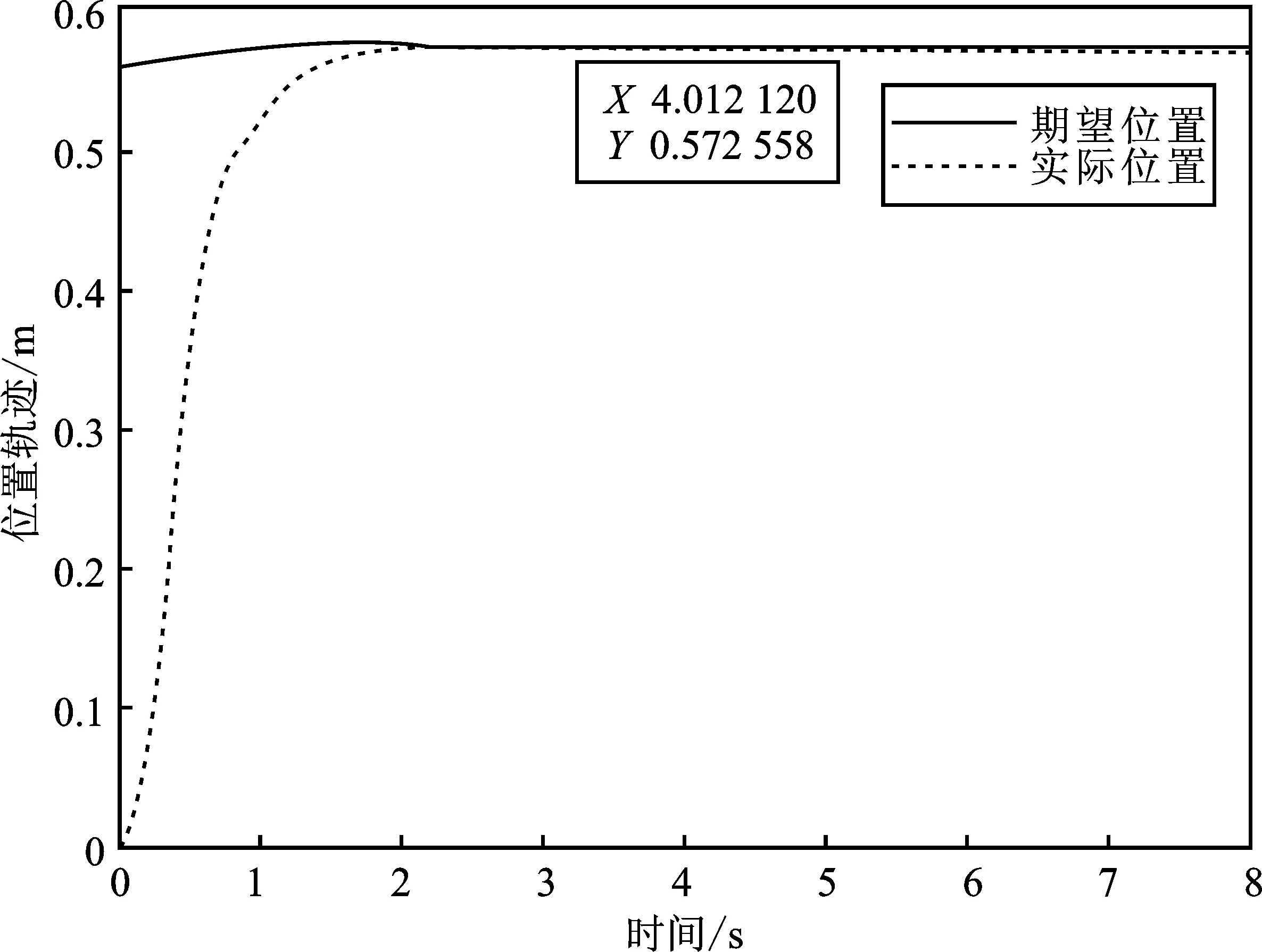
图7 仿真实验1中助行器位置轨迹图Figure 7. The position and trajectory of the walking-aid in simulation experiment 1

仿真实验2当用户使用助行设备发生向前跌倒趋势时，助行器完成人体姿态校正后，用户想要继续前进。经过压力传感器测量，在此情况下人使用助行器时力为25 N左右，对此，假设输入人机交互力参考值为Fx=(20e-t+5) N，在t=0～8 s时得到如图8～图10所示结果。

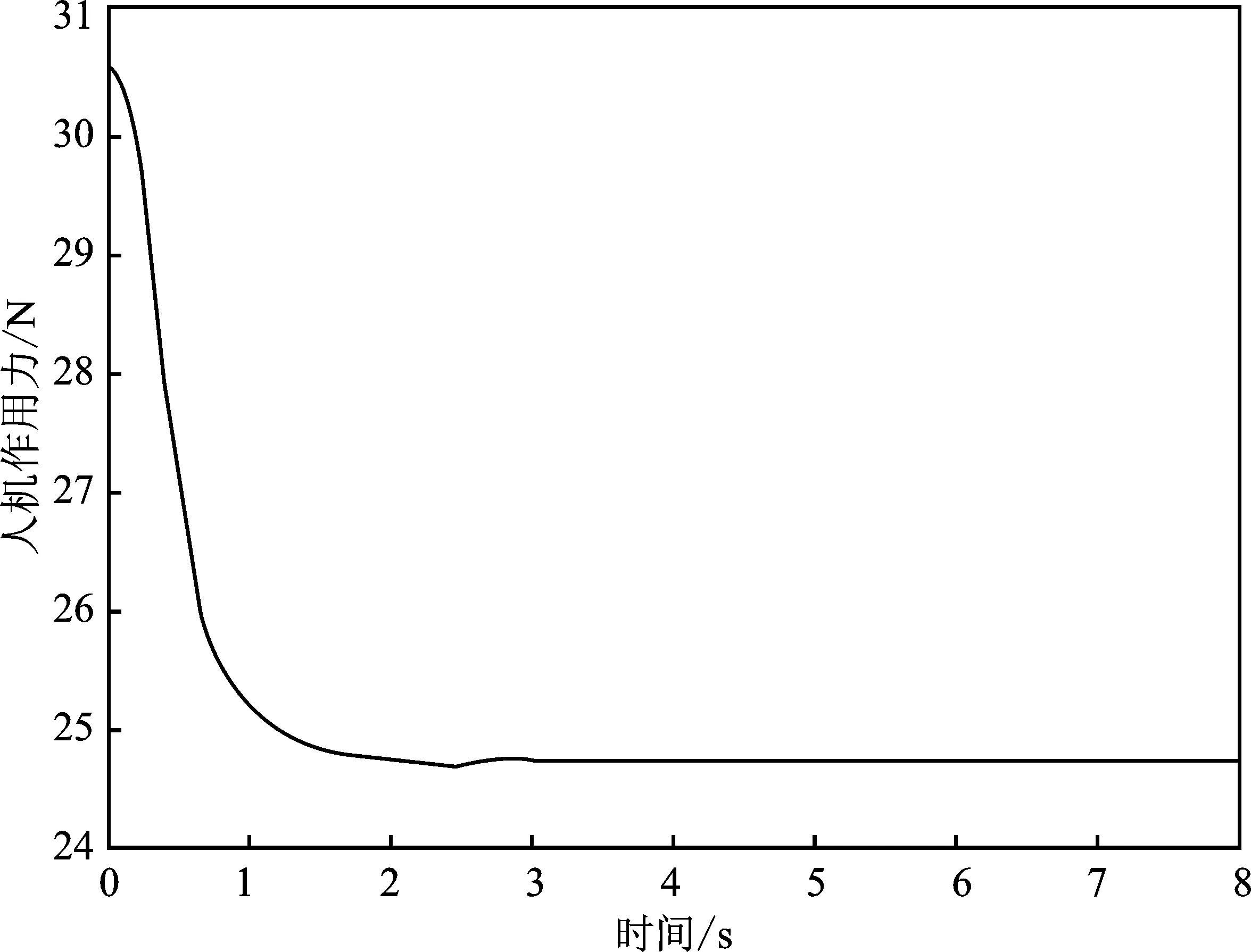
图8 仿真实验2中实际人机作用力图Figure 8. Diagram of actual human-machine force in simulation experiment 2

图9 仿真实验2中人机位置误差图Figure 9. Man-machine position error diagram in simulation experiment 2

图10 仿真实验2中助行器位置轨迹图Figure 10. The position and trajectory of the walking-aid in simulation experiment 2

由仿真实验1可知，在时间约为4 s时，通过压力传感器读取的实际人机作用力为恒定值20 N左右，说明助行器稳定在某一位置，人机相互作用力保持不变。此时，助行器的实际位置与期望位置误差也为0，助行器位置轨迹与期望轨迹重合且一直稳定在期望位置0.57 m左右，并且实际位置稳定后无抖动。该结果证明用户跌倒后想要停止继续前进，助行器完成人体姿态校正并成功停止。

根据仿真实验2的结果可知，3.8 s左右时，通过压力传感器读取的实际人机作用力为恒定值24.8 N，大于仿真实验1中的值，这是因为人与助行器在移动状态下的作用力比静止状态下大。此时，助行器的实际位置与期望位置误差也为0，助行器位置轨迹与期望轨迹重合并一直稳定在期望位置0.57 m左右，并且实际位置稳定后无抖动。该结果证明用户跌倒后继续前进，助行器完成人体姿态校正并继续辅助人前进。

为了进一步验证控制策略的可行性，分别在平地和坡道上模拟用户跌倒后助行器帮助其恢复正立姿势的场景实验，如图11和图12所示。

图11 防跌倒柔顺控制平地实验图Figure 11. Compliant control experiment of the walking-aid against falling on flat groud

图12 防跌倒柔顺控制坡道实验图Figure 12. Compliant control experiment of the walking-aid against falling on slope

实验结果显示，发生跌倒情况时，助行器在平地上可以停止，在坡道上也能平稳驻坡。由于人机作用力与薄膜压力传感器呈线性关系，所以压力传感器读取的电压信号图即为人机作用力变化图。本文采集了助行器速度变化曲线图，如图13所示。由图可知在使用者发生跌倒时，压力传感器电压信号值在4 s之后基本恒定不变，助行器的速度趋于稳定且数值较小，说明助行器已帮助人体恢复正常姿态。

(a)

4 结束语

本文针对助行器使用过程中防跌倒安全性提出了一种基于自适应滑模阻抗控制的柔顺控制方法，来控制助行器运动的轨迹，以便提升用户使用时的安全性。本文依照动力学方程构建助行器被控对象模型，采用滑模控制与阻抗控制的双环控制，构成基于位置的阻抗控制。对于滑模控制器，本文引入了自适应控制律，以防止稳定状态抖振，使得系统的稳定性得到保障。在两种不同实验情况及地形条件下的仿真实验表明，本文提出的控制策略具有较快的跟踪效果，人机作用力与位置误差都在短时间内趋于稳定，说明本文设计可为实现助行器防跌倒运动控制柔顺性提供一定的参考。