以磁通等效实现磁悬浮轴承磁极容错控制
2023-01-04朱芳甫陈亮亮蒋科坚
朱芳甫,陈亮亮,蒋科坚
(1.浙江理工大学 信息学院,浙江 杭州 310018; 2.南昌航空大学 信息工程学院,江西 南昌 330063)
20世纪90年代,作为轴承高端技术,磁悬浮轴承研究逐步兴起。与传统轴承相比,磁悬浮轴承具有无摩擦、无需润滑、转速高、损耗小、转子振动主动控制等技术优势,受到越来越多的关注,逐渐在工业应用中崭露头角。目前,磁悬浮轴承在飞轮储能、大型空压机、分子泵、航天器定位陀螺等领域有较多成功应用的实例,具有良好的推广潜力。本文的关注点在于提升电磁轴承磁极驱动的可靠性问题。传统8极定子结构的电磁轴承运行时需要驱动8路磁极控制回路同时工作,只要其中任一路磁极回路故障,转子悬浮将会失控。针对电磁轴承的磁极驱动可靠性问题,文献[1]提出了一种新的电磁作动器故障诊断算法。该研究通过理论分析负载电流在调制过程中的变化特性,将负载电流的等效斜率定义为故障诊断阈值。文献[2]提出了一种具有较强容错能力的9极径向混合磁悬浮轴承,以提高混合磁悬浮轴承的可靠性。文献[3]在基本拓扑的基础上,提出了两种新型磁力轴承驱动拓扑修正方法,并能保持磁悬浮。文献[4]通过对磁路的分析和力不变性原理的分析,解决了控制电流与一路或相应功率放大器系统故障的关系,得到了故障情况下电流补偿模式。文献[5]针对五自由度磁悬浮轴承系统,提出了一种带容错支路的五相六桥臂开关功率放大器,增加了一个容错桥臂来实现容错操作。文献[6]提出了一种传感器容错控制方法,利用专门设计的小波滤波器对传感器故障进行检测,并在故障发生后利用自检测技术保持系统的稳定性。文献[7]提出一种有串联绕组拓扑结构的容错变流器,在保证DC电压利用率的同时,降低了相脚的电流应力,并实现容错控制。文献[8]提出了种容错重构策略,并验证了两周重构方法的可行性。文献[9]采用提出的电流控制技术避免了在一个机器扇区的开路绕组的情况下出现径向力,并改进了径向力容错控制,以补偿轴承故障或在这种开路绕组条件下的另一个径向力源。文献[10]提出了一种五级嵌套核电厂变流器的故障诊断和容错解决方案。该研究针对故障诊断,提出了一种融合小波包变换和长短期记忆的深度学习方法,并通过仿真和实验验证了容错策略的有效性。文献[11]利用同步镇定理论设计了一种被动容错控制器。文献[12]对一类存在驱动故障的高阶非线性多输入多输出系统,提出了一种具有用于PI增益自动调谐分析算法的低成本容错控制方法。该方法可控制动作连续且能够确保闭环系统所有信号的一致最终有界性。文献[13]以最小功耗分配策略,采用拉格朗日乘子法计算电流分布矩阵,实现了绕组的容错控制。文献[14]提出一种应用于磁悬浮轴承的在线电磁线圈故障诊断方法。文献[15]通过建立数字开关功放输出电流的数学模型,从理论上分析线圈发生故障对输出电流变化率的影响。文献[16]对异步电机进行了电磁仿真采用场路结合的方法将定转子端部的电阻和漏感参数化等效处理到模型中。文献[17]分析了3种不同的电磁轴承结构模型仿真磁场。该研究通过计算,得出了最大承载力的条件和数学表达式,给出了参数设计和计算过程。文献[18]提出采用应急轴承作为辅助支撑,防止电磁轴承停电或掉电时与转自碰撞而损坏。
以往的研究提出了以“电磁力等效”为目标实现容错的方法。当某个磁极回路故障时,由其余正常磁极替代承担故障磁极的电磁力任务,以实现故障前后8个磁极的电磁合力不变,从而实现容错控制。但是,由于电磁力和驱动电流的强非线性关系,难以得出驱动电流和电磁力之间的准确换算关系。此外,电磁力等效的思路方法很难有效处理磁极间由于磁路耦合形成的电磁力耦合。因此,本文提出以磁极端面有效磁通不变的原则实现电磁轴承的容错控制。当某个磁极回路发生故障时,利用其他正常磁极产生耦合磁通,使8个磁极端面的磁通在故障前后保持不变,即“磁通等效”。磁通环境相同,电磁力也自然相同,即可实现容错运行。磁通与电流成线性关系,更利于提高控制精度。
1 电磁轴承的电磁力
8磁极结构是最为常用的径向电磁轴承定子结构,其常采用差动驱动方式,结构如图1所示。两个相邻定子磁极绕组两两串联构成4个C型磁极,而这4个C型磁极可以提供定子径向平面内X、Y轴正反4个坐标方向的电磁力,从而控制转子悬浮。由于在差动驱动方式中,4个C型磁极的电磁力在方向上没有冗余,因此当某个磁极驱动回路发生故障时,不能利用其他磁极实现容错。

图1 8磁极C型磁极差动驱动结构Figure 1. 8-pole C-type magnetic pole differential drive structure
为了能实现磁极回路故障的容错,将4个C型磁极拆分为8个独立的磁极,得到如图2所示的径向8磁极独立驱动的定子结构。该结构在方向上存在冗余,可以实现容错控制。
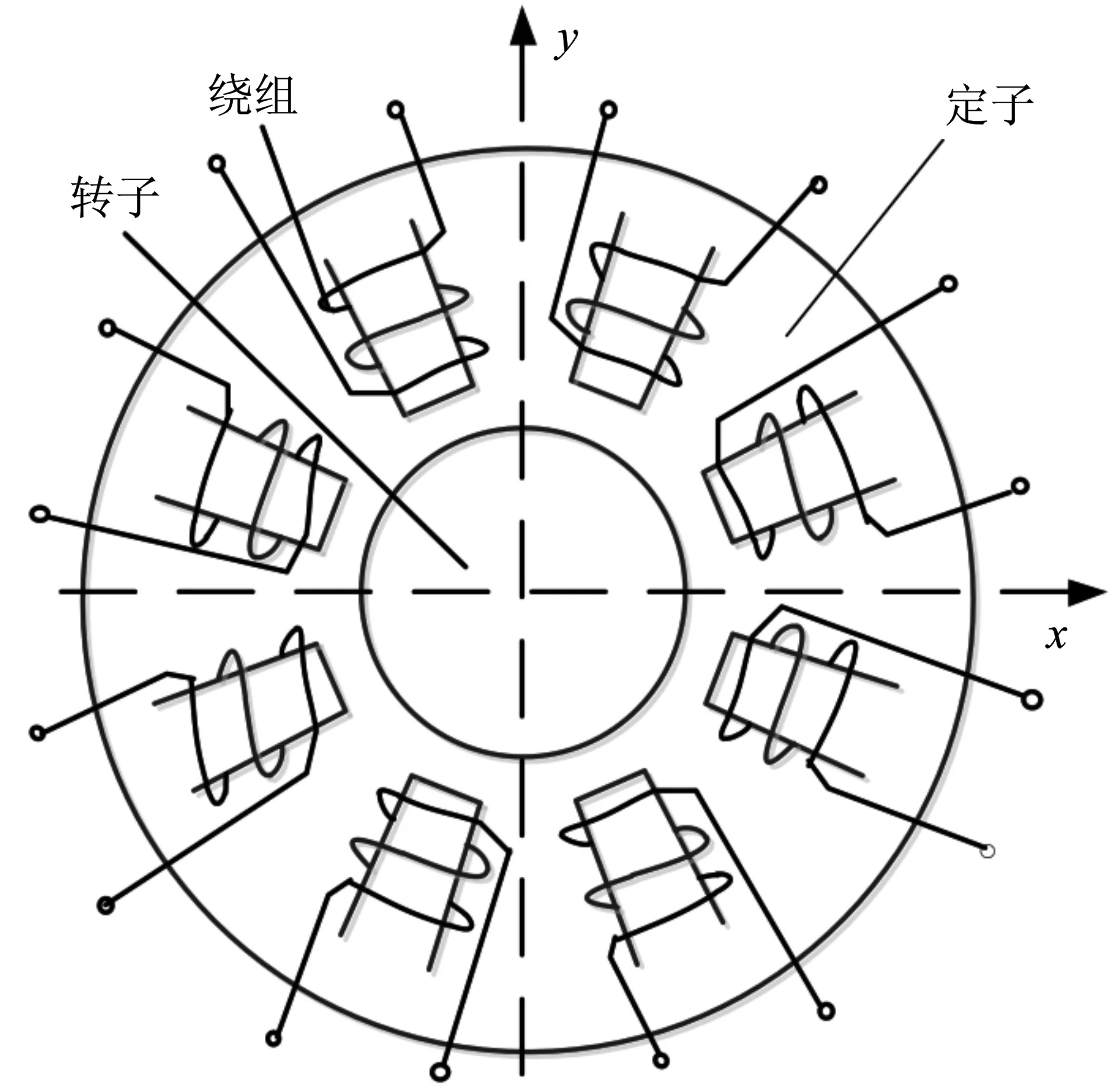
图2 8磁极独立驱动结构Figure 2. 8-pole independent drive structure
8磁极定子有3种磁极拓扑结构:全N(S)型、强耦合NSNS型以及弱耦合NNSS型,具体如图3所示。全N(S)型有大部分磁力线直接在空气中形成回路,磁路磁阻大,使得驱动电流转化为电磁力的效率较低,此种拓扑一般不采用。NSNS型与NNSS型相比,因为本文的“磁通等效”方法是利用磁极间磁路耦合实现容错控制,故本文以下分析采用强耦合NSNS型磁极拓扑结构。根据本文前期研究的数据分析,强耦合NSNS型的容错性能优于弱耦合NNSS型。

(a)
本文主要研究单个磁极回路故障情况,以磁通等效方法达到容错控制的目的。对于两个或两个以上磁极故障,理论上只要能在磁极端面构成磁通回路,用磁通等效是可行的,后续会展开相应的研究与验证工作。
2 电磁轴承磁极回路故障容错控制
2.1 电流-磁通影响系数法
根据麦克斯韦方程推导出单个磁极对转子的电磁力为
(1)
式中,μ0表示真空中的磁导率;A表示定子的有效横截面积;N表示磁极线圈匝数;I表示磁极驱动电流;X表示定子与转子间的气隙宽度。
式(1)中电磁力与电流是非线性关系。在考虑磁路耦合、漏磁等因素情况下,在实际中较难获得上式参数的数值,进而难以得到电磁力与驱动电流的精确对应关系,不利于提高控制精度。因此,本文提出磁通等效算法,当磁极通电后,其产生磁通大小与驱动电流成线性关系,且不仅在本磁极内产生磁通,还会对周边磁极也产生耦合磁通。在线性范围内,8个磁极同时通电运行产生的磁通分布等于各个磁极单独通电产生磁通的叠加,即满足叠加性。磁通比电磁力更容易描述磁极间的耦合问题。
磁通等效的算法任务就是为保持故障前后各个磁极端面上产生的磁通不变,重新计算出分配8个磁极所需的驱动电流,故障磁极电流为0。本文采用电流-磁通影响系数来描述驱动电流与磁通之间的关系。
为简化计算,做出以下假设与简化:
(1)忽略定子与转子铁芯的漏磁现象;
(2)忽略涡流效应;
(3)不考虑铁磁材材的磁饱合特性;
(4)不考虑边缘效应。
假设定子磁极回路通电时,各个磁极工作电流为I,各磁极的有效磁通为φ,有
MI=φ
(2)
式中,M矩阵就是电流-磁通影响系数矩阵,每个影响系数aij表示第i个磁极的驱动电流在第j个磁极处产生磁通的关系系数。
2.2 电流重分配矩阵
假设8磁极电磁轴承的1号磁极回路发生故障,如图4所示。
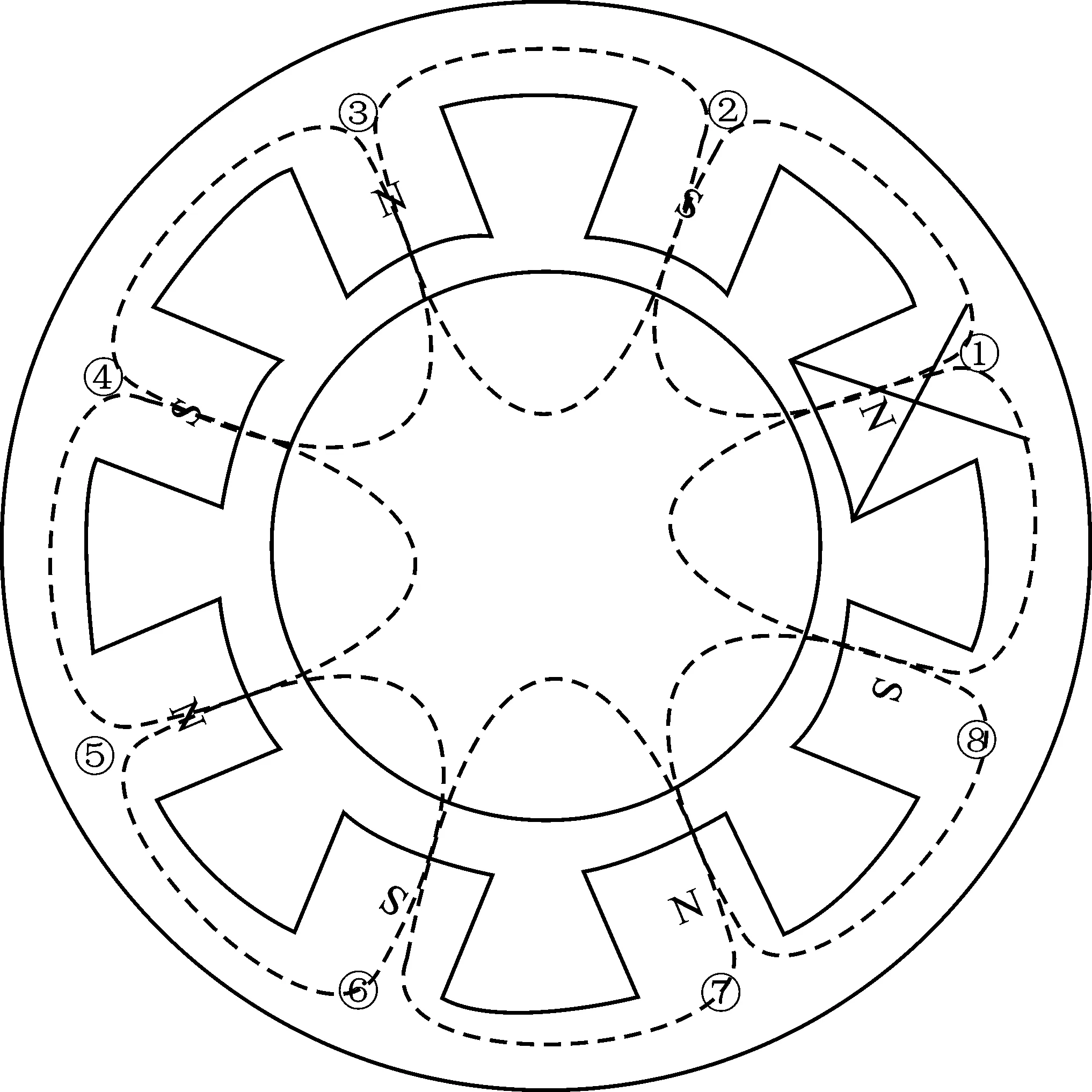
图4 磁极回路故障图Figure 4. Magnetic pole circuit fault diagram
如果希望故障前后各个磁极端面的磁通保持不变,则有
MI1=φ
(3)
将式(2)与式(3)比较可知,M矩阵和φ矩阵相同,I为已知,求解I1,即重新分配后的驱动电流。I1=[ 0i2i3i4i5i6i7i8],1号磁极故障,电流为0。
由(3)可计算得出如下等式
(4)
由式(4)可知,已知1号磁极故障,求解7个正常磁极驱动电流产生8个磁极的磁通,并且磁通与故障前相同。故障磁极电流已知为0,由8个方程求解7个未知数。
在线性代数中,方程个数大于未知数个数的方程组称为超定方程。以超定方程理论解释这个电磁轴承的方程组,要解出7个驱动电流,只需从7个方程的约束求解;多余的方程为多余条件,反而不能求解。因此,超定方程没有精确解,只有近似解。在电磁轴承方程中,可理解为用7个磁极产生最接近期望值的8个磁极的端面磁通。
先分析超定方程有最小二乘解的有解条件。根据超定方程最小二乘解定理:形如Ax=b有最小二乘解的充分必要条件为ATx=ATb有解。方程两侧都乘以AT,A当矩阵的列向量线性无关并且ATA是可逆矩阵,则方程ATAx=ATb有解,Ax=b有最小二乘解。
将式(4)转化为
KI′1=φ
(5)
式中,I′1=[i2i3i4i5i6i7i8]T;K是M矩阵去除故障磁极列系数后的子矩阵,为8×7矩阵。因为K矩阵为电流-磁通影响系数,列向量线性无关并且KTK是可逆矩阵,因此式(5)一定有最小二乘解。
基于上述定理可将式(5)可转化为
KTKI′1=KTφ
(6)
将式(3)带入式(6)化简可得
(7)
式(7)表示把故障前8个磁极的电流,为实现磁通等效容错控制,重新分配驱动电流的变换矩阵。W为电流重分配矩阵。
W=(KTK)-1KTM
(8)
3 算例分析
3.1 算例分析方案
在ANSYS仿真平台上搭建了8磁极独立驱动的NSNS型电磁轴承仿真模型,模型参数为本文实验室电磁轴承实验台实物数据,如表1所示。
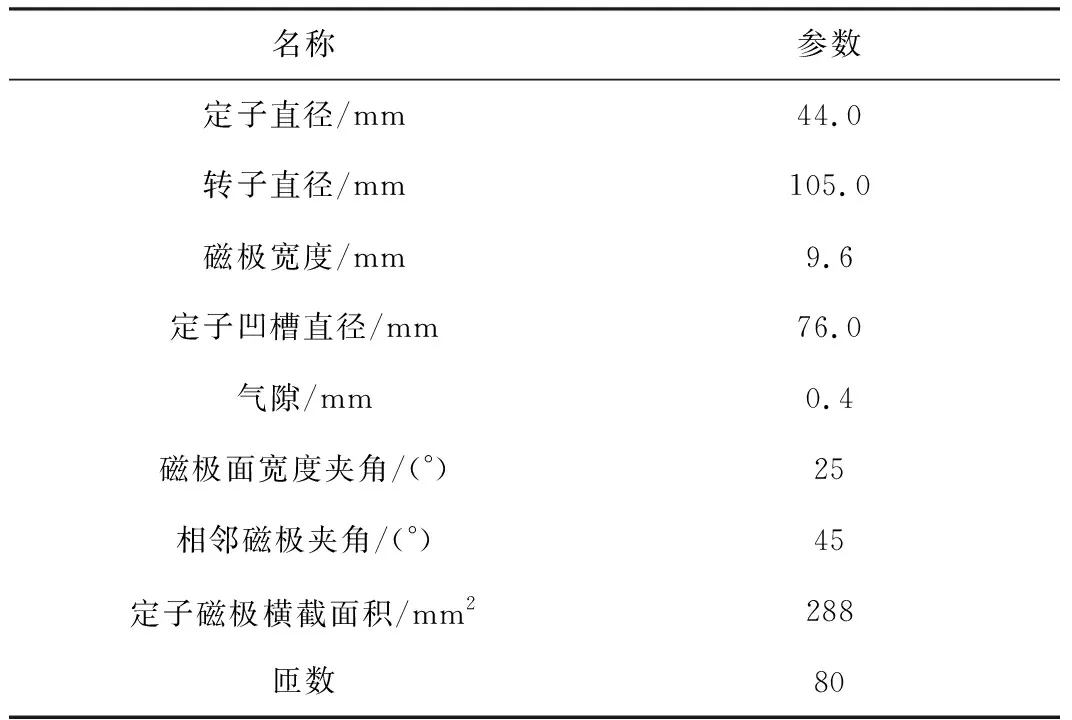
表1 模型参数表
电磁轴承磁极电流由偏置电流和控制电流叠加而成。偏置电流为所有磁极加载相同电流,能使电磁轴承的非线性支承特性工作在合适工作点,由控制电流产生期望的电磁力。在线性范围内,磁通和电磁力都满足叠加性。因此,以下算例分析从偏置电流和控制电流两个方面,分别检测和评价在容错前后磁极端面磁通、磁力线分布、控制电流形成磁通的等效性能。
3.2 偏置电流形成的端面磁通
本测试将在不同的偏置电流下,评估发生磁极故障后磁通等效的效果,4组算例电流分别为3 A、5 A、8 A、10 A。故障前各个磁极端面磁感应强度相同,发生故障后,磁极端面磁感应强度发生变化,故障磁极端面磁感应强度大幅减少。在实现“磁通等效”后,端面磁感应强度基本恢复到故障前。

图5 3 A故障前磁感应强度Figure 5. Magnetic induction intensity before fault at 3 A
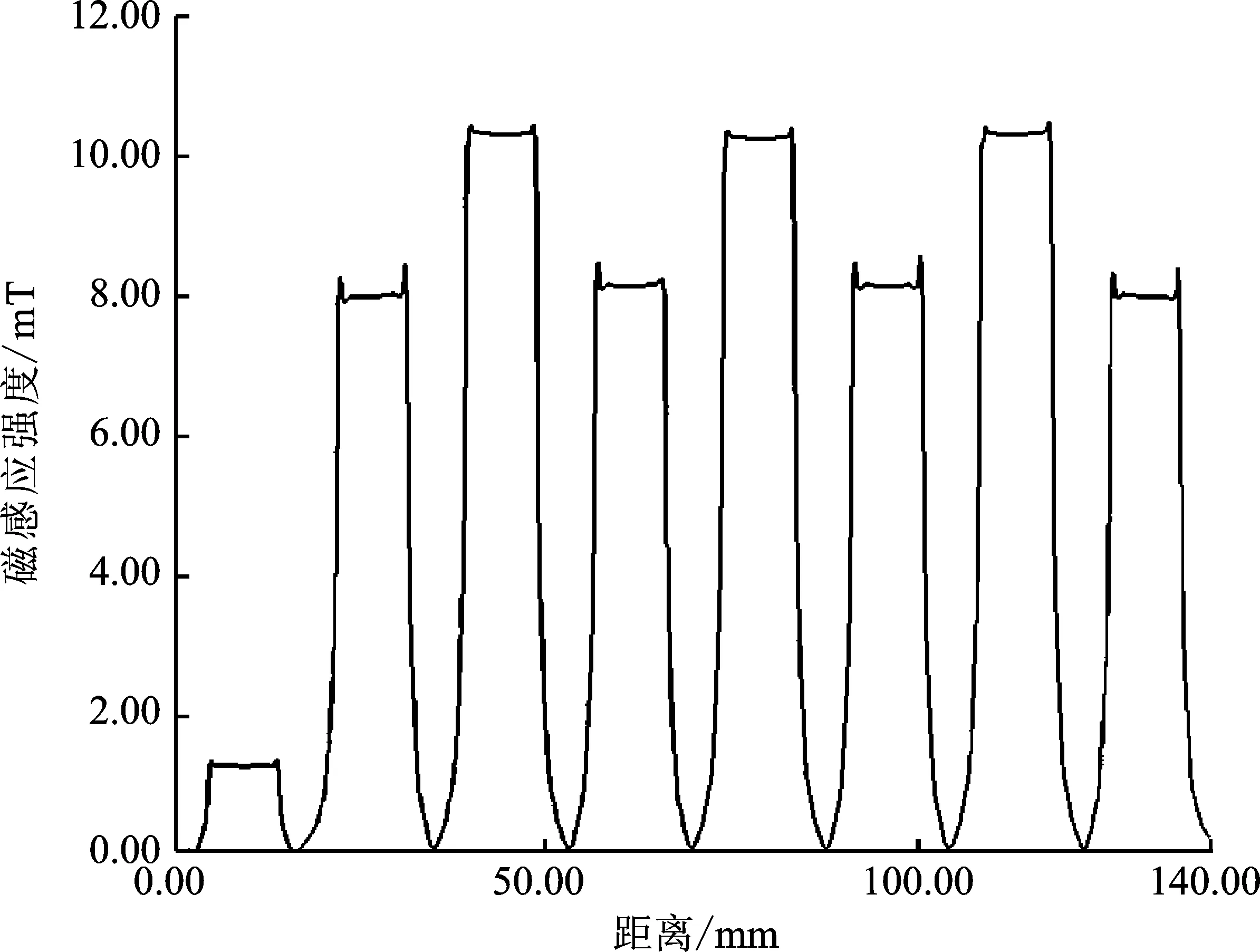
图6 3 A故障后磁感应强度Figure 6. Magnetic induction intensity after fault at 3 A

图7 3 A等效磁感应强度Figure 7. Equivalent magnetic induction intensity at 3 A

表2 激励电流为3 A时重新分配的电流值
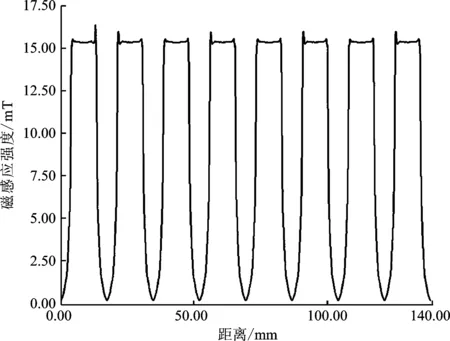
图8 5 A故障前磁感应强度Figure 8. Magnetic induction intensity before fault at 5 A
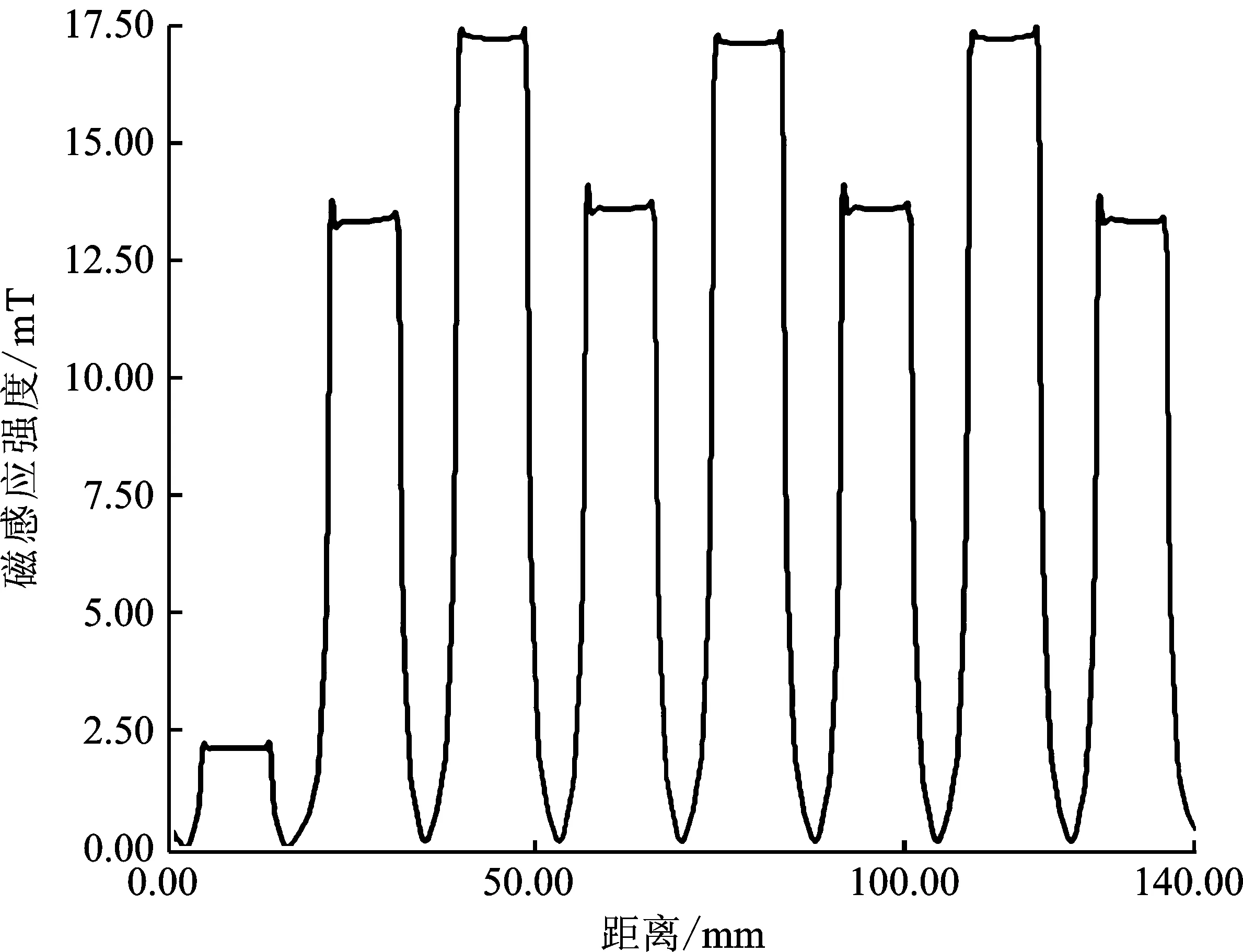
图9 5 A故障后磁感应强度Figure 9. Magnetic induction intensity after fault at 5 A
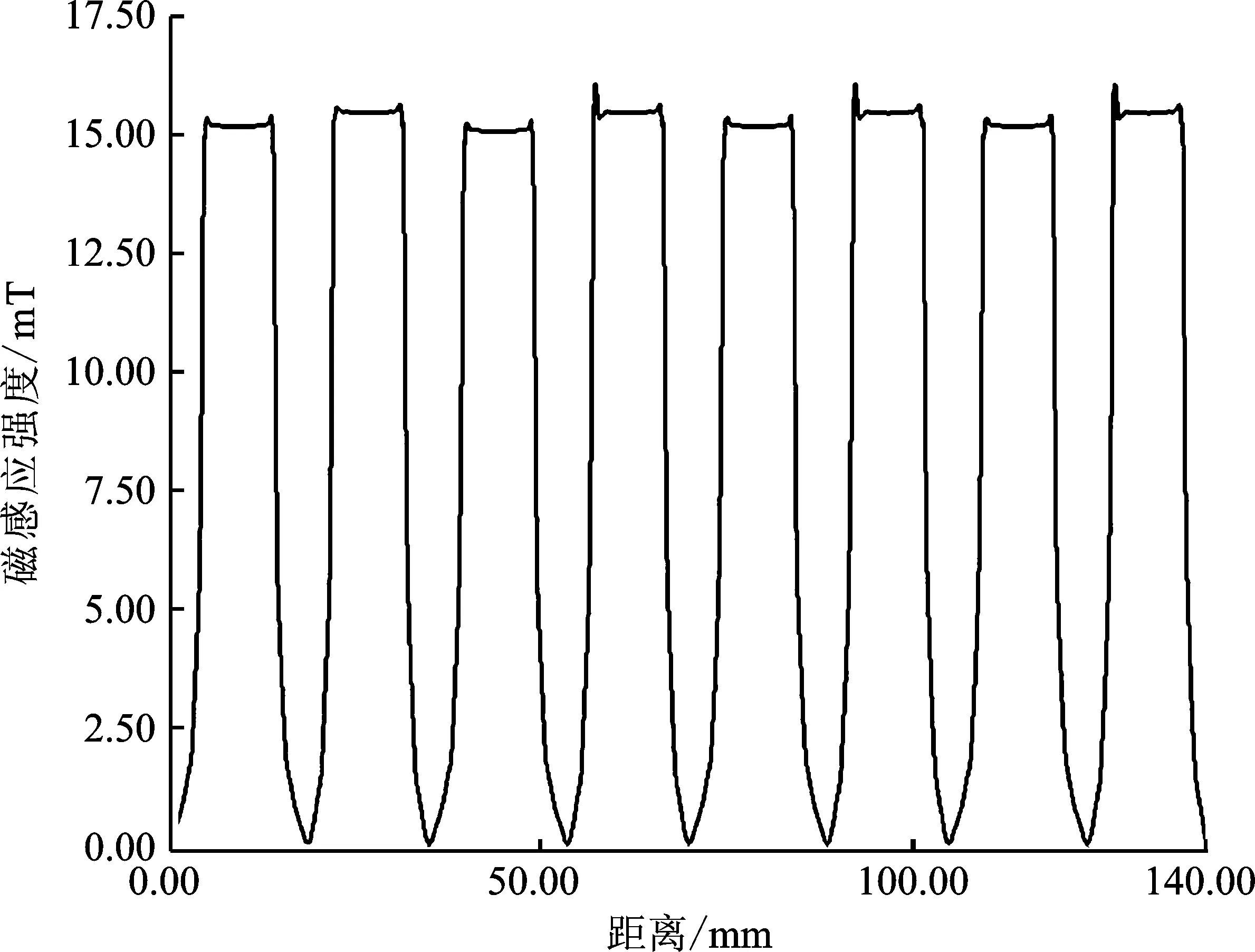
图10 5 A等效磁感应强度Figure 10. Equivalent magnetic induction intensity at 5 A
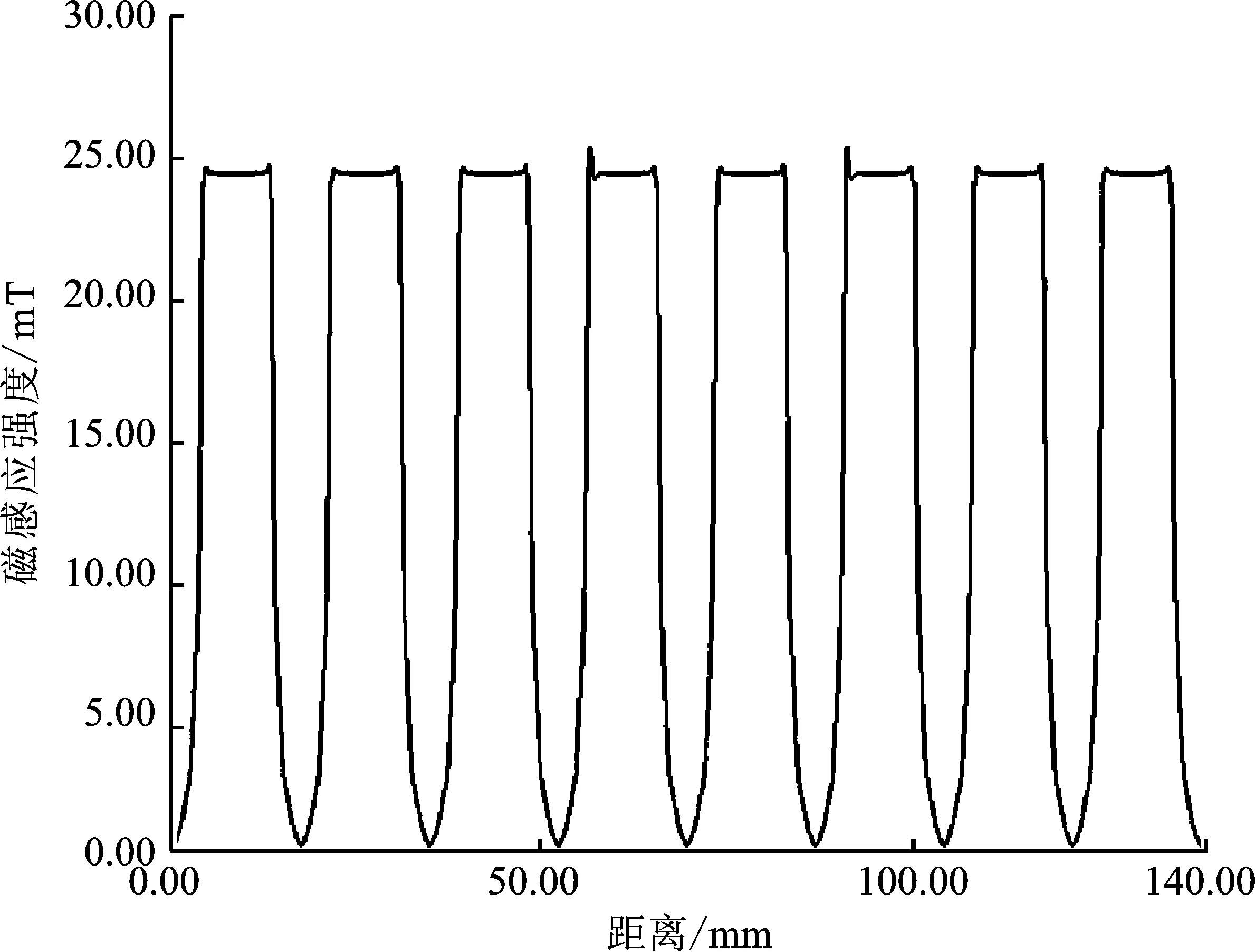
图11 8 A故障前磁感应强度Figure 11. Magnetic induction intensity before fault at 8 A

图12 8 A故障后磁感应强度Figure 12. Magnetic induction intensity after fault at 8 A
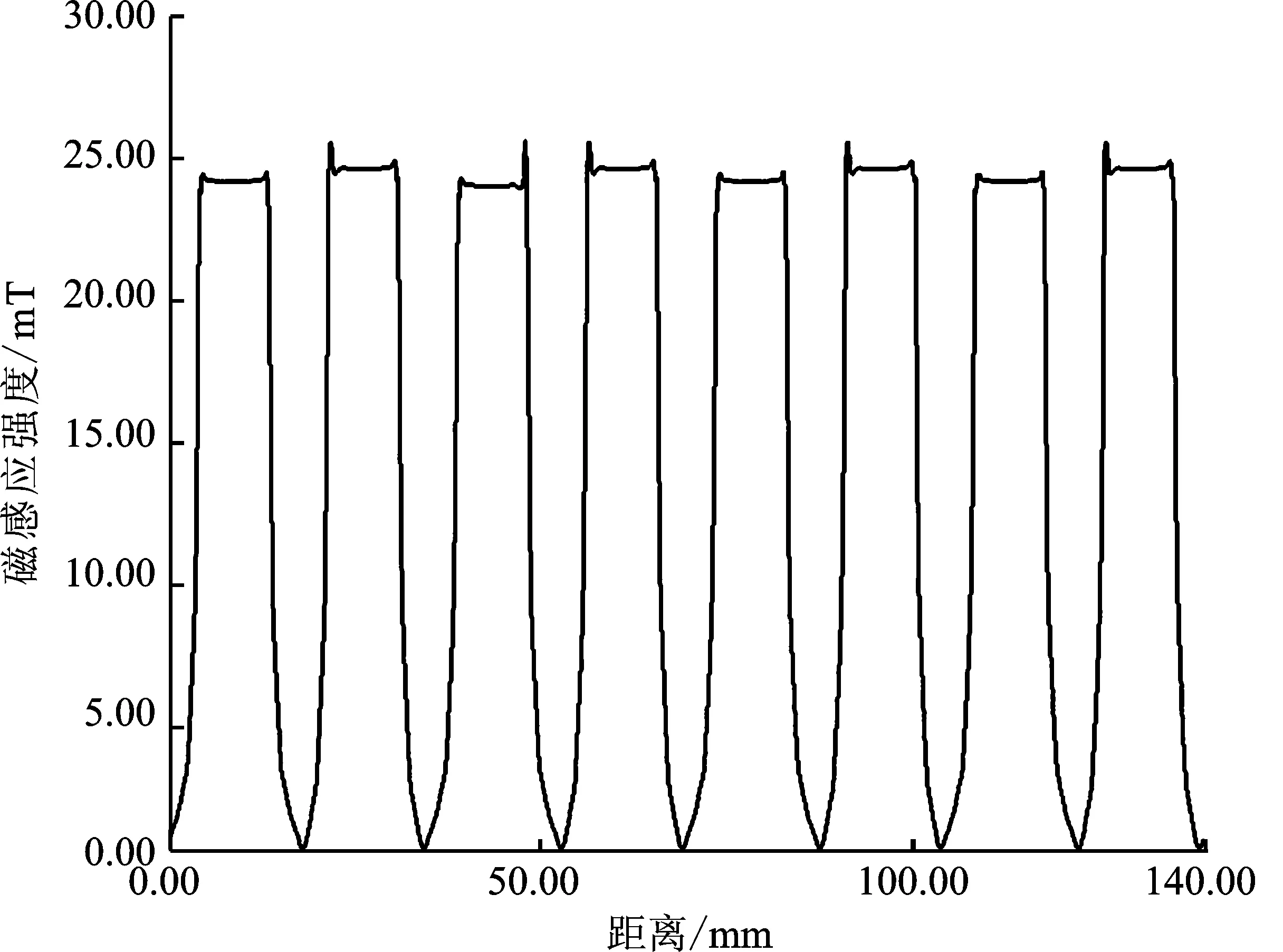
图13 8 A等效磁感应强度Figure 13. Equivalent magnetic induction intensity at 8 A
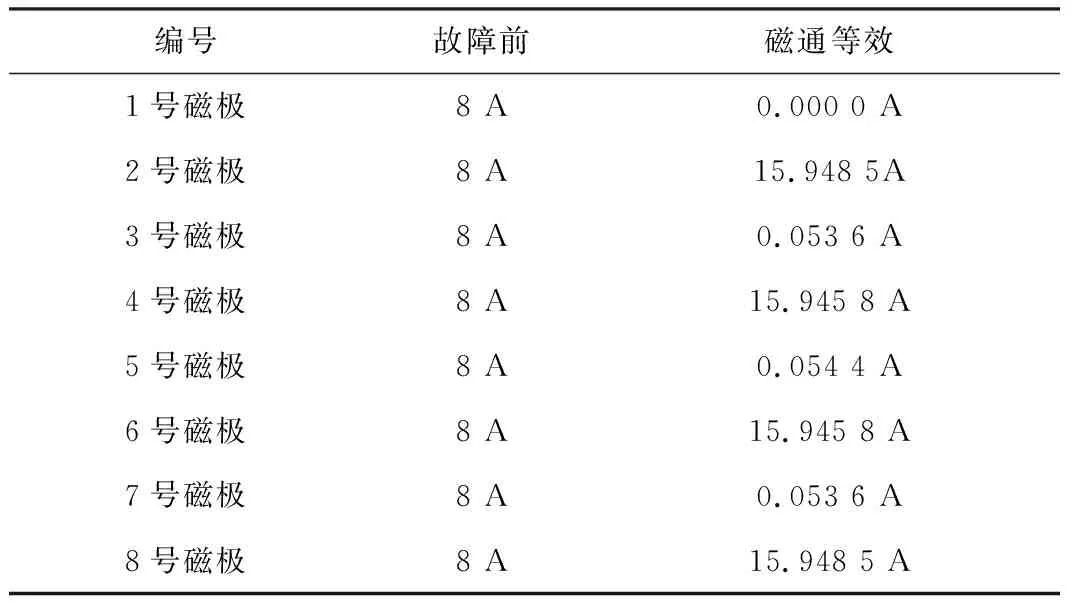
表4 激励电流8 A时重新分配的电流值

图14 10 A故障前磁感应强度Figure 14. Magnetic induction intensity before fault at 10 A

图15 10 A故障后磁感应强度Figure 15. Magnetic induction intensity after fault at 10 A
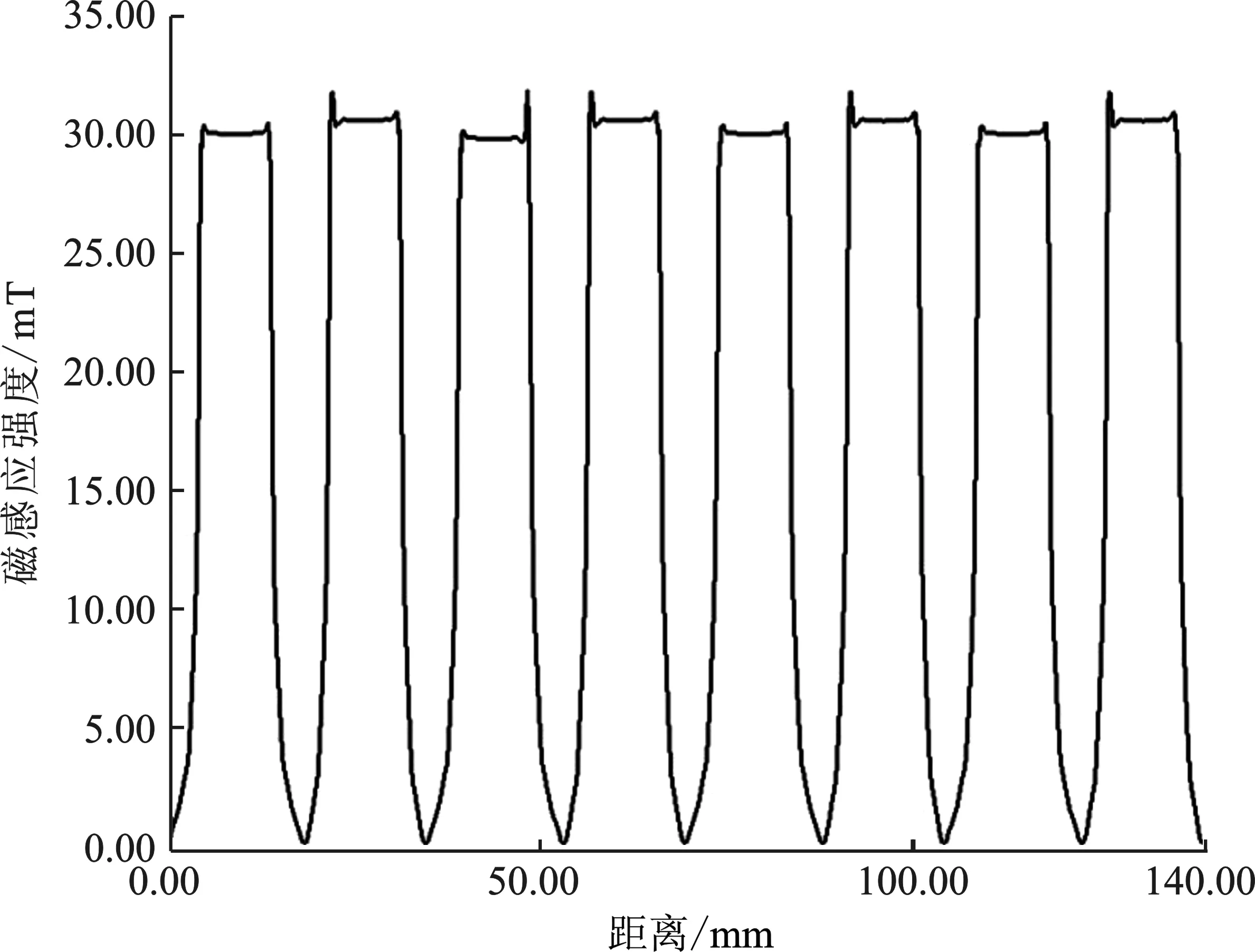
图16 10 A等效磁感应强度Figure 16. Equivalent magnetic induction intensity at 10 A
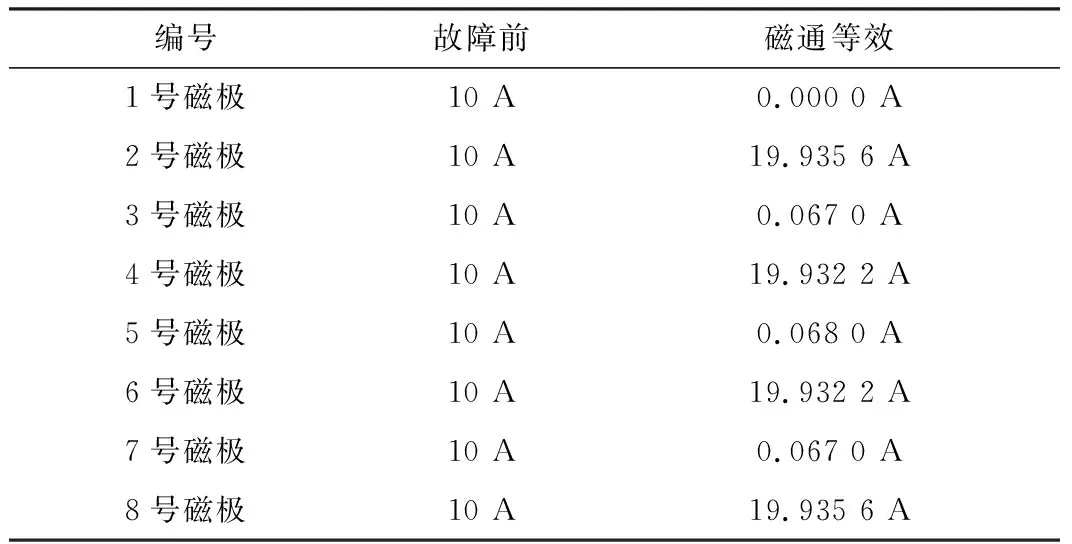
表5 激励电流10 A时重新分配的电流值
3.3 偏置电流形成的磁力线分布
本算例将分析故障前后及经磁通等效后的磁力线分布变化。当无故障时,激励电流5 A磁力线分布如图17所示。每个磁极端面磁力线分布均匀,相邻磁极磁力线成蝶状环型。

图17 故障前磁力线图Figure 17. Magnetic line diagram before failure
假设1号磁极回路发生故障,磁力线分布如图18所示。磁力线分布变化较大,故障处磁力线稀疏,且磁力线分布不均匀。
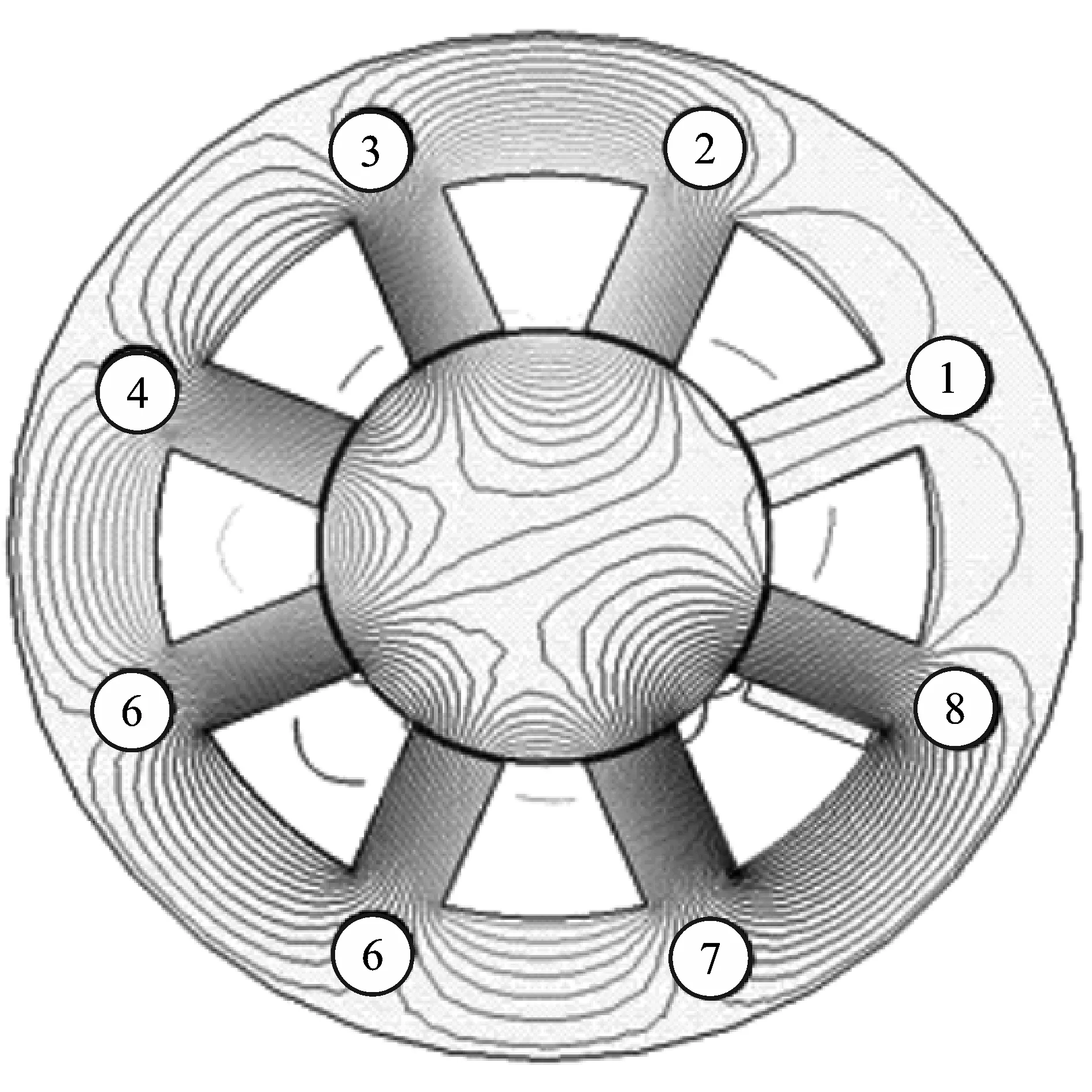
图18 故障后磁力线图Figure 18. Magnetic line diagram after failure
图19为使用磁通等效方法后得到磁力线分布图。由图可见磁力线已经基本恢复了故障前分布,因此使用磁通等效方法可以较好地还原故障前的磁力线分布。
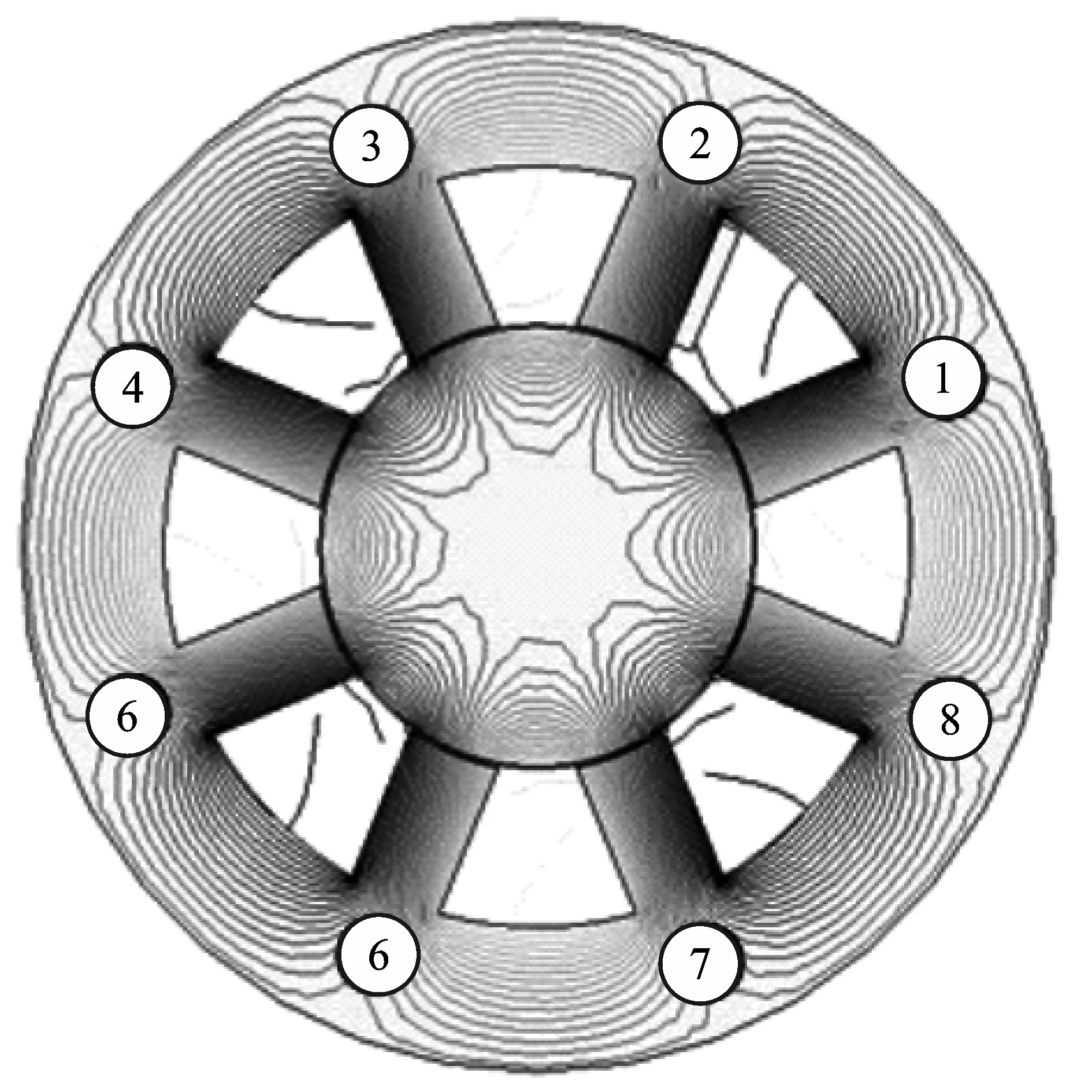
图19 磁通等效磁力线图Figure 19. Magnetic flux equivalent magnet line diagram
3.4 控制电流形成磁场的等效误差
根据前文分析,利用线性代数的理论,解出超定方程的最小二乘解。在理论上超定方程的解就存在误差,只是以最小二乘为原则,解得了最接近理想值的解。下文将重点分析超定方程解的误差对本文提出方法磁通等效效果的影响。
以在传统差动磁极驱动条件下,产生二维平面内任意X轴Y轴±100 N内组合的力所对应8个磁极端面的磁通值为等效对象,计算平面内所有情况的磁通等效误差。
磁通等效误差的计算过程如下,在二维平面内的一个任意力,先求出其差动驱动且磁极无故障时8个磁极的磁通φ1。再假设1号磁极故障,通过磁通等效重新分配电流后的8个磁极的磁通φ2。
(9)
(10)
最后,对应8个磁极的端面磁通的误差,取最大的相对误差。
(11)
在X轴Y轴±100 N的平面内,以1 N为间隔进行计算。对于二维平面上的每个力,得到磁极故障前后的磁通等效误差如图20所示。
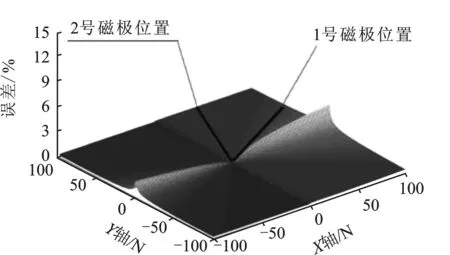
图20 1号磁极故障前后的磁通等效误差图Figure 20. Equivalent error diagram of magnetic flux before and after No.1 pole fault
由图20可知,X轴和Y轴为电磁力平面,纵轴表示该点力的磁通等效误差。假设1号磁极损坏,在如图标记位置。由图可知,在X轴Y轴±100 N的平面内,大部分地方(图中较平坦的地方)的磁通等效误差较小,在0.5%以内,误差峰值出现在X轴上。误差值沿X轴呈山脊状,最大误差出现在(100 N,0)处,误差值为3.2%。
与预想不同的是,图20中最大误差没有出现在故障磁极的位置,而是出现在离故障磁极最近的坐标轴上,即X轴上。这可能是因为本文的磁通等效是以差动驱动的磁通为期望值,而差动驱动产生坐标轴方向的力,只涉及该坐标轴方向磁极,不牵涉其他方向磁极的耦合电磁力,导致等效精度降低。
本文又对假设2号磁极损坏的磁通等效误差数据进行了分析,如图21所示。由图可知,最大误差仍然出现在离故障磁极最近的坐标轴上,即Y轴。
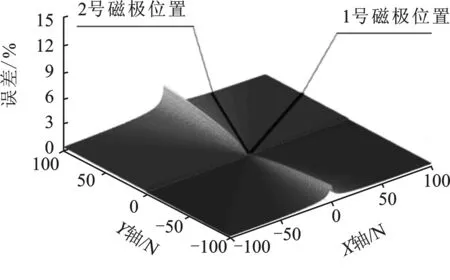
图21 2号磁极故障前后的磁通等效误差图Figure 21. Equivalent error diagram of magnetic flux before and after No.2 pole fault
由于在电磁力是矢量,重构电磁力在方向上存在夹角,故将电磁力正交分解于X、Y轴进行误差分析。由上述重构电流计算出磁极电磁力,得到如下所示电磁力误差图。

图22 Y轴方向力误差图Figure 22. Y-axis direction force error diagram
由图22可知,将等效后的电磁力正交分解于X轴上,平面大部分区域误小于2%,最大误差出现在(100 N,0)处,误差值为7%。
由图23可知,将等效后的电磁力正交分解于X轴上,平面大部分区域误小于2%,最大误差出现在(100 N,0)处,误差值为7%。

图23 X轴方向力误差图Figure 23. X-axis directional force error diagram
4 结束语
针对电磁轴承运行时有可能发生的磁极回路故障导致转子悬浮失控的问题,本文提出了以定子磁极端面的有效磁通不变为控制目标的容错方法。通过ANSYS平台仿真结果分析,可以得到如下结论:
(1)某个磁极回路发生故障后,本文提出的以“磁通等效”为原则的容错方法能够通过对定子磁极电流的重新分配,利用其他正常磁极产生耦合磁通,使8个磁极端面的磁通在故障前后保持不变。磁通环境相同,电磁力也自然相同,实现容错运行;
(2)在磁通等效中,对偏置电流在磁极故障发生后,磁极端面磁感应强度和定子整体的磁力线分布可以基本恢复到故障前的正常情况。
(3)磁通等效中,控制电流最大误差出现在离故障磁极最近的坐标轴上,当力为100 N时,最大磁通误差值为3.2%,最大力误差为7%;平面上大部分地方的磁通误差小于0.5%,力误差小于1.5%。
