最早截止期优先算法在CAN FD网络中的改进
2023-01-04管银凤张凤登张海涛张宇辉
管银凤,张凤登,张海涛,张宇辉
(上海理工大学 光电信息与计算机工程学院,上海 200093)
随着新型汽车产业的发展,汽车上的电子控制装置数量急剧增加,众多传感器和执行器之间进行通信传输的信号量也大幅度增多,导致传统的CAN(Controller Area Network)总线已无法完全满足新型汽车产业对通信总线的要求[1]。CAN FD(CAN with Flexible Data rate)总线的带宽大,其传输速率可达CAN总线的3~8倍,且能够降低错误帧漏检率,将会成为今后汽车电子领域的一个重要研究方向[2-4]。与此同时,为了保证传感器与执行器之间信号量传输的实时性,采用合适的调度算法对众多信号量进行快速、高效地调度,对汽车系统的安全及稳定起着至关重要的作用[5]。因此,利用CAN FD总线来快速、准确、实时地传递信息,对汽车内信息进行调度的研究具有重要的意义与价值[6]。目前基于优先级的调度算法大体可分为静态调度、动态调度和混合调度等[7]。其中,静态算法包括单调速率调度算法(Rate Monotonic,RM)和截止期单调调度算法(Deadline Monotonic,DM)[8]。然而这两种算法均对总线利用率较低且对事件触发的报文处理不够灵活[9]。动态算法包括最早截止期优先算法(Earliest Deadline First,EDF)和最小松弛优先算法(Least Laxity First,LLF)[10],这两种算法分别以消息的截止时期和剩余时间长短来分配任务优先级,提高了网络的利用率。为了适应不可抢占任务的需要,文献[11]给出了不可抢占式EDF调度算法的可调度性判定方法。文献[12]提出了一种分解算法来对应用在多核处理器上的最早截止期优先算法进行优化。文献[13]通过使用调度技术减少了网络引起的延迟,确定了CAN、以太网、TDMA(Time Division Multiple Access)以及F-DMA(Frequency Division Multiple Access)之间适合用于EDF调度的PID(Proportional Integral Derivative)控制网络,并通过该算法减少了时延问题。文献[14]中将EDF算法和LST(Least Slace Time First)算法相结合,提高了实时任务的调度性能。文献[15]对编码动态更新和优先级反转的问题提出了优化方法。其通过利用EDF算法来提高消息的实时性,且解决截止期编码问题时,可以采用不同的分区编码方式把变化范围较大的截止期表示出来[16-17]。在综合考虑截止期和价值度两方面影响后,文献[18]提出了基于截止期价值度优先的DVF(Deadline Value First)算法,即在满足消息的截止期的前提下,尽量让价值度更高的消息优先发送。
本文在对平均分区EDF调度算法研究的基础上,改进了适用于CAN FD通信的EDF调度算法。利用指数-幂函数的动态编码分区方法扩大了截止期的编码范围,降低了出现优先级反转的概率,并合理分配了网络带宽,降低了总线负载,适当提高了带宽利用率。
1 EDF算法
1.1 平均分区EDF算法
为了提高单处理器系统的处理器利用率,EDF算法是动态抢占式调度算法中非常重要的算法[19]。该算法根据报文的绝对截止时间Dm的大小动态分配优先级。报文的绝对截止时间越小,其优先级越高。然而随着时间的增加,报文的绝对截止时间也随之增大,此时标识符的表示范围将无法涵盖所有的截止期。因此,为了有效地减少标识符ID(Identifier)中用来表示优先级的位数,本文引入相对截止时间dm=Dm-tstart,其中tstart为总线仲裁开始时间。此外,通过对报文的截止时间进行编码来计算报文的优先级,而采用不同的标识符编码方式得出的优先级计算结果也会相应不同,通常在EDF算法中采用如下所示的平均分区编码方式。
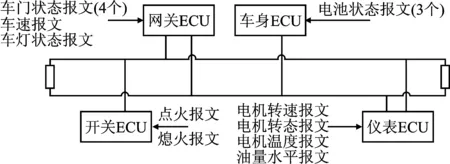
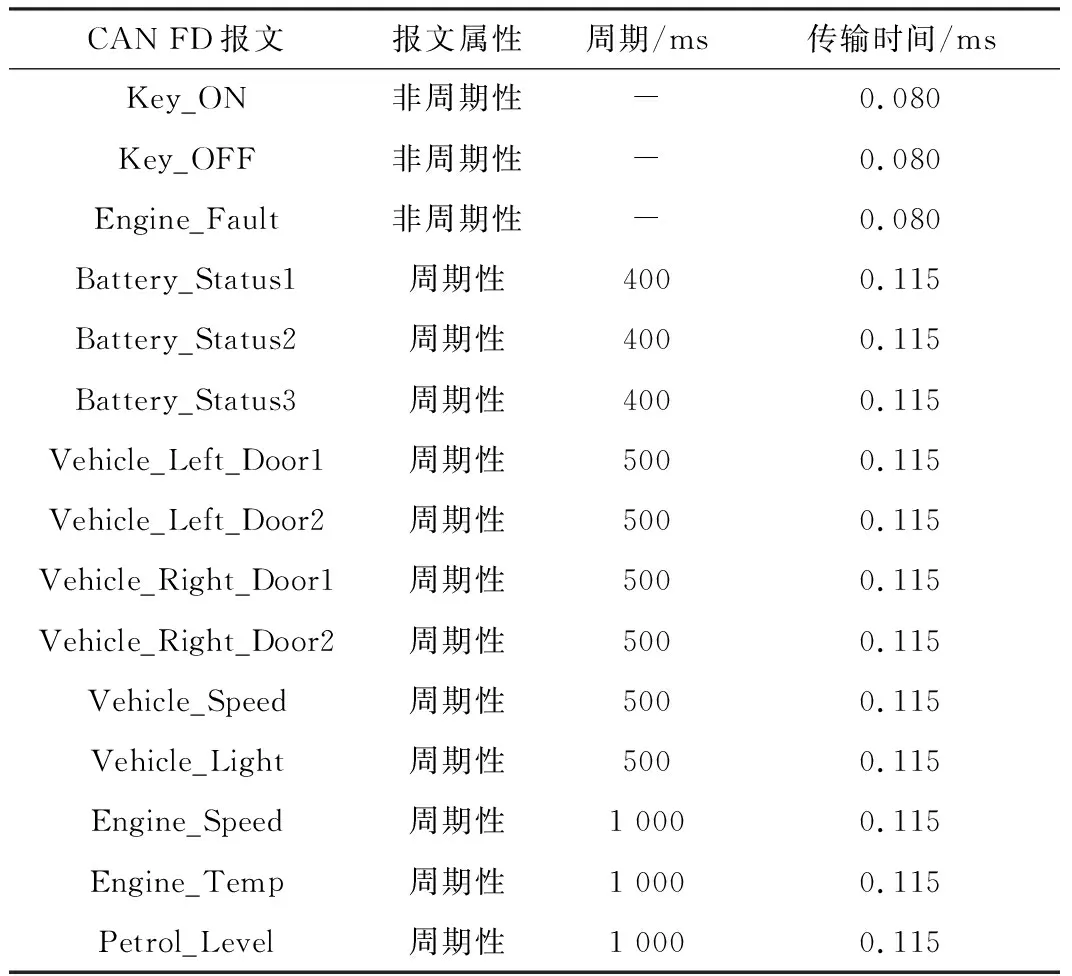
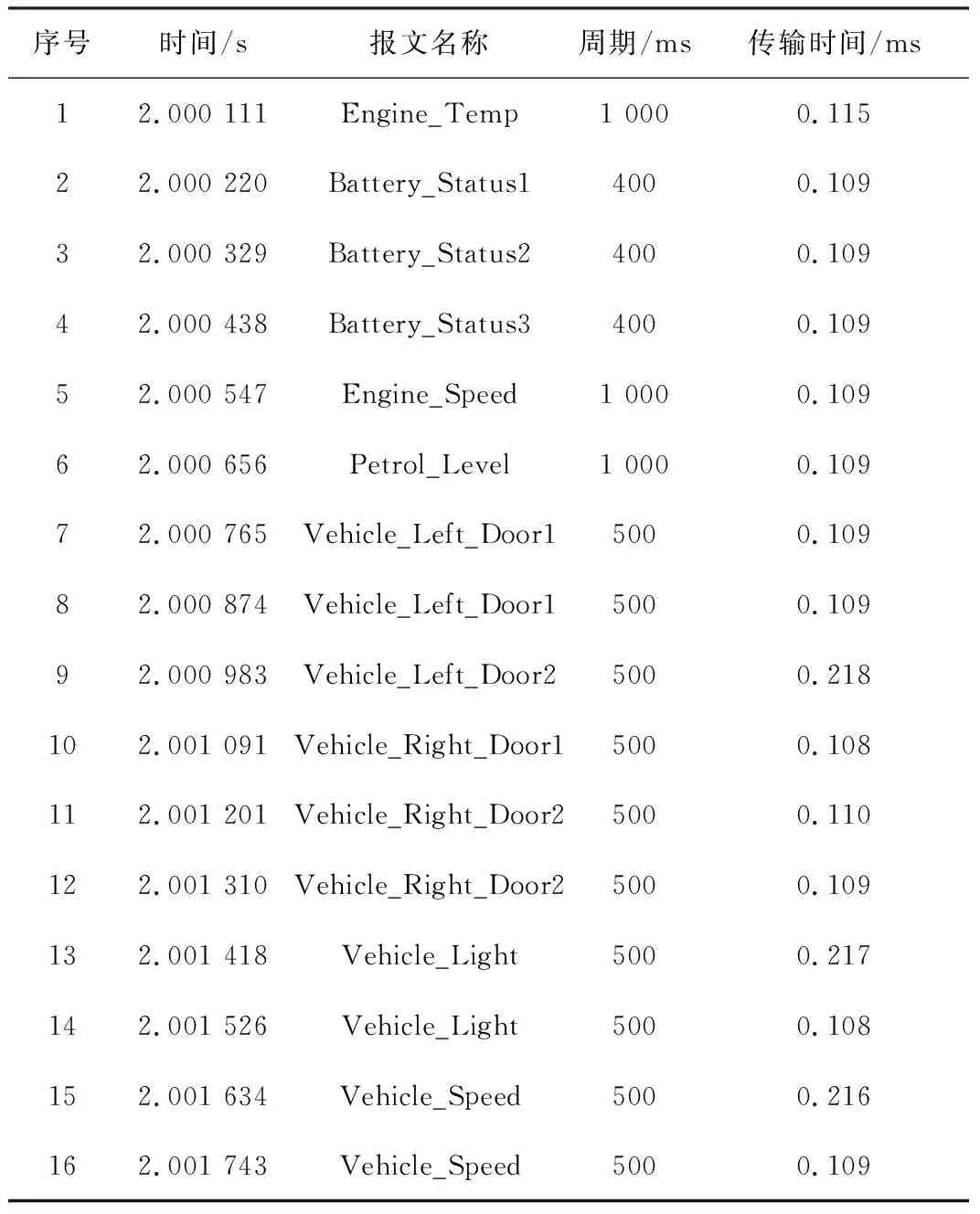
对于一组报文{m1,m2,…,mn},假设它们的相对截止时间从小到大排列为{d1,d2,…,dmax}。采用平均分区的方式是将时间轴以报文的最大相对截止时间dmax为上限等分成k段,则每段区间长为dmax/k。假设对任意两个报文mi与mj,其相对截止时间分别为di与dj且di 图1 平均分区示意图Figure 1. Schematic diagram of average partition 根据EDF调度算法,在每轮调度时,报文的优先级根据其相对截止时间确定。图1中报文mi与mj的相对截止时间di与dj被划分在一个区间,即二者具有相同的优先级。这与根据标识符判定mi的优先级高于mj的实际情况不符。因此,根据上述分区,会导致报文mi被mj推迟占用总线的优先级反转问题[20]。 由于CAN FD总线属于非抢占式总线,故参考信号调度中非抢占式调度理论对报文的可调度性判定进行分析。首先给出定理1,以确保总线利用率满足要求,接着用定理2给出非抢占截止期调度策略的可调度性判定。 定理1[11]由n个报文组成的报文集合{m1,m2,…,mn},当且仅当在所有报文均满足式(1)时,则称其为可调度的 (1) 式中,Cm和Tm分别为报文m的传输时间和请求周期。 定理2[11]对实时任务τm=(Tm,Cm,dm),m=1,2,…,n,当且仅当其满足以下计算式时,非抢占截止期调度策略是可调度的 (2) 式中,dmin=min{dm:1≤m≤n};Cp代表报文所需的最长通信时间。 上述两个定理成立的条件已在文献[19]中得到证明。为了简化判定条件,假设报文传输在最坏情况下(即最坏的阻塞情况)发生,所有报文在同一时间t=0时释放。由于任务执行时是非抢占的,即此时无论请求执行的新任务的优先级高低,正在执行的任务都无法被中断,而新任务则必须在该任务执行结束后才有机会使用总线。针对上述情况,可调度性的判定应将高优先级报文被低优先级报文阻塞的时间包含在内,如引理1所示。 引理1[21]假设由n个报文组成的报文集合{m1,m2,…,mn}。该消息集合在满足式(3)时,可被EDF算法调度 (3) 式中,Cm、Tm、Bm分别为报文m传输时间、周期及最大阻塞时间。 针对指数分区的方式,若使接近仲裁开始时间的区间较小,则精度会增高;而离仲裁开始时间远的区间较大,精度也会有所降低。因此,在这种分区方式下,能够在较大程度上减少截止期相近的两个报文被分到同一个母区间内的概率,从而更好地保证报文的实时性[16]。本文对母区间采用指数分区的方式,其具体过程如下: 步骤1将报文集合中的各相对截止期dm按大小排列,取截止期中的最大值dmax作为截止期分区的上限值; 步骤2选取指数分区时的分区因子a,即采用以a为底的指数方式对相对截止时间范围[0,dmax)进行分区时,首先需要明确底数a的大小。由于分区因子a的大小和报文的数量有关,在本文中为了计算简单清晰故取a=2; 步骤3根据上述的指数分区方案,假设报文在0时刻释放,将以0时刻为起始至dmax/2k的范围定义为母区间0,则共计k+1个母区间,以{I0,I1,I2,…,Ik-1,Ik}形式表示,即分区后第1个母区间I0的范围为[0,dmax/2k),第2个母区间I1的范围为[dmax/2k,dmax/2k-1)。以此类推,第i个指数分区Ii的范围为[dmax/2k+1-i,dmax/2k-i),最后1个母区间Ik的范围为[dmax/2,dmax)。综上,其区间范围表示为 (4) 则第i个母区间的大小如式(5)所示。 (5) 母区间具体划分如图2所示,按照上述方法划分出多个母区间,且各个母区间的长度均不同。这种分区的优点是能在一定程度降低截止期相近的报文在传输时分配同一优先级的可能性,可以有效避免优先级反转的情况出现。 图2 母区间指数分区Figure 2. Parent interval of exponential function partition 在采用指数函数将截止期分成多个母区间后,本文将采用幂函数分区方式将每个母区间再细分成多个子区间。该操作的目的是再次在有限的范围内细分出不同长度的截止期区间,以便在满足不同报文的截止期要求的前提下,进一步降低优先级反转出现的概率。假设对每个母区间Ii按照幂函数的方法再划分出q个子区间,其中选取幂函数的幂次为1。图3中给出在第i个母区间中划分为q个子区间的分区情况。 图3 子区间幂函数分区Figure 3. Subintervalof power function partition 经过上述指数函数的分区后,在对每个母区间内划分子区间时,子区间的实际表示范围需要考虑到母区间的起始下限值。因此,在第i个母区间的第1个子区间的范围为[dmax/2k+1-i, (q+1)×dmax/q×2k+1-i),第2个子区间的范围为[(q+1)×dmax/q×2k+1-i,q×dmax/(q-1)×2k+1-i)。以此类推,即可得出第i个母区间的第j个子区间的范围为 (6) 式中,i=0,1,2,…,k;j=2,3…,q。第i个母区间的最后1个子区间的范围为[3×dmax/2k+2-i,dmax/2k-i)。 根据上式,将每个子区间称为基本时间单元U,则第i个母区间的子区间j可利用基本时间单元Uij表示,而Uij的大小可以根据式(7)求出。 (7) 经过分区编码后,现存网络中就有q×(k+1)个优先级的信息。假设CAN FD总线的标识符编码位共有n位,如果要涵盖所有的优先级则必须满足2n≥q×(k+1)。 假设所有报文的相对截止时间已知,且报文m的相对截止时间为dm,且dm≤dmax,则根据dm的大小及分区方式可以求出其所在的母区间和子区间,进而求出报文m所对应的优先级。具体计算过程如下所示: 步骤1先计算出dm所在的母区间的区间号i。任一报文的截止期按照此分区方式进行划分,必定位于划分的某个母区间范围内,即满足 (8) 式中,i=0,1,2,…,k。 根据上式,利用截止期dm所在的范围反求母区间i的范围,化简可得 (9) 由于优先级越高其所在区间号i应该越小。因此确定区间号时采用向下取整的方式以获得更高的优先级,此时求出i的值为 (10) 步骤2确定截止期dm所处子区间的区段号j。报文的相对截止期必定落在子区间j所处范围内,即 (11) 根据式(11)计算子区间区段号的大小,得 (12) 整理上式可得子区间区段号j为 (13) 步骤3根据计算式计算得到的母区间号i和子区间号j的值,随后即可计算报文的优先级p,至此完成将报文的绝对截止时间转化为报文优先级操作,计算式如下 p=j+(i-1)×q (14) 将求得的优先级p为十进制,可将其二进制化即为报文的标识符。 在采用上述指数-幂函数方式进行分区时,以各个报文的相对截止时间为基准,可以求得各个报文的优先级,进而完成对标识符的动态编码。然而,在计算优先级的过程中对母区段号和子区段号的选取均为向下取整,这种做法不可避免地会产生误差。将这种误差定义为“量化误差”[16,22],记该误差为Eij,式中,i=0,1,2,…,k;j=1,2,…,q,则其值为 (15) 根据上式中的误差Eij,可以进一步对EDF算法的可调度性判定引理1中的判别式进行修正,得到式(16),即 (16) 式中,Eij为正常传输过程中每个报文经计算存在的误差。量化误差Eij一定为正且其大小不会超过基本时间单元Uij的大小,即0 ≤Eij≤Uij。在此误差影响下,若要充分保证系统可调度,则可调度性判别式应更新为式(17),即 (17) 令Xf=Uij/Tm, 式中Xf≥0,f=1,2,…,k×q,化简上式得 (18) 若取X=max{Xf},则最终的可调度性判定式为式(19)。 (19) 通过上述的可调度性判别计算式可知,量化误差的存在对报文的可调度性产生了影响,使报文的可调度性判别更加严格。 为达到良好的仿真效果,以下将从通信网络定义、ECU(Electronic Control Unit)定义及报文、信号等层面详细进行网络分析规划。整个网络由以下4个可选用CAN FD总线传输的ECU组成[23],总计传输15个报文,具体为:(1)用于控制车载3个电池状态的BCM(Battery Control Management)ECU,共计收发3个报文;(2)用于实现数据在仪表盘上显示传送发动机速度、状态、温度及油耗的电机状态的IPC(Instrument Panel Cluster)ECU,共计收发4个报文;(3)用于控制车两侧的前后车门、车速、和车灯状态的Gateway ECU,共计收发6个报文;(4)用于收发点火与熄火的开关Switch ECU,共计收发2个报文。网络设计规划如图4,节点报文分配见表1。 表1 报文分配 图4 CAN FD网络规划设计Figure 4. CAN FD network planning and design 按照图4网络规划将信号加入数据库并搭建CANoe仿真实验平台,电机状态(仪表)ECU和Switch ECU所产生的报文设置为非周期性报文,而网关ECU和车身ECU均为周期性报文。电池状态报文周期为400 ms,车门状态相关报文及车速、车灯报文周期设置为500 ms,电机转速及温度与状态报文周期为1 000 ms。周期性报文传输时间设定为0.115 ms,非周期性报文为0.08 ms。设置报文释放时间为零,即假定报文的相对截止时间与其周期相等,按照指数-幂函数分区方式进行编码,并根据报文的初始相对截止时间计算报文的起始ID,具体参数设定如表2所示。 表2 报文及参数设定 为验证本文提出的方法的调度效果,分别对采用平均分区和指数-幂函数分区的EDF算法进行仿真实验。首先进行可调度判定,任意截取一段报文传输的具体数据如表3所示。表中第4列为报文的周期Ti,其最小值为400 ms;第5列为计算的报文传输时间,即式(2)中的Ci,本文此处以t=2.0 s时刻具体举例说明。 表3 t=2.0 s时传输报文的具体数据 对表3中截取t=2.0 s传输的报文数据按照定理2进行可调度性判定,即将所有Tm、Cm、dm、Cp数据带入式(2)进行计算。其中,最长传输阻塞时间Cp= 0.109 ms,则有 (20) 经过上式计算,满足定理2对于可调度性的判定,即传输的报文集是可调度的。 验证可调度后,采用该组报文集进行实验。为了对比实验,选定的报文传输速率分别为4 Mbit·s-1、8 Mbit·s-1,其中4 Mbit·s-1的波特率是Vector推荐的CAN FD的最佳传输速率。两种分区方式下的调度结果如图5和图6所示。 (a) (c) 根据仿真实验结果计算在不同波特率下各自的总线负载可得:(1)采用传输速率为4 Mbit·s-1下的指数-幂函数编码的总线负载为0.28%,而平均分区的总线负载为0.49%;(2)当传输速率为8 Mbit·s-1时,两者各自的总线负载分别为0.25%和0.43%。经计算,采用本文提出的指数-幂函数编码方法进行调度时,总线负载分别降低了42.90%和46.50%,表明本文对EDF算法的改进是可行的。此外,在传输速率为4 Mbit·s-1的仿真实验过程中,报文被阻塞的最大时间为1.317 ms,最大误差为31.25%。根据引理1可得 (21) 上式计算验证了系统是可调度的,这与仿真实验结果及定理2的判定结果一致。 本文在研究平均分区EDF调度算法的基础上,提出了使用指数-幂函数的分区编码方式改进EDF算法。经过仿真实验,验证了改进后的算法通过划分不同的母区间与子区间,使截止期各不相同的报文都能处在正确的区间内,不仅可以优化之前会出现的优先级反转问题,还能够有效降低总线负载。但是本文的不足之处在于,对报文调度进行的研究是假设系统处于一种理想状况,忽略了报文传输延迟、释放抖动以及传输时可能出错的情况,从而存在一定误差。日后可针对这种不足做出改进,并可以搭建硬件节点进行实物验证。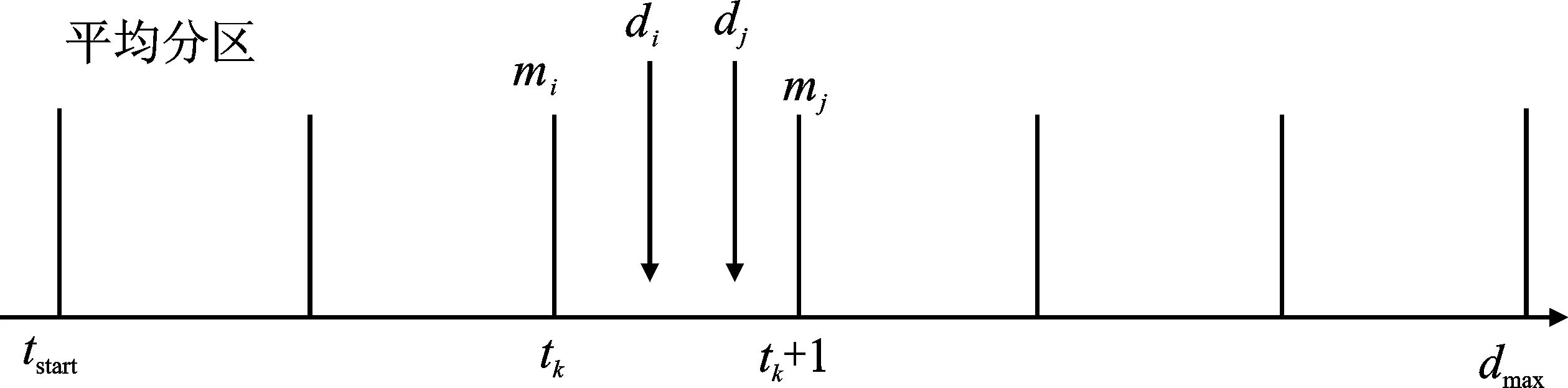
1.2 可调度性判定
2 改进的EDF算法
2.1 指数分区的母区间

2.2 幂函数分区的子区间

2.3 优先级的计算


2.4 误差及可调度性分析
3 实验结果及分析
3.1 模型设计

3.2 仿真实验设计
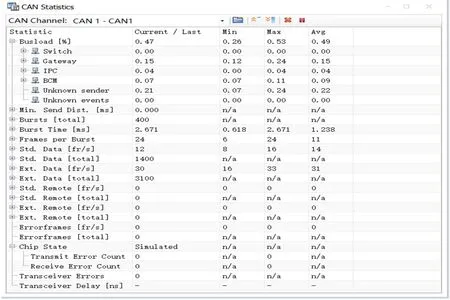
3.3 结果及分析

4 结束语
