基于分时电价和用户侧储能的配电网调度优化策略

王玉梅，王露露

(河南理工大学 电气工程与自动化学院，河南 焦作 454000)

针对分布式电源接入配电网[1-3]及用户负荷波动[4]引起线路损耗增加的问题，通过实施分时电价[5-6]、合理调控分布式储能[7]可改变电网的功率分布，从而降低网损。文献[8]综合考虑了电力需求波动成本、用户对电价变动的负荷响应、用户满意度等多种因素，建立电网公司与用户博弈的分时电价定价模型，有效提高了电网和电力用户双方利益。文献[9]以线路损耗为约束构建了峰谷分时电价模型，达到网损优化的目标。

近年来，随着储能技术的成熟和储能成本的下降，用户侧分布式储能商业化趋势正稳步发展。目前针对用户侧储能的研究多集中于用户侧分布式储能的优化配置问题[10]和用户侧分布式储能系统的规划问题[11]。文献[12～13]以降低配电网电压偏差和网损对分布式储能选址定容优化。文献[14]采用遗传算法研究配电网线损最小的分布式储能充/放电策略。文献[15]采用一种追踪负荷和电价波动的储能充放电策略来平缓负荷波动。文献[16]分析了用户侧分布式储能的运行方式对配电网网损的影响，但未研究具体充放电策略。

随着分布式能源发电容量的扩大及分时电价的广泛应用，用户侧储能容量将同步增长。本文对用户侧储能并网后参与配电网的优化运行进行了研所，所提出的方法可有效降低配电网网损。

1 基于分时电价的负荷转移模型及用户侧储能并网模型

1.1 基于分时电价的负荷转移模型

实施峰谷分时电价后，用户对电价刺激作出响应进行负荷转移，包括峰-谷时段的负荷转移、峰-平时段的负荷转移、平-谷时段的负荷转移3种情况。从高电价时段向低电价时段转移负荷与高电价时段未进行负荷转移前的负荷之比为负荷转移率[17]。峰-谷时段负荷转移率曲线如图1所示。

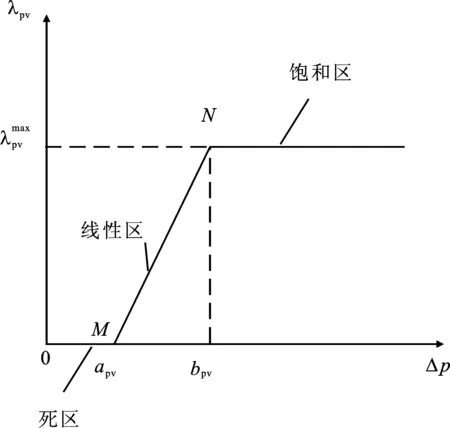
图1 峰-谷时段负荷转移率曲线Figure 1. Peak-to-valley load transfer rate curve

峰-谷时段负荷转移率为

(1)

峰-平时段的负荷转移率和平-谷时段的转移率计算式同式(1)类似。

实行峰谷分时电价后，各时段的负荷值为

(2)

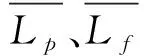
1.2 用户侧储能并网模型

用户侧接入配电网的模型如图2所示。在用户侧储能并网后，整个配电网的潮流流向与分布将发生变化，配电网的网络损耗也将随之变化。

图2 某节点接入用户侧储能的模型图Figure 2. The model diagram of accessing user-side energy storage

当用户侧储能没有接入时，配电网某线路的损耗为

(3)

式中，lloss为节点i、j之间的线路网损；Pj、Qj分别为节点j的有功功率和无功功率；Vj为节点j的电压；Rij+jXij为节点i和j之间线路的阻抗。

当用户侧储能接入配电网后，接入点的线路损耗为

(4)

式中，PjBess、QjBess分别为节点j接入的用户侧储能装置发出的有功功率和无功功率；a和b分别为储能装置发出有功、无功功率的状态；吸收功率为1，发出功率为-1。

2 分时电价下用户侧储能的优化运行模型

考虑用户侧储能参与配电网的优化运行，在降低用户用电成本的同时，通过平滑负荷来降低网损，提高配电网运行经济性。

2.1 目标函数

2.1.1 用户日用电成本函数

用户侧配置储能以用户日用电成本最小为目标函数，成本包括储能安装成本日均摊量、运维成本日均摊量等，储能收益包括“低储高发”套利、政府电价补贴等。具体如式(5)所示

(5)

其中

(6)

(7)

式中，Pk为第k时段电价；Qk为第k时段用户用电需求量；C1为储能设备初始投资成本日均摊量；C2为运行维护成本日均摊量；C3为储能设备回收价值日均摊量；S1为用户侧储能的日套利收益；S2为用户侧储能参与调峰获得的日政府补贴；Pmax为储能装置额定充/放电功率；Emax为储能装置额定容量；T为储能装置寿命；Cp、Ce、Cm分别为储能装置单位充/放电功率成本、储能装置单位容量成本、储能装置单位充/放电功率年运行维护成本；tr为通货膨胀率；dr为贴现率；μ为回收系数，通常取3%～5%；Pch(k)、Pdis(k)为在第k时段储能装置实际的充/放电功率；mk、nk为在第k时段储能装置的充/放电状态；Δtk设置为1 h；Pe为政府补偿电价。

2.1.2 配电网网损函数

用户侧储能的接入可以更好地实现削峰填谷，降低网络损耗。以配电网网损最小的目标函数为

(8)

式中，f2(x)为配网网网损；Pl，loss为支路l的有功损耗；Ql，loss为支路l的无功损耗；NL为支路个数。

2.2 约束条件

本文所建约束条件包含节点电压约束、峰谷电价比约束、储能装置相关约束等。

2.2.1 峰谷电价比约束

1.96≤δ≤5

(9)

式中，δ为峰谷电价比值，通常处于(1.96，5)之间。

2.2.2 配电网潮流平衡约束

(10)

式中，Pcal和Qcal分别为主电网在节点j处注入的有功和无功功率。

2.2.3 功率平衡约束

Pdg+Pgrid=Pload+Ploss+Pess

(11)

式中，Pdg为分布式电源输出有功功率；Pgrid为电网输出有功功率；Pload为系统有功负荷；Ploss为系统有功损耗值；Pess为储能装置输出有功功率，充电为正，放电为负。

2.2.4 节点电压约束

(12)

式中，Vmax、Vmin分别为某节点电压最大值、最小值；δmax、δmin分别为某节点电压相角的最大值、最小值。

2.2.5 分布式电源出力约束

(13)

式中，PDGmax、PDGmin分别为分布式电源有功功率输出最大值、最小值；QDGmax、QDGmin分别为分布式电源无功出力输出最大值、最小值。

2.2.6 储能装置相关约束

(14)

式中，Soc为储能荷电状态；Socmax、Socmin分别为储能荷电状态的上下限；ηc、ηd分别为储能装置充/放电效率。

由于两目标量纲不同，本文利用评价函数法[18]将多个目标优化成单目标问题进行求解。首先，采用规范目标法将量纲不同的目标进行归一化处理；然后求出每个单目标优化的最优值，构造评价函数

(15)

式中，k为目标个数；f、f*分别为第x个单目标的目标值和该目标的最优值。

基于以上方法，本文构造的优化后的单目标函数为

(16)

式中，Pprice为用户用电成本；PL，loss为支路L的线损。

3 遗传模拟退火算法

基于传统遗传算法，本文采用模拟退火算法的Metropolis准则对更新后的个体寻优，改善了传统遗传算法收敛性较差的缺陷。算法流程如下：

步骤1交叉操作。采用遗传算法中的交叉操作，根据每一代计算结果中适应度的高低对所有个体进行排序，适应度较高的一半个体直接进入下一代。根据交叉概率在剩余个体中反复筛选，多交叉；

步骤2采用Metropolis准则筛选交叉后个体。由于变异操作导致更新后的部分个体位置劣于更新前，故需要计算更新后个体的适应度值。设更新前后个体的适应度值为f(x1)、f(x2)、f(x′1)、f(x′2)，通过Metropolis准则进行筛选；

步骤3变异操作。根据变异概率选取一部分个体，利用高斯变异公式对个体进行变异操作。变异计算式为

x′i=xi×(1+Gaussian(σ))

(17)

其中，x′i为xi变异后的位置；Gaussian(σ)服从N(0，1)正态分布；

步骤4Metropolis准则筛选变异后个体。参考交叉操作后的流程。

4 算例分析

IEEE-33节点配电网系统的结构如图3所示。首端基准电压为12.66 kV，各支路阻抗与节点负荷见文献[19]，节点7和15分别接入容量为1 MW的风电、光伏机组。假设2、3、7、8、11、12、17、18、23、24、30节点的负荷参与分时电价，其余不参与。节点30为某10 kV工业用户，其典型日负荷曲线及该地区分时电价曲线如图4所示。根据文献[20]，λpv=0.04，λpf=0.02，λfv=0.01。

图3 IEEE-33节点配电系统结构图Figure 3. Structure diagram of IEEE 33-bus distribution system

图4 负荷曲线和电价曲线Figure 4. Load curve and electricity price curve

为验证本文所提策略的有效性，设置不同场景进行比较分析：

场景1系统不实行分时电价，不考虑用户侧储能的接入；

场景2系统实行分时电价，不考虑用户侧储能的接入；

场景3系统实行分时电价，考虑用户侧储能的接入，采用传统遗传算法对储能充放电策略进行求解；

场景4系统实行分时电价，考虑用户侧储能的接入，采用改进遗传模拟退火算法进行求解。

不同场景下配电网网损变化曲线及用户侧储能充放电策略分别如图5、图6所示，表1为不同场景下用户日用电成本。

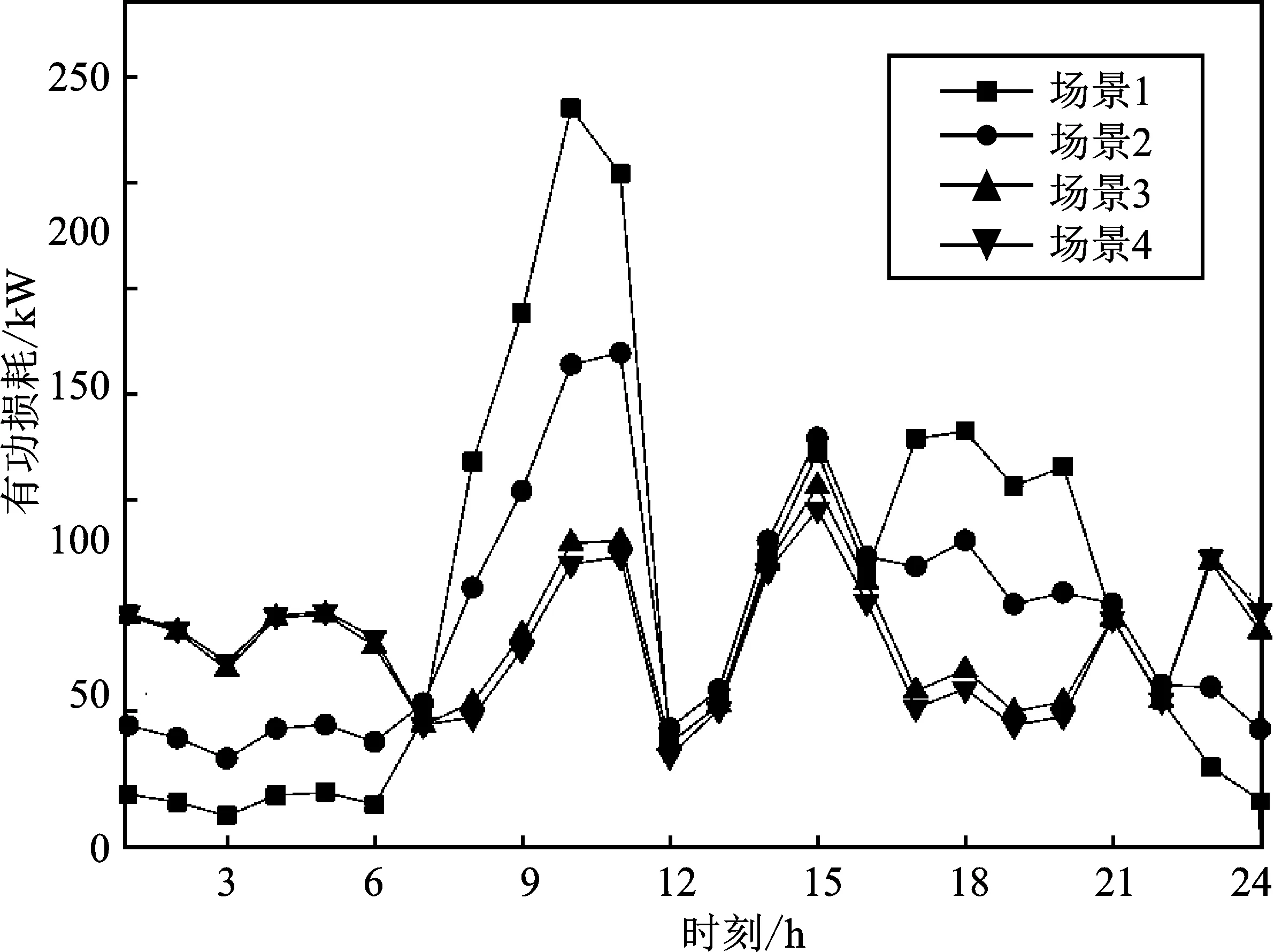
图5 不同场景下配电网网损Figure 5. Load curve and electricity price curve

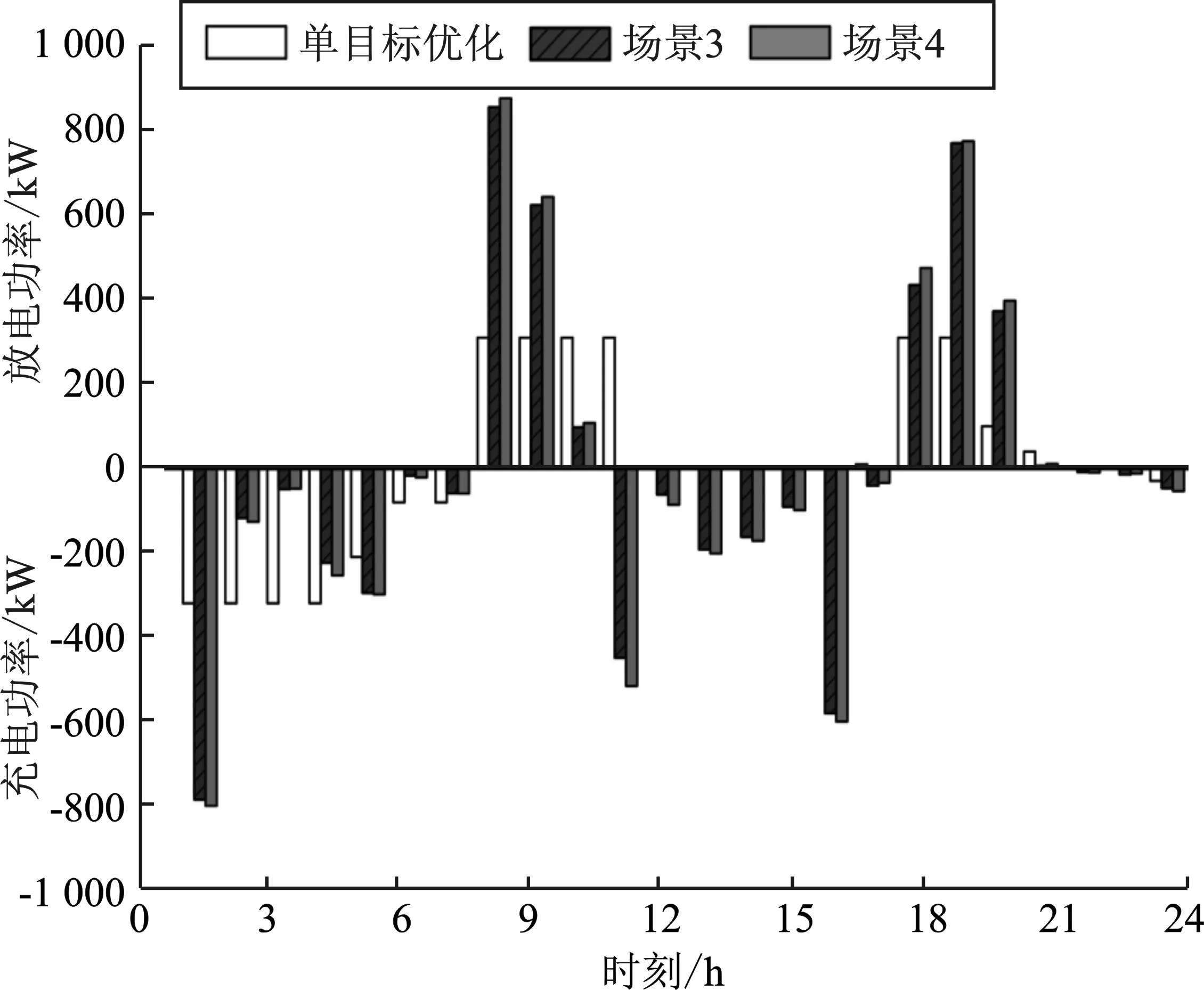
图6 储能充放电策略Figure 6. Energy storage charging and discharging strategy

表1 不同场景下目标函数值

综合图5和表1结果可看出，实行分时电价后，用户主动调整用电方式进行负荷转移可有效降低峰谷差，配电网网损降低了180.44 kW，用户日用电成本降低了7.89%；在用户侧储能接入后，系统在负荷高峰时的损耗有所降低，在负荷低谷时的损耗有所增加，总体上损耗曲线更加平缓；当采用传统遗传算法求解目标函数后，配电网网损降低了347.6 kW，用户日用电成本降低了16.55%；采用改进遗传模拟退火算法求解，用户日用电成本基本一致，配电网网损降低了367.4 kW，相比采用传统遗传算法的求解结果减少了20 kW。

从图6中可看出，当优化目标仅为降低用户用电成本时，用户侧分布式储能仅在低电价时段充电、高电价时段放电以降低用电成本；当优化目标变为多目标时，用户侧分布式储能在0∶00～7∶00、11∶00～16∶00进行充电储能，在8∶00～11∶0、18∶00～20∶00释放电能，即充放电策略由“一充一放”变为“两充两放”，在高电价时段处于充电状态可吸收风电、光伏发出的多余电量，降低网络损耗。

将传统遗传算法与本文提出的遗传模拟退火算法的优化结果进行对比，结果如图7所示。图7中，曲线①和曲线②分别为采用传统遗传算法和遗传模拟退火算法求解的收敛曲线。传统遗传算法约进化到第47代才开始收敛，而采用本文所提算法进化到第14代左右就开始收敛，进化速度快且收敛性能好。

图7 两种算法的迭代结果对比Figure 7. Comparison of iterative results of the two algorithms

5 结束语

本文针对分布式电源接入及负荷的波动引起配电网线路损耗增加的问题，利用用户侧储能主动调整自身负荷需求的特性，将用户侧储能接入以优化配电网的运行，采用改进遗传模拟退火算法优化、求解用户侧储能充放电策略，并基于IEEE-33节点配电系统进行仿真。仿真结果表明，本文所提策略降低了用户用电成本及网络损耗，提高了配电网运行经济性。与传统遗传算法相比，本文所提算法在寻优速度、收敛性能方面均具有一定的优势。