新课标下高中数学课堂教学中数学建模素养渗透方法与策略

孙 峰

(乐山师范学院,数理学院,四川 乐山 614004)

数学是一门研究数量、结构、变化、空间以及信息等概念的学科。数学与人类生活和社会发展紧密相关，在人类历史发展和社会生活中，数学发挥着不可替代的作用，它是各门科学和技术的基础和工具，在自然科学、工程技术、系统科学、管理科学及社会科学等领域起着举足轻重的作用。正如著名数学家华罗庚教授所说：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学。”[1]数学的应用已经渗透到现代社会及人们日常生活的各个方面。然而，作为一门基础的自然学科和一种精确的科学语言，数学又是极为抽象的，它是如何应用于实际问题，并非显而易见。数学如何用，是需要一定的技巧和手段的。数学建模在实际问题与数学之间架设了一座桥梁，是运用数学的语言和方法解决实际问题的一种强有力的数学手段。数学建模不仅能加深学生对数学的理解，还能提高学生学习数学的兴趣。对于中学生而言，不仅要“学数学”，还要“用数学”。《普通高中数学课程标准( 2017 年版2020年修订)》[2]中将数学建模列为高中数学学科六大核心素养之一，足见数学建模的重要性。但是，从高中生数学建模素养调查研究[3-6]发现高中生对数学建模的认知不足，数学建模素养普遍不高，数学建模能力较差。提升高中学生的数学建模素养是必要的。在本文中，我们将探讨高中数学课堂教学中数学建模素养的渗透。

一、数学建模素养及其意义

数学模型是对实际问题的一种数学模拟，是针对具体实际问题，为了特定目的，简化、抽象得到的一个数学结构(包括数学公式、图形或算法等)。数学建模就是建立数学模型解决实际问题的全过程，是运用数学的语言和方法，通过抽象、简化建立能近似刻画实际问题的模型并加以解决的一种数学手段。粗略来说，数学建模可以分成三大部分：实际问题转化为数学问题，数学问题的解决，数学结果返回实际。根据姜启源等的经典著作[7]，数学建模的具体步骤包括：模型准备、模型假设、模型构成、模型求解、模型分析、模型检验和模型应用。数学建模在现实问题与数学之间架设了一座桥梁，其重要性是不言而喻的。《普通高中数学课程标准( 2017 年版2020年修订)》[2]中将数学建模列为高中数学学科六大核心素养之一，并介绍到“数学建模素养是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养。主要表现为：发现和提出问题，建立和求解模型，检验和完善模型，分析和解决问题”。

在高中数学课堂中渗透数学建模素养，提高学生的数学建模能力，具有以下意义：

(1)有助于加深学生对数学的理解，实现从“学数学”到“用数学”的转变。在以往的教育中，学生往往只关注数学理论知识的学习，忽略数学的应用，不清楚数学知识到底有何用，只知道埋头学习。在注重“素质教育”的今天，课堂中渗透数学建模素养后，学生知道数学是如何具体地作用于现实问题，知晓数学有用，并知道如何用。有了数学建模在现实问题实践中的支持，学生对数学理论知识的理解将会更加深刻，并且逐步形成“用数学”的能力。

(2)有助于提高学生学习数学的兴趣。在数学课堂教学中加入一些和实际生活相关的数学建模案例，因为案例贴近生活，不像数学知识那般抽象枯燥，所以这些案例的引入，能充分调动学生的探索欲和求知欲，从而激发并调动学生学习相关数学知识的兴趣。在实际问题的有效解决后，学生更加折服于数学的实用性，对数学的学习兴趣会进一步提高。

(3)有助于学生积累数学实践的经验，提升实践能力。数学建模是学生运用数学知识解决实际问题的实践活动，学生经历一系列的数学建模活动，“学以致用”可得到充分体现，数学实践经验不断累积，实践能力逐步提升。

(4)有助于学生增强创新意识和创新能力。数学建模旨在用数学解决生活中的实际问题。这些问题往往没有现成的解决方法，需要学生根据实际问题做出抽象简化。另外，这些实际问题的解决往往没有统一的标准答案，只要言之有理都是可行的，这鼓励学生提出各种各样的解决办法，包括一些打破常规的想法和思路，这对学生创新意识和创新能力的提高有促进作用。

二、数学建模素养培养现状

数学建模素养写入《普通高中数学课程标准》已经有一段时间，但是相关调研[3-6]发现，高中生的数学建模素养并不高，存在以下问题：

(1)对数学建模的重视程度不够。部分高中生仍处于“应试”模式，以高考为目的，如果高考中对数学建模不作要求，就不会重视数学建模相关案例。

(2)对数学建模的认知水平整体不高。大部分高中生对数学建模的含义、步骤等方面理解不够清晰，对数学建模的知识内容涉及较少，没有表现出对数学建模的兴趣。

(3)缺少数学建模的全过程教学。数学建模教学存在“应用题”化的教学，把数学建模等同于应用题，缺少对实际问题的剖析和提炼，缺少如何把实际问题数学化的过程，没有实现数学建模的全过程教学。

(4)数学建模的实践较少。部分高中生没有参与过数学建模活动，在日常生活中也很少运用数学知识来解决实际问题。

(5)数学建模能力普遍不高。根据《普通高中数学课程标准》中数学建模水平的划分，大部分高中生主要集中在水平一和水平二。大多数学生只能在熟悉情境中利用已经学过的数学模型解决问题，对于适当修改模型以解决类似问题方面的能力稍有欠缺。

三、高中数学课堂中渗透数学建模素养示例

《普通高中数学课程标准》中将课程内容分为“函数”“几何与代数”和“概率与统计”等主题。数学建模素养应在各个主题中得到培养和提升。在日常的教学中渗透数学建模素养，在相关数学知识学习完后讲解相应的数学建模案例，加深学生对知识的理解，让学生掌握数学知识的运用。下面我们将介绍数学建模素养在一些数学专题中的渗透示例。

(一)函数专题中的建模示例

案例1 商铺租金问题——某商铺租金一年2万元，房东为鼓励租客提前交付租金，承诺提前交付的租金可按照银行一年期存款利率予以抵扣。租客欲租10年，并提前一次性交付租金，那么租金多少？

模型分析：提前交付的租金按照一年期存款利率采取复利方式计算，提前交付的租金连同其利息收入抵扣当年租金。

模型假设：租金每年2万元维持不变；存款利率不变，按照当前一年期利率(2%)计算；租户一次性交付10年租金。

模型建立：设S为一次性交付的租金，xi为第i年提前交付的租金，第i年的租金提前了i-1年交付，本息和为xi(1+2%)i-1，因提前交付租金本息和抵扣该年租金，故

xi(1+0.02)i-1=2，

从而

由此可知，一次性交付的租金为

结果解释：租户一次性交付10年租金的话，只需要交18.32万元。

注意，教师在讲解等比数列求和的相关知识后，可介绍该案例。教师在讲解时，应以学生为主，引导学生分析。在计算利息时，我们采取的是复利计算，当然也可以采取单利计算的方式。另外，学生在分析时可能会有这样的思路：租户按每年2万元提前交付租金，房东将提前交付租金产生的利息补偿给客户，以2年租期为例，提前交付租金共计4万元，有2万元提前一年交付，产生的利息为0.04万元，退还后，租户实际交付租金为3.96万元，但按照上述模型计算，交付租金大于3.96万元。教师要引导学生发现问题，这种计算方式的漏洞主要在于利息本应到期后才获得，提前支付不会有那么多。对于学生的不同思路，教师要积极肯定，鼓励并引导学生找出新的解决方法。

案例2 客房的定价问题——某宾馆有客房200间，营业一段时间后，经理得到客房定价和住房率的大致信息：定价280元/间，住房率约50%；定价240元/间，住房率约60%；定价200元/间，住房率约70%；定价160元/间，住房率约80%。欲使宾馆每天获得最高收入，每间客房应定价多少？

模型分析：从所给数据信息看，房间定价每降低40元，入住率增加约10%，由此假设出定价和入住率的关系，进而根据收入最高，确定客房定价。

模型假设：随着客房定价的下降，住房率呈线性增长，即定价下降40元，入住率提高10%；房间定价最高480元(按照第一条假设，480元定价时，入住率为0)；每一间房间的定价相等。

模型建立：设住房总收入为y元，房间定价为x元/间，根据假设相应的入住率为

入住的房间数为

住房收入总收入为

y=0.5x(480-x),0≤x≤480。

模型求解：根据一元二次函数的最值，求解得到x=240,y=28 800。

结果解释：住房定价为240元/间时，住房收入可取得最大值28 800元。

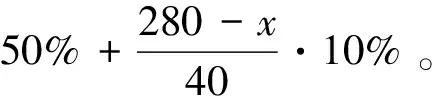
(二)几何与代数专题中的建模示例

案例3 包汤圆问题——同等重量的汤圆粉，包大汤圆和包小汤圆，哪种用馅儿更多？

模型分析：汤圆可以近似看成球体，由汤圆粉做成的外皮和中间的馅儿组成。同等重量的汤圆粉加工得到的汤圆外皮重量是一样的，如果大小汤圆的表皮厚度一样，则大小汤圆外表皮的面积是一样的。因此问题主要在于对比表皮面积相同的大小汤圆的总体积。

模型假设：假设大小汤圆的外皮厚度一样；包汤圆时不对表皮拉扯，保证外皮厚度不变；大小汤圆的规格一致，所有大汤圆都是一样的，所有小汤圆都是一样的；大小汤圆近似看成球体，汤圆馅填充满汤圆内部；汤圆馅大皮薄，忽略表皮的厚度。

模型建立：假设一个大汤圆的表面积S，体积为V，半径为R，共有N个大汤圆；一个小汤圆的表面积s，体积为v，半径为r，共有n(n>N)个小汤圆。汤圆近似看成球体，可得到大小汤圆的表面积和体积为

因大小汤圆外皮厚度一样，故大汤圆和小汤圆总的表面积一样，即ns=NS。从而有

n·4πr2=N·4πR2，

于是可知大小汤圆的半径满足

进一步，大汤圆与小汤圆总体积比为

结果解释：同样重量的汤圆粉，包大汤圆的个数N必然小于小汤圆的个数n，因此小汤圆用的馅儿会更多。若这些汤圆粉可包成大汤圆50个，小汤圆100个，也即是说一张大的汤圆皮可变为厚度相同的两张小汤圆皮，则小汤圆用馅儿的总量将大约是大汤圆用馅儿总量的1.4倍左右。

注意，教师在讲解球的表面积和体积的相关知识后，可介绍该案例。注意引导学生分大小汤圆两组对比考虑。另外，模型相对粗糙，在计算时，忽略了汤圆表皮的厚度。

(三)概率与统计专题中的建模示例

案例4 掷骰子游戏问题——某公园有一个掷骰子的“有奖游戏”摊位，玩家2元可掷骰子一次，若两骰子点数之和为7，则获得奖励5元，否则无奖励。试问该游戏对玩家公平吗？

模型分析：需要计算出玩家的期望收益，如果为0，说明玩很多次，将会不输不赢，游戏是公平的；如果小于0，说明对玩家不公平。

模型假设：骰子没有任何问题，掷出点数1到6的概率都是均等的；游戏规则有效。

模型建立：两骰子点数之和可为2到12之间的任何自然数，表1中给出了具体的情况。

表1 两骰子点数之和

模型求解：玩家的期望收益为负，约为-0.83。

结果解释：游戏对玩家是不公平的，如果玩100次，玩家就会输掉大约83元。

注意，教师在讲解概率及期望的相关知识后，可讲解该案例。教师需要说明期望的含义。另外，教师还可以对案例进行拓展，让学生考虑，公平的游戏，玩一次的费用或者奖励金额应该如何调整。此外，还可以考虑中奖号码为多个，奖励金额不同的情况。

四、高中数学建模的教学建议

数学建模对高中生数学学科素养的提升和数学应用能力的发展是至关重要的。然而，数学建模素养的提升并非一朝一夕就可以实现，是循序渐进的。笔者建议教师在进行数学建模教学活动时注意以下几点：

(1)集中讲解与分散渗透结合。《普通高中数学课程标准》中建议“数学建模活动与数学探究活动”必修课程课时6学时，选择性必修课程课时4学时。如果对“数学建模”专题集中讲解，学生虽然对建模会产生一定的强化认识，但难免会忽略数学建模与其他主题相关知识的关联。因此，笔者建议，在进行数学建模相关的教学活动时，既要有集中的时段进行专题讲解，系统介绍数学建模的含义及步骤等相关知识，也要分散到各个教学主题中，在相关数学知识讲解后介绍相应的建模案例，在日常教学中渗透数学建模素养。

(2)合理选题。数学建模的教学案例最好来自于学生的生活实际，是学生生活或学习中的现实问题，这样的问题能有效调动学生的探索欲和求知欲。另外，案例不能过于复杂，是能够解决的，涉及的数学知识应是学生已经学习并掌握的内容。如果案例过于复杂，学生无法接受，并不利于数学建模的开展。

(3)展现数学建模的全过程。数学建模与一般意义的应用题是不一样的，应用题侧重解决问题，而数学建模包括问题转化及问题的解决等。数学建模素养是系统的，包括提出问题、分析问题、解决问题等。教师要按照数学建模的大致步骤操作，引导学生分析问题，详尽展示生活实际是如何通过简化抽象转化为数学问题的，并将模型求解的结果返回生活实际。对于一些案例，进行必要的检验、参数分析、改进和拓展迁移等。让学生在数学建模的全过程中提升素养。