基于改进CNN的轴承声学故障诊断

黄雅静，廖爱华，于 淼，李晓龙，胡定玉，3

(1.上海工程技术大学 城市轨道交通学院，上海 201620； 2.中国铁路哈尔滨局集团有限公司 哈尔滨动车段，黑龙江 哈尔滨 150000； 3.上海市轨道交通振动与噪声控制技术工程研究中心，上海 201620)

目前，我国轨道交通行业处于迅猛发展阶段，在便利出行、促进经济发展的同时，保证车辆行车安全成为社会高度关注的话题。滚动轴承作为轨道车辆的关键部件之一，承担着传动和承载的多种功能，其健康状态直接影响轨道车辆的安全运行。由于行车环境复杂，在多种因素的共同作用下，轴承容易发生疲劳损坏等多种故障[1]。列车滚动轴承故障会降低乘客乘坐舒适性，甚至造成不可估量的事故。因此，对滚动轴承进行状态监测和早期故障诊断非常重要。

随着工业智能化、轨道智慧化的发展，智能故障诊断技术被广泛应用于旋转机械故障诊断中[2]。传统的智能故障诊断使用小波变换[3]、经验模态分解[4]等信号处理方法提取信号特征，然后使用支持向量机(Support Vector Machine，SVM)[5]、多层感知机(Multilayer Perceptron，MLP)[6]等机器学习模型判别健康状态。然而，这需要大量的前期研究和专业知识，且模型的学习能力相对较差。近年来，随着人工智能的不断发展，深度学习为机械故障诊断提供了全新的解决方法[7]。卷积神经网络作为深度学习的模型之一，已经被成功运用于轴承智能故障诊断中。文献[8]提出了一种带训练干扰的卷积神经网络(Convolution Neural Networks with Training Interference，TICNN)用于轴承故障诊断，通过改变轴承运行的噪声环境和工作负载证明模型的强鲁棒性。文献[9]提出了一种基于特征通道权重调整的卷积神经网络(Squeeze-Excitation Convolutional Neural Network，SECNN)轴承故障诊断方法，将特征通道调整模块与卷积模块结合。该模型在多个变负载工况下依然保持强诊断性能。文献[10]将卷积神经网络和双向长短记忆神经网络结合构建WConv-LSTM(Wide Convolution-Bidirectional Long and Short Memory)模型，并证明WConv-LSTM能够提高不同信噪比下轴承故障诊断精度。

常见的轴承故障诊断方法均基于轴承振动信号，振动信号容易获取且包含丰富的设备状态信息。然而，振动加速的安装位置直接影响测得信号的质量。在复杂的机械设备中，振动加速传感器的安装受限，无法达到理想的测量效果[11]。声学信号采用非接触式测量方法进行测量，在更加方便快捷的同时也包含了机械丰富的运行信息。文献[12]提出了一种基于声信号的行星齿轮箱故障诊断方法，将傅里叶分解方法和随机森林模型结合，在实验条件下取得了比振动信号更好的故障诊断效果。文献[13]将图卷积神经网络用于轴承声学故障诊断，且实验结果表明模型的诊断性能优于传统的深度学习方法。

在实际工业环境中，机械背景噪声大，轴承信号的故障信息容易被淹没。为增强轴承的冲击特性，提高模型的诊断性能，本文结合卷积神经网络和Teager能量算子，提出一种基于Teager 能量算子和卷积神经网络的卷积故障诊断模型(Teager Energy Operator and Convolution Neural Network，TEO-CNN)。Teager能量算子能够快速准确地追踪信号的瞬时变化，适合于冲击信号特征的提取[14]。本文提出的方法首先通过Teager能量算子对信号进行增强，然后使用基于卷积的模型学习信号深度特征和诊断轴承类型。

1 基本理论

1.1 Teager能量算子

Teager能量算子是一种非线性差分算子，用于估计信号在时域中的瞬时能量。它对信号的瞬时变化有较好的分辨率，可以突出信号的冲击特性，被认为是一种高分辨率的能量估计器[15-16]。连续信号x(t)的Teager能量算子计算如下

(1)

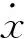
Ψ[xn)]=x2n)-xn+1)xn-1)

(2)

根据式(2)，仅需要3个样本数据就能够计算某时刻的能量值，计算简单，对网络训练速度影响较小。

1.2 一维卷积神经网络

卷积神经网络(Convolutional Neural Network，CNN)是一种多层有监督前馈神经网络，旨在通过交替堆叠卷积核和池运算来学习输入的抽象特征。CNN具有权值共享和稀疏连接的特点，一般由卷积层、池化层、全连接层构成。本文重点讨论一维卷积神经网络，模型结构如图1所示。

1.2.1 卷积层

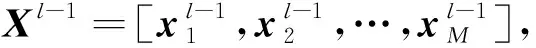
(3)

(4)

1.2.2 池化层

池化层是一种下采样方法，通过滑动窗口对卷积后的特征降维，减少网络参数。常见的池化操作包括最大池化、平均池化等，以最大池化为例，池化过程如下

(5)

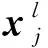
1.2.3 全连接层

在堆叠多个卷积、池化模块之后，通常使用全连接层来进一步处理特征。全连接层由多个神经元构成，数学计算与传统感知机相同。假设第l层全连接层输出特征为fl=[f1，f2，…fn]，第l+1层的计算过程为

fl+1=σwl+1fl+bl)

(6)

式中，wl+1和bl分别为第l+1层的权重和偏置偏置；σ(·)为激活函数。

2 TEO-CNN故障诊断方法

2.1 模型结构

为了增强故障信息的冲击特性，提高模型的诊断性能，本文在传统的卷积神经网络中加入Teager能量算子层，构成一个新的故障诊断模型，简称为TEO-CNN。

模型结构如图1所示，TEO-CNN共包含3个卷积模块和1个全连接层。首先，轴承声信号输入Teager能量算子层计算信号的Teager能量值，增强信号的冲击特征；然后，卷积层对信号的Teager能量值进行特征提取，并且通过ReLU激活函数非线性转化特征；最后采用最大池化层对卷积后的特征降维，过滤出重要的特征信息。信号经过3次卷积和池化，获得了最后的深度特征。值得注意的是，在全连接层前，模型加入了全局平局池化(Global Average Pooling，GAP)层，GAP通过学习空间信息进一步对特征降维。最终的抽象特征被输入到全连接层中，并使用Softmax分类器区分轴承的健康状态。

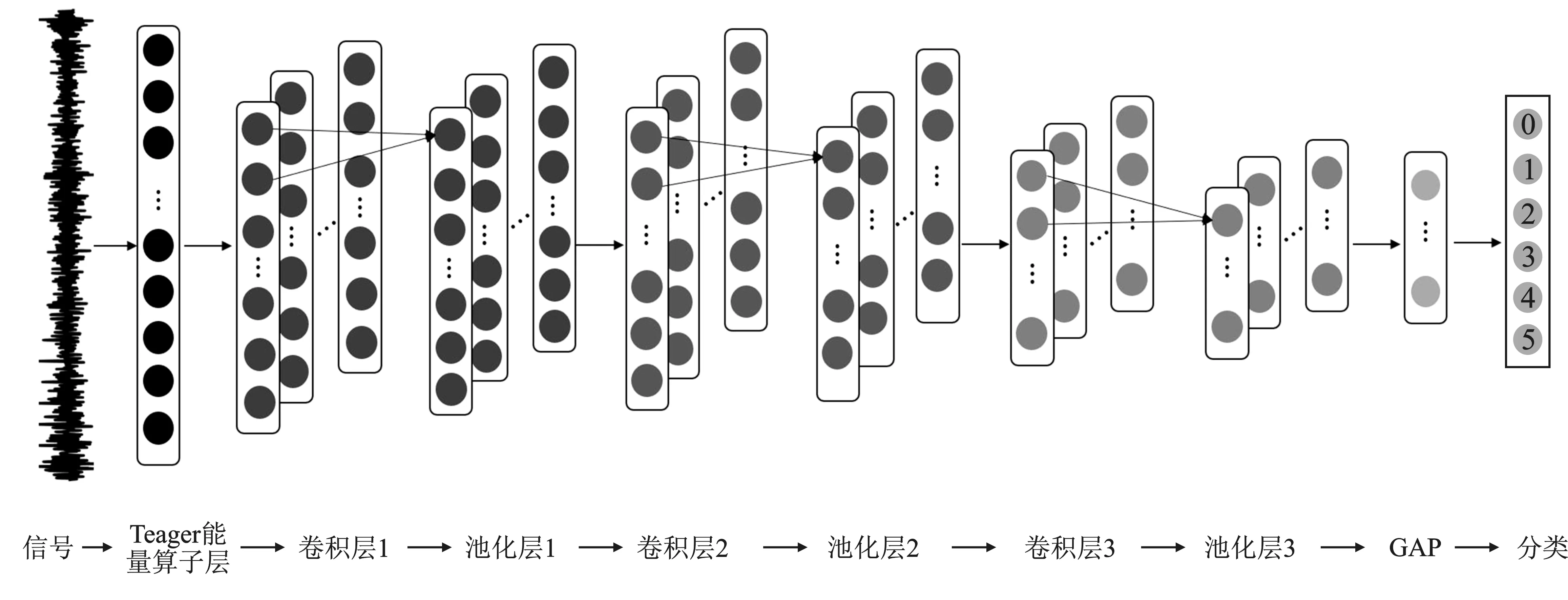
图1 TEO-CNN模型框架Figure 1. The framework of the proposed TEO-CNN model

TEO-CNN的参数设定见表1。其中，第1层卷积层使用宽核，能够进一步降低高频噪声，后两层卷积核逐渐减小，层数逐渐增多，有利于进一步提取信号的抽象特征。在TEO-CNN模型的训练过程中，选择Adam优化器，学习率为0.002，损失函数为交叉熵函数，批量大小为60，共训练60次。

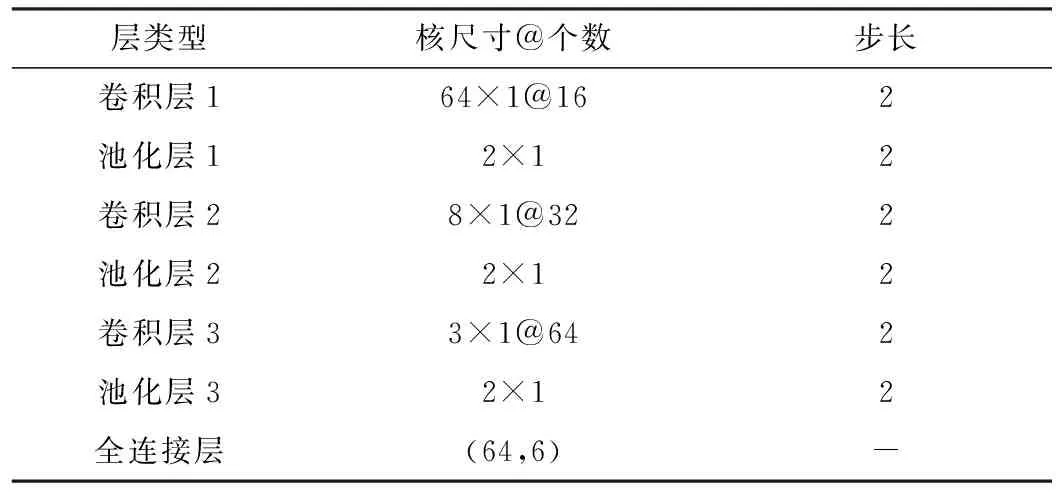
表1 TEO-CNN模型参数Table 1. The parameters of TEO-CNN

2.2 模型诊断流程

基于TEO-CNN模型的故障诊断流程如图2所示，诊断步骤如下：

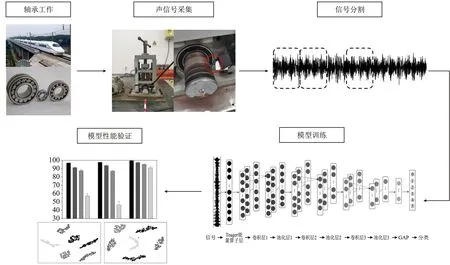
图2 基于TEO-CNN模型的轴承诊断流程图Figure 2. The flow chart of bearing diagnosis based on TEO-CNN model

步骤1采集不同工况下、不同故障类型的轴承声信号，以2 400个点为一个样本将采集到的信号分段并打上类别标签，按照3∶1的比例随机选择样本构建训练集和测试集；

步骤2初始化网络模型参数，使用训练集训练TEO-CNN模型，然后损失函数通过反向传播算法调节模型参数，反复迭代直至模型收敛，结束训练并保存模型；

步骤3将测试集输入训练好的模型中，预测轴承类别，并通过与已知类比标签比较，计算预测精度证明模型的有效性。

3 实验与分析

3.1 实验数据描述

本次模型验证利用图3所示的轴承试验台采集轴承声学信号。测试的滚珠轴承型号为SKF6016，共测试6种健康状态的轴承，分别为正常轴承、内圈、外圈、滚动体故障轴承和两个混合故障轴承，混合故障分别为内圈+滚动体、外圈+滚动体。声学传感器为1/4传感器，放置在测试轴承附近，详见图2，采集两种不同转速工况下轴承声学信号，采样频率为12 kHz。声学信号采集过程中，每次采集时长为30 s，每次间隔时长为1 min，共采集5次。为保持数据一致性，5次采集过程中实验台未停止运转。

图3 轴承实验台Figure 3. The bearing test rig

不同转速下，每个样本包含2 400个数据点，信号均匀分段后，每个轴承共有800个样本。为了避免特殊性和偶然性，随机选择600个样本用于训练，其余200个用于测试。表2详细描述了不同工况下的轴承数据集，其中转速1 Hz=57.6 rad·min-1。不同健康状态的轴承时域信号见图4。

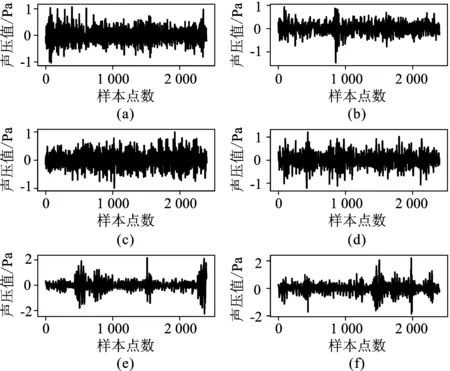
图4 轴承时域信号(a)正常 (b)内圈故障 (c)滚珠故障 (d)外圈故障 (c)内圈+滚珠故障 (f)外圈+滚珠故障Figure 4. Bearing signals in time domain(a)Normal (b)Inner fault (c)Roller fault (d)Outer fault (e)Inner & roller fault (f)Outer & roller fault

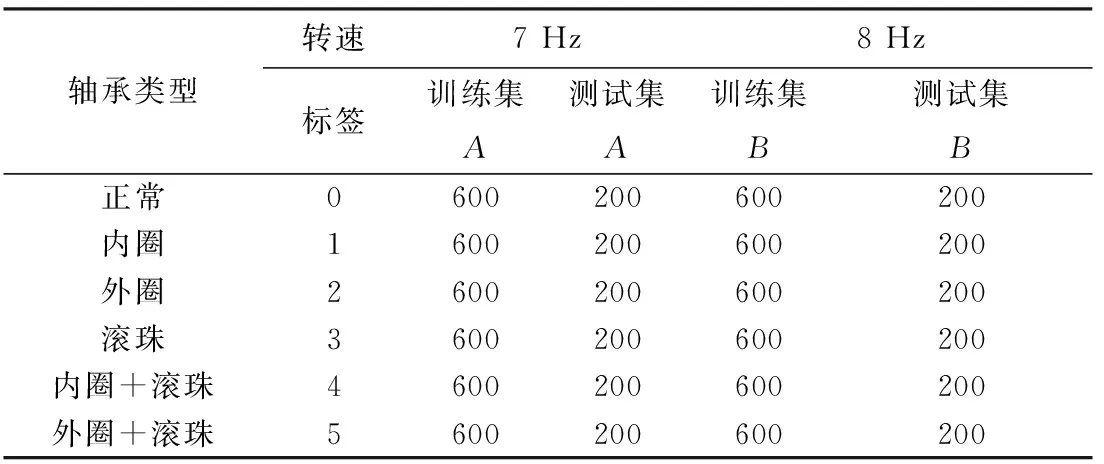
表2 轴承数据集Table 2. The description of bearing data sets

3.2 TEO-CNN模型性能验证

3.2.1 稳态工况下性能验证

首先，以数据集A为例训练和测试模型TEO-CNN的性能。模型的学习曲线和混淆矩阵如图5、图6所示。整个学习过程中，模型在20次迭代后达到100%的预测精度，未出现过拟现象，具有强诊断性能。

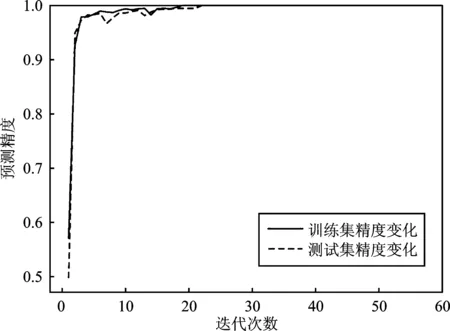
图5 TEO-CNN的学习曲线Figure 5. The learning curve of TEO-CNN

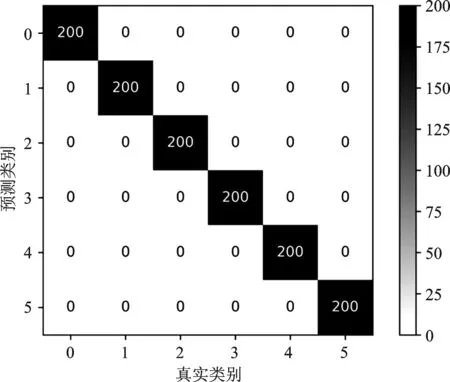
图6 测试集混淆矩阵Figure 6. The confusion matrix of test data set

本节在稳态环境下将模型与传统CNN、MLP和SVM对比，验证TEO-CNN模型的优越性。其中，传统CNN为不加Teager能量算子层和全局池化层的卷积模型，模型参数设置与TEO-CNN相同。MLP由4个全连接层连接，神经元个数为2 400、1 024、512、64、6。为避免模型过拟合，在前两层均加入随机丢弃率为0.5的dropout层。SVM模型的构建参考文献[17]，先提取轴承声信号的时域特征和小波包频带能量特征，再使用SVM对特征分类。稳态条件下模型的预测精度如表3所示。

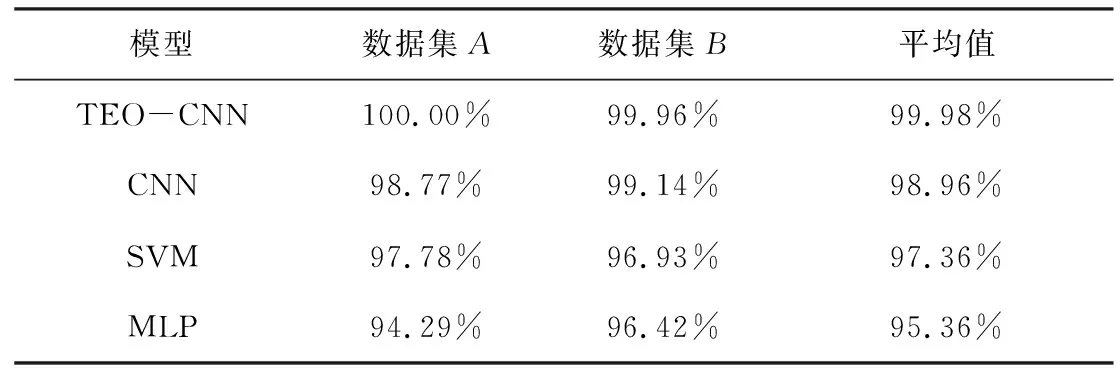
表3 模型预测精度对比Table 3. The comparation of model prediction accuracy

由表3的预测精度对比可以看出，基于卷积模型的诊断性能明显优于MLP和SVM。比较TEO-CNN和传统CNN，Teager能量算子层的加入，使模型学习到更加丰富的冲击信息，增强了模型的诊断性能。经验证TEO-CNN具有强性能表现，在声学诊断中具有明显优势。

为进一步验证TEO-CNN模型的优越性，使用t-SEN[18]方法可视化卷积后的特征。不同转速下，TEO-CNN和传统CNN的特征分布如图7所示。由图7可以看出，经TEO-CNN模型的特征使得信号完全可分，与传统CNN相比具有强特征学习能力。

图7 特征分布可视化(a)7 Hz转速下TEO-CNN特征(b)8 Hz转速下TEO-CNN特征(c)7 Hz转速下CNN特征 (d)8 Hz转速下CNN特征Figure 7. The visualization of feature distribution(a)Features of TEO-CNN at 7 Hz(b)Features of TEO-CNN at 8 Hz(c)Features of CNN at 7 Hz(d)Features of CNN at 8 Hz

3.2.2 跨转速域工况下性能验证

在实际工业环境中，轴承通常处于非平稳运行工况，转速会由于机械设备及生产需要而随之改变。本节主要验证TEO-CNN在跨转速域的非平稳工况下的模型性能。

本节共模拟3种跨转速域工况，数据集见表4。数据集A→B、B→A均模拟轴承诊断跨转速域工况。数据集A&B模拟轴承诊断非稳态混合转速工况。模型的参数均与章节3.2.1相同。本文中，4种模型在3种工况下训练10次的精度变化见表5和图8。

表4 非稳态工况数据集Table 4. The description of bearing data set across speed domains

表5中，当数据集为A&B时，由于模型可以学习到两种工况下的信号，4种模型具有较高预测精度。然而，当数据集中只含有1种工况信号时，模型的预测精度出现明显不同的变化趋势。MLP模型的预测精度低于50%说明已经明显失效，而SVM和传统CNN也存在明显下降，只有TEO-CNN模型具有强泛化性能，预测精度始终高于95%。由图8可知在10次预测精度变化中，TEO-CNN模型的偏差最小。

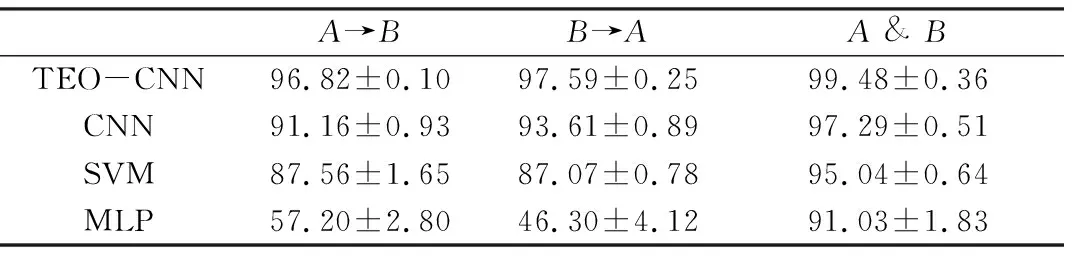
表5 非稳态工况下模型预测精度比较Table 5. Comparation of model prediction accuracy across speed domains

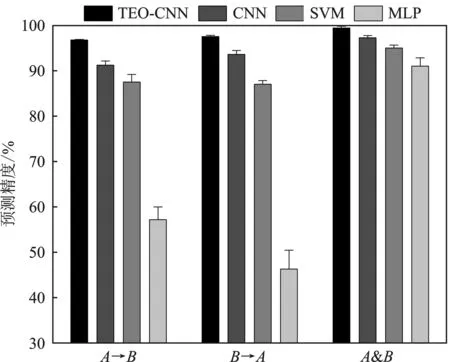
图8 非稳态工况下模型预测精度变化Figure 8. The description of model prediction accuracy changes across speed domains

4 结束语

本文提出了一种基于Teager能量算子和卷积神经网络(TEO-CNN)的滚动轴承声学故障诊断方法。通过实验分析可以得到以下结论：(1)基于声学信号的故障诊断技术可以为滚动轴承的状态监测提供新的解决方法；(2)抽象特征分布可视化证明，Teager能量算子层的加入能够增强模型输入的有用信息，降低整个模型的学习难度；(3)不同工况下，TEO-CNN的预测精度始终高于传统CNN及浅层模型MLP、SVM，表明TEO-CNN模型具有优越的诊断性能和强鲁棒性。