分布式异构集群系统PI编队跟踪控制

唐 凯，章 伟，王为科，胡 陟

(上海工程技术大学 机械与汽车工程学院，上海 201620)

近年来，网络系统的协同控制问题，例如协同攻击、防御以及分布式传感器网络等得到了广泛的研究[1]。继文献[2]首次提出一致性的概念之后，一致性理论，例如抽样数据一致性、有限时间一致性、时延一致性[3]等便受到了各研究领域学者的关注。但早期研究的关注热点为同构集群系统的一致性问题，即集群系统中的智能体有着相同的动力学模型。但是，由于智能体的动态特性或状态空间维度很可能是不同的，因此研究异构集群系统的一致性问题更具实际意义。为了解决带有外部扰动的异构线性集群系统的一致性问题，文献[4]提出了一种分布式PI控制协议。文献[5]在切换拓扑结构下，使用PI控制策略研究了线性异构集群系统的一致性控制问题。但是，文献[4]和文献[5]中的通信拓扑都是无向的。由于在有向图中拉普拉斯矩阵是不对称的，所以在有向拓扑结构下实现异构集群系统的一致性问题较为困难。基于一致性理论的编队控制的核心思想是：多智能体的状态或其输出状态需要与多智能体系统的参考中心保持一定的编队补偿[6]。传统的编队控制主要有基于虚拟结构的编队控制策略[7]、基于有领导者的编队控制策略[8]、基于行为的编队控制策略[9]等。其中，基于有领导者的编队控制方法逐渐成为了重点研究方向。引入领导者可以使跟随者的拉普拉斯矩阵的子阵不具有零特征值[10]，这将有助于解决在有向图下异构集群系统的静态一致性问题[11]。考虑到真实系统往往会受到外部未知扰动的影响，因此研究系统的鲁棒性问题具有实际意义[12]。对此，文献[13]研究了具有外部扰动的不确定二阶非线性系统的分布式时变编队控制问题；文献[14]研究了含有未知参数的异构非线性多智能体系统的编队跟踪控制问题。

基于以上研究，本文的创新之处主要有以下3个方面：(1)通过引入虚拟领导者来保证跟随者跟踪领导者的状态，从而达到期望的空间位置；(2)在有向拓扑结构下设计了一种PI控制策略，研究了在跟随过程中多智能体的编队跟踪控制问题；(3)考虑到实际情况中存在的外部未知有界扰动问题，本文给出了系统形成期望编队队形的充分条件，并给出了编队误差的收敛范围。

1 预备知识和问题描述

1.1 图论知识

引理1[15]对于任意非零矩阵P∈RN×n、对称半正定矩阵M∈Rn×n及对称矩阵L∈RN×N，以下不等式成立。

(1)

引理2[16]在图G0中，包含1簇有向生成树的拉普拉斯矩阵L的特征值都在右半平面内，且至少包含一个以1N作为它的右特征向量的零特征值。

引理3[17]对于任意向量p，q∈Rn，总存在具有合适维度的矩阵向量k∈RN×N，使得下式成立

±2pq≤pTkp+qTk-1q

(2)

引理4[18]对于非奇异矩阵M，存在一个对角正定矩阵H，使得HM+MTH是正定的。

(3)

1.2 问题描述

考虑1组由N个智能体构成的异构集群系统，第i个智能体的动力学模型可以描述为

(4)

式中，xi∈Rn为第i个智能体的状态；ui∈Rn为控制输入；wi∈Rn表示第i个智能体受到的时变外部扰动；Ai∈Rn×n为系统矩阵。

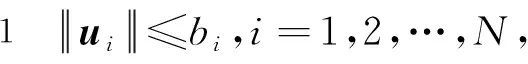
为得到预定的期望值，引入虚拟领导者，其动力学模型为式(5)。

(5)

假设2矩阵A0是Hurwitz的，h0为常数向量。

注释1根据假设2，虚拟领导者的状态x0将会渐近趋于预定的期望值h0。假设2中的条件A0是Hurwitz的，即智能体的系统矩阵是稳定的。不同于文献[4]和文献[5]，尽管h0为常数向量，但它在获得预定的期望值方面起着根本作用。

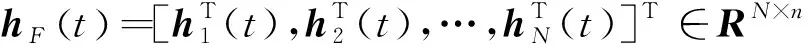
定义1对于异构集群系统式(4)、式(5)而言，若满足

(6)

则称集群系统将会形成期望的时变编队。其中，xit)∈Rn为第i个智能体的状态，初始值有界；hit)∈Rn为第i个智能体的期望时变编队补偿向量；x0t)∈Rn为虚拟领导者的状态，初始值有界。

2 主分布式PI控制协议设计

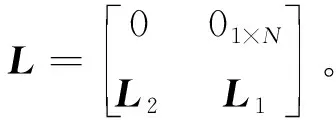
hi(τ))-(xj(τ)-hj(τ))]dτ+ηi(t)

(7)

式中，σI和σP是待设定的正常数；uit)∈Rn，i∈F为第i个智能体的控制输入；hi(t)∈hF(t)为第i个智能体的时变编队控制向量；ηi(t)∈Rn为编队控制补偿项。定义系统的局部一致性误差向量为

ξ=(L1⊗In)(x-h-1⊗x0)

(8)

(9)

结合式(4)～式(9)，系统的闭环一致性误差动态方程可以写为

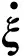
σP(L1⊗In))ξ+y+(L1⊗In)w+

(10)

(11)

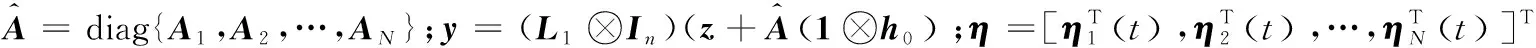
3 鲁棒性分析

由于式(4)中存在外部未知扰动，一致性误差ξ将不再收敛于零，因此需验证式(7)是否具有鲁棒性，以确保一致性误差的有界性。

定理1在假设1～假设3成立的条件下，考虑由N+1个智能体组成的领导者-跟随者异构集群系统，系统动力学模型满足式(4)和式(5)。若满足以下条件

(1)σI>0；

(2)

(12)

证明选取Lyapunov函数

(13)

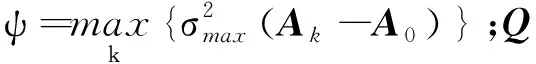
(14)

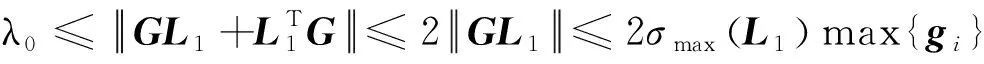
将V(t)对时间求导并将式(11)代入可得

σPξT[(GL1+L1G)⊗In]ξ+

2ξT(G⊗In)y+2ξT(GL1⊗In)w+

σPyT(GL1⊗In)ξ+σIξT(GL1⊗In)ξ-

σPyT(GL1⊗In)ξ-yT(G⊗In)y-

(15)

由矩阵范数的性质，可得

(16)

σIξT(GL1⊗In)ξ≤σIσmax(L1)max{gi}ξTξ

(17)

由引理1可得

(18)

由引理2可得

(19)

(20)

(21)

(22)

(23)

(24)

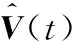
(25)

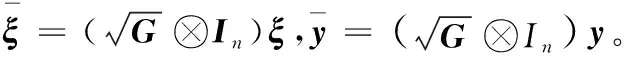
(26)

结合引理1，可得

(27)

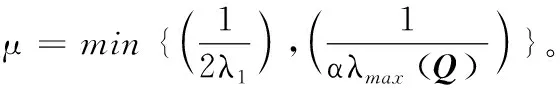
4 数值模拟

使用编号0代表领导者，使用编号1、2、3、4、5分别代表5个跟随者，集群系统的拓扑结构如图1所示。

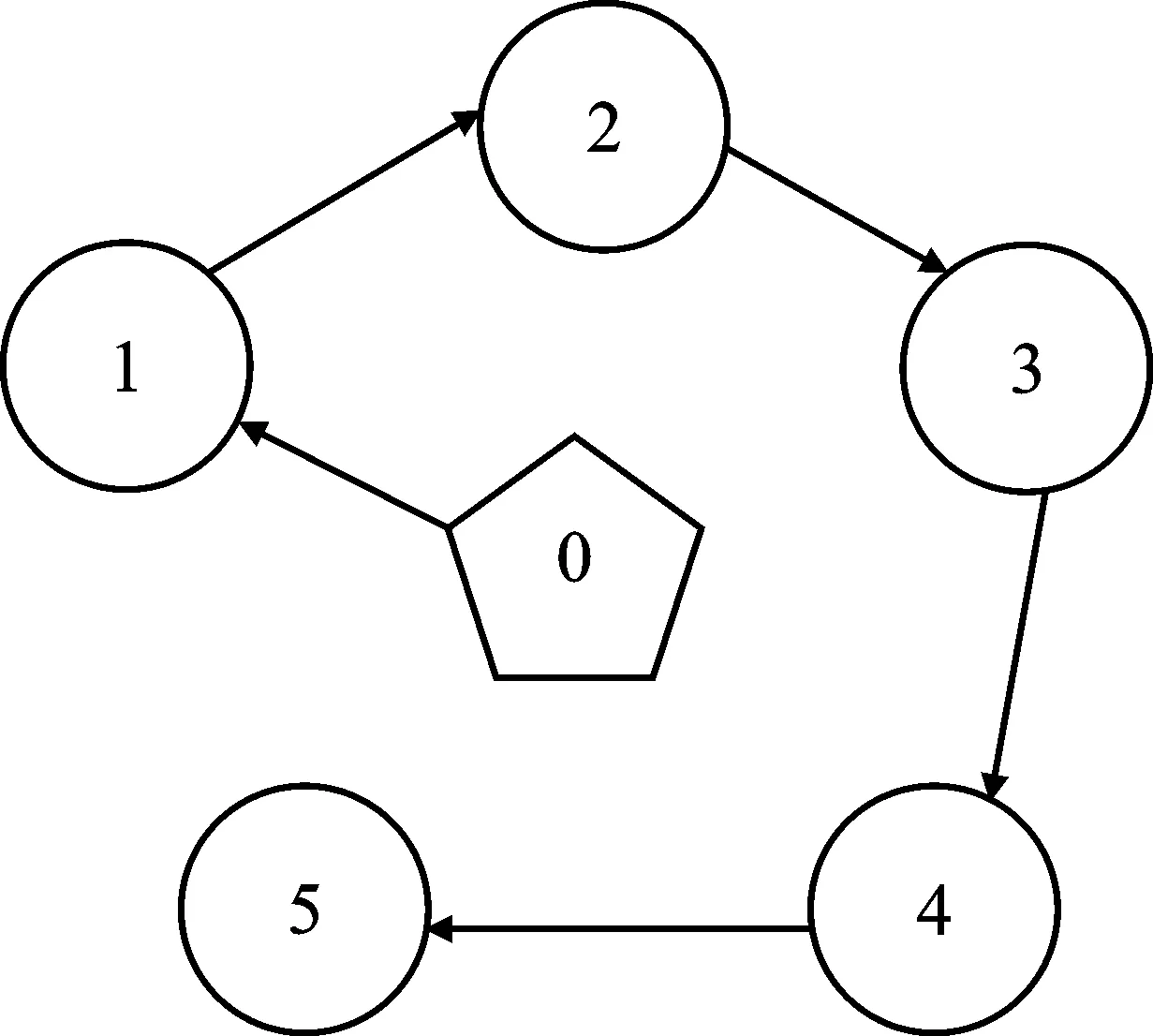
图1 集群系统拓扑结构Figure 1. The topology of swarm systems

由图1可知，系统的通信拓扑结构是有向的，领导者仅与跟随者1通信，拓扑结构中存在一簇有向生成树。考虑实际情况中存在外部扰动等不确定性因素，选择外界扰动函数为wi=0.3sinit)+0.2cosit)，i=1，2，3，4，5，本文使用分布式控制协议在100 s时间内仿真，系统的状态误差变化如图2所示。

图2 误差变化Figure 2. Error change

由图2可以看出，在开始时，由于系统初始状态是随机的，因此系统状态误差较大；随时间增加，误差在控制协议下迅速减小，最后收敛到有界范围。这意味着虽然存在一定的跟踪误差，但是跟随者仍可以有效地收敛到其期望值附近。在收敛过程中，系统各智能体的状态值如图3和图4所示。

图3 x方向上领导者与跟随者的状态Figure 3. States of leaders and followers in x direction

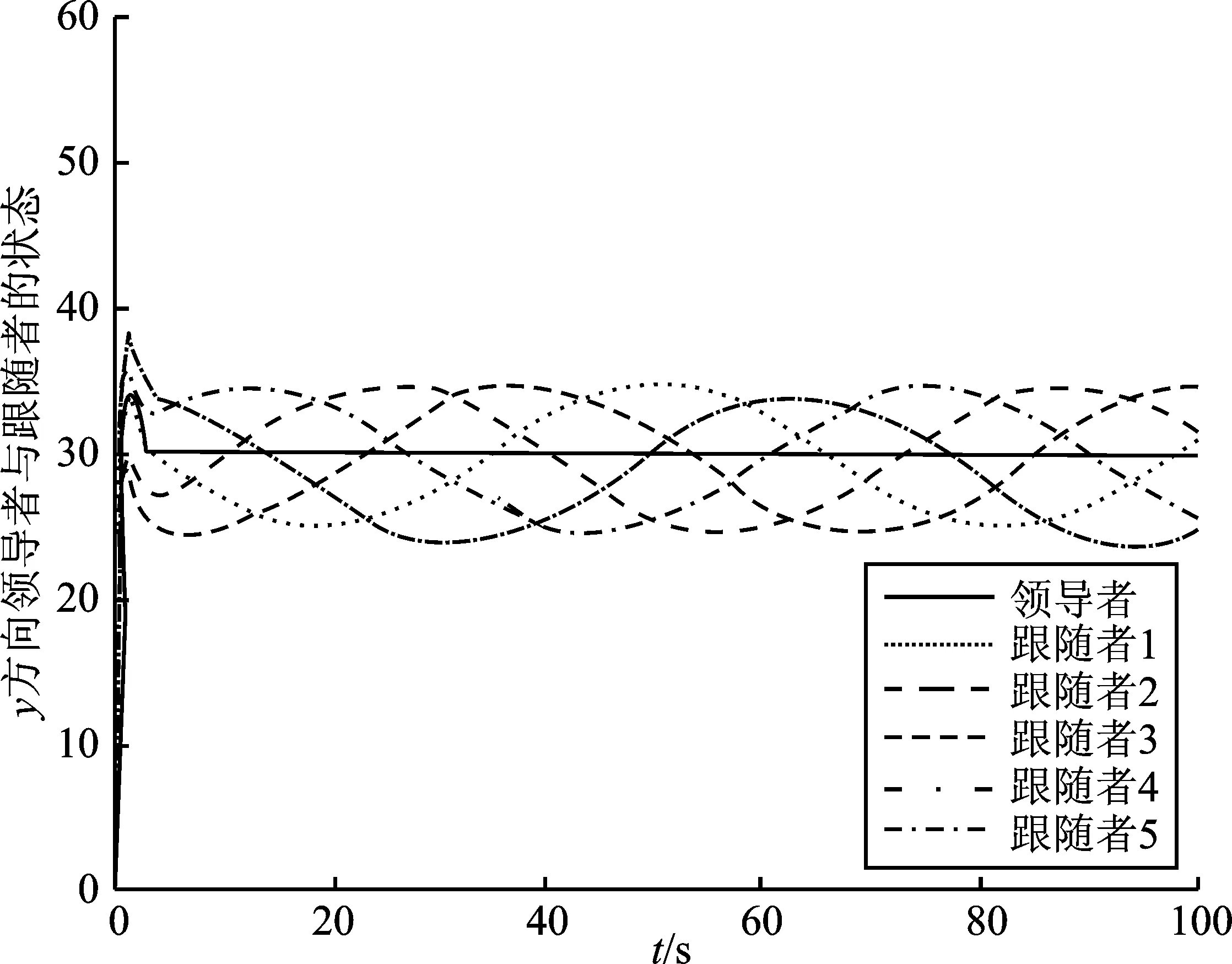
图4 y方向上领导者与跟随者的状态Figure 4. States of leaders and followers in y direction

由图3和图4可知，领导者在控制协议下能够快速趋于所预定的期望值，即在x轴方向上趋于给定领导者的期望值20，在y轴方向趋于给定领导者期望值30，且跟随者在跟踪领导者时围绕着领导者做编队运动。在时间为10 s时系统基本稳定，由于存在外部扰动，编队误差不趋于0，而是在一个很小的范围内上下波动。系统编队的形成过程如图5所示。

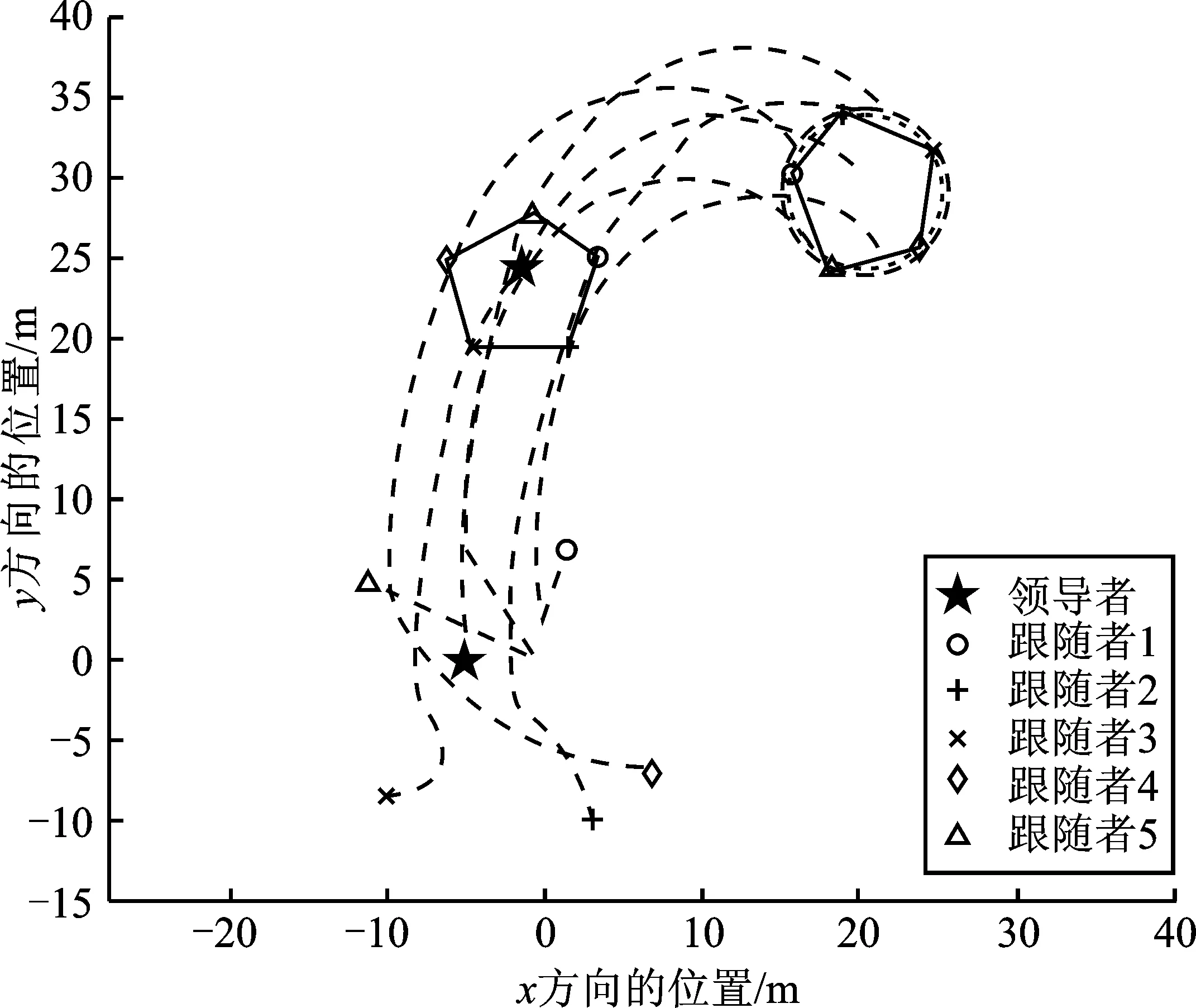
图5 编队位置及其变化Figure 5. Formation position and variation

由图5可以看出，在初始时，领导者与跟随者在二维空间中呈随机分布，与期望的正五边形编队形状相差较大；在所设控制协议的作用下，跟随者在时间为30 s时已经形成了比较规则的编队形状；当领导者到达最终期望位置时，跟随者的误差将稳定在一个有界范围内，并且跟随者围绕着领导者做圆周运动，形成了期望的正五边形编队形状。

5 结束语

异构集群系统可以有效扩展同构集群系统在功能上的多样性。针对异构线性集群系统，本文在有向拓扑结构下设计了一种分布式PI控制协议。本文使用领导者-跟随者的方法，研究了更具实际使用价值的异构集群系统的编队控制问题，使用李雅普诺夫稳定性分析理论给出了时变编队形成的充分条件，并给出了一致性误差最终一致收敛的残差集。针对在实际应用场景中多智能体系统受到外部未知有界扰动影响的情况，本文证明该控制协议能够保证集群系统编队跟踪误差最终一致有界，因此具有一定的鲁棒性。本文所的出的结论可被推广到具有无向拓扑结构的多智能体编队跟踪控制问题中，也可用来解决多智能体系统的一致性问题。

但是，本文只研究了具有相同维度的异构多智能体系统的编队跟踪控制问题。在实际的应用场景中，系统中的智能体维度更可能是不同的，因此在未来的研究工作中，需要针对由不同维度组成的异构多智能体系统进行进一步的研究。