基于Zoeppritz方程的纵横波联合反演方法及应用
2023-01-03胡鑫王国权刘俊洲支丽霞陈双全
胡鑫 ,王国权,刘俊洲 ,支丽霞,陈双全
1 页岩油气富集机理与有效开发国家重点实验室,北京 100083
2 中国石化弹性波理论与探测技术重点实验室,北京 100083
3 中国石油大学(北京)CNPC物探重点实验室,北京 102249
4 中国石油大学(北京)理学院,北京 102249
0 引言
目前,石油勘探开发正向深海、深地及非常规等油气资源进军[1]。对于这类油气资源的勘探开发,所面临的地球物理问题变得越来越复杂,需要提供更为丰富和准确的油藏储层特征描述和相应的油气检测资料。因此,面向叠前道集数据的地震反演方法已经成为油藏储层预测及流体检测常用的技术手段[2]。此外,根据双相介质理论,地下岩石中储层参数的微小变化会直接影响到地层的弹性模量,因此,结合地震岩石物理理论,叠前反演同样可以实现对含油气储层的定量解释[3]。考虑叠前反演方法与各向异性理论的结合,反演得到的各向异性参数也有助于裂缝、缝洞型碳酸盐岩和页岩等复杂结构储层的裂缝预测[4]和地层压力[5]、岩石脆性[6]以及地应力的反演[7]。并且,随着OVT(Offset Vector Tile)域五维数据采集和处理技术的发展,利用叠前地震反演方法开展储层预测和流体解释的精度将进一步提升[8]。
叠前地震反演方法的理论基础是Zoeppritz方程,该方程准确地建立起了平面波入射到界面处产生的反射与透射波之间的关系式。但是,由于Zoeppritz方程的强非线性,将其直接应用到实际地震数据反演中较为复杂,因此早期的地震反演一般采用Zoeppritz方程的近似公式。Aki和Richards在假设入射角角度较小且界面两侧弹性参数变化不大的情况下,利用射线参数与速度之间的关系,得到了一个新的用于描述反射系数与纵横波速度及密度间关系的表达式,这个新的近似式被称为Aki-Richards近似公式[9]。利用该近似式,相对简化了叠前地震数据的反演过程,可以稳定地获得较为准确的速度和密度等参数。因此,目前常规的叠前地震反演方法技术均是基于简化的近似公式进行的,并在许多商业化的叠前地震反演软件中应用广泛[10]。此后,众多学者对简化方法进行研究并形成了不同的表达式,如Shuey近似式[11],Smith加权叠加方法[12],Fatti等反演纵横波阻抗的AVO(Amplitude Variation with Offset)近似式[13]。Gary等建立的弹性参数反演公式,是目前另一种常用的近似公式[14]。
随着复杂油气储层逐渐成为油气勘探的主要目标[15-21],常规的AVO叠前反演方法已逐渐不能满足其更高精度的要求,其中尤为突出的问题是密度反演的不稳定性。Downton和Ursenbach很早即在研究中指出大偏移距数据的缺失会损失叠前反演中剪切模量和密度的精度[22],而对大偏移距、大角度数据的处理能力正是Aki-Richards等一系列近似式所不具备的。此外考虑到单阻抗界面反射差异的问题[23],降低近似方程因假设条件限制带来的模型误差,拓展现有的反演理论与方法同样非常关键。因此,选择精确的Zoeppritz方程直接构建反演目标函数,以提高反演的稳定性和对实际数据的适用性,已经成为当前的研究重点和难点之一。早期的研究集中于将Zoeppritz方程改写为一个由四个独立的比值参数组成的形式[24-25],新的形式显著降低了原方程的强非线性,使得直接采用线性反演策略成为可能,但该方法并不能直接得到地下的弹性参数,因而引入了一定的不确定性。随着正则化和贝叶斯理论等反演方法的进步,基于Zoeppritz方程的叠前参数直接反演也逐渐得到发展。正则化方法通过在最小二乘方法的基础上增加不同的约束项,有效增强反演算子的稳定性。Zhi等通过采用IRLM(Iteratively Regularized Levenberg-Marquardt)方法,实现了叠前三参数的直接反演,算法整体表现出了很好的鲁棒性[26]。Song等在此基础上通过改写精确形式的Zoeppritz方程,实现了杨氏模量和泊松比的高精度同时反演[27]。Ali等提出了约束非线性AVO反演方法,结合IRLM与Split-Bregman方法,能很好地反演出弹性参数[28]。基于贝叶斯理论的反演方法同样应用广泛,考虑到柯西分布能够促进反演结果的稀疏性,张丰麒等提出了基于柯西分布的精确Zoeppritz方程线性反演方法,有效提升了反演的精度,取得了不错的效果[29]。
考虑到横波对岩石孔隙中流体的变化不敏感,更能反映岩石骨架的性质,可以提高构造解释的精度,因此同时考虑纵横波的联合反演策略可以很大程度上减少反演结果的多解性。但考虑到横波勘探成本的昂贵,且由于横波能量衰减较快导致纯横波数据信噪比较低,因此目前依然广泛采用纵波激发、三分量检波器接收的转换波勘探开展纵横波联合反演[30]。Stewart最先提出纵横波联合反演的方法,将加权叠加方法推广到联合反演进而获得纵波速度比和横波速度比等参数[31]。陈天胜等围绕P波和P-SV波的反射系数近似方程提出了一种基于方向加速度最优化的速度比值同时扫描的纵横波联合反演方法[32]。纵横波联合反演也逐渐被应用于流体识别、储层刻画等[33-35]。随着基于Zoeppritz方程的纵波反演方法的兴起,基于精确方程的联合反演方法也逐渐成为学界研究的热点,并取得了一定的效果[36-40]。
本文基于精确Zoeppritz方程,计算得到的纵波反射系数以及转换波反射系数,解决了反射系数近似公式的各种假设条件的限制,降低了模型带来的不确定性,同时利用多波资料进行联合反演,避免了反演过程中带来的多解性问题。在反演过程中,采用IRLM方法,合成数据的测试结果表明该方法的抗噪性强且对于初始模型的依赖性较低。最后将该方法应用于实际数据,井旁道的对比表明该方法能取得较为可靠的反演结果。
1 方法原理
1.1 正演模型
本文采用精确Zoeppritz方程来建立弹性参数与地震观测数据之间的联系,利用褶积模型进行正演模拟。Zoeppritz方程描述了入射平面波在水平界面发生波的反射、透射与入射角之间的关系,反射系数及透射系数的大小可以表示成Zoeppritz方程。入射平面波为纵波时,Zoeppritz方程可以表示成:
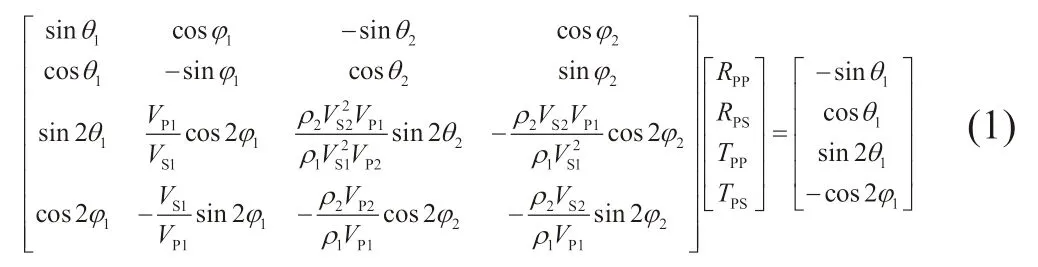
其中,RPP,RPS,TPP,TPS分别表示纵波反射系数、横波反射系数、纵波透射系数和横波透射系数;VP1和VP2、VS1和VS2、ρ1和ρ2分别表示界面两侧地层介质的纵波速度、横波速度、密度,θ1和θ2分别为纵波反射角和透射角,φ1和φ2分别为横波反射角和透射角,下标数字“1”代表上覆地层,下标数字“2”代表下覆地层。
根据Snell定律,射线参数与速度和角度满足以下关系
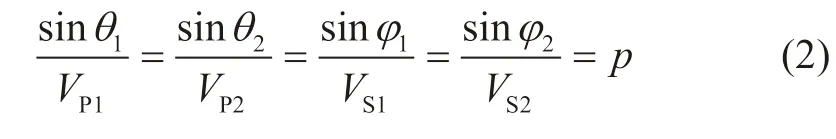
式中,p表示射线参数。Zoeppritz方程精确描述了波的反射系数、透射系数与介质参数VP1, VP2, VS1, VS2, ρ1, ρ2和入射角与透射角之间的关系式。为了能够利用Zoeppritz方程进行反演得到地层参数,需要将Zoeppritz方程(1)中的反射系数表示成解析表达式的形式。根据Aki和Richards给出的PP波与PS波的反射系数解析式,设模型参数的比值r=[r1,r2,r3,r4]T,其中

纵波反射系数RPP、转换波反射系数RPS可以写成:
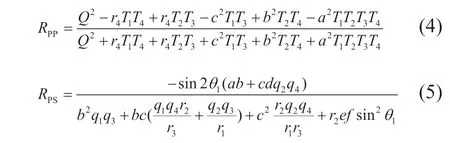
其中,
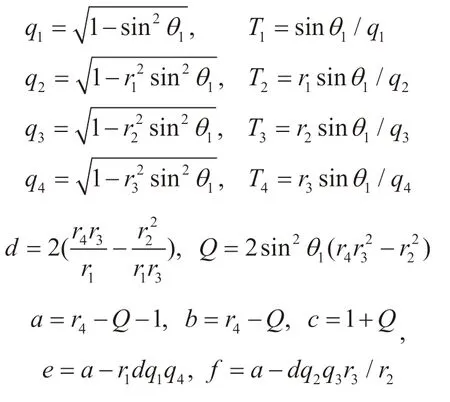
公式(4)(5)给出了基于精确Zoeppritz方程得到的纵波与转换波反射系数表达式。根据褶积模型,叠前不同角度的道集数据可以看成是地震子波与地层反射系数序列的褶积,即

1.2 纵波与转换波联合反演
地球物理反演是根据观测数据与正演模型建立目标函数进行迭代求解的过程,本文采用Levenberg-Marquardt方法,并运用正则化思想解决Zoeppritz方程求解的非线性和不适定问题。
1.2.1 反演目标函数
首先根据褶积模型,将对应的PP和PS波数据的正演过程写成矩阵形式为:

因此,利用PP波和PS波叠前道集数据进行联合反演,其目标函数

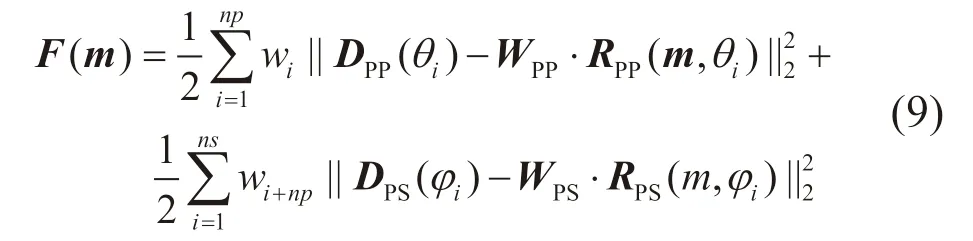
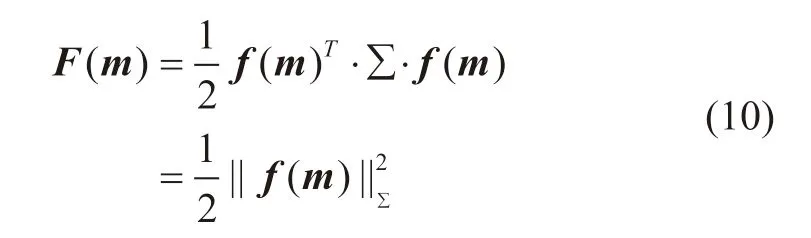
其 中,Σ=diag(λ1,λ2,… , λnp+ns)。联 合 反 演 目 标 函 数(10)中,λi(0 <λi<1)代表加权因子,可以根据井旁道的反演测试结果定性地选择相应的权值。
1.2.2 IRLM反演方法
IRLM方法是求解非线性、不适定反问题的一个十分有效的算法。因此,采用IRLM方法来求解PP波和PS波联合反演问题式(10)。对目标函数式(10)进行IRLM方法求解,


再根据迭代更新,得到当前第k次迭代后的估计值
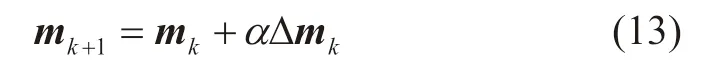
其中,α是步长。
上述向量函数f m()的Jacobi矩阵,可以对向量值函数f m()两边关于m求偏导,得
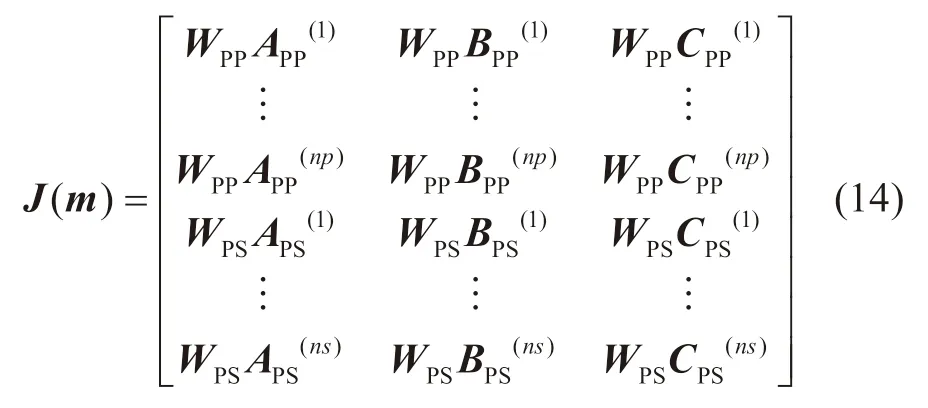
其中,WPP,WPS是PP波与PS波对应子波的矩阵形式,APP(j)表示PP波反射系数相应于入射角θj关于纵波速度的偏导数构成的子矩阵;BPP(j)表示PP波反射系数相应于入射角θj关于横波速度的偏导数构成的矩阵;CPP(j)表示PP波反射系数相应于入射角θj关于密度的偏导数构成的子矩阵;APS(j),BPS(j),CPS(j)分别表示PS波反射系数相应于入射角θj关于纵波速度的偏导数、横波速度的偏导数和密度的偏导数构成的子矩阵,其具体的表达式见附录A。具体算法流程如下:
1、给定模型参数的初值m0,ε,ρ,η,σ最大迭代次数kmax,令k = 0;
2、计算目标函数f (m0)和梯度g0=∇f (m0),判断是否满足终止条件(15)

3、令k k=+1,如果k<kmax,执行以下步骤
1)解方程(16)

2)利用强Wolf条件(17)和(18)确定步长α
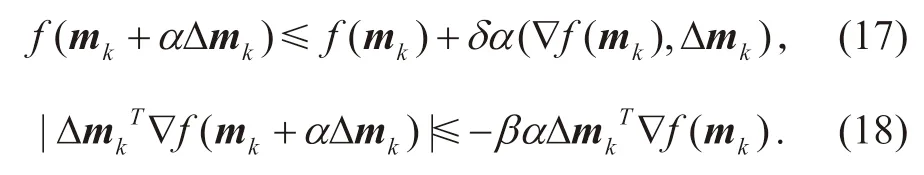
其中δ∈(0,1),β δ∈(,1),本文取δ=0.0001,β=0.9。
3)利用式(19)更新模型参数

4)计算目标函数f (m0)和梯度gk+1=∇f (mk+1),判断是否满足终止条件式(18)和式(20)

5)根据式(21)和式(22)更新μk和λk,迭代停止前继续步骤3
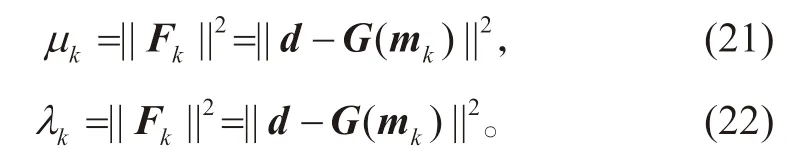
2 合成数据测试
为了验证联合PP和PS波数据进行精确Zoeppritz方程的叠前反演方法的正确性及可行性,采用某实际测井数据合成叠前的PP和PS波道集数据。如图1a所示为实际测井数据曲线,图中包括纵波速度、横波速度和密度曲线。合成道集数据是根据Zoepprtiz方程计算得到不同角度的PP波反射系数和PS波反射系数,再进行与地震子波褶积得到,合成数据的不同角度范围均采用相同的地震子波。如图1b所示为最小相位子波[41],子波的采样间隔为2 ms,长度为200 ms。
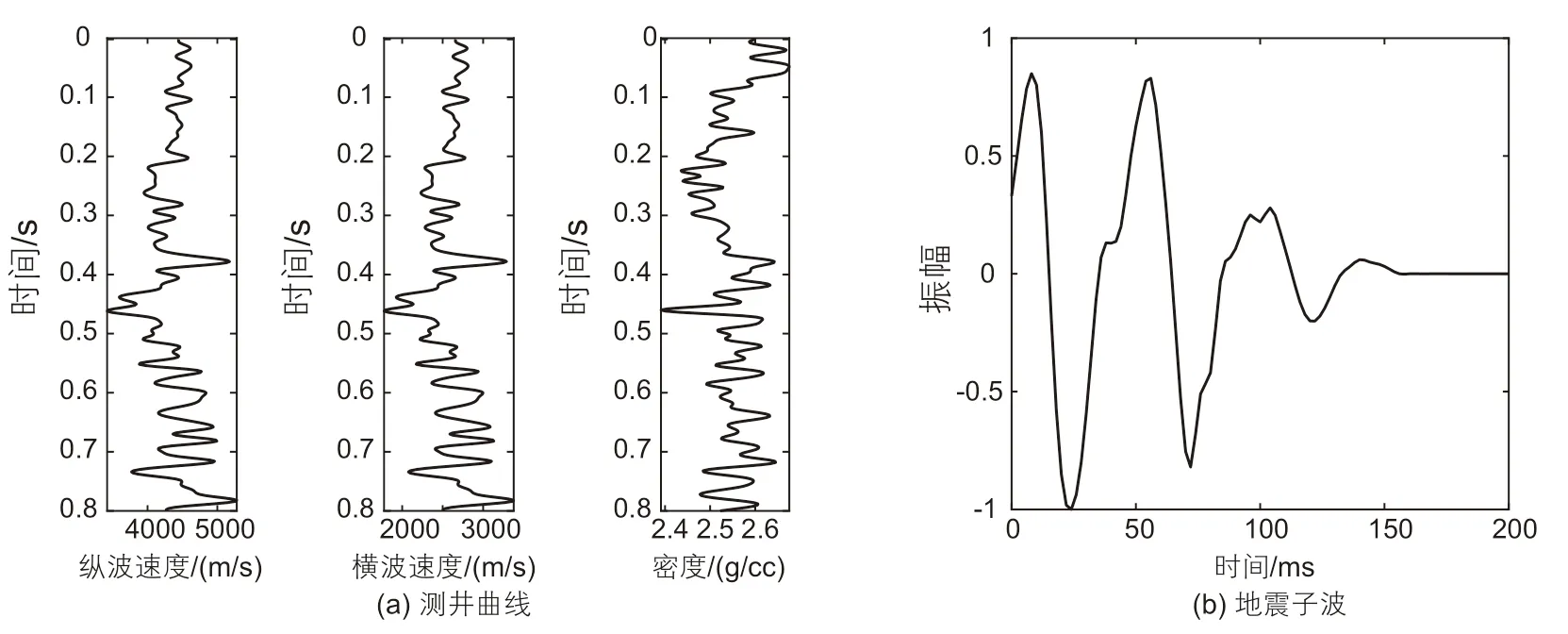
图1 模型数据Fig. 1 Model data (a) well logging curves; (b) seismic wavelet
由于纵波正演模拟时,使用近似方程作为正演算子时会产生理论误差[42]。考虑到转换波正演模拟,也会产生理论误差,如图2所示,图2a是精确Zoeppritz方程合成的PS地震记录,图2b是Aki-Richards近似方程合成的PS地震记录,图2c是两者的理论误差。据此分析,精确Zoeppritz方程与Zoeppritz近似方程在正演过程存在的理论误差,可能会导致在反演过程中反演结果精度下降。因此直接采用精确Zoeppritz方程进行反演,可以提高反演结果的精度,较Zoeppritz近似方程更有优势。
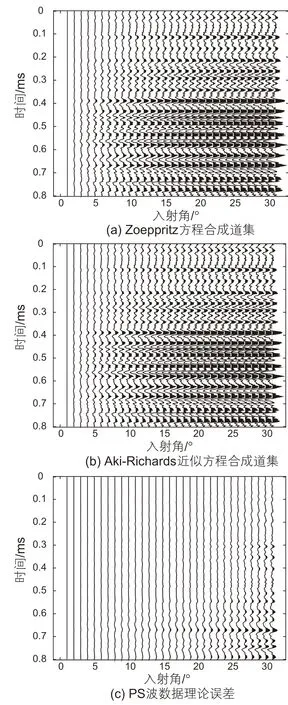
图2 PS波合成角道集数据及误差对比Fig. 2 Comparison of PS-wave synthetic gathers and data error (a) Zoeppritz equation; (b) Aki-Richards approximate equation; (c) gather data error
在反演过程中,小的扰动会造成反演求解产生很强的不适定问题,为了验证本文方法具有较强的稳定性,能很好地解决非线性问题,因此模型测试中加入不同信噪比的噪声,合成相应的地震记录。合成地震记录如图3所示,图3a、3b、3c分别为PP波角度域无噪声记录、信噪比为5与信噪比为2的含噪声记录;图3d、3e、3f分别为PS波角度域无噪声记录、信噪比为5与信噪比为2的含噪声记录。可以看出,由于噪声的加入,极大增加了合成地震记录的扰动性,会导致反演求解产生很大的不适定问题。

图3 不同信噪比PP波及PS波道集数据对比。PP波道集: (a)无噪声; (b)信噪比为5;(c)信噪比为2;PS波道集: (d)无噪声; (e)信噪比为5;(f)信噪比为2Fig. 3 Comparison of PP- and PS-waves synthetic gathers with different SNRs. PP-wave gathers: (a) no noise; (b) SNR=5; (c) SNR=2; PS-wave gathers: (d) no noise; (e) SNR=5; (f) SNR=2
图4给出了利用本文方法对模型数据反演得到的结果,分别进行了PP-PS波联合反演与PP波单独反演,反演中均采用了IRLM方法求解。其中,图4a为无噪时的反演结果,图4b为信噪比为5的反演结果,图4c是信噪比为2的反演结果,图中的黑色曲线代表初始模型,墨绿色曲线代表真实模型,红色曲线代表反演结果。对比图4的反演结果,在随着数据噪声加大时,不管是PP波与PS波联合反演还是PP波单独反演,整体反演结果仍然与真实结果吻合较好,信噪比为2时,亦能趋于稳定,与信噪比为5时反演结果无明显差别,特别是纵波速度与横波速度。为了凸显联合反演的优势,计算了PP-PS波联合反演以及PP波单独反演的相关系数以及平均相对误差,如表1所示,信噪比为5到信噪比为2时,相关系数与平均相对误差逐渐趋于稳定。但是密度反演结果,随着噪声的加强,与实际井数据有着一定的偏差,主要原因是由于密度曲线的反演需要更多的大角度范围数据,而模型测试仅使用了三个角度的数据进行反演,而且密度项受噪声影响很大。由于整体的反演效果较好,可以很好地解决反演时精确Zoeppritz方程带来的强非线性与不适定性,同时具有很好地抗噪性。因此,利用合成数据测试结果验证了提出的反演方法的可行性。

表1 反演结果的相关系数与平均相对误差对比Table 1 The comparisons of correlation coefficients and average relative error between the inversion results
3 实际数据应用
最后,将该反演方法应用到实际地震数据的PP波与PS波联合反演中,验证文中提出的反演方法在实际数据反演中的适用性。对于实际数据,叠前纵波与转换波资料分别是纵波时间域与转换波时间域的角度道集数据。由于转换波的旅行时经过纵波速度入射、横波速度出射得到,而纵波的双程旅行时均是纵波速度,因此同一反射层的反射PS波和PP波的双程旅行时不同,因此,需要对其进行时间域的匹配[43]。图5为转换波时域匹配前后的数据及纵波叠后剖面的展示,图5a是转换波匹配前的剖面,时间范围是1.0~5.5 s,图5b是时域匹配后的转换波叠后剖面,时间范围变到了0.7~3.8 s,图5c是纵波叠后剖面。可以看到未匹配前的转换波剖面与纵波剖面,在时间轴上差异很大,同相轴完全对应不上。而在经过时间域匹配之后,对比图5b和图5c,可以看到两个剖面整体上同相轴比较一致。图6为匹配后3个CDP道集对比结果,分别对应CDP号为499~501,每个CDP道集有10个角度道(5°~32°),图中显示的时间范围为目的层段范围(1.2~2.0 s),尽管转换波地震记录信号偏弱,但是可以看到在1.3 s、1.6 s和1.9 s处,纵波与转换波的主要同相轴可以大致对齐,波形也大致可以对齐。
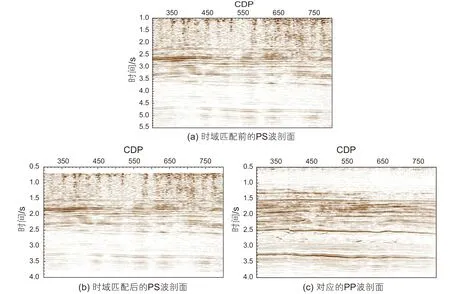
图5 PS波时间域匹配前后叠加剖面对比Fig. 5 Stacked sections comparsion of PS-wave time registration (a) PS-wave section before time registration; (b) PS-wave section after time registration; (c) the corresponding PP-wave section

图6 时间域匹配后叠前道集数据对比Fig. 6 Comparison of gathers before and after time registration (a) PP-wave pre-stack gathers; (b) Time domain registration PS-wave pre-stack gathers
为了验证时域匹配的效果,采用互相关时延谱进行计算验证,图7为时域匹配后转换波数据与纵波数据的互相关时延谱,在整个时间段上,最深的红色集中在零延时处,其相关系数最大,说明转换波数据很好地匹配到纵波时间域。
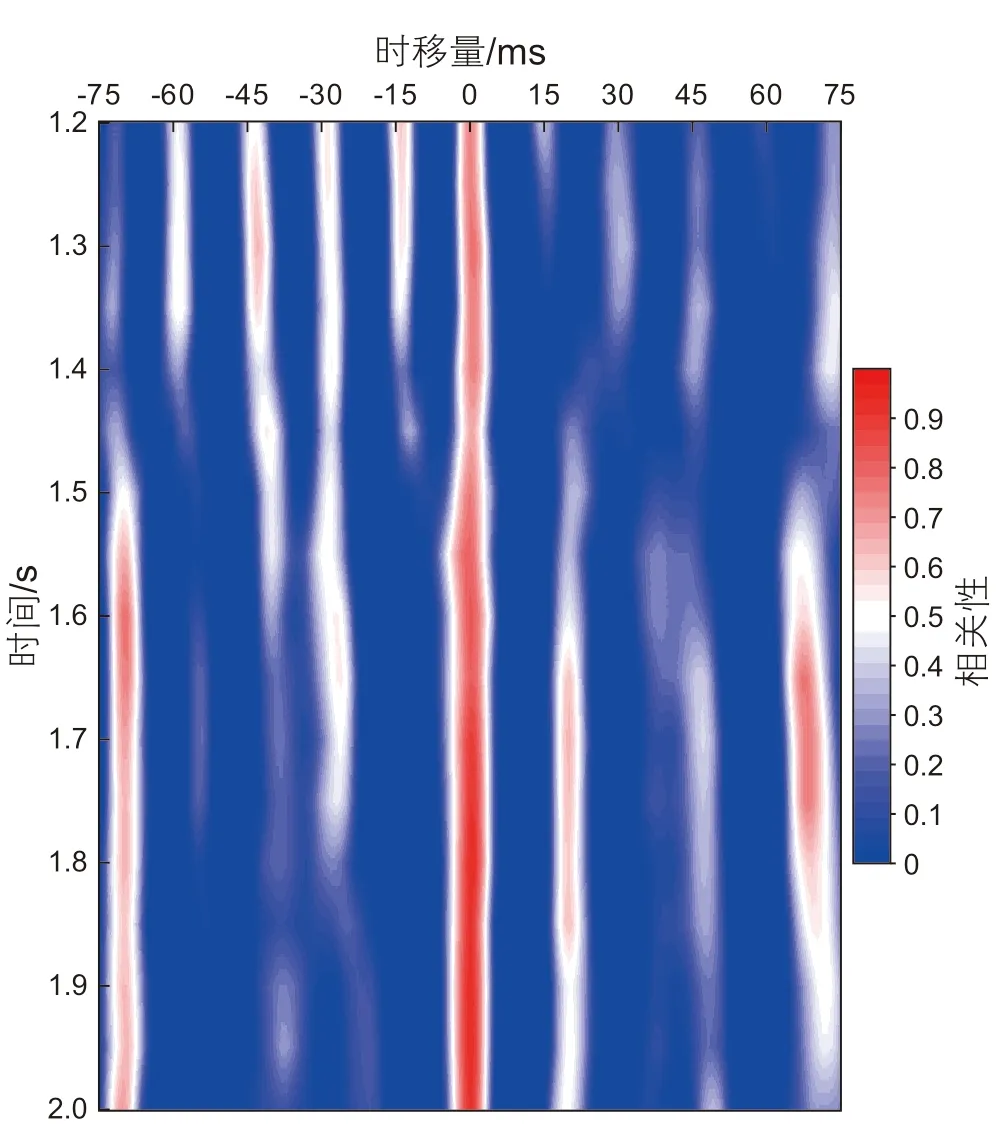
图7 时域匹配后转换波与纵波数据的互相关时延谱Fig. 7 Cross-correlation time-shift spectrum of the registration PS-wave and PP-wave data
图8为匹配后的PP波与PS波分角度叠加的实际地震剖面,图8a从上到下依次是分10°、20°、30°叠加的纵波叠后剖面,图8b从上到下依次是分10°、20°、30°叠加的转换波叠后剖面,由于转换波本身数据质量不如纵波数据,因此转换波叠后剖面的成像质量不如纵波叠后剖面,尤其是根据小角度叠加的剖面。但是,通过对比发现,尽管转换波成像质量不佳,但匹配后的效果来看,纵波剖面与转换波剖面的主要同相轴是一致的,匹配后的数据能够满足联合反演的要求。

图8 三个角度部分叠加剖面对比,三个角度分别为10o,20o和30oFig. 8 Comparison of three different partial stacked sections of angle gathers, the angles are 10o, 20o and 30o, respectively PPwave sections and PS-wave sections
利用IRLM算法进行了PP波单独反演,分别反演得到相应的纵波速度、横波速度与密度,如图9所示。通过将井数据插入到反演结果剖面中,反演结果与井数据的一致性较好。而且,通过计算井旁道反演结果与测井数据的纵波速度、横波速度和密度的归一化均方根误差(Normalized Root Mean Square error, NRMSe),其值分别为0.6%、0.62%、0.28%。说明本文提出的基于IRLM算法的演方法具有较强的抗噪性,有效保证了叠前反演的稳定性。

图9 PP波单独反演结果对比,图中分别插入了井曲线Fig. 9 The inverted results only using PP-wave gathers. The well-logging curves of velocity and density are inserted in the sections (a) P-wave velocity; (b)S-wave velocity; (c) density
图10为利用本文方法采用联合反演方法得到的纵波速度、横波速度及密度剖面,反演结果稳定,剖面特征与原始地震数据剖面一致,而且横波速度剖面和密度剖面的结果较好。为了对比反演结果的准确性,图10中加入了实际井数据的纵波速度、横波速度及密度曲线,将测井数据按相同的色标进行变密度显示,井旁道反演结果与测井数据的纵波速度、横波速度和密度的归一化均方根误差分别为0.69%、0.28%、0.12%。通过对比反演结果与井数据结果,可以看到反演结果与井的一致性较好,特别是密度曲线的反演结果。
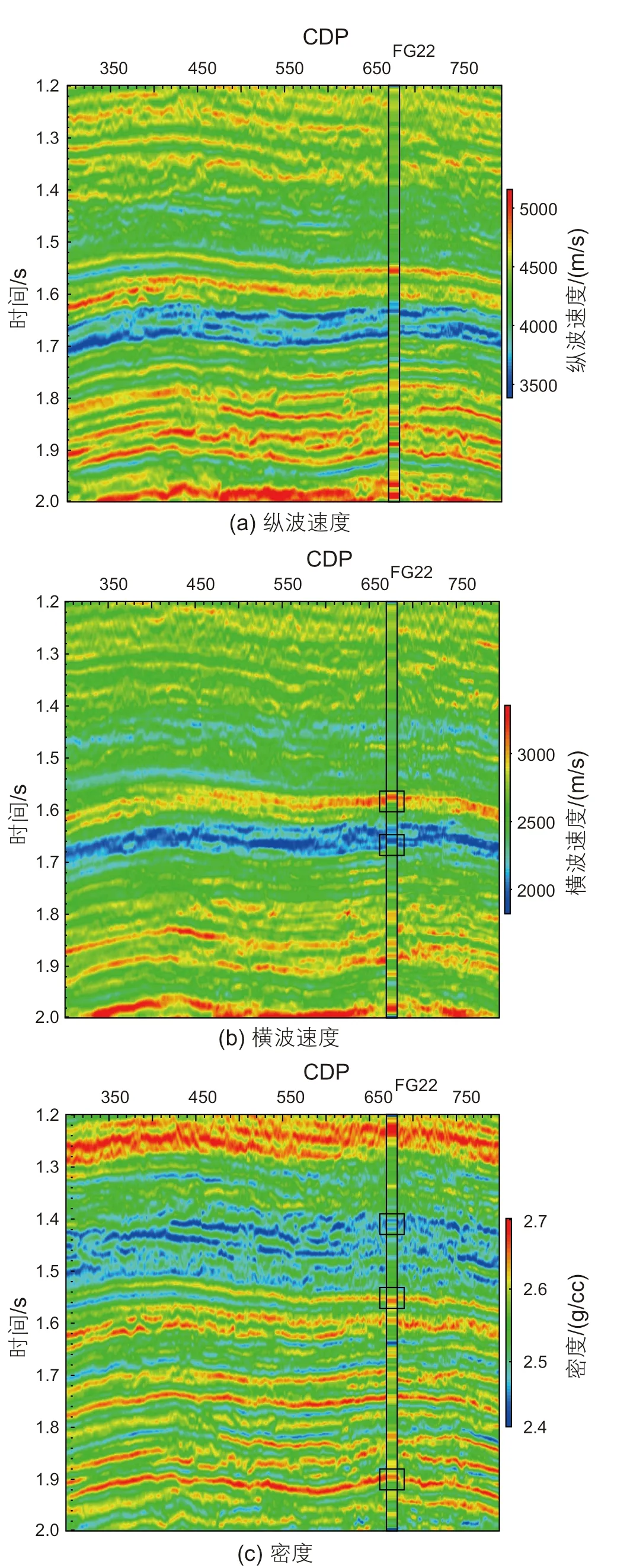
图10 采用IRLM方法反演结果,图中分别插入了井曲线Fig. 10 The inverted results by IRLM method. The welllogging curves of velocity and density are inserted in the sections (a) P-wave ; (b) S-wave velocity; (c) density
为了进一步验证本文方法的有效性,对比了与商业软件的常规联合反演结果。如图11所示,分别为用软件反演得到对应的纵波速度剖面、横波速度剖面和密度剖面。从图11可以看到,纵波速度反演结果较好,波阻抗特征横向连续性清晰,与井数据也能很好地对应上,井旁道反演结果与测井数据的纵波速度、横波速度和密度的归一化均方根误差分别为0.61%、0.83%、0.31%。但是,反演得到的横波剖面整体与纵波一致,具有一定的相关性,且井数据的对应存在较大的误差。而且,相对于纵横波速度剖面,密度反演结果要更差一些,横向连续性也不清晰。

图11 常规反演方法反演结果Fig. 11 The inverted results by conventional inversion method (a) P-wave velocity; (b) S-wave velocity; (c) density
对比图9、图10以及图11,反演结果中横波速度剖面的黑色方框标记处,可以看到本文方法反演得到的速度剖面与测井数据有较好的对应关系,而常规方法反演的结果不理想,在典型的高速位与低速位与井数据对应不上;而且对于密度剖面,本文方法反演得到的剖面特征横向连续性清晰,与井数据的一致性较好,常规方法反演结果与井数据一致性低。而且,纵横波联合反演在精度和抗噪性上要高于PP波单独反演,能更好地解决反演的不适定问题,尤其是密度项反演的抗噪能力较强。
4 结论
采用基于Zoeppritz方程的精确PP波与PS波反射系数表达式,建立起了基于PP波与PS波叠前道集数据的纵横波联合反演方法,推导了详细的偏导数表达式。同时,在反演求解过程中,采用IRLM反演方法可以很好地解决纵横波联合反演的强非线性与不适定性问题。合成数据验证了本文方法的有效性,并且通过含噪数据测试了算法的抗噪能力。在实际数据的反演应用中,本文方法反演的纵波速度剖面、横波速度剖面以及密度剖面,与原始地震剖面保持良好的一致性。相比于常规的方法,有着较好的优势,能弥补密度项本身受噪声影响较大的缺陷,并且反演的横波速度与密度剖面效果很好,与对应井数据有着较好的一致性,验证了本文提出的反演方法的适用性。
本文采用的PP波与PS波角度道集数据为不同时间域的数据,在进行实际数据联合反演前,需要利用准确的速度比将PS时间域的数据匹配到PP时间域。因此,基于多波数据的时间域匹配是多波地震数据联合解释与反演的关键核心,而开展深度域的多波数据联合直接反演将是后续研究的重要方向。
附录A:偏导数计算表达式:
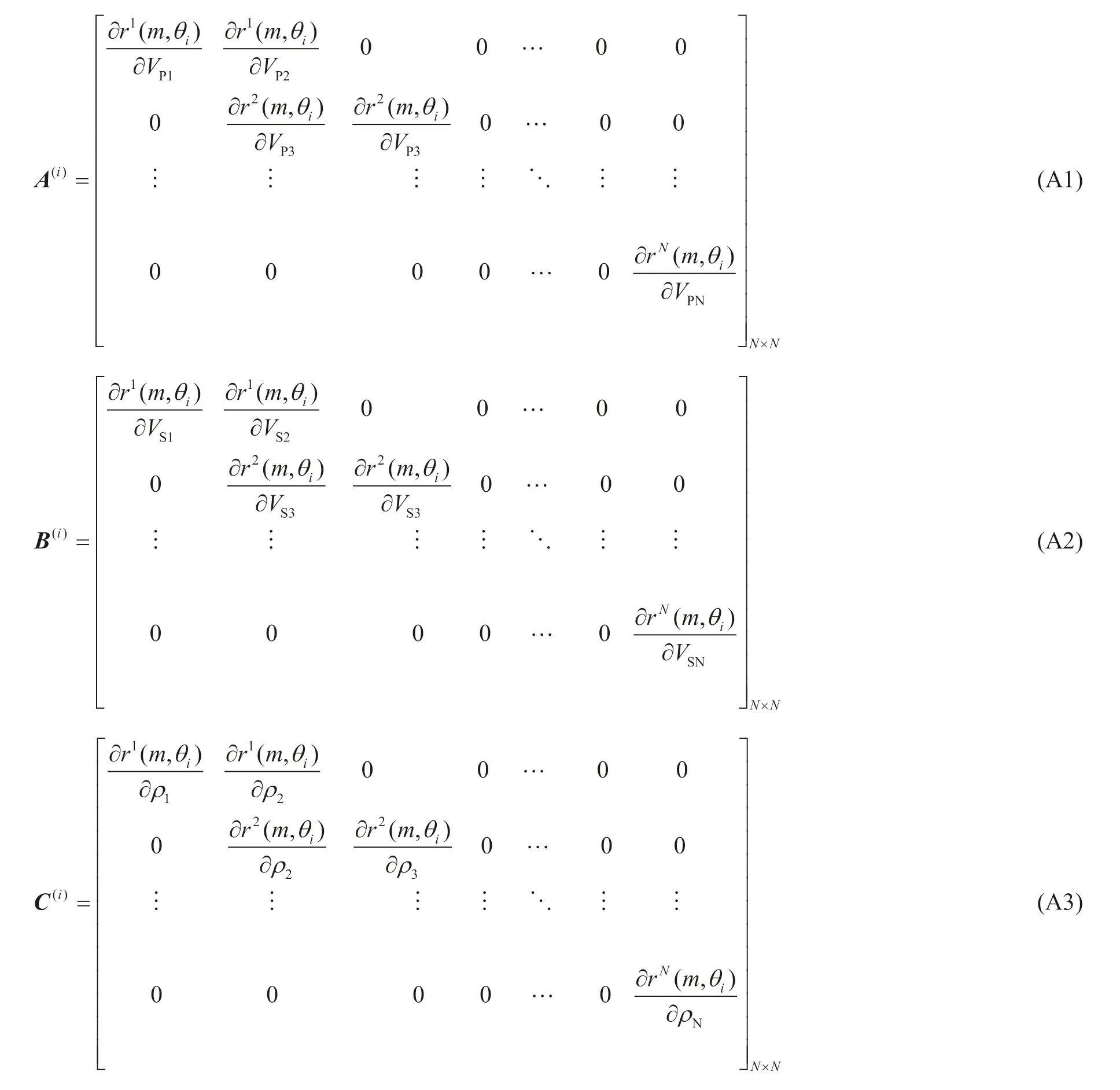
为了计算Jacobi矩阵(14),需要计算反射系数关于速度和密度的偏导数。假设模型参数为了方便,记(1)式的系数矩阵为A,反射系数和透射系数组成的向量为R,右端常数项构成的向量为B,则有矩阵方程

令(A4)式的矩阵方程两边对的m每个分量求导可得



解方程组(A4)和(A5-A18)即可得反射系数对地层参数的偏导数,从而计算得到雅可比矩阵J (m)。
