基于记忆传递旗鱼优化的K均值混合迭代聚类

黄 鹤， 熊 武， 吴 琨， 王会峰， 茹 锋， 王 珺

(长安大学 a. 西安市智慧高速公路信息融合与控制重点实验室;b. 电子与控制工程学院， 西安 710064)

聚类分析是统计学习领域的重要组成部分[1-2]，可以针对不同的对象分析异同，根据数据之间的内在特征，将特征相似度较大的数据样本划分到同一簇.簇内数据相似度和簇间数据的差异性可以反映聚类算法的优劣.K-means聚类(KMC)是使用最广泛的聚类分析算法之一[3]，但在实际应用中KMC初始点比较敏感，选取不当会导致聚类结果误差较大[4].针对此问题，K-means++在一定程度上解决了KMC初始化方面的算法缺陷.另一方面，KMC的优化路径过于简单，存在算法早熟的问题.目前常用解决方案是将模拟退火、遗传算法(GA)和群体智能等启发式算法与K-means相结合，解决局部最优的问题[5-6].群体智能方法是一类仿生物行为计算技术，通过模拟蚁群、飞蛾等生物群体行为搜索最优解.基于群体智能的聚类优化是目前的研究热点，广受研究学者的关注[7-8].文献[7]将改进飞蛾扑火算法与KMC算法交叉迭代实现聚类，由于引入样条插值对飞蛾扑火的改进存在一定的局限，插值结果在很多情况下无法对算法结果进行有效优化，导致算法收敛速度变慢.旗鱼优化器(SFO)是于2019年提出的一种新型优化算法[9]，具有寻优能力强、收敛快的优点，其灵感来自旗鱼捕食沙丁鱼的过程.SFO根据生物行为构建数学模型，模型由两部分组成：一是对目前为止群体最佳个体的搜索，二是生成多样的沙丁鱼种群.SFO通过多次迭代更新旗鱼和沙丁鱼位置求解最优解.两种鱼的更新方式模拟了仿生学路径，实现捕猎中的快速和高精度搜索，优化效果较好.

本文在改进SFO的基础上，与KMC算法混合迭代，提出了一种基于记忆传递旗鱼优化的K均值混合迭代聚类(MTSFO-HIKMC)算法.首先采用最大最小距离积对KMC进行初始化，解决了传统聚类方法的随机性，减少了聚类初始化耗时.同时，设计了自适应记忆传递优化策略，提出一种记忆传递旗鱼优化方法，有效提升了收敛速度和搜索精度，同时避免陷入局部最优.

1 KMC算法的不足

KMC可以将数据集按照不同的类别划分成多个子集，具体步骤如下：① 从n个数据中选取k个对象作为初始聚类中心{Ci};② 计算每个数据到k个初始聚类中心的欧氏距离，根据距离最小原则重新分类数据；③ 计算聚类簇的各个维度平均值，得到新的中心.重复步骤②和③，直到聚类中心不再发生改变或聚类中心发生偏移的距离均小于设定阈值，输出该数据集的聚类中心.

从聚类过程可知，初始聚类中心选择不当会陷入局部最优.聚类中心Cj的计算公式为

(1)

聚类中心Cj与样本数据xi的欧氏距离计算为

(2)

式中：d为聚类中心个数.

因此，KMC的初始化具有随机性，可能会将噪声或异值作为初始中心，导致每次聚类结果相差较大，算法鲁棒性较差[10].同时，简单的更新过程会导致KMC陷入局部最优.

2 MTSFO算法

2.1 SFO算法

2.1.1初始化 SFO的初始化是在给定的搜索空间内随机初始化，包括旗鱼和沙丁鱼的初始化.旗鱼种群和沙丁鱼种群分别用XSF和XF表示.XBSF和XBS是初始化后适应度值最好的旗鱼和沙丁鱼个体.在一个搜索空间内，随机初始化沙丁鱼和旗鱼的比例可以根据数据集的选择进行一定程度的调整，并按照优化函数进行适应度排序，得到最优种群.

设鱼群矩阵M大小为(a,w)，则有

(3)

式中：f11为第1只旗鱼在第1维变量空间的位置；w为搜索空间的特征数，即搜索空间的维数；a为旗鱼和沙丁鱼的总数.假设旗鱼和沙丁鱼的种群比例为3∶7，则旗鱼数量为0.3a，沙丁鱼数量为0.7a.

旗鱼的适应度矩阵FSF大小为(0.3a, 1)，表示为

(4)

式中：fsfp为第p只旗鱼的适应度值.

沙丁鱼的适应度矩阵FS大小为(0.7n, 1)，表示为

(5)

式中：sq为第q只沙丁鱼的适应度值.FSF和FS矩阵为两种鱼群适应度排序之后的结果，这说明沙丁鱼s1是鱼群M在当前迭代搜索中的最优解.

2.1.2旗鱼位置更新机制 更新机制主要可分为旗鱼的追捕过程和沙丁鱼的逃脱引起的位置更新.

(1) 围猎追捕过程.设适应度最好的个体为头鱼，旗鱼依据旗鱼头鱼和沙丁鱼头鱼位置进行空间位置更新，向两种头鱼渐进靠拢，听从头鱼指挥不断更新位置.定义旗鱼位置更新机制为

XNSFi=XBSFi-λi×

(6)

式中：XNSFi为更新后的旗鱼位置；λi为每次更新的步长大小；XBSFi为当前迭代i次时旗鱼头鱼的位置；XBSi为当前迭代i次时沙丁鱼头鱼的位置；XOSFi为上次迭代时的旗鱼位置.步长定义为

λi=2rand(0, 1)PD-PD

(7)

式中：PD为猎物群的密度，表示为

(8)

式中：NSF和NS分别为旗鱼和沙丁鱼的数量.

(2) 沙丁鱼的位置更新.沙丁鱼的位置更新表达式为

XNSi=r(XBSFi-XOSi+AP)

(9)

式中：XNSi为更新后的沙丁鱼位置；r为步长系数；XOSi为在当前迭代次数时沙丁鱼的最佳位置；AP为旗鱼的攻击力度，计算方式为

AP=A(1-2ie)

(10)

式中：A为力度系数，控制旗鱼攻击力度，A从最大值线性递减到0；e为方向系数，调整旗鱼前进方向.当AP≥0.5时，利用式(9)更新沙丁鱼全部位置；当AP<0.5时，更新沙丁部分位置，定义为

α=NSAP

(11)

β=dAP

(12)

式中：α为本次迭代需要更新的沙丁鱼数量；β为本次迭代需要更新的维度数量.

SFO算法流程如下.

(1) 初始化种群和参数.

(2) 计算旗鱼和沙丁鱼的适应度值，并记录最优适应度值和位置.

(3) 分别更新旗鱼、沙丁鱼位置.如果攻击力度A<0.5，计算α，β的值，并且更新部分沙丁鱼位置；否则，更新全部沙丁鱼位置.

(4) 沙丁鱼、旗鱼位置替换.

(5) 计算所有适应度值，并更新记录最优适应度值和位置.

(6) 判断是否满足迭代停止条件，如果满足则输出结果，否则重复流程(2)～(6).

2.2 改进算法

SFO受限于线性的搜索路径，因此搜索精度有限[6].借鉴生物繁衍进化的基本逻辑，提出一种基于记忆传递旗鱼优化算法，设计自适应记忆传递修正策略优化SFO的搜索路径，以加快其收敛速度，提高聚类精度.

2.2.1自适应记忆传递修正策略 群体智能优化中引入样条插值是目前的研究热点[1]，利用历史最优结果进行插值预测，得到优化路径上的未来最优点，并与更新群体智能得到的最优点进行比较，加快迭代速度.然而，考虑到历史最优点受到复杂搜索路径带来的随机性影响，插值结果与真实优化路径通常相差较大，在高维度时尤其明显，预测结果往往不能对最优点进行有效更新.因此，提出一种自适应记忆传递修正策略，修正策略基本过程分为种群繁衍和自然选择.种群繁衍过程为种群遵循父代优秀基因，产生大量携带有优秀基因的个体；自然选择过程为通过人为设计的自然规律淘汰基因不够优秀的个体，筛选出具有最优基因的子代.结合SFO的特点，设计记忆因子使旗鱼群产生子代，以子代个体适应度函数作为衡量旗鱼子代基因优劣的唯一标准， 从中选拔出最优子代，比较最优子代和父代头鱼之间的基因优劣，通过二次择优得到新的旗鱼种群，修正策略步骤如下.

(1) 确定记忆传递算子产生的子代鱼苗的数量和鱼苗群的半径，表达式为

(13)

(14)

式中：N为种群数量；fk为鱼群个体；fmax和fmin分别为当前鱼群适应度最好和适应度最差的个体；m为种群繁衍能力，决定了一个种群产生有效个体的数量，在本文中特指最优父代个体产生子代的数量；σ为记忆因子遗传过程中产生基因变异的剧烈幅度.σ越大，子代与父代个体相似性越小，算法的全局搜索能力越强；σ越小，子代个体与父代个体相似性越大，算法搜索精度越高.父代最优基因个体产生鱼苗的过程是通过在各个维度产生服从均匀分布的随机偏移量获得新的鱼苗，增加算法的多样性.图1为记忆传递算子产生鱼苗示意图.SFO在产生的不同鱼苗之间跳跃，寻找最优子代，对当前旗鱼鱼群进行修正，达到二次优化的效果.其中，Fmax为当前迭代过程中旗鱼个体；Fr为以父代旗鱼个体作为中心点通过记忆传递算子产生的鱼苗位置.

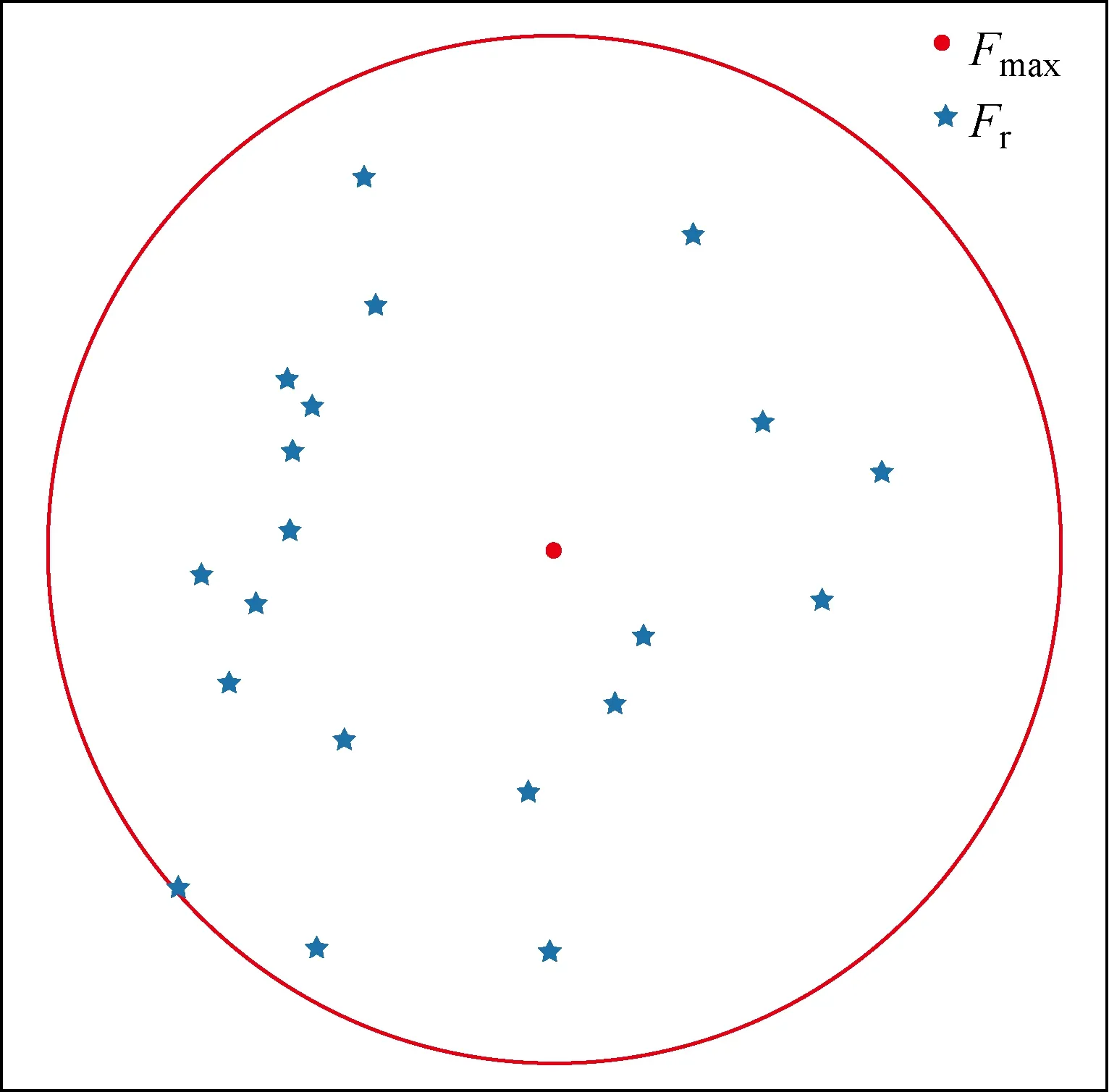
图1 记忆传递算子Fig.1 Memory transfer operator

鱼苗个数取决于父代旗鱼个体基因对环境的适应性，对环境适应更好的个体产生更多的子代个体.鱼苗位置在空间上服从均匀分布，记忆传递规则定义为

(15)

式中：μ为Fmax的向量表示.为了平衡算法的搜索能力和搜索精度，采用自适应的σ定义不同迭代时期的变异剧烈程度，计算方式定义为

(16)

式中：imax为最大迭代次数；h为记忆算子初始阶段的变异幅度.记忆因子可以有效增强SFO的全局搜索能力和局部搜索精度，具体流程如图2所示.

图2 改进旗鱼算法流程图Fig.2 Flow chart of improved sailfish algorithm

MTSFO算法伪代码：

输入: 数据集、聚类数目

输出：聚类中心、分类结果、适应度值

初始化参数

While 不满足终止条件

更新沙丁鱼群和旗鱼鱼群

判断鱼群超出边界:

将样本边界外的值设置为边界值.

结束判断

旗鱼遍历

计算适应度值

结束遍历

沙丁鱼遍历

计算适应度值

结束遍历

按照适应度值对旗鱼和沙丁鱼进行排序

XBSF= 最优适应度旗鱼

XBS= 最优适应度沙丁鱼

更新旗鱼位置

更新沙丁鱼位置

Bp=XBSF

用过适应度值计算S和A1的值

While 迭代次数小于S

根据Bp的位置产生旗鱼后代.

判断后代个体的适应度值优于Bp

由相应后代个体取代Bp的位置.

结束判断

End while

End while

输出：聚类中心、分类结果、适应度值

2.2.2适应度函数选择 适应度函数决定了优化群体进化的方向，直接影响种群算法的优化效果和解的质量[11-12].为使MTSFO更好地优化聚类中心，提升聚类效果，本文采用的适应度函数为文献[7]采用的适应度函数的变体形式，不再以某一类适应度作为评价指标，采用不同簇内适应度总和作为全局适应度去指导算法收敛，适应度函数为

(17)

(18)

式中：AD为全局适应度；Lj为一个种群的适应度；d(xi,Cj)为第j簇内的全体样本到该簇聚类中心的距离之和；Nj为第j簇中的样本数量.从适应度函数可知，当前聚类结果的适应度不仅与每个类别所有样本点到该簇聚类中心有关，也与该类样本数有关，反映的是该簇所有样本点到该聚类中心欧氏距离的均值大小.

3 MTSFO算法与KMC算法的混合迭代

3.1 最大最小距离积优化

采用最大最小距离积方法对KMC进行优化，选取密度较大且分布较稀疏的初始点代替原始算法随机选取初始点，避免初始点选取不当造成的聚类误差[13-14]，改进初始化的步骤如下.

(1) 从数据集M中随机选取1个样本点作为第1个初始点Z1，加入集合Z并从M中删除.

(2) 计算更新后M中所有元素到Z1的距离，选取距离Z1最大的元素为Z2.

(3) 将Z2加入集合Z并从M中删除.

(4) 分别计算更新后M中元素到Z中各个元素的距离，并存入距离矩阵DTemp中.

通过以上步骤可以完成最大最小距离积的初始化，得到的初始聚类中心避免了随机初始化引起的初始误差过大问题，有效减少聚类耗时.

3.2 混合迭代

KMC算法通过迭代求各个维度均值的方法获得聚类中心，其不足在于更新方法过于简单，容易陷入局部最优，导致优化精度过低.利用MTSFO的优化路径替代KMC的优化路径，实现MTSFO与KMC的混合迭代，扩大寻优范围，避免陷入局部最优的同时提高搜索精度.实验证明，此方法能较大提高算法优化效率，主程序流程图如图3所示，算法的基本步骤描述如下.

图3 主程序流程图Fig.3 Flow chart of main program

(1) 输入数据集M，根据数据集类别的个数确定该数据集中类的个数k.

(2) 用最大最小距离积法初始化每个类的中心点.

(3) 计算数据集M中的每个样本点到各个聚类中心的欧氏距离，按数值大小进行排序，将样本点所属类别归于最小欧氏距离的聚类中心.

(4) 使用KMC算法确定每个样本的类别.

(5) 在每个类别的鱼群中通过MTSFO进行寻优操作，得到新的聚类中心.若新得到的聚类中心适应度优于上次迭代的聚类中心，用新的聚类中心代替历史聚类中心.判断当前迭代是否达到结束条件，若未达到结束条件则执行步骤 (4) ，否则循环结束，输出寻优结果，结束程序.

4 实验结果分析与应用

硬件实验平台为i5-6300HQ处理器、GTX-960显卡、12 GB内存的计算机，软件平台为VS Code.

4.1 算法性能评价

为评价MTSFO-HIKMC的改进效果，将MTSFO-HIKMC与IMFO-KMC[7]、K-means++[15]和模糊C均值算法[16]应用到国际标准数据集Iris、Seeds、CMC和Wine中比较性能优劣.算法参数设置如下：每种聚类算法的最大迭代次数都取30次，旗鱼鱼群大小设置为30，旗鱼与沙丁鱼的数量比例设置为7∶3，模糊C均值聚类中的权重指数取2.0.Iris、Seeds、CMC和Wine这4种UCI国际通用测试数据库中的数据集主要特征如表1所示.

表1 标准数据集特征Tab.1 Characteristics of standard data set

MTSFO-HIKMC改进方法分为初始化算法改进和搜索路径优化.为体现不同改进思路对算法起到的作用，利用消融实验分别对算法不同层面的改进进行测试，并与其他算法进行比较，以体现不同改进方法对算法产生的影响.

4.1.1实验一：初始化改进效果评价 为评估最大最小距离积对算法起到的优化效果，采取消融实验分别对初始化优化和搜索路径优化进行实验以验证效果.图4为本文使用的适应度函数来评价IMFO-KMC、K-means++、FCM和结合最大最小距离积的旗鱼K均值混合迭代(SFO-HIKMC)算法的实验结果.从损失衰减数据可知，最大最小距离积法在初始化聚类算法方面有较好的优势，初始点的损失远低于未经过初始化优化的FCM算法，使得优化算法节约起始阶段的迭代次数，对聚类效率有较为明显的提升.从图4可知，适应度衰减曲线明显没有达到最优，尤其在对高维数据集CMC和Wine进行聚类时，最终适应度远高于经典的FCM算法，聚类结果距离数据集最优解还有较远的距离，分析原因是搜索路径单一，聚类结果陷入局部最优导致.

图4 实验一中不同算法在4种数据集上的运行结果Fig.4 Running results of different algorithms on 4 data sets (Experiment 1)

4.1.2实验二：搜索路径改进效果评价 分析上述实验结果可知，通过最大最小距离积改进的算法能够在一个适应度较低的位置开始收敛，使算法能够通过更少的迭代次数收敛到全局最优.但是容易陷入局部最优解，优化精度不足，这与算法本身的搜索路径单一、没有足够能量冲出局部低洼地带有关[17].在实验一的基础上通过自适应记忆传递优化算法对原始搜索路径进行优化得到MTSFO-HIKMC 算法，并与其他几种算法进行对比实验，以验证自适应记忆传递优化策略对聚类算法的优化效果.图5所示为IMFO-KMC、K-means++、FCM和MTSFO-HIKMC算法对不同数据集进行聚类的适应度衰减曲线.由图5可知，在实验一已经陷入局部的SFO-HIKMC算法可以多次跳出局部最优，达到更高的聚类精度.

图5 实验二中不同算法在4种数据集上的运行结果Fig.5 Running results of different algorithms on 4 data sets (Experiment 2)

表2为搜索路径改进前后的算法最终适应度.可知，改进后的算法相较于改进前的算法适应度均有大幅度下降，证明本文改进思路具有实用性.

表2 各类算法在不同数据集上的适应度Tab.2 Adaptability of different algorithms on different data sets

为更客观评价MTSFO-HIKMC改进效果，采用Acc、ARI和NMI共3种评价指标对不同聚类算法进行评估[18-19].其中，Acc表示聚类的准确率，即比较聚类结果是否和真实结果的一致性；ARI为调整兰德系数，用于衡量两个数据分布的吻合程度，值越大表示计算结果与真实值更相似；NMI为归一化互信息，用来表示两组数据之间的关联程度.

表3列出了3种算法实验得到的评价指标，该数据由10次独立实验数据求均值得到.从表中可知，MTSFO-HIKMC在Iris数据集上测得的Acc指标和IMFO-KMC相等且高于K-means++和FCM算法.在Wine数据集测得Acc指标高于其他3种算法.在Seeds和Wine数据集中，MTSFO-HIKMC的ARI指标相较于其他算法均有不同程度提升.可见，MTSFO-HIKMC相较于另外3种算法，在聚类精确度和聚类结果与真实情况的吻合程度方面具有一定优势.

表3 不同算法在4个数据集上的实验结果Tab.3 Experimental results of different algorithms on 4 data sets

表4为4种算法在不同数据集单次迭代所需时间.其中，K-means++和FCM算法单次迭代时间优于MTSFO-HIKMC，而MTSFO-HIKMC消耗的时间成本相较于IMFO-KMC算法在4种测试数据集都有不同程度提升.在数据集CMC和Iris中，MTSFO-HIKMC的单次迭代时间相较于IMFO-KMC算法分别节省了7.82%和6.27%.可见，自适应记忆传递优化策略在提高搜索精度、增强全局搜索能力的同时，造成一定程度上时间成本的增加，但相较于收敛精度相似的IMFO-KMC算法，仍具有一定优势.

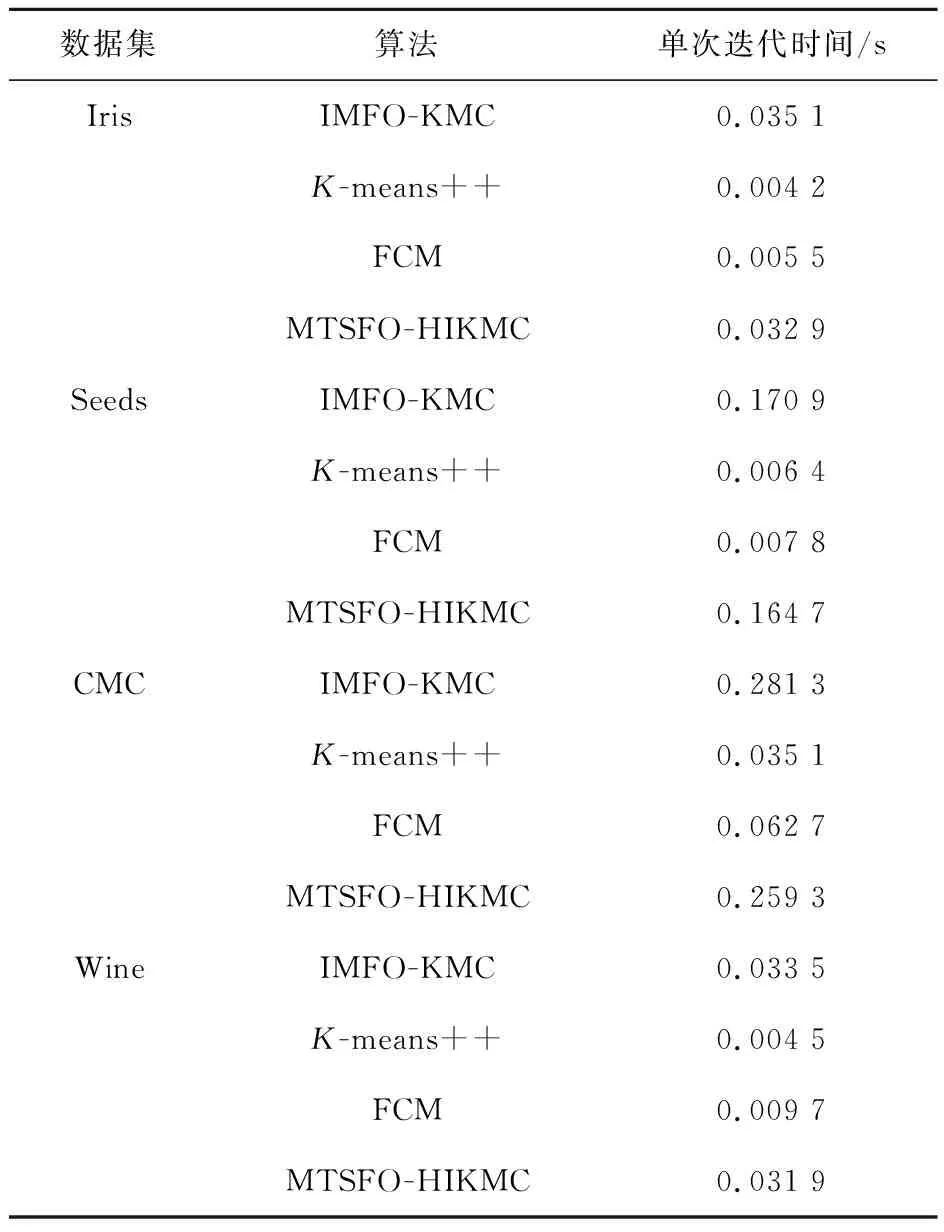
表4 各类算法在不同数据集单次迭代时间Tab.4 Single iteration time of different algorithms in different data sets

分析上述实验结果可知，KMC算法思路简单、聚类精度低、初始聚类中心的随机选取导致算法稳定性差；FCM算法中引入模糊控制的概念，使用模糊聚类算法，使得迭代曲线趋于平滑.但是仍旧存在初始点选取随机性的问题，不仅增加了算法达到全局最优解的迭代次数，而且得到的聚类中心精度不高.IMFO-KMC受限于改进方法，收敛速度提高有限，相较于MTSFO-HIKMC需要更多次迭代去收敛才能达到足够精度；而MTSFO-HIKMC通过最大最小距离积的初始化，减少了到达最优位置的迭代次数，实验一和实验二也证明了自适应记忆传递优化策略使得聚类算法具有较强的全局搜索能力，使聚类算法不易陷入局部最优解，稳定性较强.由表4可知，MTSFO-HIKMC单次迭代算法相较于类似算法具有一定的先进性.由此，可以得出以下结论：MTSFO-HIKMC聚类精度高于传统K-means++算法和FCM算法，在高维数据聚类精度高于IMFO-KMC算法，而在低维数据聚类效果与IMFO-KMC算法接近.在迭代次数和单次迭代所花费的时间成本小于IMFO-KMC算法.本文改进算法具有一定的优越性，在预处理高维数据和实时性要求较高的场合具有较高的实用性.

4.2 测试函数上的性能指标

为了对MTSFO-HIKMC的收敛性有一个更加清晰、直观的了解，分别采用Sphere、Ackley、Three-hump camel、Levy和Bukin函数对MTSFO-HIKMC算法进行测试，并绘制其收敛曲线以直观反映其收敛性能.其中，Sphere和Ackley函数选择在30个维度下进行收敛测试，以反映其高维适应能力，而Three-hump camel、Levy和Bukin这3个函数具有多个局部最优[20]，用以测试MTSFO-HIKMC算法跳出局部最优的能力.图6为各收敛函数在三维可视化图像.

图6 测试函数Fig.6 Test function

图7为MTSFO-HIKMC在5个测试函数迭代60次的收敛情况.可知，在多峰函数上优化算法较早脱离局部最优，在6次迭代完成均已收敛到全局最优；在高维情况下的表现也较好，在30维的Ackley函数上出现3次跳出局部最优的情况，最终收敛于全局最优.由此可知，MTSFO-HIKMC算法在全局寻优能力有较好的表现.

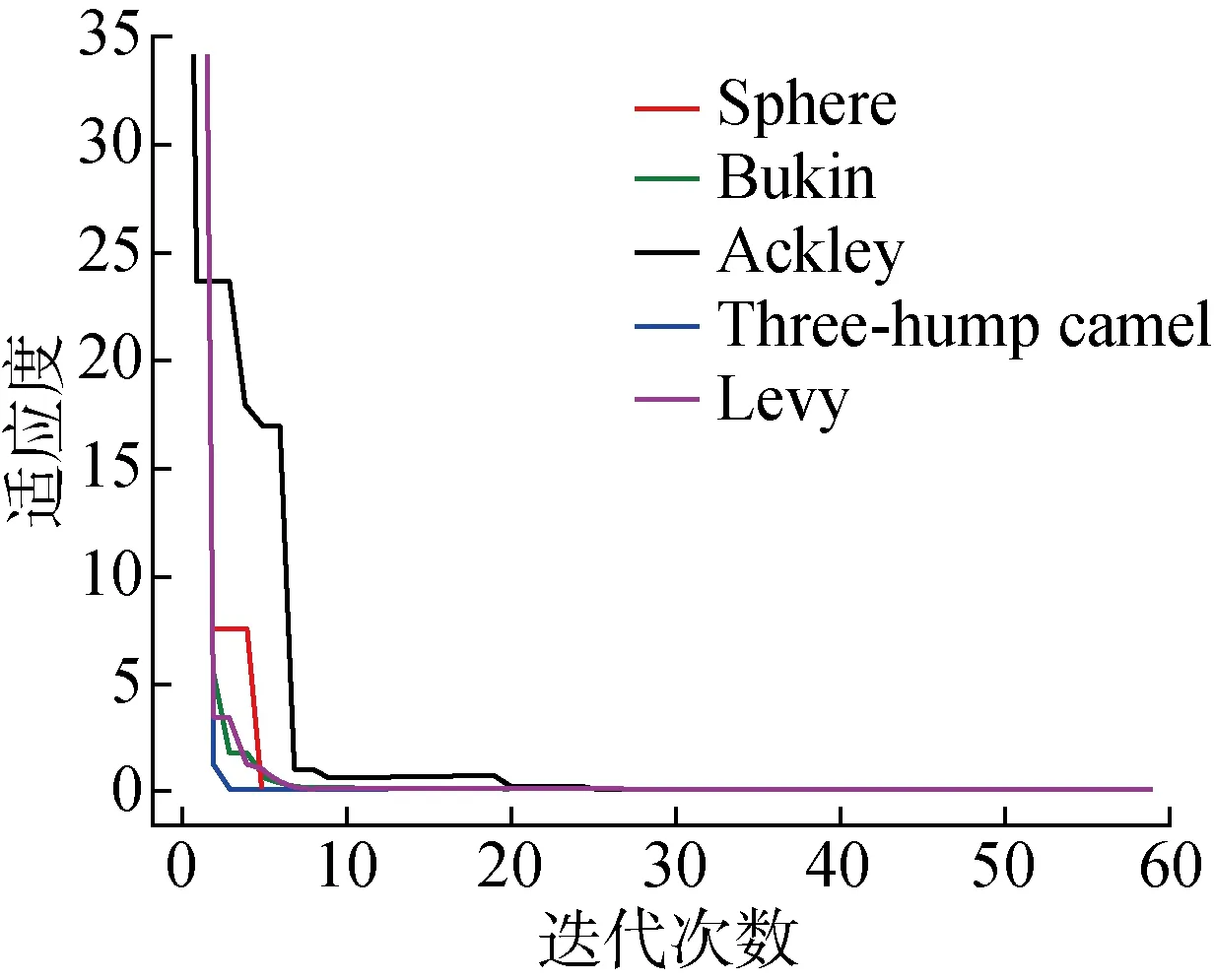
图7 5类测试函数的运行结果Fig.7 Running results of 5 types of test functions

表5为MTSFO-HIKMC算法在5个测试函数上的收敛精度，数据为30次实验取得的均值.其中，MTSFO-HIKMC在高维数据和多峰函数搜索精度较高，尤其是在具有多个局部最优解的Bukin函数上，搜索精度依然非常高.可知，自适应记忆传递优化策略针对跳出局部最优的性能较强.

表5 MTSFO-HIKMC在5类测试函数上的精度Tab.5 Accuracy of MTSFO-HIKMC on 5 types of test functions

5 结语

提出一种基于记忆传递旗鱼优化的K均值混合迭代聚类方法.首先通过最大最小距离积进行初始化KMC，然后利用自适应记忆传递修正策略改进SFO算法，提升了全局寻优能力和搜索精度，减少了由于SFO初始化误差较大造成的初始阶段多余的迭代次数，最后设计了MTSFO算法与KMC算法的混合迭代，提高了聚类精度，加快了收敛速度，应用价值明显.