海上直驱风电经柔直并网系统的次/超同步振荡特性分析
2023-01-03张志强李秋彤陈鸿琳孙海顺
张志强, 李秋彤, 余 浩, 陈鸿琳, 孙海顺
(1. 广东电网有限责任公司 电网规划研究中心,广州 510080;2. 华中科技大学 电气与电子工程学院,武汉 430074)
近年来,集群化、大容量、深远海成为海上风力发电(简称风电)发展趋势[1].随着离岸距离的增加,交流输电方式因为交流电缆充电无功功率过高而难以适用.柔性直流输电是基于全控型电力电子器件的新一代直流输电技术[2],已成为目前远距离海上风电并网的主要应用技术.直驱永磁风机因较高的效率、可靠性和良好的故障穿越性能,逐渐成为风电系统特别是海上风电的主流机型[3-4].在已投运或规划中的海上风电经柔直送出工程中,直流电压等级以±320 kV为主,风场规模多在500~1 100 MW 之间,直流海缆长86~205 km不等[5-6].
海上风电柔直输电系统通常包含多座海上风电场、柔直海上换流站以及陆上换流站,构成具有多个变流器控制的复杂系统,在实际运行中存在振荡失稳的风险.现已报道的振荡事故主要表现为两种形式,一种为风电机组与柔直送端变流器相互作用所致,如上海南汇、广东南澳的风电-柔直输电工程的次同步振荡[7-8];另一种则是柔直受端变流器与交流网络相互作用引发,如德国北海海上风电发生过的中高频振荡[8-10]以及舟山五端柔直、鲁西直流工程的高频振荡[7,11].这两种相互作用都对系统稳定运行构成严重威胁,因此有必要从并网系统整体建模的角度对风电经柔直并网系统的主导模态以及振荡场景进行研究.
风电经柔直并网系统的稳定性分析、振荡机理等问题已有相关研究成果报道,其中常用的分析方法包括阻抗法[12-13]和特征值法[14-15],也有相关研究从单输入单输出系统(Simple Input Simple Output, SISO)传递函数伯德图的角度开展小信号稳定性分析[16-17].针对风电场至柔直送端的稳定性问题,文献[14]采用特征值法分析风场与柔直送端系统间的振荡模态,指出风场至柔直送端变流器间存在场内及场网共两种次同步振荡模态,侧重研究两种模态的阻尼耦合趋势.文献[12-13]指出风场与柔直之间的振荡由风电机组及柔直变流器控制相互作用导致.文献[18]研究表明直驱风机控制器在次同步频率下呈现负电阻-电容特性,当与外部感性元件构成谐振电路且在阻尼不足时会发生次同步振荡.文献[12]和[16]分别基于风电机组网侧和柔直送端的dq阻抗和系统SISO传递函数,分析了风电机组和柔直变流器不同控制带宽对系统稳定性的影响.针对柔直受端变流器的稳定性问题,文献[17]采用与文献[16]类似的方法研究柔直受端锁相环与电流内环的带宽关系以及电网强度、有功功率对稳定性的影响.
以上文献多针对风场-柔直送端系统或柔直受端系统等局部系统的振荡模式和机理进行研究,缺乏对全系统动态特性及相互间耦合关系的认识;另外,基于现有的局部系统分析难以从全系统的角度考察振荡发生的原因及传播特性,厘清振荡发生的场景.对于多风电场经柔直并网系统,基于全系统状态空间建模的分析能够清晰地揭示全系统动态特性和主导振荡模态,明确与主导模态强相关的元件和控制环节以及控制参数和系统运行方式的影响;另一方面,振荡发生时会在全系统传播,通过全系统的特征值分析和时域仿真可以明确不同模式的振荡失稳在系统中的传播特性,从而厘清振荡的场景,指导控制参数和振荡抑制策略的设计.
基于上述考虑,本文以双直驱风场经柔性直流并网系统为例,通过建立全系统状态空间模型,首先明确全系统主导次/超同步振荡模态,揭示系统各主导模态的关联控制环节和关键参数,并进一步围绕主导模态研究控制参数和运行工况对其稳定性的影响,明确各主导模态的振荡在系统中的传播特性.所得结论对于认识多海上风电场经柔直并网系统动态特性及其控制设计具有指导意义.
1 研究算例介绍
图1给出了双海上直驱风电场经柔直并网系统结构图.两座容量各为500 MW的海上风电场由海上升压站升压后,经10 km的220 kV交流海缆连接到柔直海上换流站,柔直陆上换流站接入 500 kV 的交流主网架.柔直换流站容量为 1 000 MW,直流电压等级为±320 kV,直流海缆长90 km.图中:PCC1为公共连接点1;PCC2为公共连接点2.

图1 双直驱风场经柔性直流并网系统Fig.1 System of two direct-drive wind farms and VSC-HVDC
每座风场含90台5.5 MW永磁直驱型风电机组(Wind Turbine, WT),研究中认为同一风场内各机组的运行工况近似一致,采用单机倍乘的方式模拟整座风场.根据风电机组典型控制结构(见附录A)建立机组的全阶状态空间模型,所建立的模型涵盖机械-电气-控制等全部动态环节,包括风力机及桨距角控制、永磁发电机、机侧变流器及其控制(Machine Side Converter, MSC)、网侧变流器及其控制(Grid Side Converter, GSC)、锁相环控制等[19].
柔直输电系统送端变流器(Sending End Converter, SEC)采用恒频恒压控制方式为海上风电系统提供稳定的交流电压;受端变流器(Receiving End Converter, REC)控制直流电压恒定及送入交流系统的无功功率.同样,根据控制结构可建立其全阶状态空间模型.
联立图1中各元件的状态空间模型,消去中间代数变量,得到海上风电经柔直并网系统的全维状态空间数学模型,进而在给定运行点线性化后得到全系统小信号状态空间模型及状态矩阵[15,20].基于图1所示系统的线性化状态空间模型,研究海上风电经柔直并网系统的主导振荡模态.
2 系统特征模态与主导振荡模态
2.1 系统特征模态分析
考虑风电机组变流器和柔直换流器不同电流环控制参数下的4种工况,如表1所示.其中,工况一为系统典型运行方式,各变流器电流环控制参数均按照典型设计带宽200 Hz左右取值.相对工况一而言,工况二和三风电机组网侧电流环比例增益Kp5和Kp6递减,降低电流控制带宽,用于考察风电机组电流环控制参数的影响;工况四柔直受端电流环比例增益Kp12和Kp13降低,对应电流环带宽降低,用于考察柔直受端变流器电流环控制参数的影响.4种工况下风电场出力均按额定容量0.4(标幺值,p.u.)为基准设置,受端交流系统短路比(Short Circuit Ratio, SCR)设定为4,其余电气及控制参数详见附录B.

表1 工况设置Tab.1 Settings of working condition
在上述4种工况下分别计算全系统的特征值,其中位于次/超同步频段的特征值如表2所示,共对应有9对次同步振荡(Subsynchronous Oscillation, SSO)模态.通过参与因子分析,可以将这9对模态分为3类,分别对应风场-柔直模式、风场间模式和柔直-交流系统模式.其中,风场-柔直模式为海上风电机组与柔直送端变流器之间的控制相互作用主导,风场间模式为双风场之间的控制相互作用主导,柔直-交流系统模式为柔直受端变流器与陆上交流系统之间相互作用主导.
结合表1和表2可知,控制参数的变化会引起相关模态特征值的变化.分析表2中不同工况下特征值结果可见,工况一到工况三中,当改变风电机组网侧变流器电流环比例增益时,只有风场-柔直模式和风场间模式对应的特征值会发生变化,其中模态λ1, 2和模态λ3, 4的特征值实部由负变正,即对应模态由稳定变为不稳定状态,而与柔直-交流系统模式对应的3个特征值则一直保持不变,这是由于风场-柔直模式和风场间模式都与风电机组网侧电流环动态相关,而柔直-交流系统模式则基本与风电机组侧动态解耦.进一步对比工况一和工况四中特征值结果可见,当柔直受端变流器的控制参数发生变化时,只有柔直-交流系统模式会受到影响,其中λ5, 6的特征值实部由负变正,而风场-柔直模式及风场间模式所对应的特征值均保持不变,这说明由于柔直直流侧的解耦作用,柔直受端变流器动态特性的变化基本不会影响到风场侧特征模态的变化.从这种意义上来说,风场侧模式(包含风场-柔直模式与风场间模式)与柔直-交流系统模式之间是相互独立的.

表2 海上风电经柔直并网系统次/超同步频段特征模态Tab.2 SSO modes of offshore wind farm integrated system through VSC-HVDC
进一步根据表2中的特征值结果可知,海上风电经柔直送出系统在不同参数工况条件下,风场-柔直模式中的λ1,2、风场间模式中的λ3,4、柔直-交流系统模式中的λ5,6均可能出现特征值实部为正的情况,而其他模态的特征值实部在参数及运行工况变化时都始终保持为负,这表明模态λ1,2,λ3,4和λ5,6为所研究算例系统的主导振荡模态,需要重点关注.后续将主要针对此3对主导特征模态开展进一步分析.
2.2 主导模态参与因子分析
分别求取3对主导特征模态的归一化参与因子,结果如图2所示.海上风电经直流送出系统中状态变量的序号为0~106(风场A:1~22;风场B:23~44;升压汇集线路以及交流网络:45~78;柔直:79~106).参与程度较高的状态变量已于图中标注.图中:igd,igq分别为风电网侧电流d、q分量;igmq为风电网侧滤波后q轴电流;irq为柔直送端q轴电流;uimd,uimq为柔直受端d、q轴滤波后电压;z12,z13为柔直受端电流环状态变量;下标A、B表示风场A、B.
另一方面,分别计算特征模态λ1,2和λ3,4的右特征向量,将其中对应风场和柔直端口电流状态变量的元素画成图3所示的罗盘图,其幅值和相位表征了风场和柔直端口电流中,对应模态电流分量的相对大小和相位关系.
(1) 风场-柔直主导模态(λ1,2).
由图2(a)可知,在模态λ1,2中,两座风电场的网侧变流器及其控制部分、风场出口汇集线路、柔直送端变流器及其控制部分具有较高的参与程度,而柔直受端状态变量的参与程度均为0,说明主导模态λ1,2与柔直受端动态是解耦的.由图3(a)可知,两风场出口电流大小相等、方向相同,两者矢量和近似等于流入柔直送端的电流,说明该模态是两风场共同与柔直送端相互作用引起的,因此称其为风场-柔直主导模态.参与因子结果中风电机组网侧输出电流igd和igq、滤波后q轴电流igmq和柔直送端q轴电流irq参与程度明显高于其他状态变量的参与程度,表明风场-柔直主导振荡模态受风电机组网侧电流环控制参数、柔直送端电流环控制参数影响较大.

图2 各主导模态的参与因子Fig.2 Participation factors of dominant modes

图3 特征模式λ1, 2和λ3, 4右特征向量风场及柔直电流罗盘图Fig.3 Compass diagram of right eigenvector of λ1, 2 and λ3, 4 with respect to current of wind farm and VSC-HVDC
(2) 风场间主导模态(λ3,4).
由图2(b)可知,在模态λ3,4中,两座风电场的网侧变流器及其控制部分、风场出口汇集线路具有较高的参与程度,而其他状态变量的参与程度均为0,表明主导模态λ3,4与柔直送端变流器及受端系统动态是解耦的.由图3(b)可知,两风场出口电流大小相等、方向相反,而流入柔直送端电流为0,说明该模态是由两风场之间相互作用引起的,因此称其为风场间主导模态.参与因子结果中,风电机组网侧输出电流igd和igq以及滤波后q轴电流igmq参与程度明显高于其他状态变量的参与程度,表明该模态受风场网侧变流器电流环控制参数影响较大.
(3) 柔直-交流系统主导模态(λ5,6).
由图2(c)可知,在主导模态λ5,6中,仅柔直受端变流器及其控制部分和陆上等效交流网络部分具有较高的参与程度,而柔直送端变流器部分及海上风电场部分的参与程度为0,表明该主导模态与海上风电场侧动态环节是解耦的,λ5,6是柔直受端变流器与交流电网相互作用的结果,因此称其为柔直-交流系统主导模态.参与因子分析结果表明,受端电流环状态变量z12和z13参与程度较高,说明柔直-交流系统主导模态受柔直受端变流器电流环控制参数影响较大.
以上分析表明,多海上风电场柔直并网系统存在3种主导次/超同步模态,分别为风场-柔直主导模态、风场间主导模态以及柔直-交流系统主导模态,其中风场-柔直主导模态和风场间主导模态对应系统海上多变流器之间的控制相互作用,柔直-交流系统主导模态对应柔直变流器与交流电网之间的相互作用,两种相互作用相互解耦.
3 系统主导模态关键影响因素与失稳场景分析
参与因子分析表明,海上风电经柔直并网系统上述3种主导模态均与相应的变流器电流控制强相关,以下重点研究控制变流器电流控制参数和运行工况对各模态稳定性的影响,明确各主导模态失稳场景及其在系统中的传播特性.
3.1 风场-柔直主导振荡模态的关键影响因素和失稳场景
(1) 风电机组网侧变流器电流环控制参数影响.
保持表1内工况一中其他参数不变,分别改变风电网侧变流器电流环比例增益(由1.6减小至0.3,带宽由274 Hz减小至52 Hz)和积分增益(由20增大至170,带宽由200 Hz增大至 202 Hz),计算得到风场-柔直主导模态的根轨迹如图4所示.
由图4(a)可知,随着电流环比例增益降低,电流环控制回路带宽有所增加,风场-柔直主导模态在复平面内向右移动,模态阻尼逐渐减弱,稳定性降低;同时由于电流环带宽减小,模态频率减小.由图4(b)可知,积分增益的增加也会使得模态阻尼趋于减弱,稳定性降低;但是由于积分增益几乎不改变电流环带宽,所以模态频率几乎不变.可见,风场-柔直主导模态频率变化与风电网侧变流器电流控制回路带宽变化密切相关,其阻尼特性则同时受电流环比例增益和积分增益影响.
(2) 柔直送端变流器电流环控制参数影响.
保持表1内工况一中其他参数不变,分别改变柔直送端变流器电流环比例增益(由1减小至0.1,带宽由260 Hz减小至62 Hz)和柔直送端变流器电流环积分增益(由30增大至140,带宽由224 Hz增加至225 Hz),计算得到风场-柔直模态的根轨迹如图5所示.结果表明,柔直变流器电流比例增益降低也会导致风场-柔直主导模态趋于失稳,但是对模态频率的影响较小,只是略有降低;另一方面,柔直变流器电流环积分增益增大,使得风场-柔直主导模态向右移动,趋于不稳定.

图5 风场-柔直主导模态随SEC电流环控制参数变化的根轨迹Fig.5 Root locus of dominant mode of wind farms and VSC-HVDC with changes of control parameter of SEC current loop
对比上述分析可以发现,风场-柔直主导模态稳定性同时受风电和柔直变流器电流环控制参数的影响,而模态频率主要受风电变流器电流控制比例系数的影响.
(3) 运行状态的影响.
风电并网系统振荡模态除了受变流器控制参数影响外,还受到风电场出力等运行状态的影响.分别针对表1工况一、二、三,将风场出力由0.8(p.u.)逐渐降低至0.1(p.u.),得到3种工况下风场-柔直主导模态随风电出力变化的根轨迹,如图6所示.可以发现,风电出力越低,风场-柔直主导模态阻尼越弱,同时模态频率略有降低;对比工况一、二、三可知,风电变流器电流环比例增益越低(工况二、三),能够保证模态稳定性的风电出力范围越窄.另外,由于柔直送端与受端模态相互解耦并且受端短路比不影响送端潮流,所以陆上交流系统短路比的变化不会对风场-柔直主导振荡模态稳定性造成影响.

图6 风机出力变化对应的风场-柔直主导模态根轨迹Fig.6 Root locus of dominant mode of wind farms and VSC-HVDC with changes of output of WTs
以上分析表明,风场-柔直主导模态的阻尼与风电和柔直变流器电流环控制以及风场出力密切相关,风场低出力、风电以及柔直变流器电流环比例增益降低或是积分增益增大,均会导致风场-柔直主导模态阻尼减弱;另外模态频率主要受风电网侧变流器电流环比例系数的影响.
(4) 时域仿真分析.
在PSCAD/EMTDC中建立算例系统的详细电磁暂态仿真模型,以工况一为初始条件建立稳态,随后在3 s时降低风电机组网侧电流环比例系数,系统切换至工况二状态,风场-柔直主导模态失稳,分别记录风场A出口有功功率(PA)和柔直受端并网点处有功功率(PPCC2)波形,如图7所示.可见,改变风电电流环控制参数后,风场输出的有功功率出现发散振荡,振荡频率为48.65 Hz,与表2特征模式分析结果48.39 Hz基本一致.

图7 风场A出口及PCC2有功波形Fig.7 Active power at outlet of wind farm A and PCC2
在柔直受端并网点PCC2处,有功功率也呈现出频率(49.02 Hz)非常接近风电振荡的振荡现象.由表2特征值可知,该工况下柔直-交流系统模态为稳定模态,且模态频率为26.94 Hz.可见风场-柔直主导模态失稳时,振荡会传递到柔直受端,柔直受端与交流系统侧表现为受迫振荡而非特征模式失稳.仿真中在6 s时将系统状态切换回工况一后,柔直送端与受端振荡均平息,系统恢复稳定.
3.2 风场间主导振荡模态分析
(1) 风电机组网侧变流器电流环控制参数影响.
在工况一所列参数条件下,风电机组网侧变流器电流环比例增益由1.6降低至0.3,带宽由274 Hz降低至52 Hz;积分增益由20增大到170,带宽由200 Hz增加至202 Hz,变化过程中风场间主导振荡模态的根轨迹如图8所示.可见,随着比例增益的降低、积分增益的增大,风场间主导模态阻尼减弱,模态特征值可能进入右半平面,表明风场间主导模态存在振荡失稳的风险;同时由于比例增益和积分增益与电流环带宽的关系,随着比例增益的增大,风场间主导模态频率有所降低;而积分增益的改变则几乎不影响风场间主导模态的频率.
对比分析图4(a)和图8(a)可知,同样的参数条件下,风场间主导模态的实部始终小于风场-柔直主导模态的实部,即风场-柔直主导模态会先于风场间主导模态穿过虚轴进入右半平面,说明在研究场景下,当风场间主导模态失稳时,会同时伴随风场-柔直主导模态的振荡.

图8 风场间主导模态随GSC电流环控制参数变化的根轨迹Fig.8 Root locus of dominant mode of wind farms with changes of control parameter of GSC current loop
(2) 运行状态的影响.
在工况一~三中将风电机组出力由0.8(p.u.)逐渐降低至0.1(p.u.),得到不同工况下风场间主导模态的根轨迹,结果如图9所示.可知,随着风电机组出力的降低,风场间主导模态在复平面内向右移动,模态频率略有降低.对应工况三的风电变流器控制参数,在一定的出力水平风场间模态会发生振荡失稳,在工况一和工况二的风电变流器控制参数条件下该模态始终保持稳定,说明风电变流器电流环控制参数对该模式稳定性具有重要影响.

图9 风机出力变化对应的风场间主导模态根轨迹Fig.9 Root locus of dominant mode of wind farms with changes of output of WTs
以上分析表明,风场间主导模态阻尼与风场机组网侧变流器电流控制参数密切相关,风场出力对稳定性有一定的影响,表现为风电机组电流环比例增益较小、积分增益较大、低出力下该模态容易失稳.模态频率受风电变流器电流环比例增益影响较大.柔直送端变流器控制对该模态没有影响,风场间主导模态失稳可能伴随风场-柔直主导模态振荡.
(3) 时域仿真分析.
在时域仿真中以工况一建立稳态,随后在3 s时改变风电机组网侧控制器电流环比例增益,使系统切换至表1中工况三状态,根据特征值分析,此时系统中应同时存在风场-柔直主导模态和风场间主导模态的振荡失稳.
两风场输出的有功功率之差(Pd)可以反映风场间主导模态振荡,对应两风场之间的功率环流,不会进入到柔直侧,仿真结果如图10(a)所示.当系统切换到工况三后,风场间主导模态失稳,对应振荡频率约为38.94 Hz,与表2计算模态频率39.77 Hz基本相符.
公共连接点PCC1点送往柔直变流器的有功功率(PPCC1)反映风场-柔直主导模态,表现为两风场共同对柔直变流器的振荡,仿真结果如图10(b)所示.

图10 两风场有功差值波形及PCC1点有功Fig.10 Active power difference of two wind farms and PCC1
可以看到风场-柔直主导模态也发生振荡,发散振荡频率与计算结果38.32 Hz基本相符.
上述分析表明,多海上风电场经柔直并网系统中,可能同时存在风场-柔直主导模态和风场间主导模态的稳定性问题,与风电场机组网侧变流器电流控制参数设计有关,在风场低出力时更易失稳.
3.3 柔直-交流系统主导振荡模态分析
(1) 柔直受端变流器电流环控制参数影响.
参与因子的分析表明,柔直-交流系统主导模态受柔直受端变流器电流环控制参数的影响较大.在表1中工况一的条件下,保持其他参数不变,分别降低柔直受端变流器电流环的比例增益,由1.05减小至0.3,带宽由310 Hz降低至144 Hz,并增加积分增益,由20增加至240,带宽由266 Hz增加至 267 Hz,得到柔直-交流系统主导模态的根轨迹,如图11所示.结果表明,柔直-交流系统主导模态频率随着比例增益降低出现先增加后降低的变化趋势,随着积分增益增大振荡频率持续增加;另一方面,比例增益降低或积分增益增大后,柔直-交流系统主导模态在特征根平面上向右移动,表现为阻尼特性减弱,直至进入右半区模态失稳.
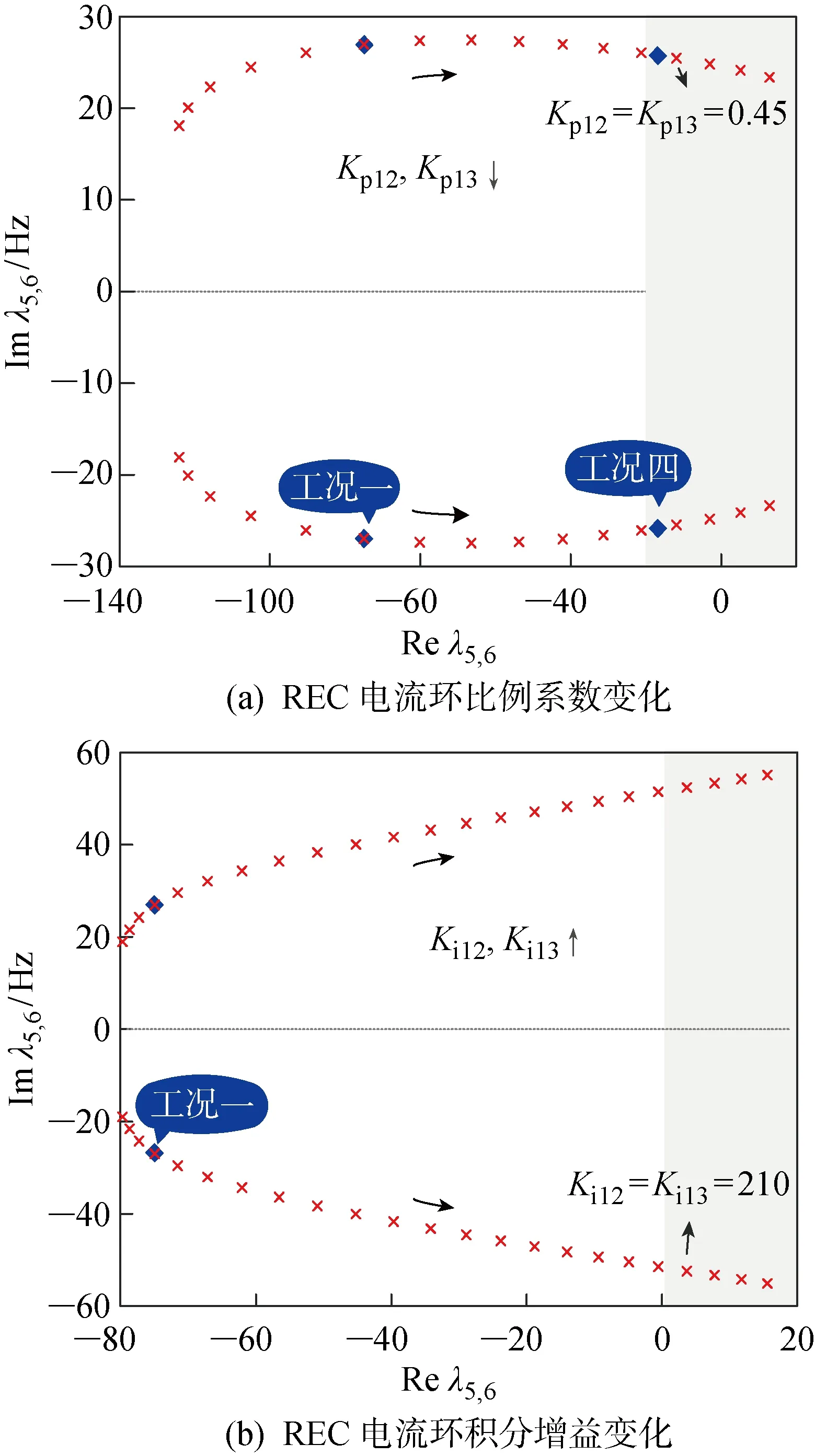
图11 柔直-交流系统主导模态随REC电流环控制参数变化的根轨迹 Fig.11 Root locus of dominant mode of wind farms with changes of AC grid control parameter of REC current loop
(2) 运行状态的影响.
考虑交流系统短路比对柔直-交流系统主导模态稳定性的影响.分别针对工况一和工况四,将交流系统短路比由5逐渐降低至1.2,得到不同工况下柔直-交流系统模态根轨迹,如图12所示.结果表明,交流系统短路比对柔直-交流系统主导模态的振荡频率和稳定性具有明显影响,随着短路比的减小,柔直-交流系统主导模态阻尼减弱,稳定性降低.对比工况一与工况四,由于控制参数取值不同,保持模态稳定的临界短路比有很大区别.
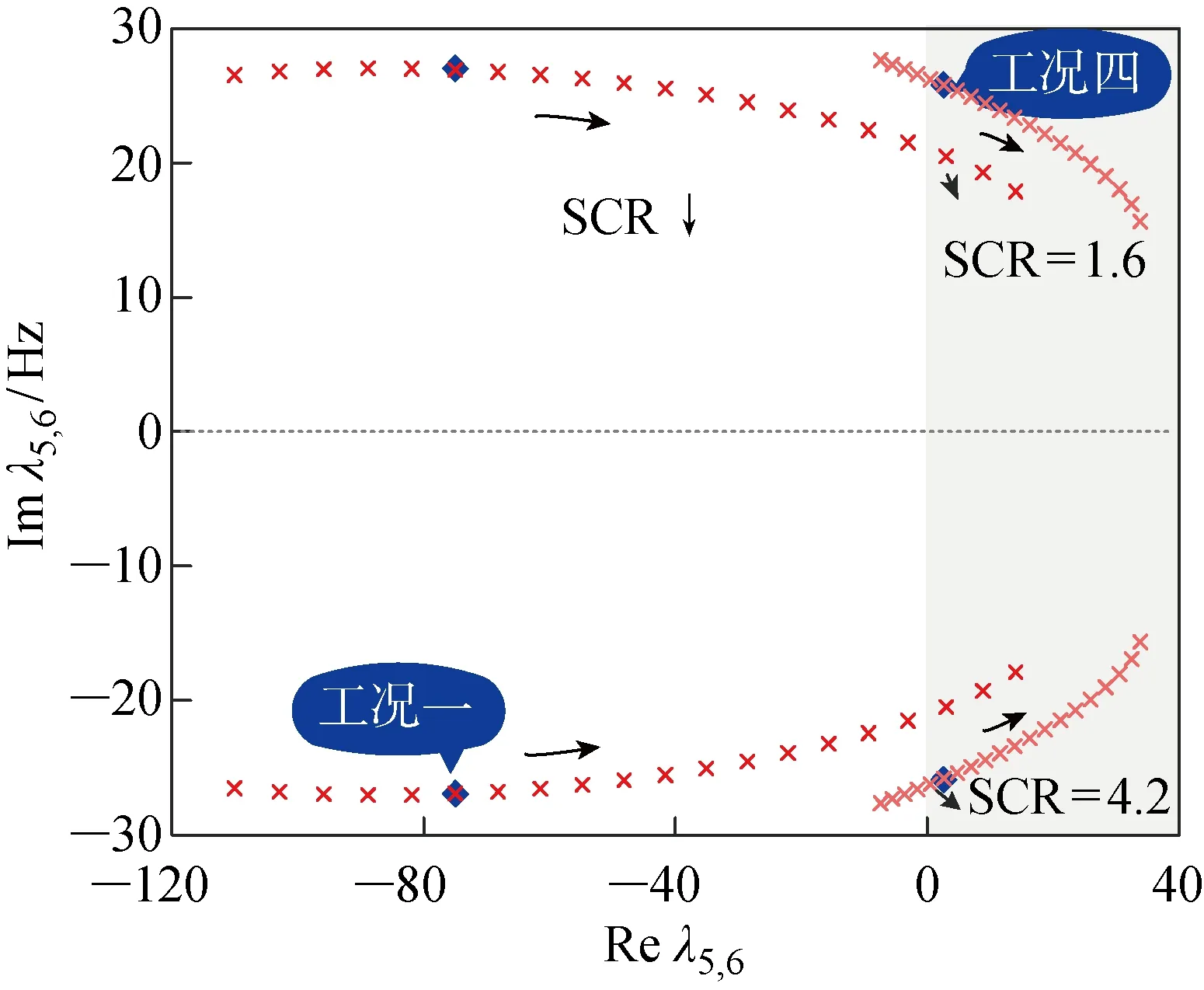
图12 SCR变化对应的柔直-交流系统主导模态根轨迹Fig.12 Root locus of dominant mode of wind farms and AC grid with changes of SCR
基于表1中工况一参数,分别考虑两种交流系统短路比SCR=1.7,2.5,逐渐将系统传输的有功功率由0.65(p.u.)减小至0.1(p.u.),对应的模态特征根轨迹如图13所示.当受端短路比为2.5时,风机出力的降低并不会导致模态失去稳定;而当受端短路比为1.7时,柔直交流系统主导模态在系统传输有功出力降低到0.35(p.u.)时就已经失稳,表明交流系统短路比对该模态稳定性具有重要影响.

图13 传输有功功率变化对应的柔直-交流系统主导模态根轨迹Fig.13 Root locus of dominant mode of wind farms and AC grid with changes of active power
以上分析表明,柔直-交流系统主导模态表现为柔直变流器与交流系统之间的相互作用,其模态频率和稳定性与柔直受端变流器电流环比例增益和积分增益密切相关,交流系统短路比对该模态频率和稳定性也有重要影响.
(3) 时域仿真分析.
基于图1所示系统的详细电磁暂态模型,以表1的工况一为初始条件建立稳态,随后在3 s时降低柔直受端变流器电流环比例增益,使得系统换至工况四状态,柔直-交流电网主导振荡模态失稳,记录柔直受端并网点PCC2的有功功率波形,如图14所示.可见,工况变化之后,柔直并网点PCC2处的有功功率开始振荡发散,对应起振频率为26.68 Hz,与表2分析结果25.81 Hz基本相符.

图14 风场A及PCC2有功波形Fig.14 Active Power at outlet of wind farm A and PCC2
另一方面,风场输出的有功功率也出现与柔直受端同频率的振荡,振荡幅值相对小于柔直受端,振荡频率不同于风场柔直主导模态和风场间主导模态,这是由于柔直受端的振荡传播到风场一侧导致的受迫振荡.表2特征值结果也表明此时风场-柔直主导模态和风场间主导模态均保持稳定.在仿真的第6 s将系统状态切换回工况一后,柔直受端与送端均恢复稳定.
4 结论
以海上风电场经柔直输电并网系统为例,分别建立全系统状态空间数学模型和详细电磁暂态仿真模型,通过特征模式分析和时域仿真研究系统主导振荡模态,结果表明:
(1) 多海上风电场柔直并网系统存在3种主导次/超同步振荡模式,分别为风场-柔直主导模态、风场间主导模态以及柔直-交流系统主导模态,其中风场-柔直主导模态和风场间主导模态对应系统海上多变流器之间的控制相互作用,柔直-交流系统主导模态对应柔直变流器与交流电网之间的控制相互作用,两种控制相互作用相互解耦.
(2) 风场-柔直主导模态的稳定性主要受风场机组网侧和柔直送端变流器电流控制以及运行工况的影响较大;风场间主导模态稳定性与风场机组网侧变流器电流控制以及运行工况密切相关,而柔直换流器控制对其没有影响.分析表明,一定范围内变流器电流环比例增益越小、积分增益越大、风场出力越低,两种主导模态越容易失稳,稳定临界出力与控制参数有关;风场间主导模态失稳常伴随风场-柔直主导模态失稳.
(3) 柔直-交流系统主导模态稳定性主要与柔直受端变流器电流环控制参数和系统运行状态有关,表现为柔直变流器电流环比例增益较小、积分增益较大、风机低出力和低短路比时系统容易失稳,稳定临界出力与给定控制参数和交流系统短路比有关.
(4) 风场-柔直主导模态失稳时振荡会传播到柔直受端与交流电网侧,同样柔直-交流系统主导模态的失稳也会引起风场与柔直海上换流站的振荡.通过全系统状态空间建模分析可以清晰地揭示振荡发生的根源和主要关联环节,有利于开展针对性的振荡抑制策略设计.
本文通过全系统状态空间分析,对多海上风电场经柔直并网系统的次超同步振荡特性以及3种主导次/超同步振荡模态的特性和关键影响因素进行研究.在此基础上,未来将通过特征值灵敏度分析深入研究变流器不同时间尺度控制环节对3种主导振荡模态稳定性的影响,以及在风电全出力范围保持3种主导振荡模态稳定的各变流器控制参数取值范围等.
附录见本刊网络版(xuebao.sjtu.edu.cn/article/2022/1006-2467-56-12-1572.shtml)
