星座碰撞规避的迭代学习构型保持方法
2023-01-03陶昊宸龙嘉腾朱圣英
陶昊宸,龙嘉腾,朱圣英,聂 涛
(1. 北京理工大学宇航学院,北京 100081;2. 深空自主导航与控制工信部重点实验室,北京 100081;3. 飞行器动力学与控制教育部重点实验室,北京 100081)
0 引言
巨型低轨卫星星座的开发,已成为当下的热点领域,但巨型星座快速发展的同时也存在一系列问题,其中最直接的后果是造成了500~2000km范围近地空间的异常拥挤[1-3]。随着低轨卫星数量的急剧增加,一方面使已有在轨卫星的生存空间受到挤压,碰撞风险增大;另一方面,发射和轨道机动等工作的负担和风险也与日俱增,严重时甚至会引发碎片级联碰撞效应等灾难性后果,对空间环境造成极大破坏[4-6]。
为了保证空间目标的安全运行,碰撞规避方法的研究受到了广泛关注[7-9]。通常碰撞规避问题可以描述为:卫星在得到预警信号与相对运动关系等信息后,如何机动降低碰撞概率。对于推力矢量控制的卫星,问题转化为约束条件下的最优脉冲输入的求解。R.P.Patera等[10]最早研究了相关问题,将推力方向与大小解耦,开发了一种基于碰撞概率梯度的规避策略,沿碰撞概率梯度方向进行轨道机动,使碰撞概率以最快速度下降。此后的研究基本沿着该思路展开,例如安喜彬等[11]考虑了卫星回归原轨道、燃料最省和距离下限的约束条件,使用高斯伪谱法求解最优控制规律。袁勇等[12]采用了时间规避策略,在碰撞前施加沿速度方向的脉冲,使两星通过轨道面交点的时刻错开,从而避免相撞。
随着电推进技术的飞速发展,越来越多的卫星使用连续低推力方法进行轨道控制。相比推力矢量控制,这种方法能大幅提高控制效率,从而延长卫星的使用寿命。然而,基于连续推力控制的规避方法却鲜有研究。G.Salemme等[13]提出了一种间接方法,以燃料最省为优化目标,但模型维度较高。J.Herna-ndo-Ayuso等[14]在此基础上,以推力最小为目标,基于Pontryagin极大化原理与间接法,分别对连续推力的幅值与方向求最优,研究了圆轨道两星碰撞规避问题,并推导了精度较高的切向机动解析解。J.A.Reiter等[15]基于最优推力径向假设,提出了一种半解析快速计算方法。目前,连续推力控制方式在大型低轨道互联网星座领域已取得广泛应用[16-17],因此本文的研究也将基于连续推力控制展开。
在星座卫星的巨大规模下,碰撞规避将成为常规任务[7]。因此,为了避免过度机动造成的次生碰撞和燃料浪费,应在尽可能减小对任务造成影响的前提下,提出更便捷的规避策略,便于卫星在轨执行。目前星座卫星的研究中,更多的是将避碰作为一项约束,讨论构型保持的问题[18-19]。冯昊等[20]在设计遥感卫星空间碎片规避机动策略时,以星下点轨迹允许范围为约束,在环形区域内实行精确控制,以达到规避效果。受星座构型保持启发,考虑到决定两星碰撞风险的众多要素中,距离的影响最为重大[21-23]。本文提出了一种基于相对轨道保持的碰撞规避方法,将复杂的规避寻优问题转化为轨道控制问题,通过精确控制减少不必要的机动,这也有益于卫星的正常任务。
相对轨道保持的核心问题在于相对摄动建模,对于近地卫星,地球形状摄动是主要摄动源[24-25]。由于互联网星座卫星以近圆轨道为主,容易产生碰撞风险的卫星轨道高度相当,因此运行周期也十分接近,加之地球非球形引力摄动又呈现出明显的周期性,这就导致了相对运动模型中的复杂摄动项以周期重复为主。一般的反馈控制可以抑制非周期误差,但并不能有效地消除周期性摄动引起的周期误差,与理想的相对轨道始终存在偏差,控制效果不理想[26-27]。迭代学习控制(Iterative Learning Control, ILC)是一种通过重复控制轨迹修正控制律的方法,最早由S.Arimito[28]提出,用于提高机器人轨迹跟踪精度。由于其控制输入由先前试验得到,不依赖于精确模型,因此被广泛引入其他领域。
针对周期性为主的复杂相对摄动,本文提出了基于ILC的星座卫星碰撞规避与构型保持方法。首先,对地球形状J2摄动进行建模,使用轨道模型作差的方法得到相对运动模型;其次,以相对距离为控制目标引入反馈控制,跟踪相对轨道;在此基础上,基于相对摄动周期构建ILC控制器,提取轨道保持偏差与控制输入,生成下一周期的输入,从而抵消周期性扰动的影响,提高轨道保持精度,以不同轨道倾角的圆轨道近地卫星为例进行了数值仿真。
1 动力学建模
首先定义轨道坐标系,原点O位于目标航天器或卫星的质心,Ox轴(R轴)指向目标矢径方向,Oy轴(S轴)在轨道平面内与Ox轴垂直,指向目标速度方向,Oz(W轴)与轨道平面垂直,与Ox、Oy轴构成右手坐标系,称为RSW坐标系。其中,W轴方向与目标比角动量h方向一致,但S轴并不一定与速度矢量重合。
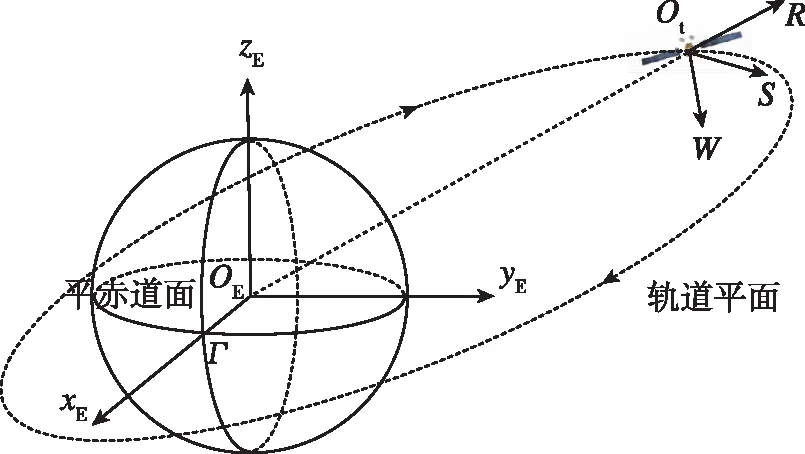
图1 地心惯性系(ECI)与轨道坐标系(RSW)关系图Fig.1 Relation between earth centered inertial frame and orbit frame
设威胁星在目标星RSW系中的相对位置为 (x,y,z)T,则有
(1)
式中,下标t与d分别表示目标星和威胁星;ρ为两星相对位置矢量;f为目标星真近点角。
由于近地卫星的主要摄动源是地球扁率,因此仅显化2阶带谐项摄动,其在地心惯性坐标系(Earth Centered Inertial,ECI)下可表示为
(2)
进行坐标转换并代入二体运动方程,可得目标星RSW系下的相对运动方程为
(3)
式中,ap=[apx,apy,apz]T表示轨道系下的相对摄动加速度;as=[asx,asy,asz]T表示其他未建模的非周期扰动以及近似误差;ac=[acx,acy,acz]T表示三轴的控制分量。
由于有碰撞风险的两近圆轨道卫星轨道高度近似相等,即rt≈rd,方程可简化为
(4)
式(4)即为卫星相对加速度描述,包含摄动的相对运动动力学模型的矩阵形式为
(5)
式中
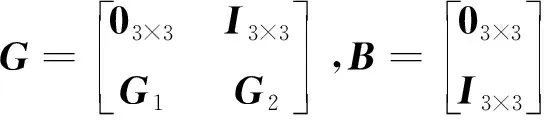
(6)
2 星座碰撞规避的迭代学习构型保持方法
相对轨道保持首先需要选定理想的相对轨道,本文以不受摄的二体运动轨道为卫星的理想轨道,并得到理想相对轨道,以下标q表示。状态变量为xq=[rqvq]T。
相对轨道保持的过程,实际上是通过控制输入,消除或稳定相对距离跟踪偏差的过程。设T为ILC控制周期,控制输入包含两部分——反馈项afb与ILC项aILC,总控制输入为二者加和ac=afb+aILC。定义相对轨道保持偏差
(7)
因此,有偏差状态变量e=[erev]T。
令合扰动ah=ap+as,由于地球形状与太阳光压等摄动加速度均为卫星位置矢量的函数,可用r表示扰动上界
(8)
因此,根据三角不等式,相对摄动的上界也可用相对距离矢量表示

(9)
式中
(10)
根据式(9),非周期摄动与偏差状态矢量的模也存在如下关系
(11)
式中
(12)
2.1 反馈保持控制器设计
针对相对摄动建模误差与未建模摄动的非周期影响,引入反馈保持控制器跟踪理想相对轨道,并稳定轨道保持偏差。下面给出反馈保持器的增益设计方法。
卫星相对动力学模型式(5)中,相对加速度的描述为
(13)
设计反馈控制输入afb为
(14)
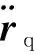
(15)
容易验证在式(14)反馈控制输入下系统的稳定性和偏差的有界性。
2.2 ILC保持控制器设计
在2.1节中,通过引入反馈控制器,抑制了非周期摄动下相对轨道保持偏差的发散。针对主要摄动项ap,本节将设计ILC保持器,进一步抵消周期变化的保持偏差,实现稳定的相对轨道保持。
理想相对轨道加速度描述为
(16)
与式(13)相减得到偏差加速度描述
(17)
在式(17)中加入速度偏差描述式,写成偏差状态方程
(18)
设计ILC保持器时,控制输入ac=aILC,式(18)可写作
(19)
ILC保持器输入的确定依赖于前一周期的保持偏差和ILC输入信号,使用分段函数进行表示[29]
aILC(t)=
(20)
式中,L为ILC增益矩阵,且有
(21)
增益系数κr、κv由保持偏差决定,本文采用双曲正切函数定义
(22)
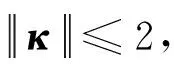
(23)
下面判断系统稳定性,并计算ILC保持偏差收敛半径。
设实对称矩阵P2正定,满足
ATP2+P2A=-p2I6×6
(24)
式中,p2>0。以关于e的二次型函数为Lyapunov函数
V2(t)=eT(t)·P2·e(t)
(25)
两边求导并代入式(19),得到
(26)
代入扰动上限式(11)与ILC输入表达式(20),得
(27)
根据当前与上一周期偏差e的关系
(28)
代入式(19)得
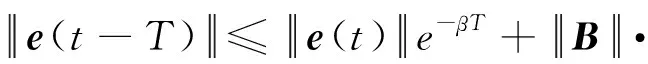
(29)
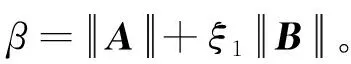
(30)
在一个周期内,定义最大控制输入大小
(31)
代入式(30),并利用矩阵次可加性展开得
(32)
合并、化简得
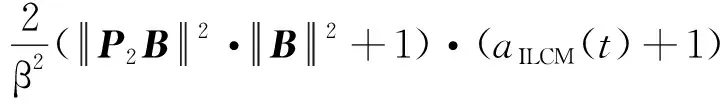
(33)
在式(33)中,令
(34)
则
(35)
设P2的特征值中最大者为λ2M,最小者为λ2m,则V2满足
(36)
ζ1>0时,将式(36)代入式(35),得
(37)
求解得
(38)
再次利用式(36)关系,式(38)可进一步化为
(39)
两边取平方根得
(40)
在式(40)中,令
(41)
则
(42)
再令时间t→∞,有
(43)
当υ1<1时,有
(44)
式(44)表明,在ILC控制输入式(20)的作用下,相对轨道保持偏差将收敛到0的邻域,收敛半径为R2c。
值得一提的是,在υ1以及R2c的表达式中并未涉及偏差初值,因此本章所设计的ILC保持器的收敛特性与初始偏差无关。这是由于式(20)在生成每个周期的控制输入时,偏差初值都被纳入考量。这种初值无关特性意味着在实际应用中,可以依约束启动ILC保持器,相对轨道保持偏差最终都能得到有效控制。
3 数值仿真与分析
卫星星座往往采用同轨道高度、多组轨道倾角卫星组网的部署模式,因此本章将模拟此类情况开展分析研究。设存在如图2所示的两颗近圆轨道卫星,初始时刻轨道根数如表1所示,轨道高度非常接近,周期仅相差1.2s。
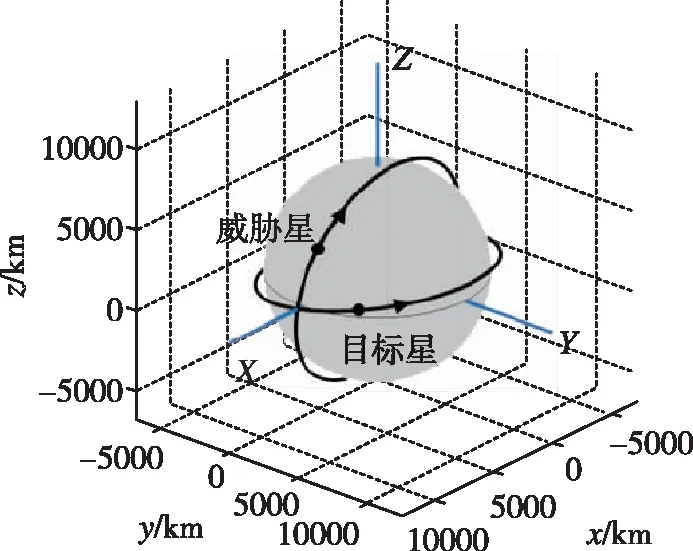
图2 两星理想轨道示意图Fig.2 Ideal orbits of two satellites

表1 两星轨道根数
在理想情况下,目标星轨道坐标系中的相对轨道如图3所示,类似于一个弯曲的“8”字型。但在地球形状摄动的影响下,相对轨道会逐渐偏离理想值,如图4所示。这种偏差是发散的,在完全不进行绝对轨道保持的情况下,2.5h后距离发散至61.395km,可能引发两星最近距离的减小,这正是造成卫星碰撞的关键原因。
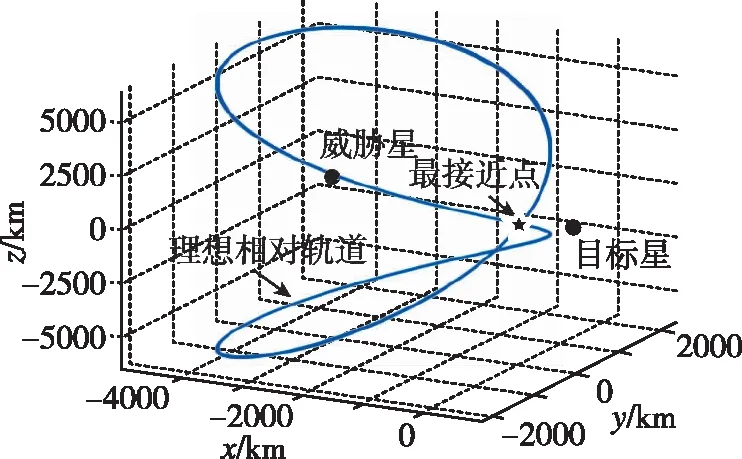
图3 三维理想相对轨道图Fig.3 Ideal relative orbit

(a) R向
两星在摄动影响下的相对距离变化如图5所示,偏差相较于相对轨道而言很小,但在8037s左右,两星达到第二周期内的最接近时刻,此时实际相对距离ρ已降至2.069km,产生了一定的碰撞风险[30],图6直观地给出了两星实际位置关系与理想情况的对比。
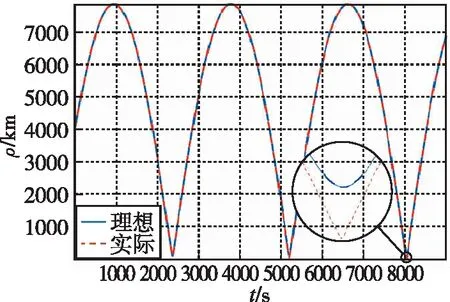
图5 两星距离变化曲线(2.5h)Fig.5 Change of the distance between two satellites (2.5h)
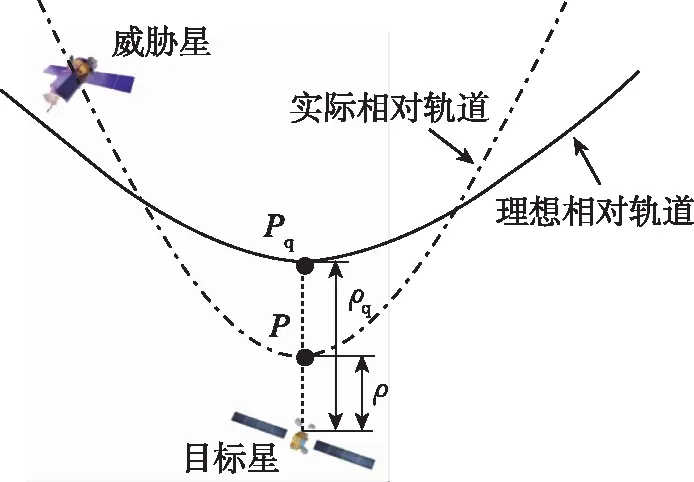
图6 摄动影响下最接近距离变化示意图Fig.6 Distance of closest approach under perturbation
选择ILC控制周期为相对摄动周期5676s,分别对系统施加反馈控制与ILC+反馈控制方式,图7给出了两星相对位置、相对速度与理想值的偏差er、ev的三轴分量变化情况。
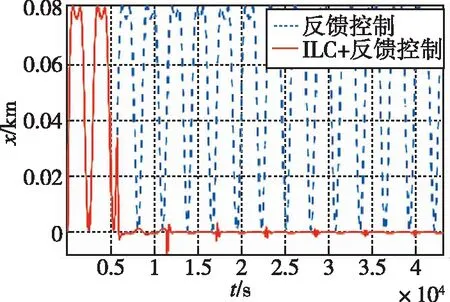
(a) R向位置
在仅有反馈控制的情况下,位置与速度偏差均会保持振荡,其中碰撞分析更关注的是位置偏差er、er三轴分量的振幅分别达到了80.2m、34.4m和79.2m。而在ILC+反馈控制下,这种振荡在第二周期就已经有了明显的削弱,并在两个周期后被基本消除。
图8给出了位置偏差的模er的变化情况,仅反馈控制作用下,距离偏差的振幅为109.7m,使用本文提出的ILC反馈控制,三个周期后最大偏差不超过5m。同时结合图7可知,ILC反馈控制偏差仅在新周期学习开始时快速波动,耗时约10min,而在剩下的约85min内,距离偏差er均保持在1m以内。表2给出了每个控制周期开始时的最大距离偏差。
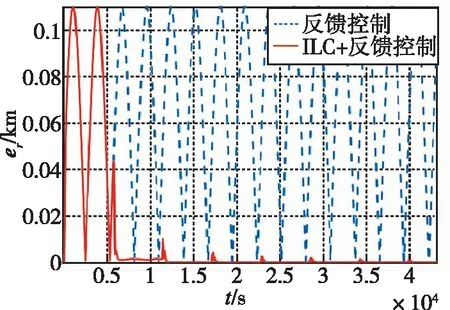
图8 两种控制方式距离偏差er对比图(12h)Fig.8 Comparison of er by two control methods (12h)
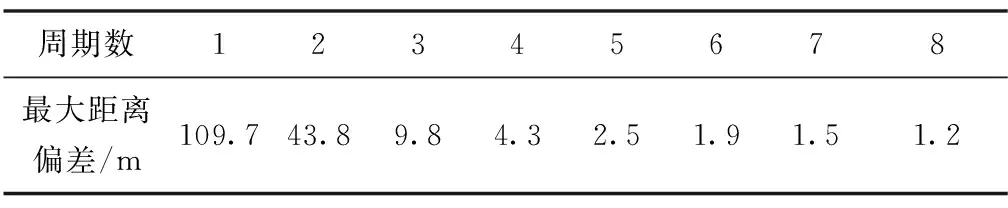
表2 ILC周期起始段最大距离偏差
图9给出了反馈控制作用下,ILC控制器启动时间不同时,距离偏差er的收敛情况,验证了本章设计的ILC保持器偏差收敛性与初始条件无关的特性。因此,在实际应用中,可以根据碰撞预警信息和其他约束条件灵活选择ILC保持器启动时间。
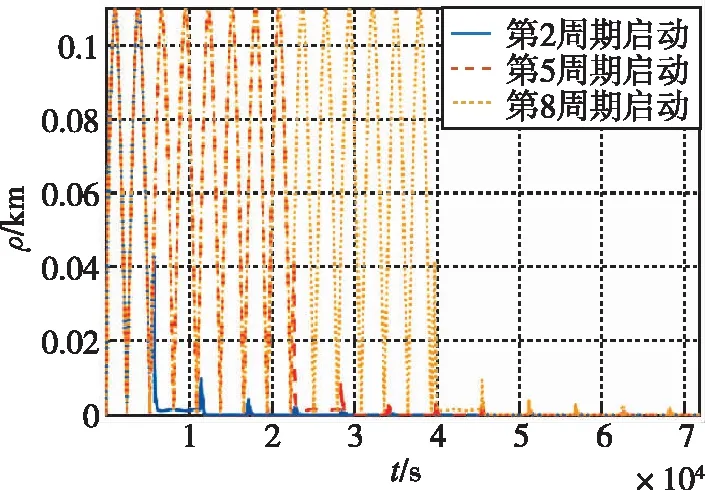
(a) 不同周期
将控制输入ac与扰动ap作差,得到输入的跟踪误差
δa=ac-ap
(45)
图10给出了δa的三轴分量变化情况,反映了两种控制方式对扰动ap的跟踪效果。明显地,反馈控制无法消除周期性的跟踪误差,而ILC反馈控制输入在每个控制周期开始时浮动较大,但大部分时间跟踪能力远胜于反馈控制。控制输入量级与摄动项相当,因此不存在控制输入过大、超出机动能力范围或损坏星上设备的问题。
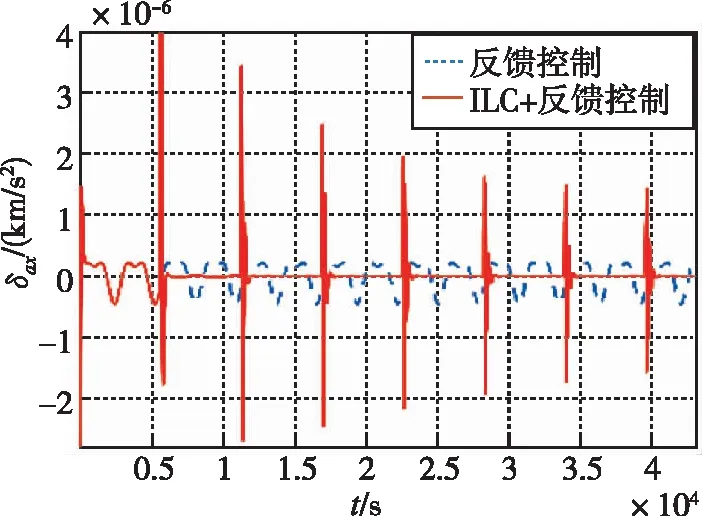
(a) R向
图11在图5的基础上,添加了本文ILC反馈控制方法作用下的距离曲线。加入控制后,最接近时刻附近的实际相对距离与理想轨道基本一致,实际最接近距离大于75km,碰撞概率低于10-10,可直接排除碰撞可能,因此达到了规避碰撞的目的。
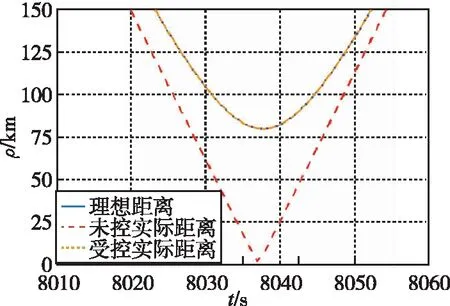
图11 相对距离保持效果图Fig.11 Effect of distance keeping
需要指出的是,在本例中两星理想接近距离在75km以上,因此两种控制方法的偏差都可保证相对距离足够远,不会发生碰撞。但在理想最近距离仅有数千米或更短时,相较于反馈控制百米级的精度,ILC反馈控制米级的跟踪精度具有明显的优势。
4 结论
本文针对圆轨道卫星间的碰撞问题,提出了一种普遍可行的规避机动方法,选定理想相对轨道,通过高精度的构型保持降低碰撞风险。本文得到结论如下:
1)针对J2项影响为主的相对摄动变化情况,在传统反馈控制的基础上,通过ILC方法实现控制输入对周期性摄动的精确跟踪。
2)ILC控制器的收敛半径与初始条件无关,可以依据约束条件在任意相对运动状态下启控,具有启控时间灵活选择和快速收敛的优点。
星座间的碰撞问题均可通过构型保持的方法解决,本文提出的ILC仅是对无约束圆轨道卫星的初步应用。未来,应针对具体卫星,引入具体约束,研究变周期ILC问题,并将方法推广到椭圆轨道情形。
