基于深度Q网络的多智能体逃逸算法设计
2023-01-03闫博为杜润乐班晓军
闫博为,杜润乐,班晓军,周 荻
(1. 哈尔滨工业大学航天学院,哈尔滨 150000;2. 试验物理与计算数学国家级重点实验室,北京 100076)
0 引言
自生命诞生以来,追逃博弈问题就广泛存在于自然界,是捕食者与被捕食者之间的生死游戏。而随着人类科技的飞速发展,追逃博弈问题的研究也从生物之间的博弈转变为人类造物之间的博弈,追踪者想方设法地追上逃逸者,而逃逸者则尽可能远离追踪者,根据各自的策略完成博弈。
追逃博弈问题最早于1965年被提出。2014年,J.Y.Kuo等为解决动态环境下的追逃博弈问题,运用概率论与图式理论为追踪者设计了一种认知行为学习机制,首先通过意向图式预测逃逸者的位置,之后通过感知图式为追踪者选择动作,为追踪者处于未知环境下的追踪问题提出了一种解决方法[1]。2019年,在主动防御的三者博弈场景中,Sun Q.等基于微分对策设计了一种制导律,使得追踪者在无法获知目标与防御者加速度的情况下完成对目标的追踪,并完成对防御者的躲避[2]。
随着人工智能技术的飞速发展,许多应用领域均产生了智能化的趋势。由于环境与任务目标的复杂性,在实际应用中单个智能体往往无法顺利完成目标,需要多个智能体进行协同合作[3],甚至可能面临多个智能体之间的竞争博弈[4]。多智能体追逃问题同时存在竞争博弈与协同合作,是研究多智能体的一种良好平台。
近年来,国内外学者尝试将强化学习方法引入追逃博弈问题研究之中。2011年,J.Y.Kuo等就通过Q学习(Q-Learning)[5]实现了单个追踪者的追踪策略学习,并基于案例推理实现了多智能体之间的协同学习[6]。2017年,针对超级逃逸者,即逃逸者的最大速度超过所有追踪者的最大速度的围捕问题,A.A.Al-Talabi提出了一种模糊强化学习方法,使得追踪者通过分散的方式捕获单个超级逃逸者,并通过编队控制策略避免碰撞,而逃逸者使用阿氏圆寻找追踪者之间的空隙[7]。在追逃博弈中,追踪者往往在与训练环境类似的场景中进行决策,若环境改变则追踪策略可能失效。为解决此问题,M.D.Awheda等提出了一种模糊强化学习算法,增强了追踪者在与训练环境不同的场景中捕获逃逸者的能力[8]。2018年,针对二维平面中智能小车的追逃问题,谭浪等设计了一种基于深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)算法[9]的追逃博弈算法[10]。2019年,Wang L.等将DDPG与模糊理论相结合,克服了原算法依赖概率分布的缺点[11]。通常在追逃游戏中,对运动学约束进行简化,并假设空间中没有障碍物。2020年,Qi Q.等在考虑智能体运动学与环境静态障碍物的情况下,提出了一种课程深度强化学习方法,追踪者与逃逸者通过自我博弈的机制同时进行训练,并通过课程学习的方法逐步增加学习任务难度[12]。针对智能体数量增多时群体强化学习算法状态空间过大难以收敛的问题,刘强等提出了一种带注意力机制的群体对抗策略,智能体只关注自身周围的智能体,有效减少了Critic网络的计算复杂度[13]。
上述方法中,多智能体追逃博弈通常在二维平面场景下进行,且逃逸方智能体运动不受约束。考虑到任务状况的复杂性,智能体往往不会局限于二维空间,且可能受到运动能力约束。因此,本文针对逃逸方智能体运动受约束的三维空间追逃问题,设计了一种基于深度Q网络(Deep Q-Network,DQN)[14-15]的多智能体逃逸算法,并通过引入强化学习方法,解决了无法对智能体准确建模时难以设计控制策略的问题,同时根据任务难易程度将智能体逃逸策略学习分为两个阶段,有效提高了学习效果。
1 多智能体逃逸问题描述
本文中研究的多智能体问题为三维空间环境下的逃逸问题。为便于逃逸算法问题本身的研究,将该问题简化为质点的运动学问题,忽略智能体的外形与姿态变化。
双方智能体在三维空间中初始距离为2km,且相向运动,图1所示为该场景示意图。逃逸方与追踪方均有3个智能体,逃逸方智能体速度较快,但受到运动约束,只可在法向进行固定方向的离散机动,即y与z方向,如图1右上角所示,且逃逸方智能体机动次数受到约束,只能进行有限次的法向机动;追踪方智能体则可在法向进行无限制持续机动,对逃逸方智能体进行追踪。双方智能体各项运动学参数如表1所示。

图1 多智能体追逃环境示意图Fig.1 Schematic diagram of multi-agent pursuit-evasion environment

表1 智能体运动学参数
追踪任务开始时,追踪方智能体依次锁定距离其最近的一个尚未被追踪的逃逸方智能体,逃逸方智能体通过在环境中不断地探索学习得到一种合适的逃逸策略,该逃逸策略可使逃逸方智能体成功完成逃逸。
2 多智能体逃逸算法设计
2.1 多智能体逃逸算法框架
多智能体逃逸算法以DQN算法为核心,并可基于已有训练结果进行再训练,算法总体框架如图2所示。

图2 多智能体逃逸算法框架Fig.2 Multi-agent evasion algorithm framework
若已有训练结果与当前训练时的奖励函数不同,则在训练前需对网络进行初始化,即此时已有训练结果用于帮助智能体在训练前获得高质量的训练经验。图2中红色虚线框中的部分为运用DQN算法学习多智能体逃逸策略的主要部分,即DQN网络更新在此部分完成。在多智能体逃逸算法中,智能体通过训练不断改进自身逃逸策略,并将已有训练结果当作先验知识,有效降低了训练难度,提高了训练效率。
2.2 DQN算法
DQN算法由Deep Mind公司提出,首次将深度神经网络与强化学习相结合,利用神经网络感知环境并进行决策,解决了Q-learning只能应用于离散状态空间的情况。同时,为解决神经网络训练在时序样本数据下的收敛问题,引入了经验回放单元与估计值-目标值网络两种机制。式(1)与式(2)分别给出了DQN算法中值函数的迭代公式与Q网络的损失函数。

(1)
(2)

2.3 多智能体逃逸算法网络设计
逃逸方智能体采用分布式学习的方法,即每个智能体独立使用一个Q网络,系统输入的状态为逃逸方和追踪方之间的相对距离和视线角与视线角速率信息,输出为智能体的机动动作,其中包括智能体法向上的不机动、单个方向机动与两个方向同时机动的九种机动动作,逃逸者机动方式如图3所示,算法整体框架如图4所示。
在该算法中,神经网络的输入为上述5个系统状态,输出为智能体的九种动作,由于输入状态与输出动作数量较少,因此采用三层全连接神经网络,神经网络结构参数如表2所示。

图3 逃逸者机动方式Fig.3 Maneuvers of the evader
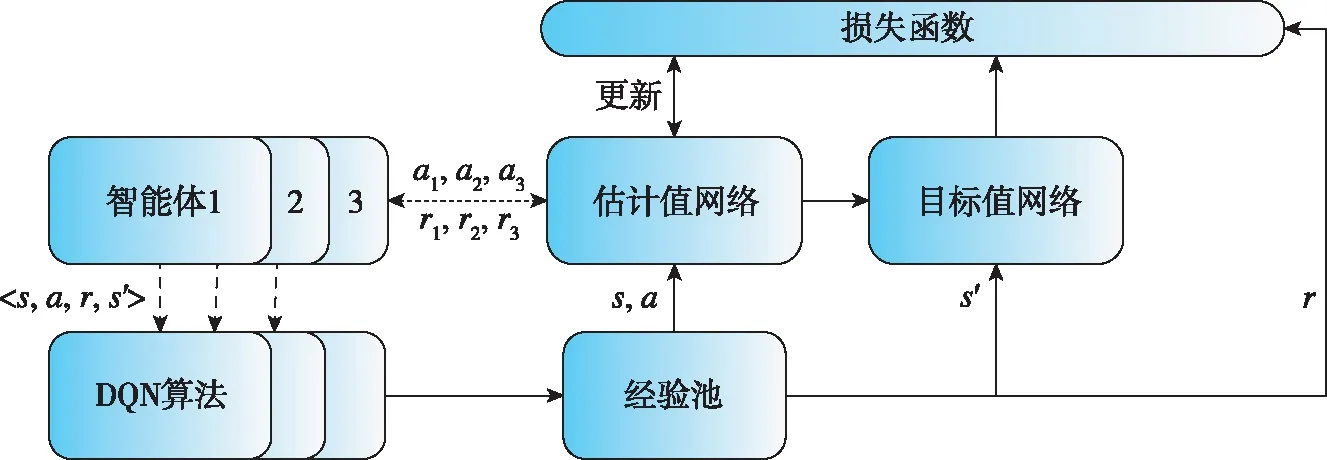
图4 分布式多智能体DQN算法框架Fig.4 Distributed multi-agent DQN algorithm framework

表2 神经网络结构参数
2.4 多智能体逃逸算法奖励函数设计
为加快智能体学习效率,利用课程学习的思想,对任务目标进行分解,使智能体根据任务难度由易到难分阶段进行学习。在第一阶段中,智能体通过学习寻找可以成功逃逸的机动策略,而对逃逸能力的强弱不作要求。因此,当逃逸方智能体成功逃逸时,获得一个大的终端奖励,终端奖励函数为
(3)
由于逃逸方智能体存在机动时间限制,为更好利用有限的机动能力进行逃逸,鼓励智能体探索更优的逃逸策略,设计了智能体逃逸时的过程奖励r2
(4)
其中,qe为视线倾角;qb为视线偏角;t为仿真时间;智能体机动动作编号0为不机动,1~4为单方向机动,5~8为双方向同时机动。智能体的过程奖励主要取决于视线角的大小,由于初始视线角趋近于0,因此当视线角变大时,视为智能体更有可能完成逃逸。而过程奖励的系数取决于智能体机动与机动时机。由于逃逸方智能体机动次数受限,因此设置单方向机动或不机动时,即动作编号0~4的奖励系数为200,较两个方向机动时的系数50更大,以鼓励智能体进行更长时间的机动,增强机动能力的利用效率。同时,过程奖励系数与仿真时间相关,逃逸方越晚机动,留给追踪方的机动时间越少,更易完成逃逸,但是机动时间过晚逃逸方机动空间则会变小。因此,随着时间t的增加,奖励系数变大,鼓励逃逸方智能体尽可能晚的机动。
由于第一阶段训练没有针对逃逸能力进行针对性的强化,因此智能体无法充分运用自身机动能力。当面临新的初始环境条件时,原来在训练中恰好可以完成逃逸的策略可能就会失效。因此,智能体将在第一阶段任务学习的基础上进行训练,第二阶段的训练任务是尽可能地增强逃逸方智能体的逃逸能力,即尽可能地远离追踪者。
智能体在进行第二阶段任务学习之前,依靠第一阶段学习所得逃逸策略产生更有价值的数据,并将其填入经验池中供智能体学习。由于此阶段中逃逸方智能体的目标是最大化逃逸能力,因此在训练时有针对性地选用成功逃逸的经验数据进行学习。基于第二阶段任务的目标,即逃逸方智能体尽可能地远离追踪者,对智能体的终端奖励进行了改进,如式(5)所示
(5)
其中,dmin为逃逸过程中双方智能体之间的最小距离,这项指标体现了智能体的逃逸能力。当此距离越大时,逃逸方智能体获得的奖励越大,从而鼓励智能体优化其策略,使得智能体可以充分利用其机动能力完成更有效的逃逸。
智能体获取的奖励为其过程奖励与终端奖励之和
r=r1+r2
(6)
综上所述,基于DQN的多智能体逃逸算法流程如表3所示。

表3 基于DQN的多智能体逃逸算法
3 仿真实验与分析
对智能体进行了两个阶段四次(共3600回合)的训练。由于在逃逸方智能体不机动或随机机动时,追踪方智能体在当前双方机动能力下总能接近至0.5cm,因此设置当双方智能体最小相对距离大于0.5cm时视为逃逸成功,并在第二阶段中对该指标进行优化,其中第一次到第三次训练为第一阶段,第四次训练为第二阶段。设置探索概率随着回合数的增加,从初始探索概率0.9逐渐下降至0.1,奖励折扣系数γ为0.9,学习率α为0.01,第一阶段与第二阶段经验池大小分别为5000与2000。训练结果如表4所示。

表4 多智能体逃逸算法训练结果
对训练所得逃逸策略进行测试,最终3个逃逸方智能体的逃逸最小距离分别为44.53cm、47.32cm及44.53cm。智能体运动轨迹仿真结果如图5所示,图6所示为其局部放大图,其中每行代表不同的追逃双方智能体,第一列至第三列分别表示追逃双方智能体间的距离与双方智能体在OXY与OXZ平面内的位置。
根据图5与图6可以看出,逃逸方智能体在经过学习后,可以通过学习所得的逃逸策略完成逃逸。根据图6中第一列的局部放大图可以看出,在该训练环境下追逃双方智能体在运动过程中的最小距离为0.5m左右。

图5 多智能体逃逸算法仿真结果Fig.5 Simulation results of multi-agent evasion algorithm

图6 仿真结果局部放大图Fig.6 Partial enlargement of simulation results
图7给出了两个阶段的学习曲线,其中第一阶段取每150回合的平均累计奖励值,第二阶段取每50回合的平均累计奖励值,可以观察得出累计奖励在一定回合后收敛于某一区间内。
若不将智能体的策略学习分为由易到难的两个阶段,智能体会直接采用第二阶段的奖励函数学习逃逸策略,其余训练参数相同。在经过相同回合的学习后,智能体的训练结果如表5所示。图8则给出了不分阶段的智能体逃逸策略学习曲线,并取每150回合的平均累计奖励值。将表5与图8分别与表4与图7对比可以看出,若不分阶段,智能体的策略学习难度较大,最终智能体难以习得可用的逃逸策略。由此可得,根据任务难度将智能体逃逸策略学习分为两个阶段,可有效提升智能体的策略学习效果。

图7 多智能体逃逸算法学习曲线Fig.7 Learning curve of multi-agent evasion algorithm

表5 不分阶段的训练结果

图8 不分阶段的学习曲线Fig.8 Learning curve without stages
由于逃逸方智能体只可进行总长为1s的机动,根据经验可知,逃逸方智能体在距离较近时机动逃逸能力较强,而距离过近时则由于时间不足无法完成逃逸。对强化学习机动启动时刻进行对比,结果如表6所示,可以看出,当逃逸方智能体在双方相距200m时,智能体可以在探索概率较大时,即较早的回合得到逃逸成功的样本数据,并且同样经过1500回合的学习后,启动距离为200m比300m获得的成功样本数据更多,由此可以证明当启动距离选择为200m时开始强化学习机动效果较好。

表6 强化学习机动启动时刻效果对比
为了测试算法效果,采用与训练不同的初始条件对学习所得逃逸策略进行泛化测试,逃逸方智能体初始位置在YOZ平面中200m×200m的范围内进行均匀随机取样,测试结果如图9所示。
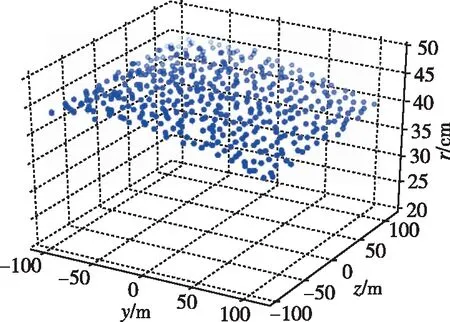
(a)智能体1
为检测逃逸策略的稳定性,对测试结果求均值与标准差,结果如表7所示。

表7 算法泛化测试结果
仿真结果表明,逃逸方智能体采用所学逃逸策略在初始位置200m×200m范围内均可成功完成逃逸,具有较好的泛化能力,逃逸能力稳定,逃逸最小距离平均在40cm以上,且波动较小,表明逃逸方智能体可以通过该算法学习得到合适的逃逸策略。
4 结论
1)本文针对三维空间下的多智能体逃逸问题,设计了一种基于DQN的多智能体逃逸算法。该算法采用分布式学习的方法,多个智能体分别使用一个DQN进行决策。通过引入DQN算法,使得智能体可以在不需要系统模型的情况下,通过对环境不断地探索与学习,仅需要双方智能体相对距离与视线角等少量的环境状态,即可得到符合期望的多智能体逃逸策略,并对学习任务进行分解,将其分为基础任务与进阶任务,降低了智能体逃逸策略的学习难度。
2)仿真结果表明,逃逸方智能体在不同的初始位置条件下均可以使用学习所得的逃逸策略完成逃逸,逃逸能力稳定,并且根据其初始位置的不同呈一定的趋势,表明该算法在训练中得到有效收敛。
3)本文算法为针对三对三的追逃问题所设计,若拓展到不同场景不同智能体数量的情况下,需对算法的结构与奖励函数进一步设计,拟在后续研究中增强算法的泛化能力,使其在不同场景下均可完成决策。
4)在仿真实验中发现,算法在第二阶段任务中不能保证收敛,同时同方智能体间缺乏协同合作,拟在后续研究中尝试集中式学习算法,以增强同方智能体之间的交互合作,并增加双方智能体博弈竞争的复杂度,将尝试改进算法的神经网络结构与借鉴课程学习的思想,以克服策略收敛问题。
