低信噪比下多目标调制谱轴频自动检测算法

2023-01-03王易川程玉胜

振动与冲击 2022年24期

马凯，陈喆，王易川，程玉胜

(海军潜艇学院，山东青岛 266000)

舰船辐射噪声[1]调制谱特征是水声目标识别的重要特征，具有很好的稳健性。对调制谱进行谐波分析可以获得螺旋桨的轴频、叶频和桨叶数等特征[2-4]，其中，轴频提取对目标识别具有重要意义。

许多学者对轴频地提取进行了深入研究[5-6]。文献[7]模拟声纳兵处理DEMON(detection of modulation spectrum on noise)谱的方法，利用双门限提高了水声目标辐射噪声调制谱检测能力，并通过提取到的线谱间隔估计轴频，算法在单目标情况下效果较好。文献[8]通过最大公约数法提取目标轴频，但最大公约数法在某些多目标情况下不适用。Di Martino等[9]提出一种基于代价函数的线谱提取算法，用于低频线谱地提取。该算法通过设定一代价函数，使符合线谱特征的点可以提取出来，对于弱线谱地提取效果较好，但该算法只能提取单根线谱。李山等[10]通过设定频率滑动窗实现了多根线谱地提取，但算法并不是全局最优的，当信噪比较低时，算法效果并不理想。针对上述情况，本文提出一种基于蚁群算法的调制谱线谱提取算法。蚁群算法是由Dorigo等[11]提出的一种比较成熟的全局优化算法，被广泛应用于机器人路径规划、任务规划问题等[12-15]。该算法是一种模拟蚂蚁觅食行为的智能群算法，具有正反馈、强鲁棒性、并行性、较好的适应性等优点[16]。

1 基于蚁群算法的线谱提取算法

蚁群算法的原理源于模拟蚂蚁种群的觅食行为，蚂蚁在觅食时会在搜寻路径上留下一种名为信息素的分泌物，经过此路径的蚂蚁越多，信息素浓度就越高。而信息素会对后面的蚂蚁产生一种正向的吸引作用，即信息素浓度越大，则后面的蚂蚁选择此条路线的概率越大。同时，部分信息素会挥发，有利于蚁群进行其他路线的搜索，提高全局搜索能力，避免陷入局部最优。

本文将调制谱中的轴频及其倍频线谱视为蚂蚁寻优的“路径”，通过改进寻优策略，使其适用于调制谱中线谱地提取。

1.1 蚁群算法描述

蚁群算法的状态转移概率公式为

(1)

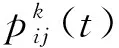
(2)

式中，dij为节点i到节点j的距离。

蚂蚁每完成一次循环后路径信息素更新为

τij(t+1)=(1-ρ)τij(t)+Δτij(t)

(3)

(4)

式中：τij(t+1)为更新后节点i到节点j的信息素强度；ρ为信息素挥发系数；m为蚁群数量；k为第k只蚂蚁；Δτij(t)为节点i到节点j的信息素增加量，其中Δτij(t)的计算方式采用蚁周型，如式(5)所示。

(5)

式中：Q为信息素增加的强度系数；Lk为循环结束后蚂蚁经过的路径长度。

1.2 基于蚁群算法的线谱提取算法

采用栅格法[17]将DEMON谱图划分成一个个小方格，将蚂蚁随机布放于小方格之中，令其对整个DEMON谱图进行搜索。其中，在应用算法时存在以下几个问题。

(1) 在经典的蚁群算法中，蚂蚁可以随机选择周围8个方向进行搜寻，如图1所示。但在DEMON谱图中，每条线谱在每一时刻的频率是单一的，即蚂蚁只能随着时间增加或减少的方向进行搜索，而不能横向搜索。

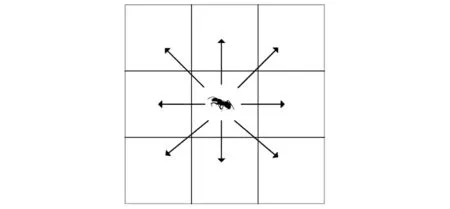
图1 蚂蚁可选搜寻方向图Fig.1 Available search directions for ants

(2) 在经典蚁群算法中，蚂蚁的出发点和目的地一般是固定的，而在DEMON谱图中，蚂蚁的出发点则位于起始时刻任意频率点处，目的地位于终止时刻任意频率点处，位置不固定。

(3) 在经典蚁群算法中，启发函数以及信息素的更新是根据蚂蚁距目的地的距离来确定的，而在DEMON 谱图中，由于“目的地”未知，所以无法依据“距离”这一标准来确定。

基于以上几点问题，提出一种基于蚁群算法的线谱提取算法，并作以下改进。

(1) 对蚂蚁的搜寻范围进行限定，即每只蚂蚁只能在时间轴方向进行搜索，而不能横向搜索，如图2所示。纵坐标为时间，横坐标为频率。

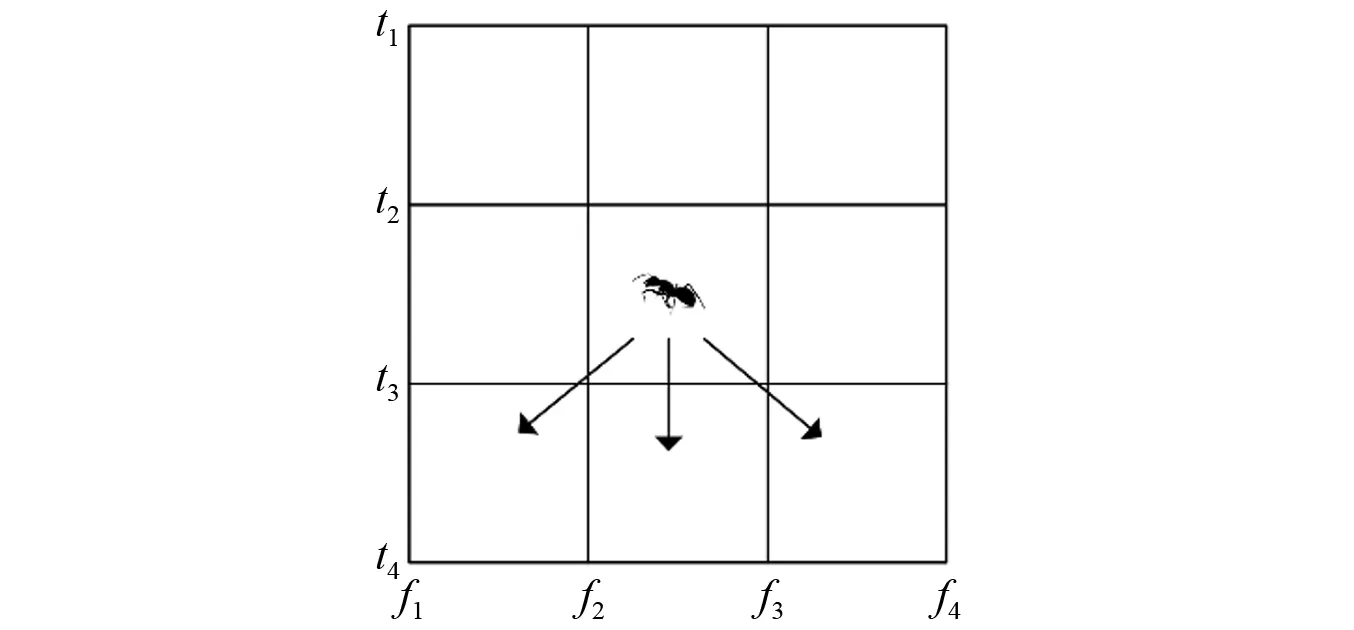
图2 蚂蚁在DEMON谱图中的可选搜寻方向图Fig.2 Available search directions for ants in lofargram

(2) 提出一种新的代价函数作为决定启发函数和信息素更新的标准，如式(6)所示。

(6)

式中：ξ为线谱路径；d(i)为线谱的频率连续性特征；G(i)为线谱的轨迹连续性特征；A(i)为线谱的强度特征，即线谱路径上的各个频率点上的幅值；eps为算法精度，用以防止出现分母为0的情况。则由式(5)可知，当线谱的能量越强，即A(i)越大，频率连续性越好，即d(i)越小，轨迹连续性越好，即G(i)越大，则线谱代价函数越小，即P_cos(ξ)越小。

d(i)，G(i)，A(i)的定义式分别为

d(i)=|f(Pi)-f(Pi+1)|+eps

(7)

(8)

(9)

式中：f(Pi)为线谱Pi在i点处的频率值；g(Pi)为一个标记变量，其定义如式(9)所示，即当g(Pi)小于设定的线谱幅值门限count时，则认为此处出现断点，否则设为1。

则新的启发函数为

(10)

由式(10)可知，P_cos(ξ)越小，即搜寻路径越接近线谱时，启发函数值越大，符合启发函数的设计原则。

(3) 随着迭代次数的增加，路径上的信息素浓度易积累过高，导致蚂蚁的路径选择能力在一定程度上降低，极可能增加陷入局部最优解的概率。因此，对信息素增加的强度系数Q进行改进，使其随迭代次数的增加自适应的调整，如式(11)所示，当迭代次数大于设定的阈值时，Q值随迭代次数的增加逐渐减小，从而降低算法陷入局部最优的概率。

(11)

式中，Ne为当前迭代次数。

算法处理流程，如图3所示。其中C为设定的迭代次数。

算法处理步骤如下：

步骤1对获取的信号进行解调处理，得到DEMON谱图，并将其栅格化处理。

步骤2初始化禁忌表，禁忌表用以记录蚂蚁访问过的节点。

步骤3将M只蚂蚁随机放置于DEMON谱图起始时刻的各频率点处，并计算每只蚂蚁到下个节点的代价函数P_cos(ξ)。

步骤4由代价函数P_cos(ξ)计算得到启发因子ηij(t)。

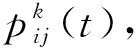
步骤6更新禁忌表，并记录每只蚂蚁走过的路径。

步骤7当蚂蚁遍历整个DEMON谱图的时间轴时，一次迭代结束，并重复上述过程。

步骤8记录代价函数最小的n条路径，并进行二次阈值判断，最终得到所需要的线谱。

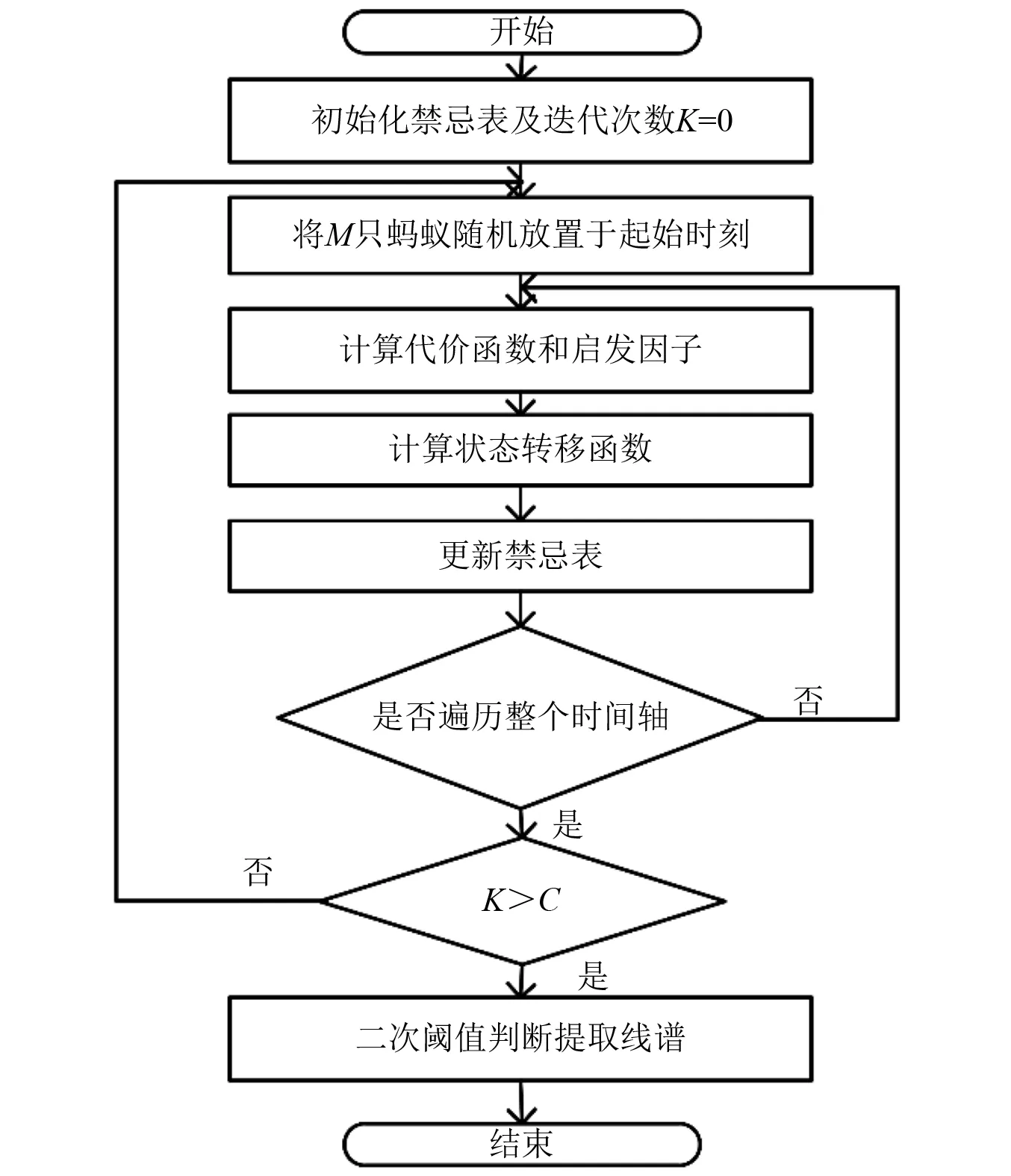
图3 算法处理流程图Fig.3 Flowchart of algorithm processing

2 谐波库匹配算法

由于螺旋桨结构设计以及环境等因素，所提取的线谱中可能会包含虚假线谱，也可能缺失轴频及其谐波线谱。并且，在多目标情况下，线谱结构更复杂，轴频地自动提取也更困难。常用的轴频提取算法包括最大公约数法、余数门限法[19]、倍频法等，此类算法在某些多目标情况下效果较差。针对这种情况，提出一种谐波库匹配算法，自动提取多目标轴频。

算法处理流程如下：

步骤1将提取到的n条线谱从小到大排列，得到线谱序列{fm}，m=1,2,…,M。

步骤2根据现有船舶螺旋桨结构可知，螺旋桨桨叶数通常最多为7叶。因此，根据已经提取的n条线谱建立一个大小为n×7的谐波库矩阵H。

步骤3将每根线谱fm分别假设为轴频的1～7次谐波，其中1次谐波为轴频。定义一品质因数Sk，用以记录fm为k次谐波时，序列{fm}中符合式(12)条件的线谱个数。

(12)

式中，Δ为误差控制量，依据实际情况确定，用以表示由非严格谐波情况造成的误差。

步骤4将线谱fm的品质因数Sk存入谐波库H(m,k)中，统计每条线谱fm中品质因数最大时的谐波次数kmax，并按照式(13)计算出线谱fm的基频Bm。

(13)

步骤5此时，基频序列{Bm}中可能由于非严格谐波关系存在弱小的误差，将{Bm}中的每个基频返回到DEMON谱图中，分别计算基频为Bm时的各线谱的能量Pm。

步骤6将频率之差小于δHz的基频归为一类，分别计算每一类中Pm最大时的基频Bm，并比较这几类中Pm值的大小，取最大的两个P1和P2,其中P1≥P2，若P2大于噪声背景均值，则基频为B1和B2，否则，认为目标为单目标，基频为B1。

3 仿真及试验验证

3.1 算法处理流程

本文算法处理流程，如图4所示。

步骤1对输入信号S进行绝对值解调，获得DEMON谱。

步骤2利用文献[20]中的排序截短算法对DEMON谱进行背景均衡，剔除趋势项。

步骤3通过提出的蚁群算法提取DEMON谱中的线谱。

步骤4利用谐波库匹配算法实现多目标信号轴频地自动提取。

图4 本文算法处理流程图Fig.4 Algorithm processing flow chart of this paper

3.2 仿真验证

仿真中假设有两个目标，轴频分别为6 Hz，9 Hz，5叶桨，信噪比设为-17 dB，采样频率为5 000 Hz，其中在15 Hz处添加了一条干扰线谱，并且为了模拟实际信号中的非严格周期现象，分别在轴频倍频处加入一弱小的扰动。仿真参数设置：α=7，β=7，Rho=0.1，Q=100，m=400，L=100，所有参数均经过蒙特卡洛仿真试验确定，综合性能最优。

3.2.1 背景均衡

解调后的原始的DEMON谱图，如图5所示。背景均衡后的DEMON谱图，如图6所示。由图5、图6可知，此时信噪比较低，线谱能量较弱，部分线谱几乎不可见，经过背景均衡，剔除趋势项后，算法的背景噪声有所降低。

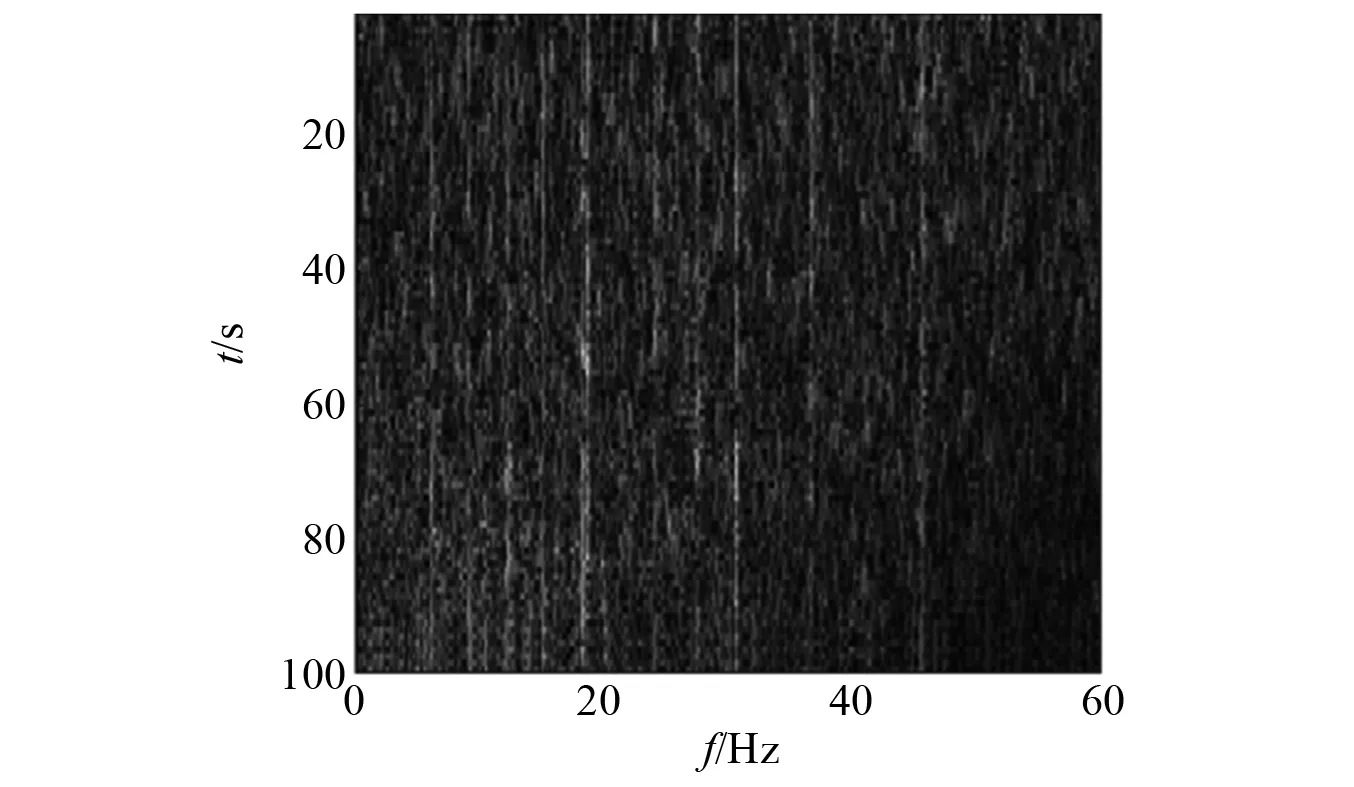
图5 原始DEMON谱图Fig.5 Original DEMON

图6 背景均衡后的DEMON谱图Fig.6 DEMON after background equalization

3.2.2 线谱提取

经过最优路径算法和本文提出的蚁群算法所提出的线谱，如图7和图8所示。由图7、图8可知，最优路径算法可以提取部分较弱的线谱，但同时会遗漏部分线谱，如18 Hz附近的两条线谱会漏掉一根。本文所提算法效果较好，即使部分肉眼几乎不可见的线谱也能较好地提取出来。

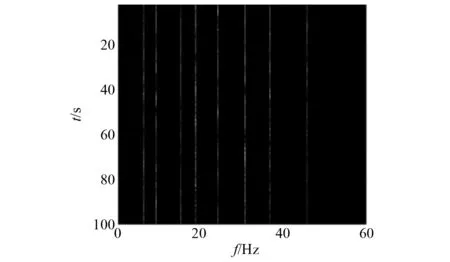
图7 最优路径算法所提线谱Fig.7 Line spectra proposed by optimal path algorithm

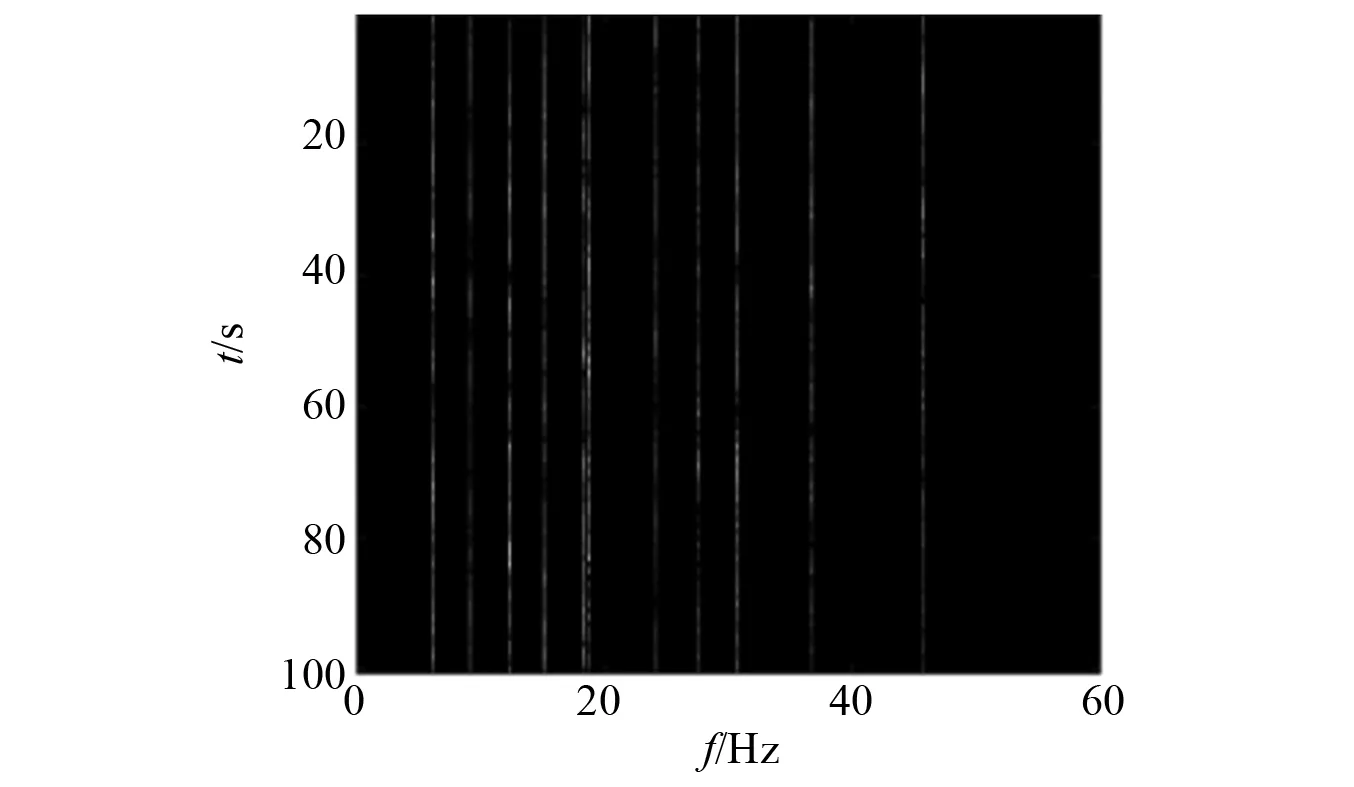
图8 本文算法所提线谱Fig.8 Line spectra proposed by the algorithm in this paper

不同信噪比下，两种算法线谱提取性能的比较，如图9所示。为了比较两种算法的线谱提取能力，现定义线谱提取率P，如式(14)所示。由图9可知，最优路径算法无法提取相邻较近的两根线谱，其线谱提取的准确率始终低于本文算法。这是因为本文所提算法是一种全局寻优的算法，当信噪比较低时，算法受离散能量较高的噪点的影响较小，而最优路径算法受能量较高的噪点的影响较大，从而提取能力随信噪比的降低下降较为严重。但本文算法花费时间较最优路径算法长，用时15 s，最优路径算法用时5 s，下一步将通过并行处理等手段提高算法的运算速度。

(14)

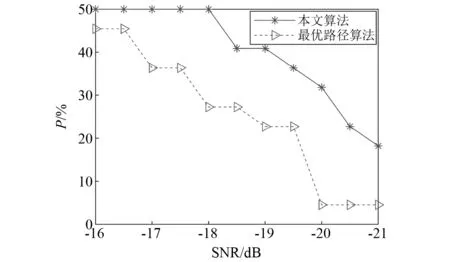
图9 两种算法的线谱提取性能对比图Fig.9 Comparison of the extraction performance of the two algorithms

3.2.3 轴频自动提取

(1) 最大公约数法

该算法首先计算了所提线谱中任意两条线谱之差，并定义了3种品质因数：Sq1，Sq2和Sq3。其中：Sq1为上述差值中相同数的个数；Sq2为上述差值中能被所提线谱频率除尽的数的个数；Sq3为Sq1和Sq2的乘积，Sq3最大时所对应的频率即为轴频。Sq3最大值为77，所对应的频率为3 Hz，很明显不是所求轴频，所以该算法在某些多目标情况下不适用，如表1所示。

表1 最大公约数法所得结果Tab.1 Results obtained by the maximum common divisor method

(2) 余数门限法

该算法首先定义了一个3×n的矩阵，n为设定的线谱的个数，矩阵的第一列用于存放线谱，第二列存放线谱的初始权值ω，第三列存放判决依据F，F最大时所对应的频率即为所求轴频，如表2所示。由表2可知，当F最大时，频率为9 Hz，即所求轴频为9 Hz，只能求得其中的某一个目标的轴频，因此该算法在某些多目标情况下是不适用的。

表2 余数门限法所得结果Tab.2 Results obtained by the remainder threshold algorithm

(3) 谐波库匹配算法

本文所提算法经式(12)处理后的基频，如表3所示。由表3可知，算法得到的基频分为两类，每一类中的Pm的最大值所对应的基频分别为6 Hz和9 Hz，与噪声背景均值比较最终可得目标的轴频分别为6 Hz和9 Hz，与仿真设定的轴频一致，效果较好。

表3 本文算法所得结果Tab.3 The results obtained by the algorithm in this paper

3.3 海试数据验证

该信号为多目标信号，经过先验信息以及人工综合判定，确定两目标轴频分别为1.52 Hz和1.88 Hz，信号采样频率为44 100 Hz，频率分辨率为0.01 Hz，线谱提取参数设置同仿真。

3.3.1 背景均衡

解调后的原始DEMON谱图，如图10所示。其中部分线谱能量较弱，几乎淹没于背景噪声中。背景均衡后的DEMON谱图，如图11所示。经过背景均衡，算法的背景噪声有所降低。

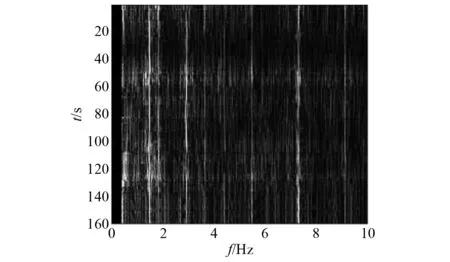
图10 原始DEMON谱图(海试数据)Fig.10 Original DEMON(sea trial data)

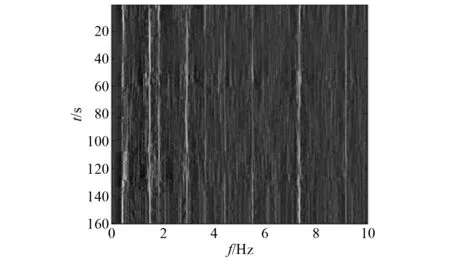
图11 背景均衡后的DEMON谱图(海试数据)Fig.11 DEMON after background equalization(sea trial data)

3.3.2 线谱提取

经过最优路径算法和本文提出的蚁群算法所提出的线谱，如图12和图13所示。由图12、图13可知，最优路径算法可以提取部分较弱的线谱，但同时会遗漏部分线谱，例如2.96 Hz，4.44 Hz处的线谱。本文所提算法可以将能量非常低的线谱提取出来，效果较好。

图12 最优路径算法所提线谱(海试数据)Fig.12 Line spectra proposed by optimal path algorithm(sea trial data)

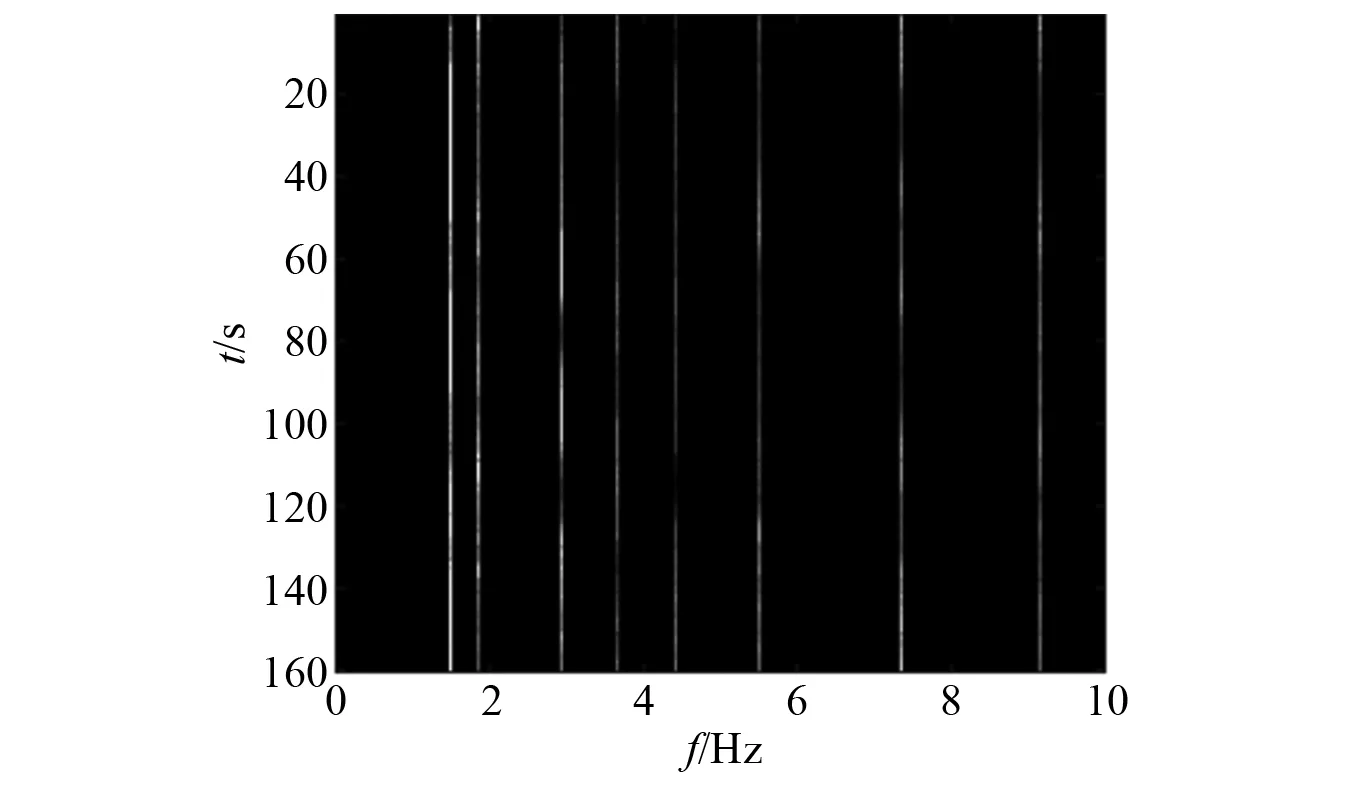
图13 本文算法所提线谱(海试数据)Fig.13 Line spectra proposed by the algorithm in this paper(sea trial data)

3.3.3 轴频自动提取

最大公约数法得到的结果，如表4所示。Sq3最大值为20，所对应的频率为1.82 Hz，与实际轴频有所差距，并且只能提取单个轴频，效果欠佳。

余数门限法所求结果，如表5所示。当F最大时对应的频率为1.52 Hz，即所求轴频为1.52 Hz，只能求得单个目标的轴频，因此在某些多目标情况下是不适用的。

表4 最大公约数法所得结果(海试数据)Tab.4 Results obtained by the maximum common divisor method(sea trial data)

表5 余数门限法所得结果(海试数据)Tab.5 Results obtained by the remainder threshold algorithm(sea trial data)

本文所提算法的结果，如表6所示。由表6可知，算法得到的基频分为两类，每一类中的Pm的最大值所对应的基频分别为1.52 Hz和1.88 Hz，取其中最大的两个值并与噪声背景均值比较，最终可得，目标的轴频分别为1.52 Hz和1.88 Hz，与实际轴频一致，效果较好。

表6 本文算法所得结果(海试数据)Tab.6 The results obtained by the algorithm in this paper (sea trial data)

综上分析可知，本文所提出的基于蚁群算法的线谱提取算法相较于最优路径算法效果更好，可以提出能量很弱的线谱；在多目标条件下，提出的基于谐波库匹配算法相比于过去的最大公约数法以及余数门限法效果更好。最大公约数法及余数门限法在某些多目标情况下所提出的轴频可能不是真实轴频，且只能提取单个轴频，本文算法则能够解决此问题。