基于标准磁块模型的赤道作图法误差分析
2023-01-03徐超群周腊琴张绍华刘超波张艳景耿晓磊
徐超群,肖 琦,周腊琴,张绍华,刘超波,张艳景,李 娜,耿晓磊,王 琪
(北京卫星环境工程研究所,北京 100094)
0 引言
空间磁场[1]是中低轨道卫星在轨运行环境的要素之一,可对卫星产生潜在、长期累积的磁效应,影响卫星飞行姿态及星上磁敏感仪器的正常工作。因此对于中低轨道、磁场科考类磁控制要求高的卫星[2],必须准确测量和控制其磁特性,确保卫星在轨的磁姿态及磁探测仪技术指标满足控制要求,以提高卫星在轨寿命和可靠性。
卫星地面磁测试采用的主要方法有力矩法和作图法等。力矩法需要使用力矩计及其他复杂的地面测试配套设备。作图法中的磁偶极子法[3]多用于试件磁矩的预测和量级评估;球面作图法需测量获取卫星包络球面上大量磁场数据,试验精度相对高,但该方法的磁测试工艺流程要求对卫星执行翻转操作,存在安全风险;相较而言,赤道作图法[4]是卫星磁试验中最经典且安全的测试方法。需要指出的是,作图法测试布局对卫星尺寸和传感器测试距离的比例有特殊要求。其他方法,如动态环路法[5]、欧拉方法[6]等,多用于小型试件的磁矩测量和磁矩分析,且:动态环路法易受卫星外形影响,对环路线圈尺寸变化有一定的要求;欧拉方法仅对卫星内部的多磁偶极子进行分辨,实用性和准确率均不高。
赤道作图法在卫星磁矩测量的操作性、安全性和准确性方面较其他方法都有一定的优势,是目前主要的卫星磁测试方法。随着空间技术的发展,一些科学卫星的磁矩测量精度要求越来越高。本文从基本理论出发,基于标准磁块模型对赤道作图法在卫星磁试验中的部分误差因素进行分析,针对背景磁场干扰误差提出近远场梯度差分的方法以提高近场算法的准确度,并通过地面试验对误差控制措施实施效果进行验证。
1 卫星磁偶极子模型
卫星构型复杂、磁化不均匀,为了计算和描述其磁特性(磁矩和磁场分布),把卫星简化成一个长方体,其内每个磁源等效为一个磁偶极子[7-8],将磁源按原空间位置分布在长方体的内部,建立卫星磁偶极子模型(见图1)进行磁场数据测量与计算。图中,红点代表磁源,红线代表磁矩。
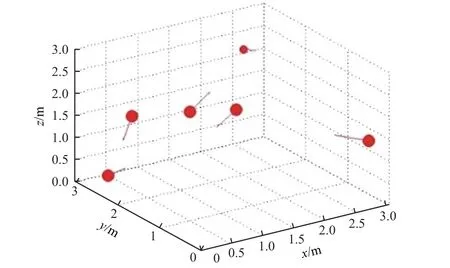
图1 卫星磁偶极子模型Fig. 1 Magnetic dipole model of a satellite
2 赤道作图法测量和计算原理
2.1 磁强计布局及测量方式
目前,地面实验室[7]利用赤道作图法测量卫星及其部件磁矩的传感器布局方式如图2 所示,将试件放置于转台上,在与试件几何中心不同距离处布置3 个三分量磁通门磁强计(r1、r2、r3分别为1~3 号磁强计探头中心到试件几何中心的距离),每旋转转台10°(或20°)采集1 组磁场数据,直到旋转360°获取试件赤道面1 周的全部磁场数据,以供后续进行磁矩计算。
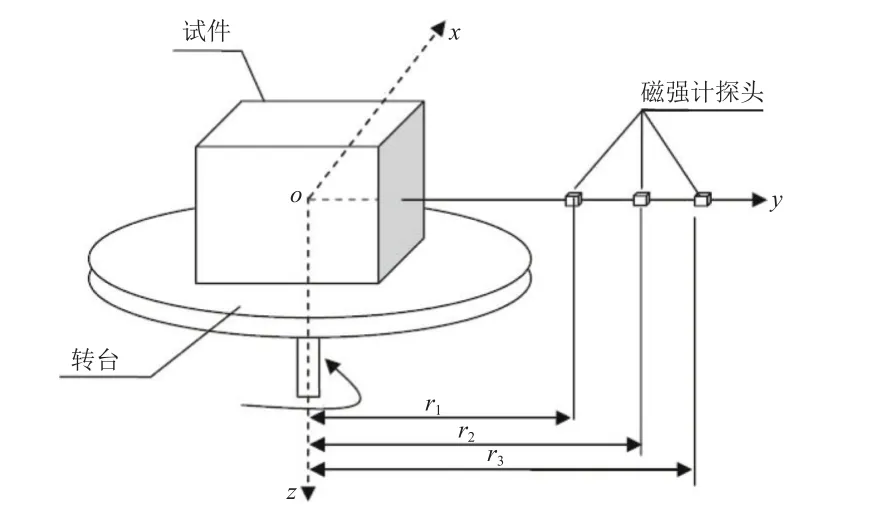
图2 磁测试布局示意Fig. 2 Schematic of the magnetic test layout
2.2 磁矩计算方法
赤道作图法以卫星磁偶极子模型为基础,利用磁强计收集试件赤道面1 周的磁场数据,对数据进行偶极化处理得到磁矩[9]。具体计算方法如下:
首先,进行第1 次磁感应强度偶极化处理,令
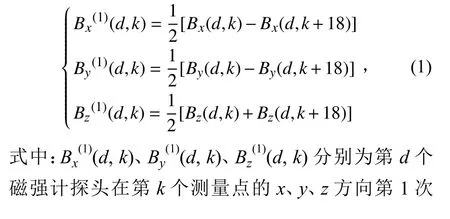

磁矩M的计算式为

3 误差来源及控制措施
磁矩测量(计算)相对误差的定义为
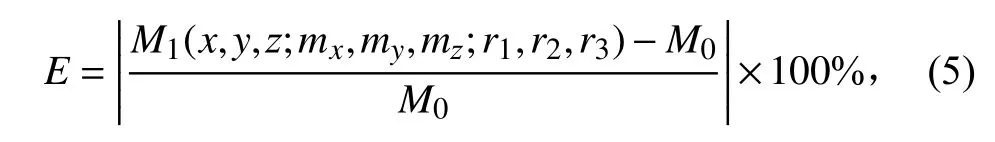
式中:M1为试件磁矩测量(计算)值,包含试件位置、试件磁矩三分量以及试件与磁强计距离的信息;M0为试件真实磁矩。
赤道作图法在整个测量和计算过程中会受到仪器、试件结构和环境等因素的影响,本文仅就以下主要方面误差因素进行分析:
3.1 磁强计水平度及相互干扰引起的误差
磁强计是赤道作图法测量磁矩的重要仪器。由图2 可知,赤道作图法一般使用3~4 个磁强计阵列进行数据采集。本文使用英国Bartington 公司的三轴磁通门磁强计作为测试设备,在测量过程中呈水平、线性排布。当多个磁强计传感器组成阵列时,由于磁强计自身带有线圈和电路,相邻的磁强计之间会有干扰;同时,磁强计摆放的水平度变化也会造成测量误差。
在试验过程中,磁强计阵列布置于铝制水平伸杆上,调节伸杆可以控制3 台磁强计之间的位置关系和水平度,而伸杆的上翘和下旋会引起磁强计测量值在三分量上的变化。本文以水平杆y方向为例,按实际情况测试和分析了磁强计水平度0°~10°之间各磁场分量的变化关系,结果如图3 所示。

图3 磁场分量随磁强计水平度的变化Fig. 3 Variation of the magnetic field component against the levelness of magnetometer
由图3 可以看到,随着伸杆下旋夹角的增大,磁场y分量呈余弦函数形式减小,z分量呈正弦函数形式增大,x分量不变。这就会带来磁矩分量的误差,其量级与被测试件的磁矩大小有关。磁测时可利用电子水平仪来保证磁强计的水平度。
磁强计之间距离太近会相互干扰,引起数据波动,导致计算误差增大。如图4 所示,以两磁强计相对平行、相距100 mm 布局时磁强计A 的测量数据为基准,滑动磁强计B 向磁强计A 靠近,每次移动1 mm,观察和记录磁强计A 测量数值的变化,找到两磁强计间干扰最小的位置,记录两者中心间距D,测试结果见图5。

图4 磁强计干扰测试现场Fig. 4 Magnetometer interference test site
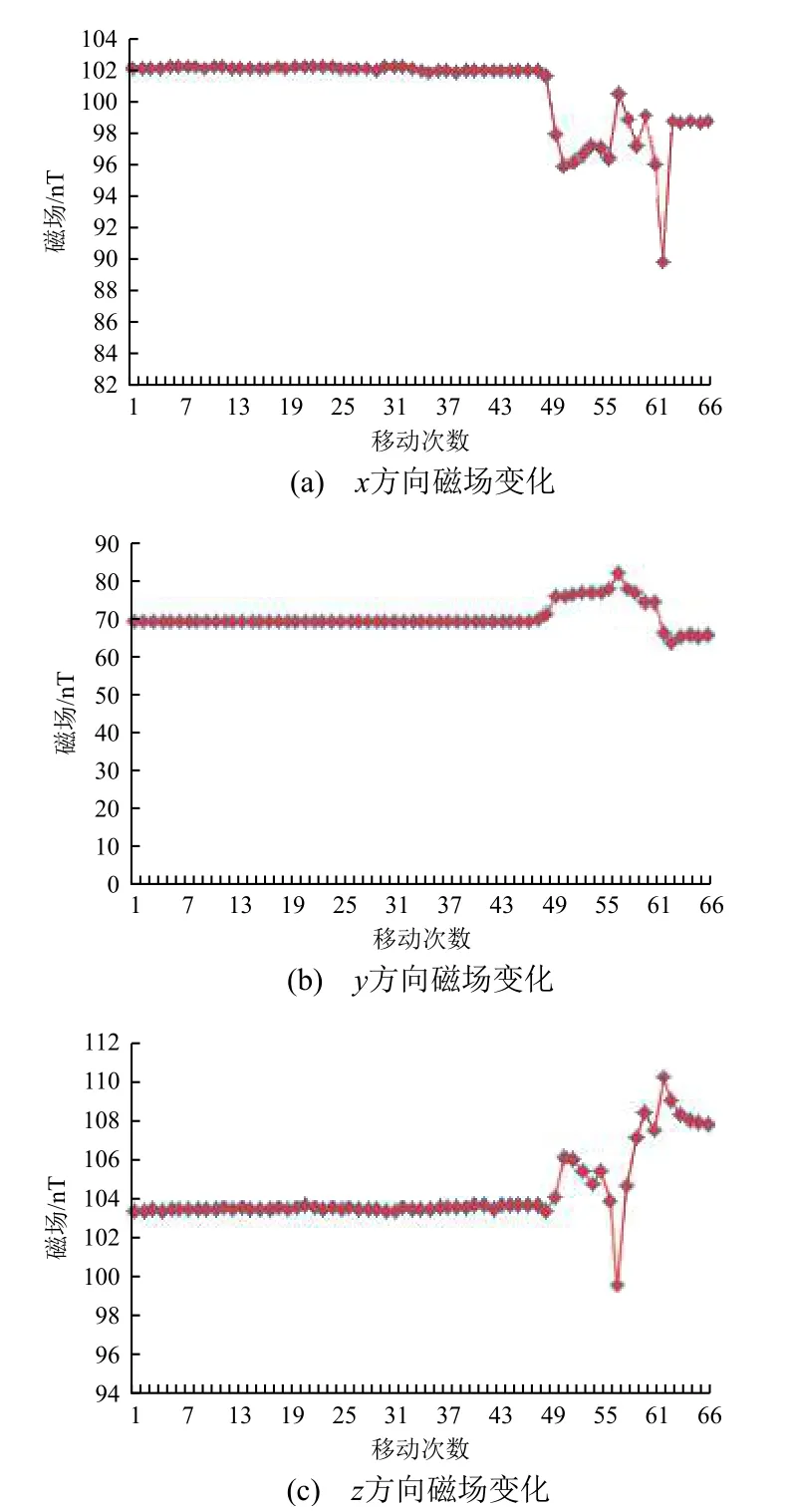
图5 磁强计A 的受扰测试结果Fig. 5 Interference test result of the magnetometer A
从图5 给出的试验测试数据可以看出,当磁强计B 向磁强计A 移动46 次时,后者的读数开始受到影响,移动61 次时两磁强计相贴,此后读数趋于平稳。这说明两磁强计间距D≤54 mm 时会产生相互干扰,在试验过程中应保证磁强计间距大于这个距离。
3.2 磁偏心引起的误差
赤道作图法中的测量距离是指磁强计探头中心到试件几何中心的距离,而卫星构型复杂,磁化不均匀,具有一定的体积,导致其磁心与几何中心存在一定的偏差,即偏心距d。本文利用数值模拟的方法,随机生成不同方向和大小(≤1 A·m2)的磁源矢量序列,1 号磁强计探头中心与试件几何中心的距离r1设置为1 m,磁强计间距严格按照行业标准[9]设定,在不同偏心距下的磁矩计算误差如图6所示。可以看出,不同偏心距引起的磁矩计算误差不同,偏心矩超出r1的1/2 后,误差开始变大。
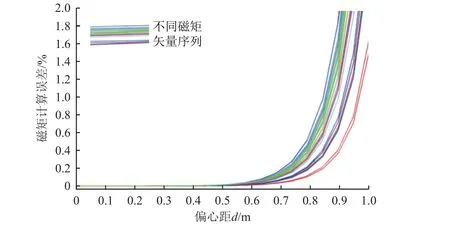
图6 不同磁矢量在不同偏心距下的磁矩计算误差Fig. 6 Calculation error of magnetic moment of different magnetic vectors under different eccentric distances
为进一步了解偏心距对磁矩测量的影响,观测偏心距为0.7 m 时的磁矩误差等势面,如图7 所示。可以看出,在同样的偏心位置,磁矩模拟计算误差容易受到磁矩方向的影响,磁矢指向垂直方向z时,误差最大可达22%;磁矢指向水平方向x时,误差只有2%。
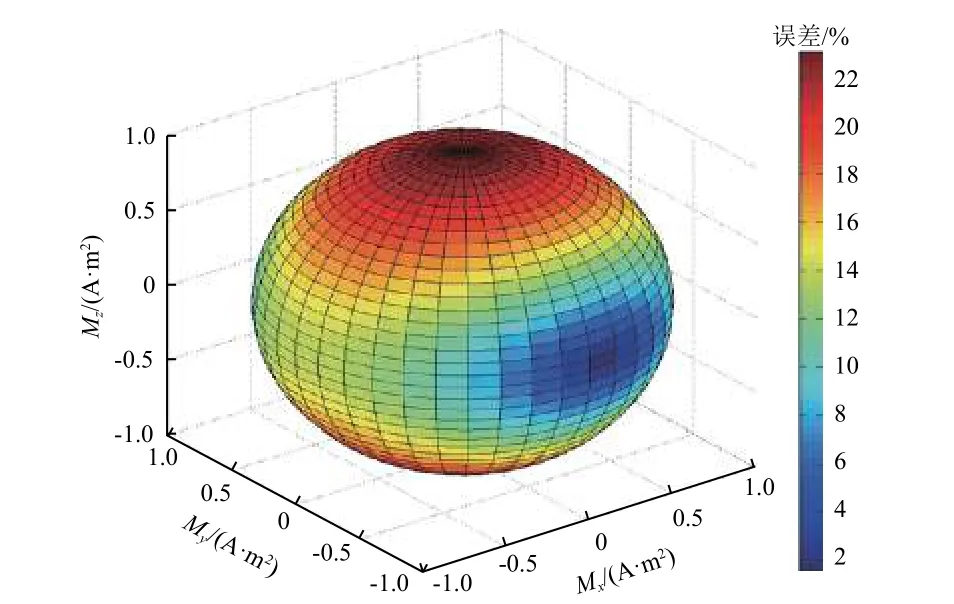
图7 偏心距为0.7 m 时的磁矩误差Fig. 7 Magnetic moment error for eccentric distance of 0.7 m
计算磁矩误差在10%范围内的偏心距,结果如图8 所示。可以看出,设定误差阈值10%,磁矢指向垂直方向z时,偏心距为0.65 m;磁矢指向水平方向x、y时,偏心距为0.85 m。这说明磁矢垂直方向对偏心距最敏感,水平方向次之。
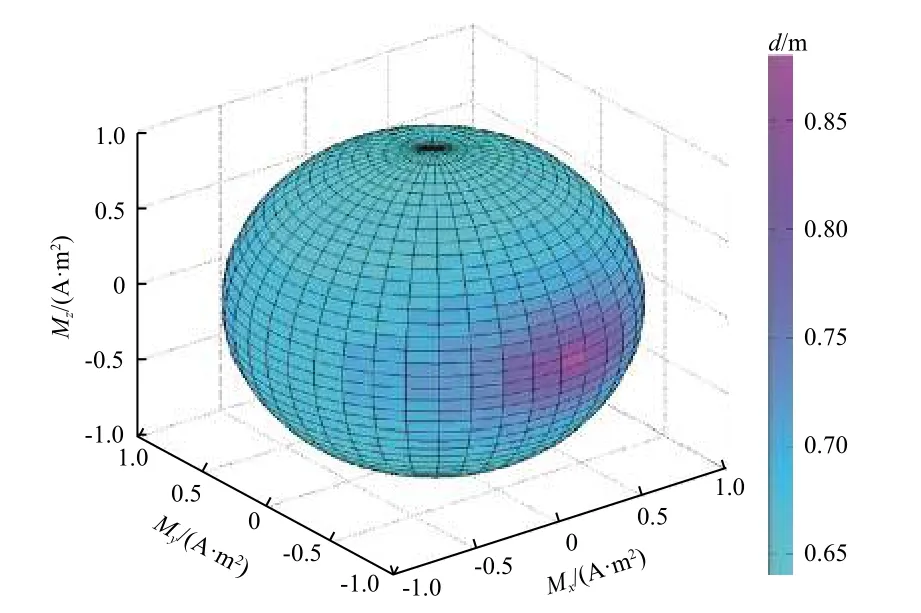
图8 磁矩误差10%对应的偏心距Fig. 8 Eccentric distance corresponsive to magnetic moment error of 10%
选取0.5 A·m2的标准磁块,r1设为1 m,按不同偏心距计算标量磁矩,结果见图9。可以看到,磁矩计算误差在偏心距达到0.5 m 后随偏心距的增加而增大,且垂直方向计算误差随偏心距增加的程度大于水平方向。
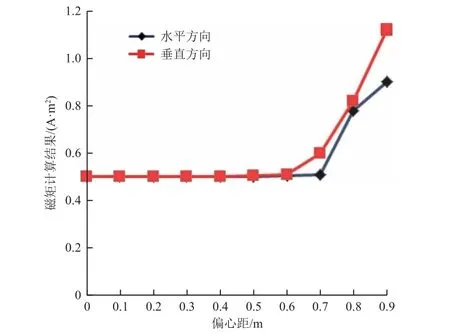
图9 不同偏心距下的磁矩计算误差Fig. 9 Calculation error of magnetic moment for different eccentric distances
另外,本文研究了偏心距对磁场三分量测量曲线尖锐程度的影响。将1.0 A·m2的标准磁块放置于30 cm 处,调节偏心距,以x分量为例,磁场测量结果如图10 所示。
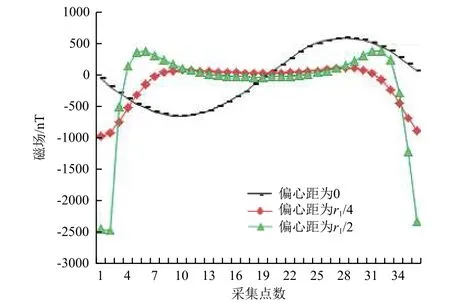
图10 不同偏心距下的x 方向磁场测量曲线Fig. 10 Magnetic field in x direction with different eccentric distances
可以看到,当偏心距为0 时,数据曲线较为平缓,呈正弦形式;当偏心距达到r1的1/2 时,曲线呈现较为尖锐的形状。其他2 个分量的磁场数据也有同样的趋势,说明可根据磁场采集图形初步判断偏心距的大小。
3.3 背景磁场干扰引起的误差
实验室周边环境复杂,在试验过程中常常会有地磁场波动或者外部磁源移动,引起测量数据的波动,增加磁矩计算误差。设测量距离固定为1 m,选取3 种标准磁块(0.1 A·m2、0.5 A·m2、1.0 A·m2),背景干扰由10 nT 增加到100 nT,利用赤道作图法模拟磁矩计算误差,结果见图11。可以看出,测量距离一定时,背景干扰引起的磁矩计算误差线性增加,其量级与背景干扰成正比。
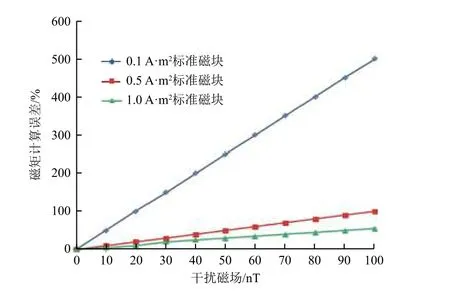
图11 背景干扰引起的误差Fig. 11 Error caused by background interference
本文提出近远场梯度差分的方法来降低背景干扰。设某方向干扰磁场为B0,近场磁强计对应方向测量数据为B1+i,远场磁强计对应方向测量数据为B2+i,其中i=0, 1, 2, 3, …,则每次磁场数据采集间隔之间的干扰为
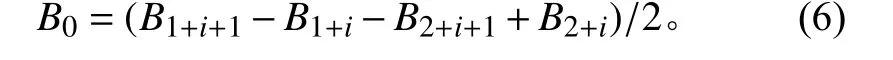
利用式(6)对实测数据进行去干扰处理,结果见图12。
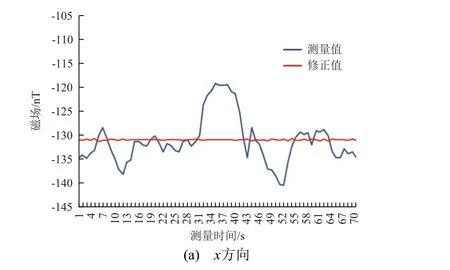
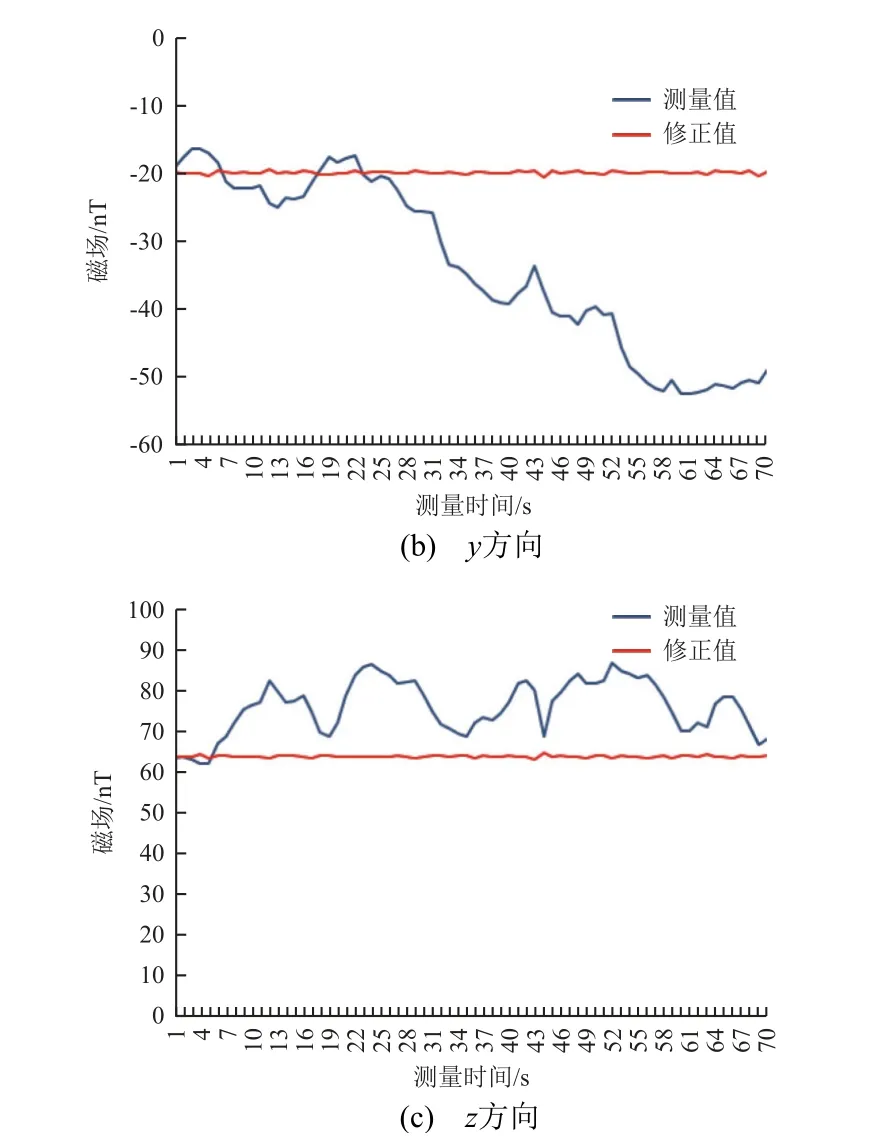
图12 去除背景磁场干扰结果Fig. 12 Magnetic field result after eliminating background interference
由图12 可以看到:起初在白天复杂环境下,测量数据波动较大;使用本文算法去除干扰后,x分量峰-峰值由20.91 nT 降至2.14 nT,降低1 个数量级;y分量峰-峰值由35.93 nT 降至0.38 nT,降低2 个数量级;z分量峰-峰值由24.73 nT 降至0.98 nT,降低2 个数量级,3 个方向的背景磁场干扰均得到有效控制。
3.4 其他误差
除3.1~3.3 节所述影响因素外,其他会引起磁测误差的因素及应对措施包括:转台旋转角度误差对磁矩计算结果有一定影响,可通过在无磁转台上安装高精度无磁角编码器来有效降低该因素的影响;由磁强计受环境温度变化对磁矩测量产生的影响通常不大,除极端异常温差环境外该误差因素可以忽略;通电线路会引发周围磁场的变化,其影响量级与电流大小、导线形状和试件自身磁矩大小有密切关系,可通过导线屏蔽、双绞、对称抵消等方法去除此类干扰。
4 试验验证
本章根据第3 章的误差分析,综合使用对应的控制措施来降低赤道作图法的测量和计算误差。试验验证流程如下:
4.1 测试系统搭建
整个测试系统包括无磁转台(含角编码器)、无磁支架、水平伸杆、标准磁块、磁强计(量程0~100 000 nT,分辨率0.1 nT)和数据采集系统(数据传输电缆均使用双绞线),如图13 所示。

图13 赤道作图法磁矩测试系统Fig. 13 Magnetic toque testing system set for equatorial mapping method
4.2 验证结果
测试样本为0.2 A·m2、0.5 A·m2、1.0 A·m2标准磁块(顺序编号为磁块1~3),测试距离r1为0.5~1.2 m,验证结果详见表1。从试验验证结果来看,在应用误差控制方法之后,磁矩测量结果的误差较小,可控制在3%以内。
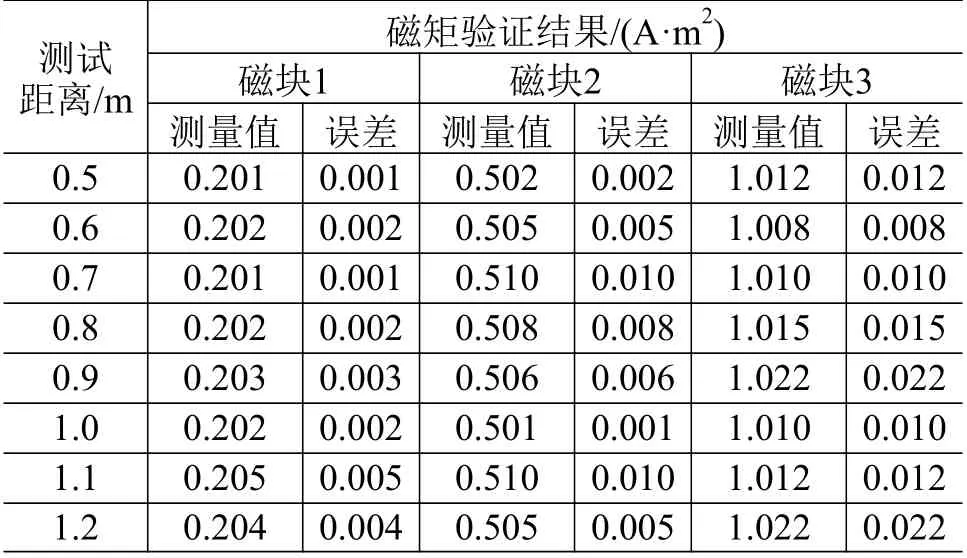
表1 赤道作图法磁矩测试试验验证结果Table 1 Verification result for magnetic toque testing by equatorial mapping method
5 结束语
本文研究了赤道作图法在样本产品磁矩测试中的部分误差来源,并提出对应的控制措施,包括:
1)两相邻磁强计的间距应控制在一定范围(本文为54 mm 以上),以减小磁强计互相干扰带来的测量误差;
2)被测磁体的磁偏心距应尽量小于1 号磁强计探头中心与试件几何中心距离的1/2;
3)磁强计与被测物体磁矩方向尽量保持在同一水平面内;
4)利用近远场梯度差分法消除背景磁场干扰;
5)安装无磁角编码器减小角度误差;
6)数据采集系统电缆使用屏蔽双绞线减小电流磁场干扰。
通过上述措施和方法,以标准磁块为被测试件,用赤道作图法测量和计算出的磁矩的相对误差可控制在3%以内。
本文所述研究内容对卫星及其部组件的磁矩测量和计算有一定参考意义,后续将针对复杂卫星模型进一步研究探索卫星磁矩测量方法,提高卫星磁矩测量和计算精度。
