亚高斯随机矩阵的稀疏恢复

宋儒瑛,郑珂,关晋瑞

(太原师范学院数学系,山西 晋中 030619)

1 引言

压缩感知是一种寻找欠定线性系统的稀疏解的技术.近些年来,该领域进行了大量的研究.Donoho和Cand`es及Tao[1-2]的开创性工作成功地解决了这些问题,即通过研究m×N测量矩阵A以及恢复算法,找到压缩感知模型y=Ax的最稀疏解.选择合适矩阵是利用了概率论的方法,得出结论:大多数随机选择的矩阵可以有效地重建稀疏向量.重建问题在于解决可计算的凸优化问题

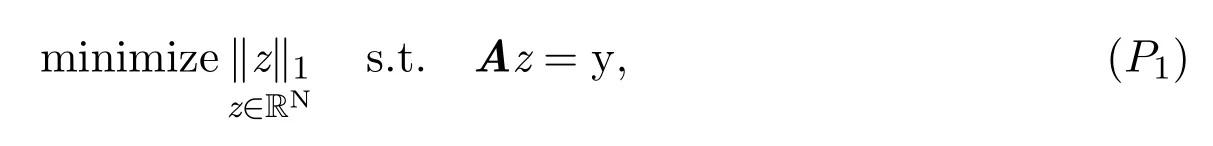
来取代NP-困难非凸优化问题

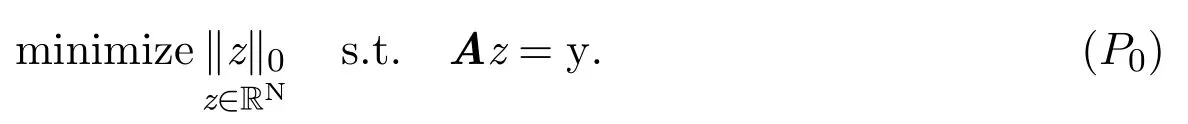
时具有第k阶限制等距性质.其中满足不等式(1)的最小常数用δk表示,并称其为矩阵A的最小限制等距常数,详见文献[4].对于满足集中不等式的随机矩阵,由限制等距性质(1)以及测量值满足m≥csln(eN/s)的条件下,推导出ℓ1最小化稀疏恢复是可能的,文献[5]有相关证明.当随机矩阵是亚高斯随机矩阵时,详见文献[6].

对于亚高斯随机矩阵,经典的限制等距性质可以做出一些相应的修正.取限制等距性质中内范数为ℓ2范数,外范数为文献[7]中涉及到的外部范数,即

其中

如果每个νi,j的第一个绝对矩是有限的,那么很容易验证出现在文献[8-10]中的这种表达式定义了RN上的范数.该外部范数依赖于概率分布构成了研究的新颖性.由此得到的修正限制等距性质如下:

一个项ai,j是根据中心概率测度νi,j分布的随机矩阵A∈Rm×N,它的最小限制等距常数δ∈(0,1),使得

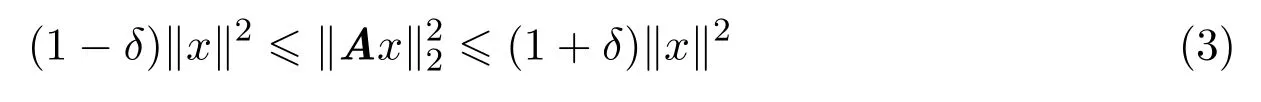
成立,其中k稀疏向量x∈RN.

本文在第一部分中介绍了相关的预备知识,第二部分建立了关于范数(2)的集中不等式,在第三部分中证明了修正了的限制等距常数是足够小的,第四部分中证明了测量矩阵满足修正限制等距性质(3),相对于欧几里得范数而言,可以通过ℓ1-最小化进行稀疏恢复.第五部分结合前面的结果得出主要定理.第六部分运用实验验证了定理结果的正确性.为了解释的清楚,可以选择只处理从完美测量中恢复精确稀疏向量的问题.

2 预备知识

首先从亚高斯随机变量的定义以及它的等价性条件开始.

3 亚高斯尾衰减

4 修正限制等距性质

5 稀疏恢复

6 主要定理

7 实例验证

图1 不同稀疏度的信号重建

根据图1可知,随着测量值的不断增大,信号成功恢复的概率也不断增大,那么根据常数C2的大小可知,本文所证明的定理中测量值的条件足以使得信号进行稀疏恢复,定理得以验证.

8 结束语

本文通过应用依赖于概率分布的范数,证明了一个具有独立亚高斯随机系数的m×N欠定线性方程组满足限制等距性质时,在最优条件m≥csln(eN/s)下,系统的s稀疏解可以通过ℓ1最小化得到.在Simon Foucart,Ming-Jun Lai等人对于预高斯随机矩阵稀疏恢复的基础上,对亚高斯随机矩阵稀疏恢复进行了证明,并且将文献[11]限制等距性质中ℓ2范数用依赖于概率分布的范数取代,得出了新的结果.