µ-b方程族柯西问题的不适定性

严可欣,陈涵,付英

(1.宁波大学数学与统计学院,浙江 宁波 315211;2.西北大学数学学院,陕西 西安 710127)

1 引言

考虑如下周期偏微分方程的柯西问题:

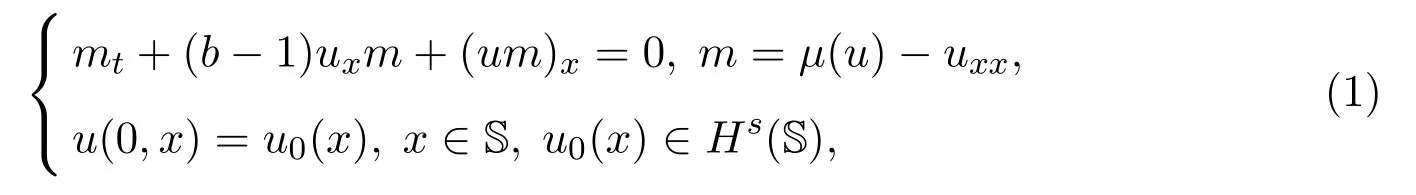
在b>1情形下的不适定性,其中u(t,x)是实值空间周期函数,S代表 R2上的单位圆,µ(u):= ∫Su(t,x)dx表示u在 S上的平均值.柯西问题 (1)中的第一个方程是µ-Camassa-Holm(µ-CH)方程和µ-Degasperis-Procesi(µ-DP)方程的一个混合方程,被称为µ-b方程族.

当b=2时,µ-b方程族变成µ-Hunter-Saxton方程(现在通常被称为µ-CH方程):

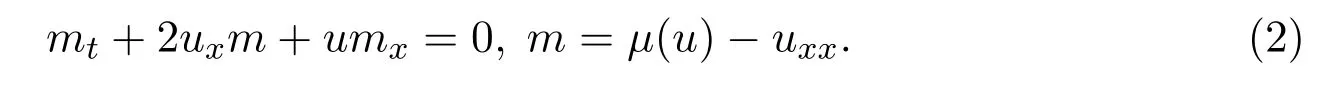
该方程是著名的CH方程[1-2]和Hunter-Saxton[3]方程的“中间”方程.它是由Khesin,Lenells和Misiołlek[4]首先提出的,它描述了具有外部磁场和自相互作用的液晶中旋转子的演化过程.关于µ-CH方程的几何性质,可积性,尖峰孤子解的存在性和稳定性,解的爆破行为,局部和全局适定性等可见文献[4-6].

当b=3时,µ-b方程族变成µ-DP方程:

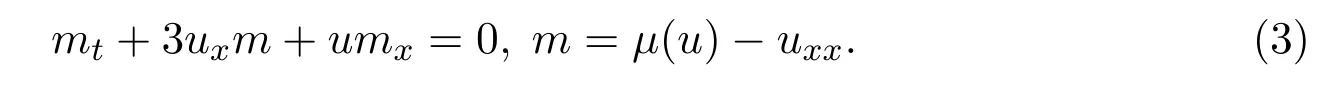
µ-DP 方程是由 Lenells,Misiołlek和 Ti˘glay引入的[7].作为 DP 方程[8]和 Burgers方程[9]的“中间”方程,µ-DP方程可以视为圆S=R/Z的所有光滑且保向的微分同胚的Fréchet李群 Diff∞(S)上的右不变仿射联络∇的测地线流.关于µ-DP方程的其他几何性质,可积性,局部适定性,尖峰孤子解和冲击波解的存在性,解的爆破和波浪破碎等结果可参考文献[6-7].

µ-b方程族是b方程族的一个周期形式的推广,它是由Lenells,Misiołlek和Ti˘glay引入的[7].µ-b方程族解对初值的不一致依赖问题在文献 [10]中被讨论.值得一提的是,从文献 [7]的定理5.5可以知道,当s>3/2时,µ-b方程族的柯西问题存在唯一解u∈C((−T,T),Hs(S))∩C1((−T,T),Hs−1(S)),且解对初值是连续依赖的.那么一个自然的问题是:当s<3/2时,µ-b方程族是否适定?

关于多种方程定解问题的不适定性已有许多工作.例如,2008年,在范数膨胀的意义下,Bourgain和Pavlovic[11]证明了三维Navier-Stokes方程在贝索夫空间的不适定性.2014年,Himonas,Holliman和Grayshan[12]研究了DP方程在索伯列夫空间Hs(R)与Hs(T)中的不适定性.2016年,Himonas,Grayshan和 Holliman[13]研究了b方程族在b>1时,在线上和圆环上的不适定性.至于b方程族在b<1情形下的不适定性,它是由Novruzov[14]在2021年研究的.关于 Novikov方程,ab方程族,修正CH方程,广义修正CH方程的不适定性研究的结果可参考文献[15-18].受文献 [12-13]的启发,本文研究的是当s<3/2,b>1时,µ-b方程族的柯西问题在空间Hs(S)中的不适定性.主要结论如下:

定理 1.1当b>1,s<3/2时,则µ-b方程族的柯西问题 (1)在索伯列夫空间Hs(S)中,在哈达玛意义下是不适定的.具体地讲,当

时,解的范数发生膨胀;当 (b,s)∈{(1

2 预备知识

为了证明主要结论,给出如下基本定义和引理.

定义 2.1[12-13]称µ-b方程族在索伯列夫空间Hs(S)中,在哈达玛意义下是适定的,如果µ-b方程族满足以下三个条件:

3 主要定理的证明