基于流体体积模型的叶轮宽径比对水车性能的影响

李可欣，郑源，胡雪原

(河海大学能源与电气学院，江苏 南京 211100)

自19世纪50年代以来，中国水力发电技术都把重点放在依赖水头的传统水轮机的性能和效率上，而没有更多关注微水头下水流中的能量.实际上，中国河流众多，微水头及超低水头发电蕴含的能量巨大.在古代，人们利用水车作为磨坊等生产单位的动力来源，随着人们对可再生资源的重新认识和偏远地区智能发电需求的提升，传统水车发电凭借其易于安装、环保等特点再一次进入人们的视野.

随着超低水资源开发利用的迫切需求，为了研究水车的工作性能，国内外一些学者已进行了数值模拟和试验研究.赵梦晌等[1]对不同叶片数的水车在不同转速下进行非定常模拟.结果表明:三叶片水车效率区最为宽广.HUNG等[2]对水车式潮汐水轮机进行了不同叶片数和不同叶片形状在不同叶尖速比TSR下的比较，数值结果表明，十叶片和直叶型水车的效率最高.此外，二十叶片和弯叶型在所有TSR情况下的性能均低于其他类型.NGUYEN等[3-4]采用试验和数值结合的方法对潮汐能水轮发电机组的性能和流场进行了分析.结果表明，水车有效地运行在小叶尖速比范围内，在那里产生最高的水力效率；在TSR=0.94时，六叶单排水车的性能最好.WARJITO等[5]采用解析法和数值方法，建立了一个确定应使用多少叶片的方程，并考察了水动能对能量转换过程的影响.结果表明，八叶水车在进气速度为1 m/s(效率为45.58%)和5 m/s(效率为13.84%)时效率最高.VIDALI等[6]在实验室试验通道中对胸射式水车进行研究，得到的数据表明，在旋转速度约为失控速度的60%时，胸射式水车的最大效率可达75%左右.JASA等[7]测试了3种不同叶片形式的模型水轮机，结果表明，在螺旋桨和弯桨之间，三角形模型的效率最高.PAUDEL等[8]研制了一种实验室规模的柔性橡胶叶片水轮，研究了沟道宽度对水轮性能的影响.结果表明，减小通道宽度后，功率输出和效率均有显著提高.PUJOL等[9]研究表明，水平轴水车可获得高达81%的水力效率.当改变净可用水头时，如此高的水力效率不会发生实质性的变化.YAN等[10]利用计算流体力学(CFD)方法研究了浸没叶片深度对直叶片下冲式水轮机的影响.仿真结果表明，最佳浸没深度为40 mm.此外，还有一些学者也对水车性能与优化进行了分析.但他们大多数都集中于分析叶片个数和形式等因素对水车性能的影响，而对于叶轮宽径比对水车性能的影响尚未涉及.文中将从该角度进行数值模拟与分析，以期对水车的结构设计起到指导作用.

1 模型及数值计算方法

1.1 模型的建立及网格划分

以江西某河流中的水车为研究对象，水车安装处河流宽度为11.4 m.根据实际情况，采用1个具有大尺寸、低角速度的叶轮，能够使水生生物脱离危险，同时提供了良好的泥沙通道，可以使垃圾更容易漂浮.

根据文献[1]的指导，三叶片水车效率区最为宽广，故将水车叶片数初步拟定为3个；又据参考文献[2]中提出的直叶型水车效率最高，选取直叶型叶片，建立水车全流道模型，其俯视图如图1所示.

图1 几何模型及其俯视图

水车叶轮直径D初步设计为2.8 m，轮毂半径r取0.16 m，叶片长度为1.24 m，叶片厚度为0.11 m；流道宽度b1为11.4 m，流道长度L取7D为19.6 m，流道高度H取2D为5.6 m；液面高度h为2.8 m.现将叶片宽度b2与叶轮直径D的比值b2/D定义为一参变量，探究水车在不同叶轮宽径比下性能的变化.由于叶片宽度不能超过挡水墙间距，故叶轮宽径比应小于4.07.为使水车充分过流且出力不应过小，叶轮宽径比在2～4为宜.

运用ICEM CFD软件进行网格划分，由于叶轮体是关键部位且形状规则，旋转域采用结构化网格，流道域采用自适应性强的非结构化网格，并对流道域边界线进行局部加密.为了保证计算的精度和效率，对计算域网格进行网格无关性验证，最终将网格数确定在300万左右，网格质量均在0.33以上.计算域网格划分示意图及核心转动区域网格划分分别如图2,3所示.

图2 全流道整体网格划分

图3 旋转域网格划分

1.2 计算方法

VOF模型是建立在2种或者多种流体(或相)不互相混合的前提下，采用一种成熟的界面跟踪方法处理界面拓扑复杂的两相流.当需要得到一种或多种互不相融流体交界面时常采用此方法.

由于胸射式水车运行环境为明渠无压流动，带有气液交界面，故采用VOF模型、隐式插值格式.采用滑移网格模型，滑移网格在计算中叶轮体部分的网格会实际转动.在该模型中，不同的流体组分共用一套动量方程，计算时在全流场的每个计算单元内都记录下各流体组分所占的体积率，其连续性方程及动量方程为

(1)

(2)

式中：p为静压；τij为应力张量；xi,xj分别为位置矢量；vi为平均速度；ui,uj均为平均相对速度分量；gi和Fi分别为i方向上的重力体积力和外部体积力(如离散相互作用产生的升力)，Fi包含其他模型相关源项，如多孔介质和自定义源项.

数值模拟计算选用SSTk-ω湍流模型[11]，采用非定常计算，压力-速度耦合采用PISO格式进行求解，压力采用body force weighted格式进行空间离散，可以保证法向速度通过单元面的连续性.采用改进的高分辨率界面捕获(HRIC)方案计算体积分数.前5个周期设置为叶片每旋转3°为1个时间步长，后3个周期设置为叶片每旋转1°为1个时间步长，取后2个周期的计算数据进行分析.

1.3 边界条件设置

水车正面运行示意图如图4所示，其中红色表示气体，蓝色表示液体.

地震高振幅异常反射表明有气体存在[22]。小断层也表现为沿断层面的高振幅反射。URU界面之上没有观察到高振幅反射，表明向上迁移的气体圈闭在此或者在URU界面以下。晚侏罗纪Hekkingen地层可能是研究区浅层气体的来源，深部气体对渗漏可能也有贡献作用；图8b展示了来自Loppa高地的重大断裂区域，断层面上有高振幅反射，暗示有气体的存在。少量的断层延伸至海底，这些断层的终止也与海底的小凹陷相一致。

图4 水车运行示意图

进口边界条件设置为分离相速度进口，给定水流流速为2.5 m/s，速度方向垂直于进口边界；气体流速为0，速度方向垂直于进口边界；湍流强度为1%，自由液面高度为0.

出口边界条件设置为压力出口，出口压力与大气压力相同；湍流强度为1%，自由液面高度为0，流道底部高度为-2.8 m.

叶轮转速设置为7 r/min，转动方向从前向后看为逆时针旋转.叶片、轮毂及所有壁面均设置为无滑移壁面边界条件；旋转域与流道域的接触面设为INTERFACE类型，以保证计算过程中两区域之间能量传递.流道域上表面采用对称边界条件.计算精度设置为10-5.

1.4 水车功率性能分析

为了研究不同工况下胸射式水车的流动特性，采用量纲为一的参数叶尖速比λ[1]来描述水车的转速，λ定义为

(3)

式中：ω为水车叶轮旋转的角速度，rad/s；v为水相流速，m/s;R为叶轮半径,m.

采用功率系数Cp[1]对水车的功率性能进行评价，即

(4)

式中：T为水车叶片相对于叶轮中心线的转矩，N·m；ρ为水的密度，kg/m3；A为叶轮浸没水中的面积，m2.

图5为不同叶轮宽径比下的功率特性曲线.不同叶轮宽径比在不同情况下功率特性呈现出先增大后减小的相似变化趋势，但增大和减小幅度略有不同，最优功率系数均在λ为0.410 5(即水车转速n=7 r/min)时达到，且叶轮宽径比为4.00(b2=11.2 m)时，转矩变化正负值同时存在，这种情况的出现可能是因为叶轮宽度过大，使得叶片间残余水量过多，从而导致水车反向旋转，此种结构下水车已不能正常工作；当叶轮宽径比为3.93(b2=11.0 m)时，功率呈上升趋势直到λ为0.410 5(n=7 r/min)时达到最大功率系数42.24%，而后下降直到λ为0.469 1(n=8 r/min)；当λ为0.527 8(n=9 r/min)时，5种结构下的功率系数皆为负值，这表明在此转速下水车不能正常运行.叶轮宽径比为3.93的高效区较为宽广，叶轮宽径比为3.79次之，叶轮宽径比为2.14的高效区最小.

图5 不同叶轮宽径比下的功率特性曲线

由于水车在河流中运行，根据流域气象条件的差异，存在枯水期、平水期与丰水期，各时期流量变化将导致固定流道的流速发生变化.为了探究水车在不同运行条件下的性能，除以上运行在平水期(v=2.5 m/s)的计算外，文中还计算了不同叶轮宽径比的水车运行在枯水期(v=1.5 m/s)、丰水期(v=3.5 m/s)时的最优功率系数，如图6所示.

图6 不同流速下最优功率系数随叶轮宽径比变化曲线

结果表明，3种入口速度下功率系数的变化呈相同趋势，均随着叶轮宽径比的增大而增大，在叶轮宽径比为3.93(b2=11.0 m)时达到最大，最大功率系数分别为42.24%,24.99%和15.39%.叶轮宽径比小于3.79(b2=10.0 m)时Cp增长速度较快，而后增长较为缓慢.入口速度为2.5 m/s时，同一叶轮宽径比下Cp最大，远大于入口速度为3.5, 1.5 m/s时，且入口速度为1.5 m/s时同一水平下Cp最小.水流速度较小时，叶片所捕获的能量较少；而水流速度过大时，叶片对水流的阻塞效应同时增强.由此可见，胸射式水车在枯水期与丰水期运行时效率均会有所下降，这2种工况均不利于水车稳定、高效运行.

由上述分析可知，不同叶轮宽径比的水车在λ=0.410 5，v=2.5 m/s时运行效率最高，即最优转速为7 r/min，以下分析将在n=7 r/min条件下展开.

1.5 水车流场水体积分数分析

图7为在最优转速为7 r/min时，叶轮宽径比分别为3.93，3.79，3.57，2.86，2.14这5种情况下水车在旋转相同角度时刻下的水体积分数W云图.

图7表明，随着叶轮宽径比的增大，流道上、下游水位差逐渐增大，这是由于叶轮宽径比的增大使得流道的阻塞效应增强，叶轮宽径比为3.93时平均水位差达到了2.89 m，相比于2.14的宽径比，平均水位差增加了1.37 m.水流的一部分动能转化为上、下游水位的势能，使得水车捕获水流能量的能力减弱.同时，水位差波动幅度过大会对水车出力和工作的稳定性产生不利影响.叶轮宽径比为3.79和叶轮宽径比为3.93的水车上、下游水位波动剧烈，水位差相比于其他2种叶轮宽径比过大，因此会产生涡流现象，随着涡团扩散和级联散列，相同工况下叶轮宽径比为2.14的水车上、下游涡黏度相差较大，下游涡黏度影响范围较小；而叶轮宽径比为3.93的水车上、下游涡黏度较为平均，影响范围较大.在转速为7 r/min时，叶轮宽径比为2.14和叶轮宽径比为3.93的水车上、下游涡黏度云图如图8所示，图中e为涡黏度.

图7 不同叶轮宽径比下的水体积分数云图

图8 叶轮宽径比为2.14和3.93时的涡黏度云图

1.6 转矩分析

图9为不同叶轮宽径比水车在转速为7 r/min时，同一时刻下叶片转动2个周期的扭矩变化图.

图9 不同叶轮宽径比的水车旋转2个周期转矩的变化

图10 平均转矩随水车叶轮宽径比的变化

同时，对比了不同叶轮宽径比的水车运行在枯水期(流速为1.5 m/s)的转矩变化，如图11所示.

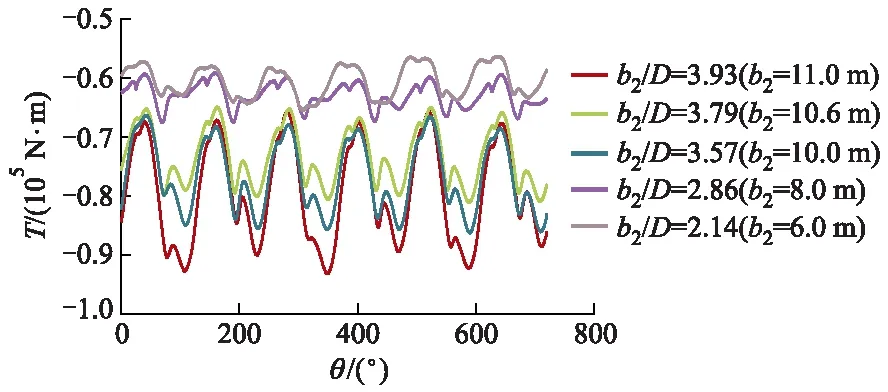
图11 不同叶轮宽径比下转速为1.5 m/s时水车旋转2个周期转矩的变化

在水流流速为1.5 m/s，转速为7 r/min时，转矩总体变化规律与水流流速为2.5 m/s时相同，呈周期性变化，每个周期变化120°.平均转矩随着叶轮宽径比的增大而增大，叶轮宽径比为3.93(b2=11.0 m)时平均转矩最大为-0.6×105N·m，且转矩变化范围最大，出力最大.在枯水期工况下，水流对叶片的冲击作用明显减弱，当2个叶片浸入水中旋转运动时，两叶片间会出现回流现象，使叶片受到周期性不平衡力的作用，导致小范围的转矩回升.这种情况可能会导致水车运行不稳定且对叶片有一定的疲劳损伤.

1.7 叶片表面周围的流动方式

图12为不同叶轮宽径比下的压力轮廓，比较了非定常下同一工况叶轮转过相同的角度时刻下各叶轮宽径比下的压力p等值线.从模拟结果可以清楚地看出，未浸入水中的两叶片间压力随着叶轮宽径比的增加逐渐增大.这是由于叶轮宽径比的增大使得未浸入水中的两叶片间残余水量增多，增大了其对叶片的挤压作用.随着叶轮宽径比的增大，总体上浸水叶片压力沿着叶片延伸方向从轴线向外逐渐升高，在叶片边缘处达到最大.叶尖处正面压力峰值随着叶轮宽径比的增大而增大，背面压力峰值随着叶轮宽径比的增大逐渐减小.在叶轮宽径比为3.93时叶尖处正面压力最大，且叶片前后表面压力差达到最大，提高了叶片做功的能力，增大了水车的出力，形成了更高的发电量.

图12 不同叶轮宽径比下的压力轮廓

2 结 论

1) 胸射式水车功率系数Cp随叶尖速比λ先增大后减小，最优转速为7 r/min；叶轮宽径比为3.93(b2=11.0 m)的胸射式水车效率较高，且最大Cp随着叶轮宽径比的增大而增大，但当叶轮宽径比为4.00(b2=11.2 m)时，转矩变化正负值同时存在，水车几乎不能正常运行.几种叶轮宽径比的水车均在入口速度为2.5 m/s时达到最大.此时，叶轮宽径比为3.93的水车在λ=0.410 5下达到最高效率42.24%.在相同工况下，为了提高水车的出力，选用宽径比为3.93的叶轮为宜.

2) 同一工况下，叶轮宽径比为3.79和叶轮宽径比为3.93的水车上、下游水位波动较为剧烈，叶轮宽径比为2.14的水车水位差波动最小.叶轮宽径比增大使得流道的阻塞效应增强，上、下游水位差增大，出现明显涡流现象.

3) 同一工况下，不同宽径比的水车叶轮叶片转矩呈现同一周期性变化规律，叶轮宽径比为3.93的水车叶片转矩变化幅度最大且平均转矩最大.当水车处在枯水期运行时，叶片运动过程中浸入水中的两叶片间会出现回流现象，使得转矩有小范围的极值出现.这种情况会导致水车运行不稳定，且对叶片有一定的疲劳损伤.

4) 同一工况下，未浸入水中的两叶片间压力随叶轮宽径比增大而增大，增大了水流对叶片的挤压作用.叶尖处正面压力峰值随叶轮宽径比的增大而增大，背面压力峰值随叶轮宽径比的增大而减小；几种宽径比的水车叶片均在叶尖处正面压力达到最大，且叶轮宽径比为3.93的水车浸水叶片正、背面压力差最大，提高了叶片的做功能力.