氮化硅微波高温介电函数深度学习分子动力学模拟

李志强 谭晓瑜 段忻磊 张敬义 杨家跃†

1) (山东大学前沿交叉科学青岛研究院,光-热辐射研究中心,青岛 266237)

2) (山东大学能源与动力工程学院,济南 250061)

3) (航天材料及工艺研究所,先进功能复合材料技术重点实验室,北京 100076)

氮化硅(β-Si3N4)是当下最具应用前景的热透波材料,其基础物性高温介电函数的精准测量对加快氮化硅基热透波材料的设计,解决高超声速飞行器“黑障”问题具有重要意义.本文以第一性原理数据为基本输入,基于深度神经网络训练得到深度学习势,然后运用深度学习分子动力学方法计算了氮化硅高温微波介电函数.与传统经验势相比,深度学习势的计算结果与实验结果在数量级上保持一致;同时发现,深度学习分子动力学在计算速度方面表现优异.此外,建立了氮化硅弛豫时间温度依变性的物理模型,揭示了弛豫时间温度依变性规律.本研究通过实现大规模高精度的分子动力学模拟计算了氮化硅高温微波介电函数,为推动氮化硅基材料在高温热透波领域的应用提供了基础数据支撑.

1 引言

飞行器高超声速飞行时经受剧烈的气动加热,表面温度高达700—3000 K,天线罩会出现“黑障”(blackout)[1−3]现象.为避免“黑障”现象影响通信质量,要求热透波材料在高温状态下有极低的介电参数和介电损耗,且在很宽的温度区间内变化幅度小.氮化硅具有优异的高温力学、抗热震性能以及良好的介电特性,已成为一种具有重要应用前景的高温透波材料.然而,由于实验条件的限制,很难在极端高温条件下测量氮化硅的介电性能.另外,飞行器价值不菲,如仅凭实验测量来收集数据参数,成本较高,并且由于高速飞行器回收困难,其原始实验数据的准确性很难保证.鉴于以上技术难点,迫切需要探索一种精确计算氮化硅高温介电参数的理论方法.

当前氮化硅介电特性的研究主要集中在采用实验方法结合电介质理论建立理论模型对高温下氮化硅介电特性进行推算[4,5].理论模型中的关键参数依赖实验测量或经验假设,难以适用于计算热透波材料的高温微波介电函数.分子动力学(molecular dynamics,MD)模拟可从原子尺度准确描述材料的结构演变过程和计算相关物性,是获得电介质理论关键参数的重要手段.研究表明[6−8],基于线性响应理论可将分子动力学模拟计算得到的偶极矩数据用于计算材料介电常数.Afify 等[9]和Cardona 等[10]利用分子动力学模拟研究了水、乙醇、乙二醇以及乙醇胺的微波介电特性,发现极化经验力场更适合用于描述物质的介电特性.由此可知力场是保证MD 模拟准确的重要前提,经验力场是由实验数据和第一性原理数据拟合得到,显然不适用于描述氮化硅高温微波条件下原子间相互作用.机器学习势[11,12]结合AIMD (ab initiomolecular dynamics)方法精度高和MD 方法计算效率快的优点,从求解电子薛定谔方程出发构造原子间相互作用势而无需引入经验模型,为计算氮化硅高温微波介电函数指明了研究方向.

目前常见的机器学习势有高斯近似势[13]、高维神经网络势[14]、矩张量势[15]和深度学习势 (deep learning potential,DLP)[16]等方法.得益于图形处理单元 (graphics processing unit,GPU)的加速计算,DLP 在计算效率和精度方面有更出色的表现.Chen 和Li[17]训练了DLP 用于研究300 K 温度下碳化硅的介电性质,计算结果与实验测量数据吻合良好.然而,应用DLP 研究氮化硅高温介电性质的工作却鲜有报道.

本文利用第一性原理数据训练了DLP,并应用深度学习分子动力学 (deep potential molecular dynamics,DPMD)方法模拟了氮化硅的极化弛豫过程.DLP 由不同条件下氮化硅结构训练,其精度通过比较第一性原理计算结果与预测结果来确定.基于训练的DLP,本文计算了氮化硅的微波高温介电函数,计算结果与实验结果高度吻合.此外,建立了氮化硅弛豫时间温度依变性的数学模型,理解和掌握了弛豫时间随温度的变化规律.

2 模型和方法

本文采用融合了电子结构、机器学习和分子动力学3 种手段的多尺度方法研究了氮化硅的微波高温介电性质,技术路线如图1 所示.首先,进行小规模的AIMD 计算用于采集指定热力学条件下的原子结构信息;其次,以选取原子结构的能量、受力、体系尺寸以及原子位置信息为输入,经深度神经网络 (deep neural network,DNN) 进行训练拟合后得到深度学习势;最后,基于深度学习势进行大规模高精度的分子动力学模拟.

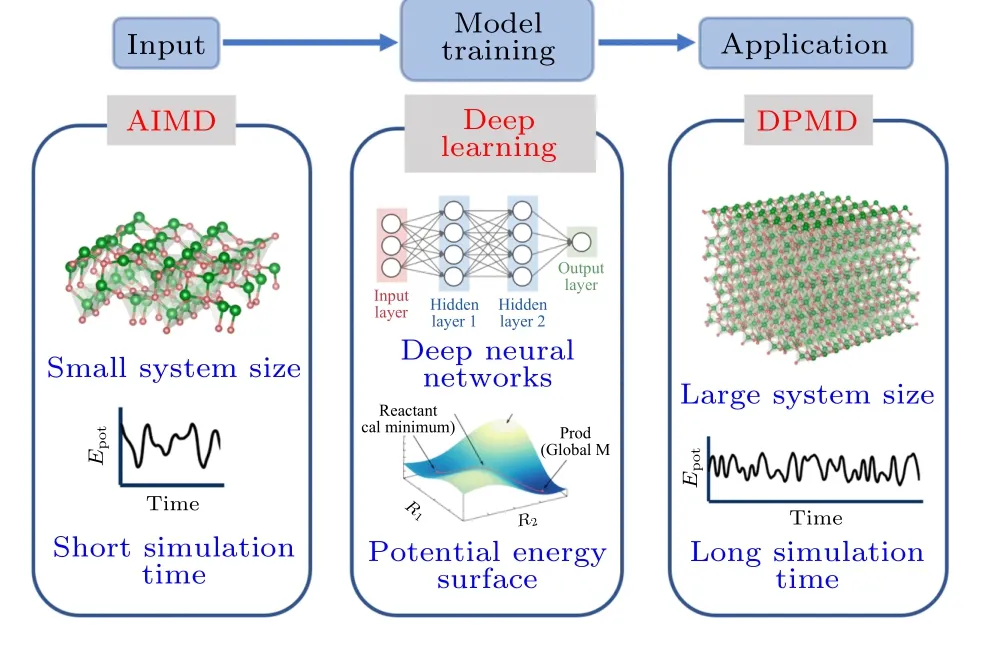
图1 深度学习势训练流程: 主要包含AIMD 计算采样、深度神经网络训练以及深度学习分子动力学模拟三部分Fig.1.DLP training process: AIMD computational sampling,DNN training,and DPMD simulation.

2.1 训练集获取

深度学习势函数的精度取决于训练集的合理性和丰富性.本文使用CP2K[18]软件来生成初始训练构型,初始训练结构的体系原子数目为140,如图2(a)所示.具体过程分为以下3 步: 首先,利用Broyden-Fletcher-Goldfarb-Shanno (BFGS) 算法对β-Si3N4初始结构进行结构优化;其次,整个体系在正则系综(canonical ensemble,NVT)下通过速度标定法进行热力学弛豫平衡,温度设置为300—1000 K (温度间隔为100 K),时间步长为0.5 fs;最后,每个温度条件下各选取一段0.5 ps 的平衡轨迹并记录每个时间步下的体系能量、体系尺寸、原子坐标以及受力信息.混合高斯平面波(Gaussian and plane wave,GPW)[19,20]的密度泛函理论用于评估能量与力: 计算基组选用DZVP-GTHPADE,赝势则分别选用GTH-PADE-q4 (Si)和GTH-PADE-q5 (N),截断能设置为400 Ry,k点网格设置为1×1×1.样本空间的丰富性是决定势函数训练结果好坏的先决条件,因此对AIMD平衡轨迹中的构型进行筛选并剔除重复构型,最终共计选出871 个结构用于构建深度学习势函数,随机选取其中88 个(占比10%)结构作为验证集,剩余783 个(占比90%)结构用于势函数的训练.

图2 β-Si3N4 的晶体结构 (a) 用于第一性原理分子动力学计算的体系(原子个数为140 个);(b) 用于深度学习分子动力学模拟的体系(原子个数为2200 个),其中绿色原子代表硅原子,红色原子代表氮原子Fig.2.Crystal structure of β-Si3N4: (a) The system for first-principles molecular dynamics calculations (140 atoms);(b) the system for deep potential molecular dynamics simulations (2200 atoms).The green atoms represent silicon atoms and the red atoms for nitrogen atoms.

2.2 深度学习势函数训练

本文采用DeepMD-kit[21]软件包训练深度学习势,该软件基于当下流行的深度学习框架Tensorflow[22]进行二次开发,能够实现多体势训练并保持计算精度几乎不损失.依据原子神经网络势的理论框架[12,23]可知,对于包含N个原子的体系,体系总能量可归结为每个原子的能量之和:

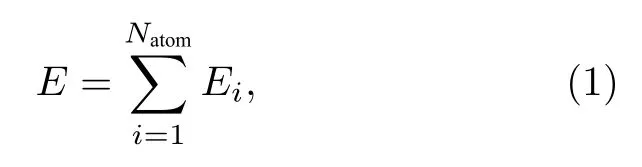
其中每个原子的能量Ei由该原子及其截断半径范围内的近邻原子位置所决定:

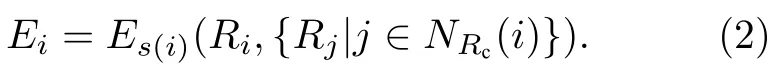
其中,Ri表示原子i的原子位置,Rj代表原子i的近邻原子j的原子位置,代表原子i的截断半径范围内近邻原子列表的索引集.

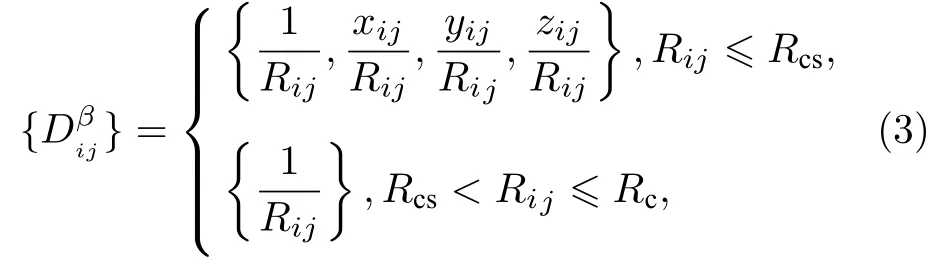
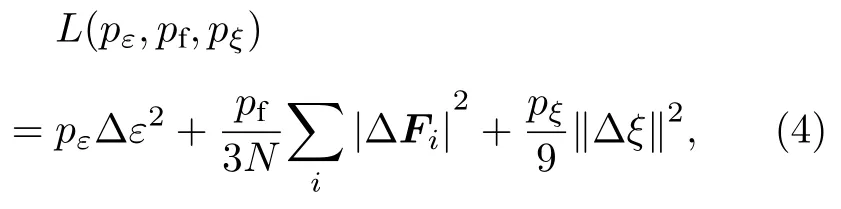
其中ps,pf和pξ分别代表能量项、受力项及维里项的可调前置因子;Δ 代表训练集数据与深度学习势预测值间的偏差;N代表原子数目;ε代表单个原子的能量;Fi代表第i个原子的受力信息;ξ代表维里张量.由于训练过程中没有包括维里值数据,将pξ设为0.对于损失函数中的能量和力误差,可调预因子的起始值分别为0.02 和1000,这意味着训练过程在初始阶段主要由力拟合控制.学习率从最初的1.0×10–3以指数形式下降到3.5×10–8,衰减率和衰减步长分别为0.95 和5000,训练步数设置为400 万步.

2.3 深度学习分子动力学模拟

借助DeepMD-kit 与LAMMPS[26](large-scale atomic/molecular massively parallel simulator)之间的软件接口,可以直接实现基于深度学习势的分子动力学模拟.本文使用深度学习势对含2200 个原子的β-Si3N4体系进行分子动力学模拟计算,具体实施过程如下: 体系中原子依据高斯分布进行速度初始化,时间步长设置为0.5 fs.首先,整个β-Si3N4体系在对应温度下进行热力学弛豫,弛豫时间为1 ns;其次,待体系达到热力学稳定状态后,开始每2000 步收集一次偶极矩数据用于后续计算,采集时长为1 ns.上述弛豫过程和数据采集过程均在NVT 系综完成,温度控制由Nosé-Hoover[27,28]热浴实现.为了比较经验势函数和深度学习势的差异,同样使用Tersoff[29,30]经验势进行了上述模拟.

3 结果与讨论

3.1 势函数训练及结果验证

为了验证训练结果的准确性,本文以均方根误差(root mean square error,RMSE)来衡量深度学习势的预测结果与AIMD 计算结果之间的差异.图3(a)为DLP 预测能量值与AIMD 计算值的对比,其中数据点沿对角线分布表明深度学习势的预测能力较好,能量的RMSE 为0.00550 meV/atom;图3(b)—(d)为x,y,z三个方向上DLP 原子受力预测值与AIMD 计算值对比,图中红色实线代表预测结果与计算结果相等,数据点离直线越近说明计算误差越小,RMSE 结果为7.800 meV/Å.由图3 可知,体系能量和原子力的数据点绝大多数都落在直线上,说明深度学习势的预测能力较好,预测结果已经达到了AIMD 计算精度.

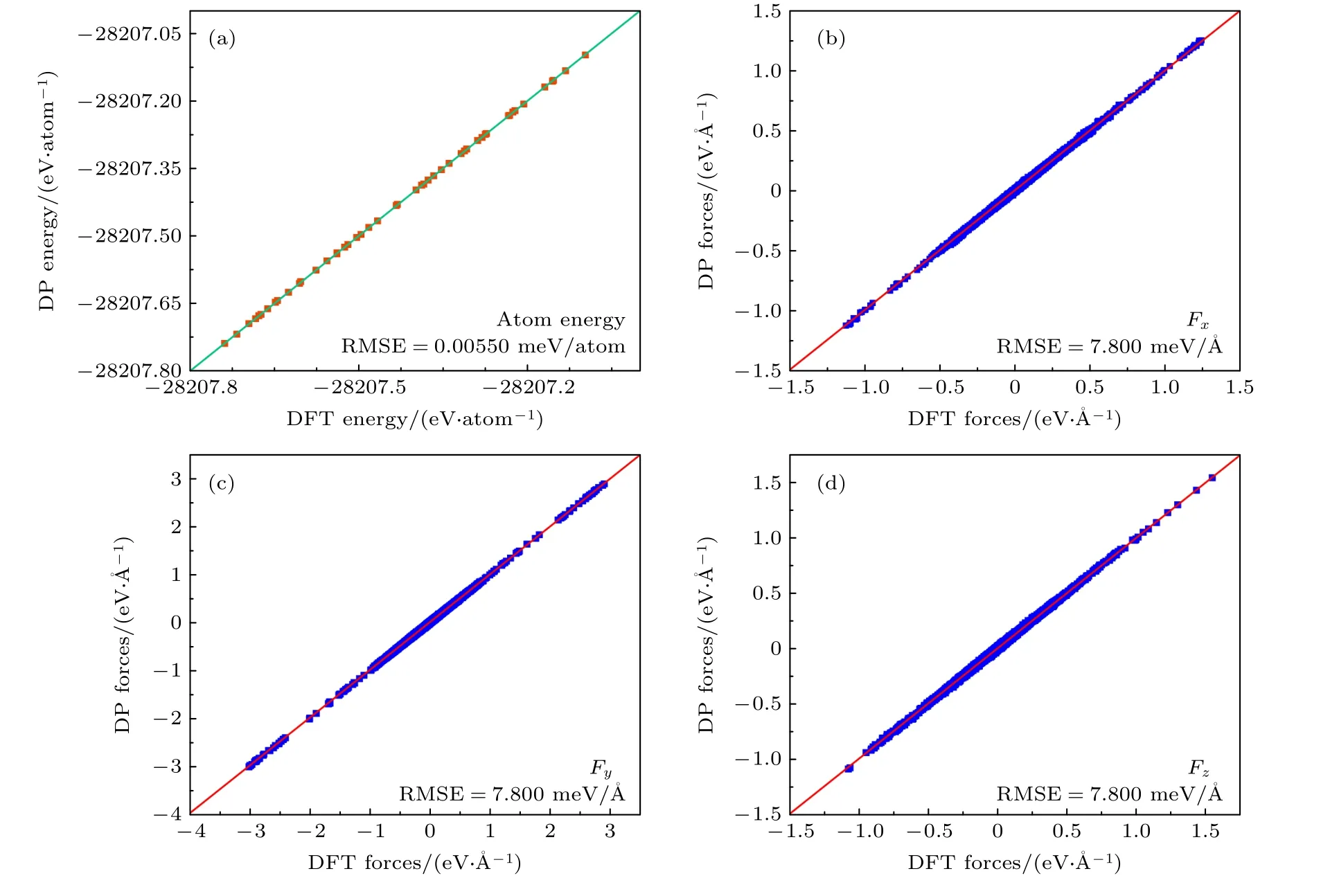
图3 (a) 第一性原理计算体系能量和深度学习势计算体系能量对比关系图;(b)—(d) 第一性原理计算原子受力和深度学习势计算原子受力对比关系图.其中图中直线代表y=xFig.3.(a) Comparison between the energy calculated by first-principles and that by the deep learning potential;(b)–(d) comparison between the forces on the atoms calculated by first-principles and those by the deep learning potential.The straight line in the figure represents y=x.

为进一步评估深度学习势相对于AIMD 计算的准确性,本文分别使用AIMD 方法和DPMD 方法计算了体系的径向分布函数进行对比,来验证深度学习势在描述结构演化过程中的精度和准确性.在相同温度条件下以AIMD 初始结构进行深度学习分子动力学模拟,计算体系原子数目均为140.两种模拟得到的Si-Si,Si-N,N-N 的径向分布函数如图4 所示,可以明显看到深度学习势准确地复现了AIMD 径向分布函数峰的形状和位置,表明深度学习势函数可以很好地描述体系的动力学性质.

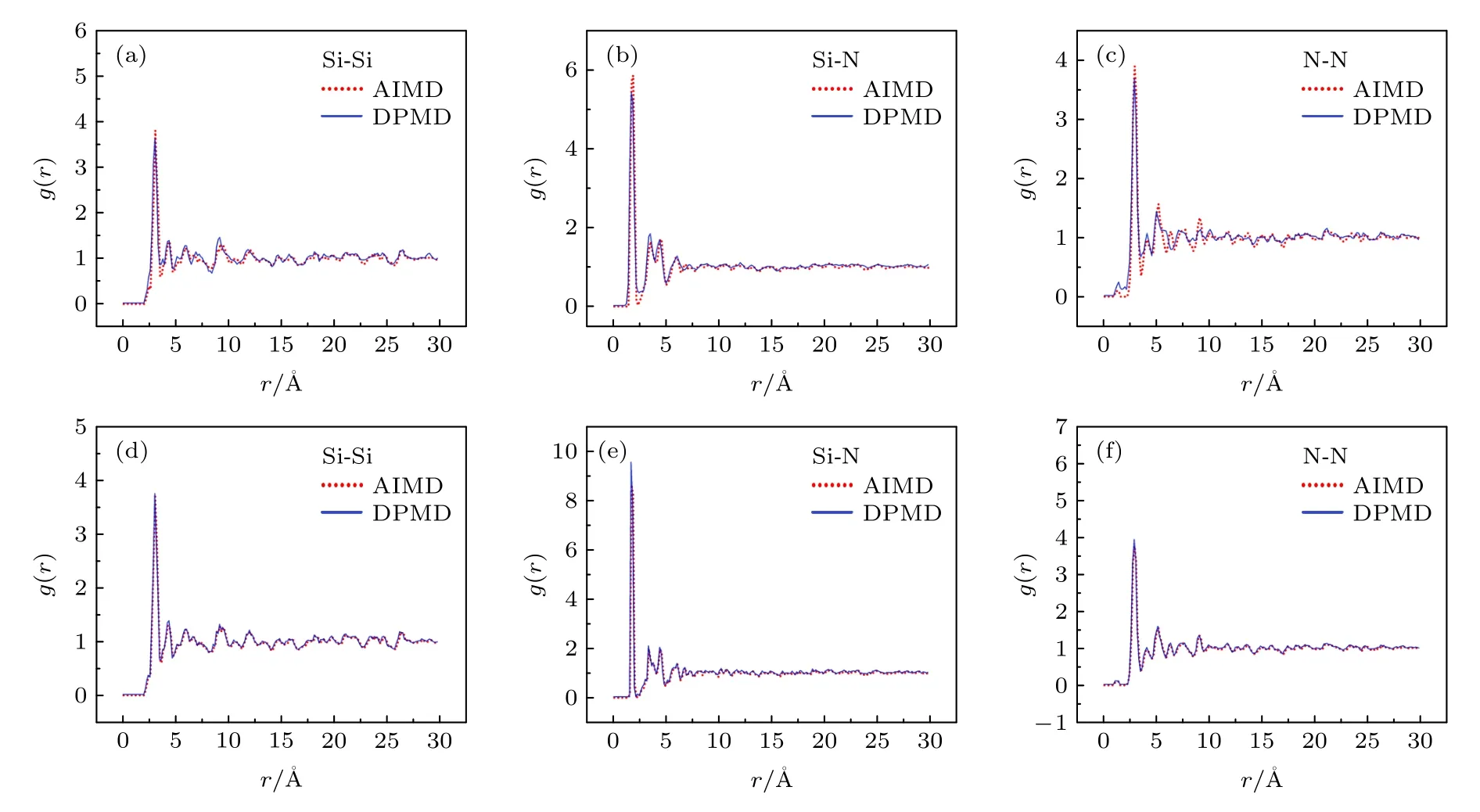
图4 (a)—(c) 300 K 温度下DPMD 与AIMD 计算径向分布函数对比图;(d)—(f) 1000 K 温度下DPMD 与AIMD 模拟径向分布函数对比图Fig.4.(a)−(c) Comparison of radial distribution function between DPMD and AIMD simulations at 300 K;(d)−(f) comparison of radial distribution function between DPMD and AIMD simulations at 1000 K.

3.2 弛豫时间及微波介电函数计算

本文依据德拜方程的修正式柯尔-柯尔[31](Cole-Cole)公式来计算β-Si3N4的微波段介电函数:

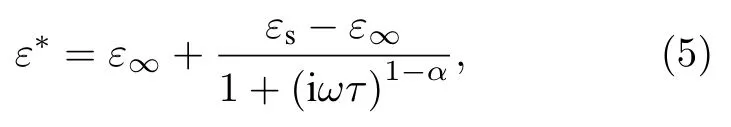
其中,ε∞为光频介电常数,εs为静态介电常数,ω为电磁波的角频率,τ为弛豫时间,α为弛豫修正因子.对应的介电函数实部和虚部分别表示为

式中,ε′为介电常数的实部,ε′′为介电常数的虚部.据(5)—(7)式可知,计算氮化硅材料频率相关介电函数需要确定弛豫时间、光频介电常数、静态介电常数以及弛豫修正因子等参数.由于高频与静态介电常数受温度影响较小,故采用0 K 温度下氮化硅的光频和静态介电常数用于计算,其值分别为4.27 和8.16[32].弛豫修正因子通常用于修正理论值与实验值间的差异,本文主要采用模拟计算的方法计算介电函数,因此将弛豫修正因子设置为0.弛豫时间能通过求解偶极矩自相关函数得到[17],偶极矩自相关函数计算如下:

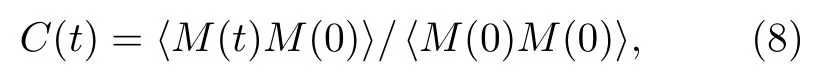
式中M(t)代表某时刻体系的总偶极矩,M(0)为初始时刻体系的总偶极矩.依据德拜模型,自相关函数通常以指数递减形式呈现,偶极矩自相关函数与弛豫时间存在如下关系:

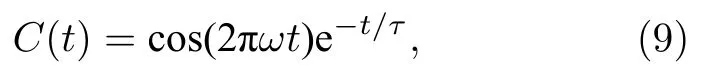
其中t为时间.

图5 为偶极矩自相关函数随时间变化曲线,将偶极矩自相关函数拟合成(9)式中的指数衰减形式,以确定弛豫时间τ.拟合过程如下: 首先通过分析得出偶极矩自相关函数存在局部最大值,即图5(a)中曲线的所有峰值.然后将得到的极值点以对数形式进行拟合,拟合结果如图5(b)所示,所得直线的斜率的倒数即为弛豫时间.偶极矩数据是按照一定频率进行采样的,部分数据并不能完全落在自相关函数的极值点处.因此,本文选择了数值大于其最近邻值的点作为极值的近似,这也会导致弛豫时间计算时中拟合数据与原始数据不能完全重合.通过上述方法计算了300—1000 K 温度范围内的弛豫时间,具体结果汇总在表1 中.结果发现,利用深度学习势与经验势得到的弛豫时间在数量级上相当,且随着温度的升高,弛豫时间均呈现下降的趋势,这是由于弛豫时间遵循阿伦尼乌斯(Arrhenius)定律,随温度升高呈下降的趋势[33].值得注意的是,Tersoff 势函数计算得到的弛豫时间绝大多数情况下大于DLP 的计算结果,但是结果的波动性较大.原因可能是Tersoff 势最多描述三体相互作用,其势函数形式只是粗略的拟合近似.深度神经网络在理论上可以用来逼近任何高维函数,具有表征多体势的优点,因此由DLP 计算得到的结果更加准确,所表现的物理图像更具说服力.

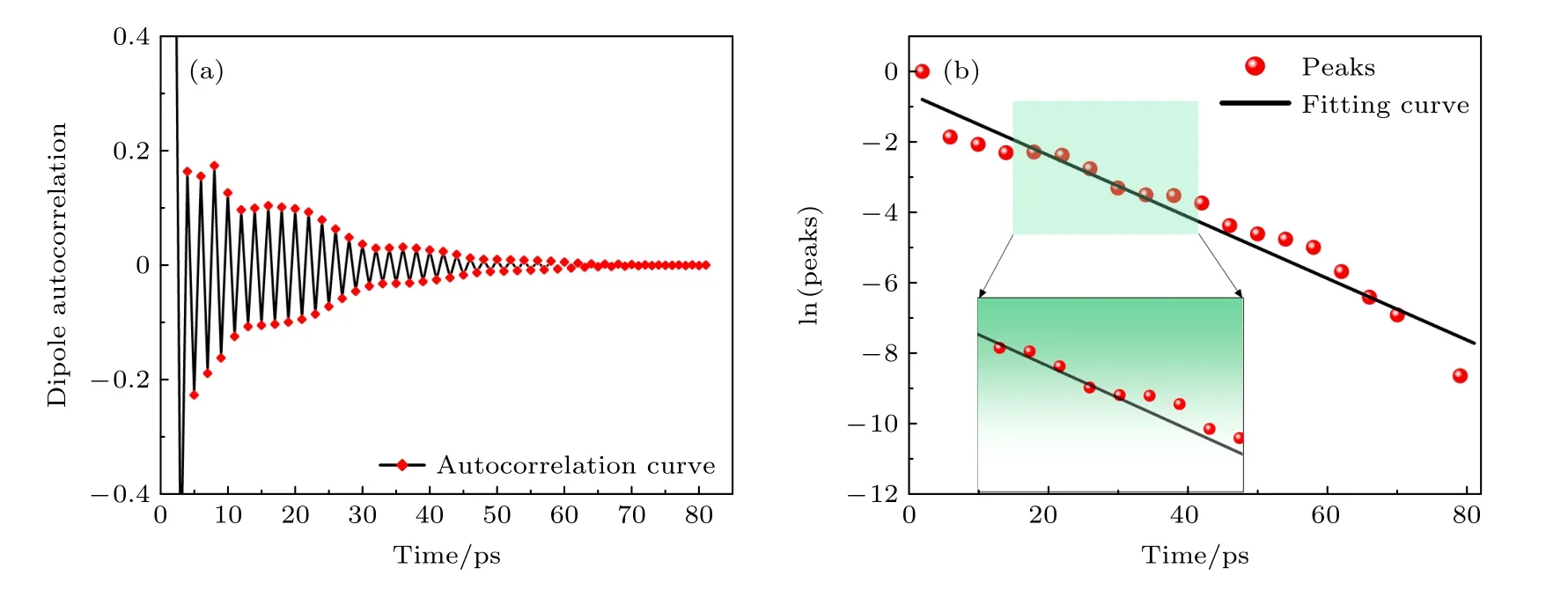
图5 运用深度学习分子动力学计算的700 K 温度下氮化硅偶极矩自相关函数 (a) 偶极矩自相关函数随时间的变化;(b) 偶极矩自相关极值点对数值随时间的变化Fig.5.Silicon nitride dipole moment autocorrelation function at 700 K calculated by the deep learning potential: (a) Dipole moment autocorrelation function versus time;(b) dipole moment autocorrelation polar point logarithm versus time.

根据(5)—(7)式和表1 中弛豫时间即可求得氮化硅的微波段 (0—100 GHz)介电函数.图6 展示了β-Si3N4在300—1000 K 温度范围内频率相关介电函数的实部和虚部.其中文献[34]结果为300—800 K 温度时在频率为8.2 GHz,10 GHz,12.4 GHz 时的介电函数实部.300 K 温度下,DLP和Tersoff 势在频率为8.2 GHz 时结果与实验值相差不大,但随着频率的升高,DLP 的结果与实验值更加接近.文献[35]为常温下氮化硅掺杂多壁碳纳米管后介电函数实部变化,随着频率的升高介电函数实部呈现下降的趋势,这与本文计算结果的变化趋势是相符的.因此,随着频率增大,介电函数实部呈现逐渐降低的趋势,DLP 的计算结果均大于Tersoff 势结果,但与实验值在数量级上更加吻合.从图6(b)给出的微波介电函数虚部来看,300 K温度下DLP 计算的介电函数虚部相比Tersoff 势更接近于实验值,表明了DLP 可以更好地描述β-Si3N4的高温微波介电特性.

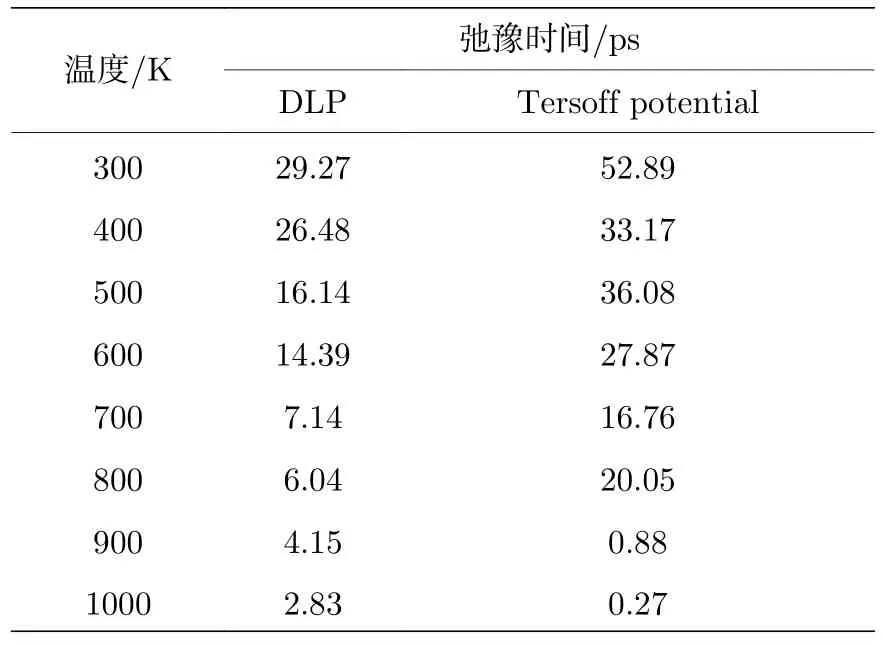
表1 不同温度条件下的弛豫时间Table 1.Relaxation time under different temperatures by DLP and Tersoff potential.

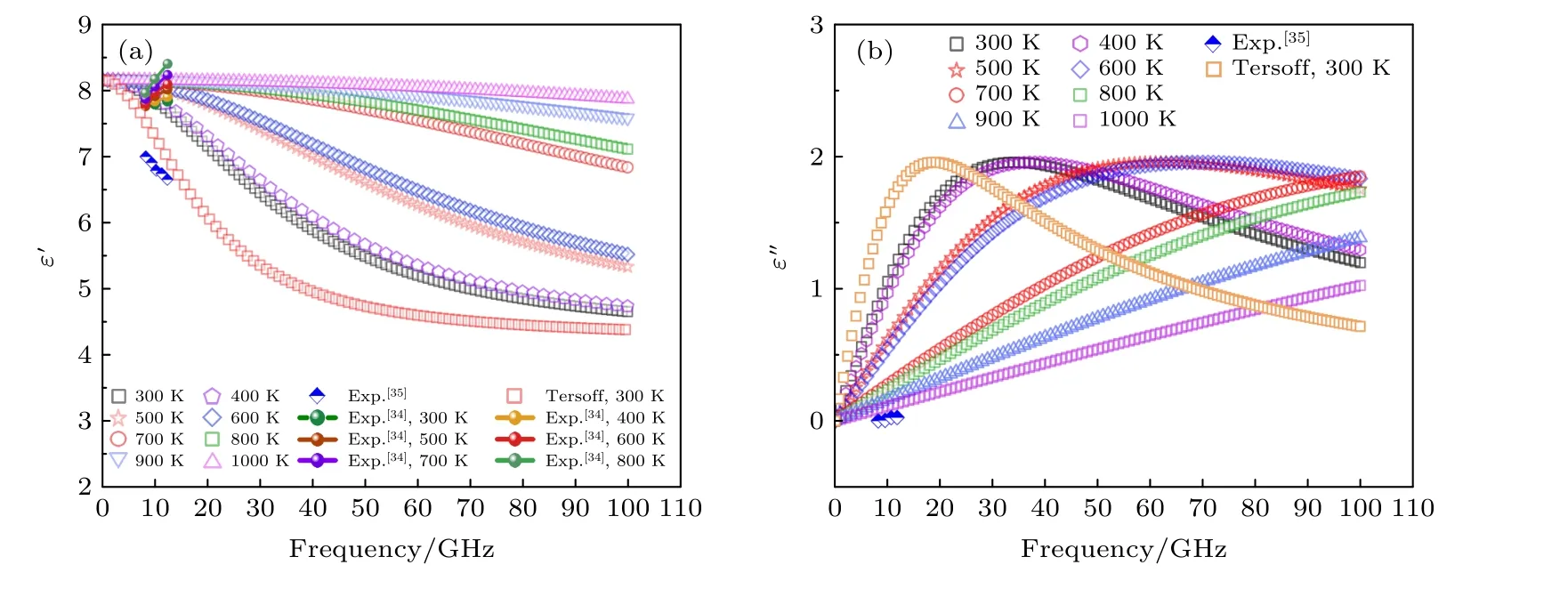
图6 (a) β-Si3N4 在不同温度时的频率相关介电函数实部;(b) β-Si3N4 在不同温度时的频率相关介电函数虚部.其中文献[34]仅给出了实部值,未给出虚部值.文献[35]给出了8—12 GHz 频率范围内的介电函数实验测量值Fig.6.(a) Real part and (b) imaginary part of frequency-dependent dielectric function of β-Si3N4 at varying temperatures.Note that only the real part is given in Ref.[34].The values of dielectric function in the frequency range of 8–12 GHz are given in Ref.[35].

对于Tersoff 势来说,其构造过程是先选择合适的数学表达式,然后通过实验数据拟合确定函数中的参数,因此经验势只能描述已知的性质.因此,利用Tersoff 势来计算高温氮化硅的介电特性还有待商榷.相比之下,基于第一性原理计算求解电子结构所得到结果是值得信赖的,而深度学习势是基于第一性原理数据进行训练拟合,因此深度学习势计算得到的氮化硅介电函数结果更加合理.

3.3 弛豫时间温度依变性模型

由德拜模型可知,弛豫时间是计算微波段介电函数的关键参数,掌握弛豫时间随温度变化规律是准确计算高温微波介电函数的重要前提.本文基于深度学习势弛豫时间计算结果,拟合得到了弛豫时间随温度变化曲线:

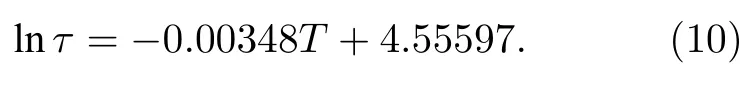
由图7 可知弛豫时间的对数随温度变化呈现线性下降的趋势且直线相关性较好,因此可判定此模型在对应温度范围内的有效性.结合(10)式和图7 可知,随着温度的升高,弛豫时间呈现指数下降的趋势.当温度高于1700 K,弛豫时间趋近于零.这是因为高温情况下极化损耗占比较少,需要考虑电子电导以及等离子的损耗贡献,这与文献[36]的报道结果一致.

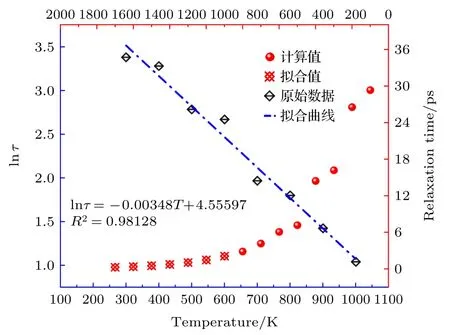
图7 弛豫时间随温度变化曲线,其中蓝色直线代表弛豫时间温度依变性模型,红色散点代表不同温度下弛豫时间变化曲线Fig.7.Relaxation time variation curves with temperature.The blue straight line corresponds to relaxation time temperature dependence model,and the red scattered points represent relaxation time variation curves at different temperatures.

3.4 计算效率测试

DPMD 方法实现了具有第一性原理高精度的大规模分子动力学模拟,在计算效率上也有了很大的提升.由于AIMD 方法很难实现数千原子体系的计算求解,故而此处选用原子数为140 的氮化硅体系分别测试了DPMD 模拟与AIMD 模拟的计算效率.本文采用了48 个Intel Xeon Platinum 9242 CPU 核心通过并行计算方式实现AIMD 模拟计算.DeepMD-kit 软件有CPU 和GPU 两种版本,本文选用后者并在Nvidia RTX 3080 进行了模拟计算,计算结果如图8 所示.可以看出,得益于GPU 加速,DPMD 模拟的计算速度大幅度提升,表明了DLP 在GPU 加速的条件下既能保持AIMD模拟的计算精度,又能在计算速度上有优异的表现.

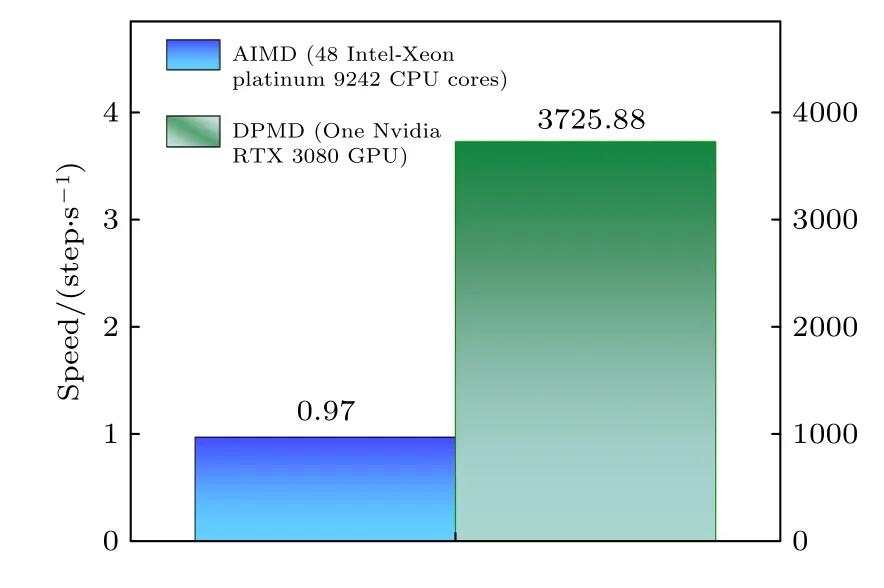
图8 DPMD (Nvidia RTX 3080 GPU 计算)与AIMD(48 个Intel Xeon Platinum 9242 CPU 计算)计算速度结果Fig.8.Computational speed of DPMD (running with a Nvidia RTX 3080 GPU) and AIMD calculations (running with 48 Intel Xeon Platinum 9242 CPU cores).

4 结论

本文基于DNN 对高温氮化硅分子晶体结构数据集进行训练得到深度学习势,并应用DPMD方法结合电介质理论研究了β-Si3N4的高温微波介电函数.相较于第一性原理计算结果,深度学习势所计算原子受力的RMSE 为7.800 meV/Å,体系能量的RMSE 为 0.00550 meV/atom,均能很好地预测正确的结果.由于深度学习势良好的训练结果,DPMD 在模拟氮化硅体系结构演化过程时的径向分布函数与AIMD 结果完全一致.同时发现,深度学习势计算得到的氮化硅高温微波介电函数与实验结果在数量级上保持一致.此外,基于深度学习势弛豫时间的计算结果,建立了弛豫时间随温度变化的数学模型,探明了弛豫时间的温度依变性规律.本文研究结果成功预测了氮化硅高温微波介电函数,为推动其在高温热透波领域的应用提供了基础数据支撑和科学依据.