飞秒激光加工熔融石英的理论和实验研究*
2022-12-31潘鹏晖吉鹏飞林根董希明赵晋晖
潘鹏晖 吉鹏飞 林根 董希明 赵晋晖
(北京理工大学机械与车辆学院,激光微纳制造研究所,北京 100081)
对单脉冲飞秒激光加工熔融石英进行了理论和实验研究,在追踪自由电子密度、温度和激光强度时空分布的基础上,量化了飞秒激光辐照熔融石英的电子动力学及瞬态材料光学和热物理的演变过程.通过将理论预测的烧蚀阈值、深度及轮廓,和实验结果进行比较,发现了理论预测结果与实验测量结果较好吻合,验证了本文所提出的理论模型的有效性.并进一步通过理论模型,揭示了在不同飞秒激光能量密度(也称“激光通量”)和脉冲持续时间(也称“脉冲宽度”)的辐照下,光致电离和碰撞电离中的自由电子弛豫时间演变规律,发现了自由电子弛豫时间对材料光学性质的演变和飞秒激光能量吸收过程起着至关重要的作用.理论模拟和实验测量均发现激光能量密度对烧蚀坑的形状有很大影响,即在激光能量密度略高于烧蚀阈值时烧蚀体积与激光能量密度呈线性关系.相较于皮秒激光而言,在飞秒激光辐照下烧蚀体积随着激光能量密度的增加而增大更为明显.因此,本文提出在略高于烧蚀阈值时可获得较高的加工效率,而在远高于烧蚀阈值时可获得良好的可重复性加工.
1 引言
飞秒激光脉冲与介电材料相互作用的机理研究,在基础研究[1−6]和工业应用[7−9]中都是十分活跃的研究领域.其中涉及一系列复杂过程,包括非线性电离产生自由电子、自由电子吸收激光能量以及材料去除[10−12].飞秒激光加工的最终结果取决于飞秒激光脉冲电子动态调控[13].在飞秒激光与介电材料的相互作用过程中,光致电离导致自由电子的初始产生,其电离速率取决于电场和激光强度[14].导带中的自由电子可以进一步通过碰撞,电离其他被束缚在价带中的电子.当自由电子密度接近临界密度,介电材料反射率急剧升高.激光脉冲能量在极短时间内被非常浅的区域吸收,导致表面材料烧蚀[15−18].多种不同类型的材料去除机制同时存在或发生瞬态演化,如库仑爆炸、静电去除、热熔化、相爆炸等[19].
目前许多科研工作者介绍了飞秒激光与介电材料相互作用的几种理论模型,特别是自由电子密度的时间演化速率.其中通量倍增模型是基于福克-普朗克方程的著名理论之一.许多飞秒激光加工介电材料的实验证明,该模型对自由电子密度的预测是较为准确的[16,17,20−22].光致电离通常由Keldysh 理论给出,该理论同时考虑隧穿电离和多光子电离作用的影响[20].而许多学者则采用了不同的模型来描述碰撞电离引发的自由电子激发和激光能量吸收[16−18],例如基于麦克斯韦分布和费米-狄拉克分布的模型[10,23].当自由电子的振荡频率等于入射飞秒激光的光学频率,透明介电材料的光学反射率和吸收系数就会发生显著变化.根据自由电子气体的经典描述[24],普遍采用Drude 模型来计算光学性质.值得注意的是,Drude 碰撞频率不是一个微观参数,而是在激光激发的宽禁带材料中高度瞬态变化的现象参数[25].通常由表征导带中电子能量损失和光子能量吸收的瞬态散射率来描述[26].电子的散射包括在低电子激发态时占主导的电子-声子散射和在高电子激发态时占主导的电子-离子散射.
现有的模型仅通过对比烧蚀阈值进行验证,而没有给出更为全面的烧蚀结果.例如Chimier 等[10]仅对比了脉宽在7—300 fs 范围内的模拟烧蚀阈值与实验结果.Christensen 和Balling[27]预测得到的烧蚀深度与实际加工结果差异显著.本文以熔融石英为例,在改进量子等离子体模型[28]的基础上,通过实验与数值研究激光参数对飞秒激光加工介电材料的影响.同时通过阈值能量密度、烧蚀深度和烧蚀轮廓三个方面的实验结果与数值模拟对改进的模型进行验证[10,22,29,30].此外,本文还讨论了飞秒激光加工过程中光学特性的瞬态变化规律,并预测了材料内部电子温度、自由电子密度和激光强度的时空分布.分析发现,自由电子弛豫时间的演化对光学性质和飞秒激光能量吸收起到十分重要的作用.最终,本文探究并揭示了激光能量密度和脉冲持续时间对飞秒激光加工结果的影响规律.
2 建模与仿真
2.1 电子激发
飞秒激光入射熔融石英最先引发电子激发过程,其包括光致电离与碰撞电离.由于飞秒激光脉冲将价带中的电子电离到导带,这决定了飞秒激光烧蚀的一系列后续过程.因此,探明自由电子密度ne的演化十分重要.考虑到电子复合过程,使用以下方程式来模拟自由电子密度ne的时间演化[1,15,16]:
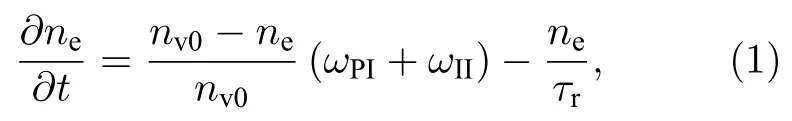
式中,t对应时间,ωPI是光致电离速率,ωII是碰撞电离速率,τr是衰减时间常数[31],nv0是熔融石英中的电子密度总数[32].饱和项 (nv0−ne)/nv0通过考虑价带中可电离的电子密度的最大值来描述ne的时间演化.值得注意的是,对于单脉冲激光辐照熔融石英而言,在高于烧蚀阈值的激光能量密度下,自陷激子对熔融石英中的载流子弛豫没有明显贡献,因而自陷激子的影响被忽略[33].光致电离速率可以用Keldysh 理论来确定[14]:

式中,ϕ(a)是道森积分,〈x〉是x的整数部分.
碰撞电离速率与激光强度呈线性关系,由(4)式计算求解[20]:

式中,ai是碰撞电离常数[29].
2.2 自由电子弛豫时间
在激光辐照过程中,自由电子的弛豫时间主要由电子散射决定.当自由电子温度Te低于费米温度TF时,电子-声子碰撞产生的电子散射的贡献占据主导.而当Te远高于TF时,电子散射率归因于电子-离子碰撞.根据马西森定则同时考虑电子-声子碰撞和电子-离子碰撞,自由电子弛豫时间τe可以表示为
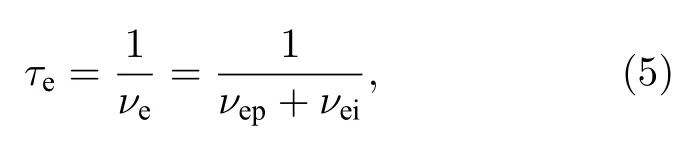
式中,νe是电子散射速率,νei和νep分别是电子-离子和电子-声子的散射速率.分别由以下公式求解:
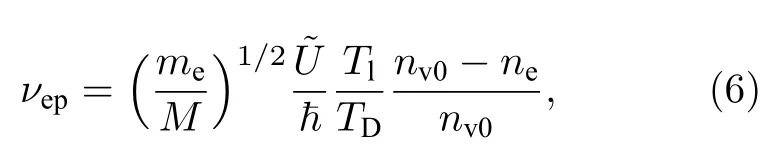
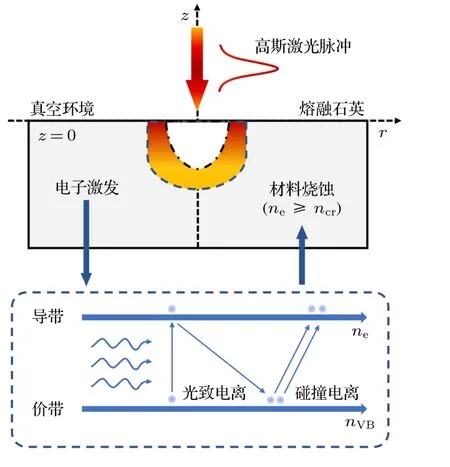
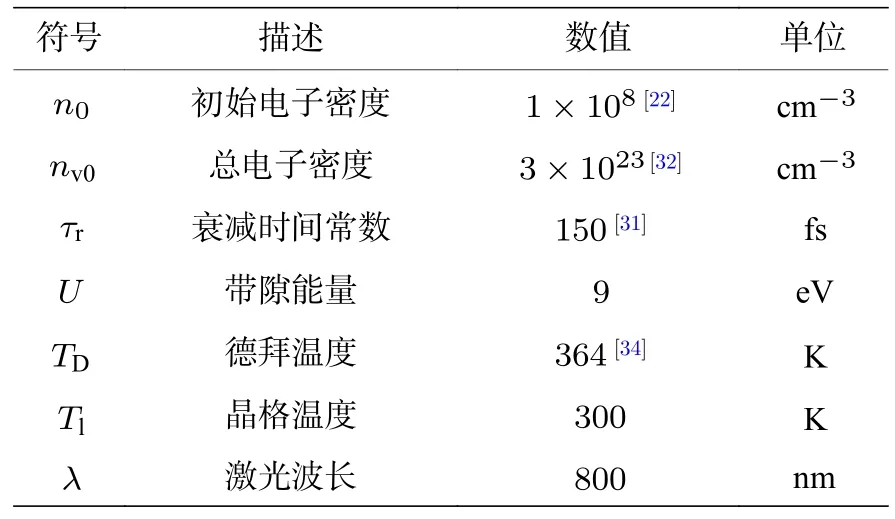
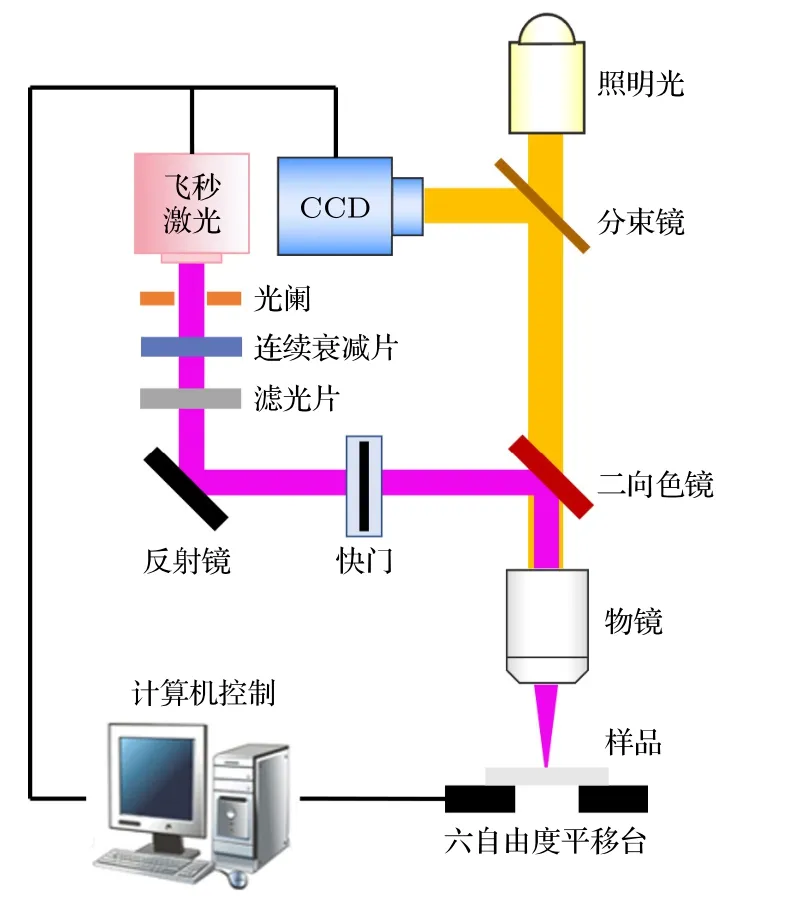
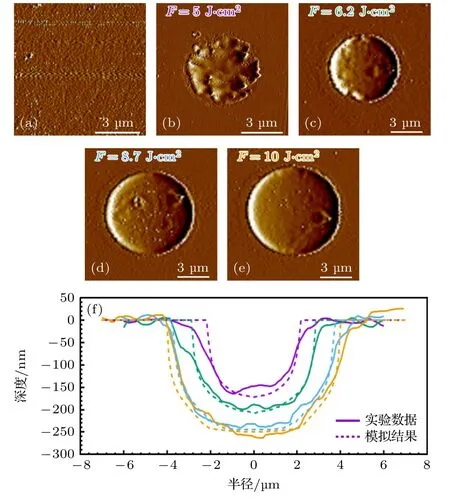
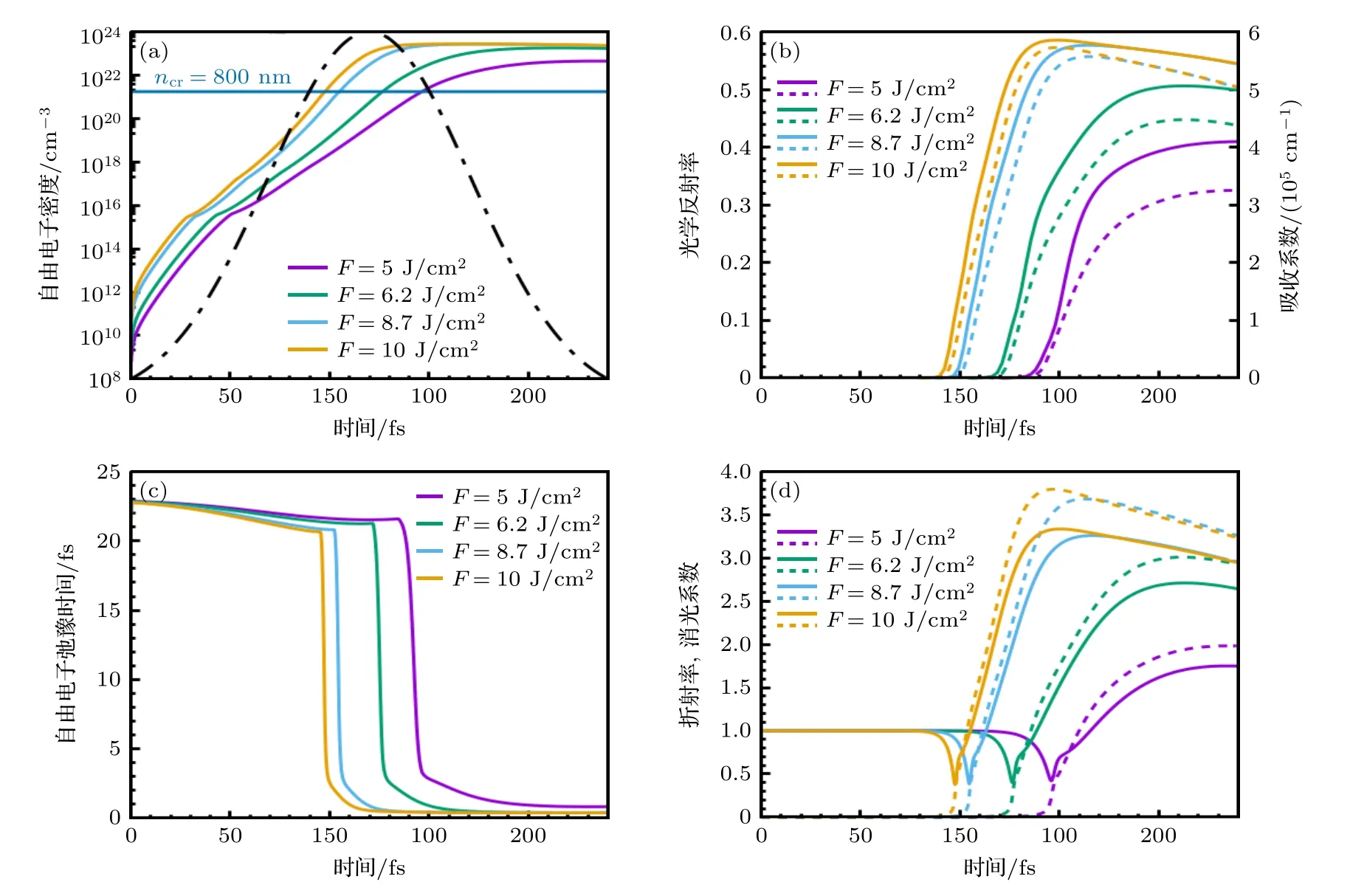
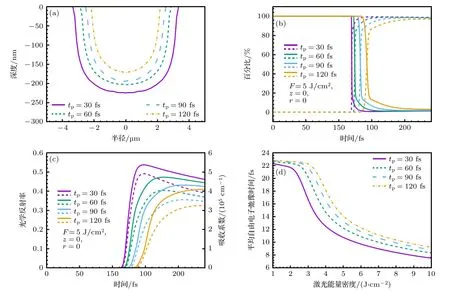
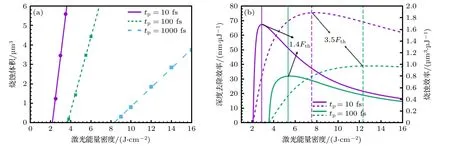
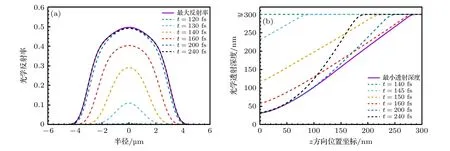
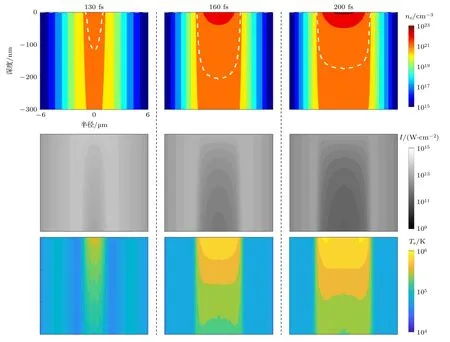
式中,me是电子质量,M是原子质量单位,TD是德拜温度[34],Tl为室温下的晶格温度.值得注意的是,对于低电子温度而言(Te νei则由Spitzer 公式给出[37,39,40]: 式中,Z是平均离子电荷(对于熔融石英而言,Z=5[32]),EeV是单位为 eV 的平均电子动能.库仑对数lnΛ的计算公式为[41] 式中,bmax=(kBTe/me)1/2/max(ω,ωp) 是最大碰撞参 数,bmin=max[Ze2/kBTe,ℏ(mekBTe)1/2] 是最小碰撞参数. 被飞秒激光辐照后的熔融石英所生成等离子体的瞬态光学特性,可以通过以下公式给出的介电函数来确定: 复折射率f由以下公式计算求解: 折射率f1和消光系数f2由介电函数的实部和虚部导出.因此,f1和f2由以下公式给出: 光学反射率由菲涅耳公式求得 同时,光学吸收系数可通过以下公式求解: 式中,Lop是光学透射深度. 电子由价带被激发到导带后,进一步吸收激光能量使得电子动能增加.该模型假设电子在导带中服从费米-狄拉克分布其中ε,µ,kB和Te分别表示能量状态、化学势、玻尔兹曼常数和电子温度.通过这种假设,简化了模型的计算,而不是一系列离散能级[27,42].飞秒激光加热自由电子过程中,自由电子温度随时间的变化可由以下公式描述[43]: 平均电子动能〈ε〉可通过以下公式求解: 式中,nk和εk分别表示k能级对应的自由电子数和电子动能,Ne为总自由电子数. ρ(ε)对应的是自由电子态密度[45]: 如图1 所示,在本研究中采用高斯激光束照射熔融石英,设定飞秒激光脉冲的传播方向与z方向相反.z <0 处的区域表示的是熔融石英.激光强度表示为 图1 数值模型中几何和现象的示意图Fig.1.Schematic illustration of the geometry and phenomenon in the numerical model. 式中F是入射激光能量密度,tp是脉冲持续时间,R是光学反射率,α是吸收系数,r是从给定点到激光束中心的距离,r0是定义为激光强度衰减为激光束中心最大强度的 1/e2的半径,z是从给定点到上表面的距离.吸收系数α包括两个部分: 一部分αPI用于自由电子电离.αPI可以通过公式αPI=求解.另一部分αh是用于电子加热的激光能量吸收,数值上等于光学吸收系数αop. 本研究中假设当瞬态ne达到临界密度ncr时材料发生烧蚀.将ne≥ncr作为烧蚀标准的方法被广泛用于预测介电材料烧蚀判据[15−18,20].当ne≥ncr时,光学反射率大大增加,导致熔融石英从透明变为不透明.同时,飞秒激光能量沉积到熔融石英中的光学穿透深度大大降低.因此,能量被沉积到一个较浅的区域,材料去除机制占主导地位,通过电离自由电子以高浓度迁移到材料表面,诱发库仑爆炸,并通过电子子系统到晶格子系统的电子-声子耦合能量传输诱发爆炸沸腾.最终,材料发生烧蚀,出现烧蚀坑.这里ncr表示临界自由电子密度,对应于自由电子的振荡频率等于入射飞秒激光的光学频率时的ne值,由以下公式求解: 式中,λ是飞秒激光波长,c是光速,me是电子质量,ϵ0是自由空间的介电常数. 在数值计算中,为了更好地展示飞秒激光与熔融石英相互作用的整个过程,所计算的时间区间的中间点对应为激光强度峰值处,时间步长取 0.1 fs .ne,Te,R,Lop和ce的时空演变通过如下迭代计算: 1) 自由电子密度ne的分布通过使用当前时间步长的激光强度I求解; 2) 电子温度Te的分布是使用I,α,ne和ce在当前的时间步内获得的; 3) 通过使用步骤1)中最后一个自由电子密度和步骤2)中的电子温度来更新〈ε〉,ce和τe; 4) 更新介电函数、光学特性和激光强度分布. 如果初始自由电子温度和自由电子密度收敛到0.01%的标准,模拟将进入下一时间步,并从步骤1)—4)开始,直到整个模拟周期结束. 通过确保迭代在初始状态下的收敛性,材料性质是自洽的,这确保了后续计算的准确性.在每个步骤中,通过检查自由电子密度是否符合标准ne≥ncr来判断材料烧蚀(如图1 所示,其中nVB表示价带电子密度,即未发生电离的电子密度).表1列出了模拟中激光脉冲和材料的参数. 表1 模型中用到的常数Table 1.Constants used in the model. 图2 描述了飞秒激光烧蚀熔融石英的实验装置的原理图.使用Spectra Physics 公司的Spitfire超快放大器(800 nm),其重复率高达 1kHz,脉冲能量高达 3mJ .根据实验条件,使用光阑和几个滤光片来降低激光功率.输出激光的功率可以通过一个连续可调的衰减片进一步调整.通过机电快门精确控制照射时间和脉冲的数量.激光脉冲被导入一个5 倍的物镜,并垂直聚焦在安装在6 轴运动平台上的样品上,导致半径为r0≈6µm 的光斑在1/e2的强度分布上接近高斯分布.采用激光系统的单发模式确保每个作用位置只有一个激光脉冲照射到样品上.熔融石英样品的尺寸是10 mm × 10 mm,1 mm 厚,单面抛光清洁.在物镜前测量激光脉冲宽度为 120 fs .通过共聚焦激光扫描显微镜(confocal laser scanning microscope,CLSM)精确测量不同能量脉冲(每点一脉冲)所形成的烧蚀区域、烧蚀深度和烧蚀形状.通过Liu plot 方法[12,46]得到熔融石英的烧蚀阈值约为Fth=4.1 J/cm2.将样品浸泡在95%纯度的乙醇中,通过超声波浴清洗以去除所加工后样品表面的残留物.通过原子力显微镜(atomic force microscope,AFM)进一步观察表面形貌. 图2 飞秒激光烧蚀熔融石英实验装置示意图Fig.2.Schematic diagram of the experimental setup in femtosecond laser ablation of fused silica. 采用波长为 800 nm 的飞秒激光脉冲对数值模型进行了验证.通过比较飞秒激光加工熔融石英的计算结果和实验测量结果,验证了该模型[10,22,29,30].阈值能量密度和脉冲持续时间之间的关系如图3(a)所示.从图3(a)可以观察到,在脉冲持续时间从10—1000 fs 的范围内,模拟结果与多数实验的结果较为吻合.烧蚀阈值随着脉冲持续时间的增加而增大.这是由于当激光脉冲能量固定,在较短的脉冲持续时间下相应的激光强度将更高,使得多光子电离和隧穿电离过程更为显著,对应的光致电离速率较大.同时,由于碰撞电离速率与激光强度呈线性关系[20],较高的激光强度能够得到较大的碰撞电离速率,加快自由电子密度达到临界密度,进而发生烧蚀.图3(b)展示的是脉冲持续时间为 120和300 fs下,不同激光能量密度下的烧蚀深度与实验数据对比[30].对于本研究中的熔融石英而言,预测的烧蚀深度与实验结果非常吻合.此外,数值和实验结果均表明,随着激光能量密度的增加,烧蚀深度逐渐接近饱和.这是由飞秒激光照射下光学特性的显著变化引起的.随着激光能量密度的增加,熔融石英吸收的能量在光学特性的影响下趋于饱和,最终导致烧蚀效率降低[30]. 图3 (a) 给定脉冲持续时间的烧蚀阈值与实验结果对比,其中深蓝色三角形、绿色误差条、蓝色空心矩形和橙色空心三角形分别来自本研究的实验结果以及文献[29,22,10];(b) 在脉冲持续时间为 120和 300 fs 时,烧蚀深度作为激光能量密度的函数,其中深蓝色三角形、红色空心圆形分别来自本研究的实验结果、文献[30]Fig.3.(a) Threshold fluence at the given pulse duration in comparison with experimental results.The navy-blue triangle,green error bar,blue unfilled square,and orange unfilled triangle come from the present study,Refs.[29,22,10],respectively;(b) the ablation depth as a function of laser fluence for the cases with pulse duration of 120and 300 fs .The navy-blue triangle and red unfilled circular come from the present study and Ref.[30],respectively. 图4(a)给出了熔融石英样品未加工前的表面形貌.可以发现抛光清洁后的样品表面没有污染物的存在,确保了加工结果的准确性.图4(b)—(f)展示的是脉冲持续时间为 120 fs,激光能量密度分别为 5—10 J/cm2的原子力显微镜快照,以及共聚焦显微镜1D 剖面与模型预测的结果对比.结果表明激光能量密度强烈影响烧蚀坑的轮廓.实验测量(实线)与理论模拟(虚线)的对比结果较好.相较于激光能量密度为 5J/cm2的类高斯型烧蚀形貌,激光能量密度为 8.7 和 10 J/cm2的烧蚀坑底部的分布要平坦得多.同时,材料烧蚀趋近于饱和,形成大小较为一致的烧蚀轮廓.在飞秒激光加工介电材料[47]和半导体材料[48]中也观察到类似的烧蚀坑底部的平坦区域.对于高激光能量密度的情况,激光强度的空间分布和产生的等离子体光学特性的显著变化导致平底轮廓.而对于低激光能量密度加工而言,烧蚀轮廓在一定程度上具有高斯分布的特征[30],即形成类高斯型的烧蚀坑.综上所述,烧蚀阈值、烧蚀深度和烧蚀轮廓的对比结果证明了本研究提出的数值模型的有效性. 图4 (a) 熔融石英样品未加工前表面形貌,(b)—(e) 原子力显微镜快照,以及(f)共聚焦显微镜1D 剖面与模型预测的结果对比Fig.4.(a) Surface morphology of fused silica before processing,(b)–(e) AFM snapshot and (f) CLSM 1D profile in comparison with simulation results. 图5 为对于波长为 800 nm 的飞秒激光加工熔融石英时,不同能量密度下激光束中心自由电子密度和光学特性的时间演变.在图5(a)中还绘制了激光波长为 800 nm 情况下的临界密度和入射激光脉冲的时间分布图以供参考.对于波长为800 nm的情况,自由电子密度在模拟开始时迅速增加.电离从光致电离开始,当电子动能在光致电离贡献下达到较高水平时,碰撞电离开始主导自由电子的产生.可以发现随着激光能量密度增大,自由电子密度上升速率增大.在激光能量密度为5,6.2,8.7和 10 J/cm2的情况下,自由电子密度分别在146.5,126.7,104.9和 97.7 fs达到临界密度(ncr,800nm=1.74×1021cm−3).从图5(b)可以发现,包括光学反射率和吸收系数的光学特性在自由电子密度接近临界密度时开始急剧上升.此时熔融石英处于高激发态,材料表面形成等离子体并具有类金属特性,同时材料开始由透明物质向非透明物质转变.对比能量密度为 8.7 和 10 J/cm2的模拟结果可以发现,这两种激光能量密度作用下产生的瞬态光学反射率和吸收系数分别在激光强度峰值附近几乎一致.对应的自由电子密度约为 1023cm−3.后续随着自由电子复合,反射率和吸收系数都出现了一定程度的下降.结果表明,随着辐照在熔融石英的激光能量增大,沉积在材料内部的能量趋近于饱和,同时大部分的能量都被材料反射.这也解释了图3(b)中烧蚀深度在高能量密度下趋近饱和的情况.图5(c)展示的是不同激光能量密度下自由电子弛豫时间随时间的演化过程.在初始阶段,自由电子弛豫时间下降并不明显.随着电子激发加剧以及自由电子温度上升,自由电子有效碰撞频率随之增大,对应于自由电子弛豫时间急剧下降,最终达到约 10−1fs .在其他研究工作中也同样得出对于电子动能 0—6 eV 的情况下,自由电子弛豫时间大约在 101—10−1fs 范围内是较为合理的[49,50].图5(d)给出模拟得到熔融石英表面折射率(实线)和消光系数(虚线)随时间的演化过程,分别对应(10)式中复折射率的实部与虚部,其中消光系数表征介质对光的吸收.当自由电子密度接近临界密度时,折射率下降至极小值.随着激光能量吸收,表面折射率和消光系数发生急剧上升,而后逐渐缓慢下降.可以发现在不同的能量密度下,自由电子弛豫时间和光学特性急剧变化的时刻均与自由电子密度达到临界密度的时刻较为一致,因此自由电子密度的演化对分析激光与材料相互作用具有十分重要的意义. 图5 脉冲持续时间 tp=120 fs,激光能量密度 F=5,6.2,8.7 和 10 J/cm2 时,(a) 自由电子密度、(b) 光学特性(光学反射率(实线)和吸收系数(虚线))、(c) 自由电子弛豫时间、(d) 折射率(实线)和消光系数(虚线)在 r=0,z=0 处的时间演化Fig.5.Temporal evolution of (a) free electron density,(b) optical properties (optical reflectivity (solid lines) and absorption coefficient (dash lines)),(c) free electron relaxation time,and (d) refractive index (solid lines) and extinction coefficient (dash lines) at r=0,z=0,with tp=120 fsand F=5 ,6.2,8.7and 10 J/cm2 . 对于飞秒激光与熔融石英的相互作用,脉冲持续时间的影响尤为重要.图6(a)显示了激光能量密度为 5J/cm2,在不同脉冲持续时间tp下形成的烧蚀坑轮廓.当tp减少时,烧蚀坑在半径和深度方向上都会延伸.相较于图4 展示的激光能量密度对烧蚀轮廓的影响,在所考虑的激光脉冲持续时间范围内,烧蚀坑形状与激光脉冲持续时间之间没有明显的关系.而烧蚀坑的大小受峰值强度的影响.在相同激光能量密度下,较短的脉冲持续时间能够产生更高的峰值激光强度,这促进材料内部电子激发使得自由电子密度更快达到临界密度,而后熔融石英转变为不透明的等离子体并吸收激光能量,通过库仑爆炸等机制引发材料的烧蚀.在熔融石英被飞秒激光激发产生等离子体的过程中,有效电子碰撞速率νe由较低激发状态下的电子-声子碰撞主导向较高激发状态下的电子-离子碰撞主导转变.如图6(b)展示的是不同脉冲持续时间下,电子-声子碰撞速率νep(实线)和电子-离子碰撞速率νei(虚线)的效应百分比随时间演变过程.初始阶段均由电子-声子碰撞主导有效电子碰撞,而后快速地向电子-离子碰撞过渡.随着电子激发的增加,晶格的恢复力逐渐减弱.因此,散射声子的能量逐渐减少,最终电子-声子散射逐渐消失.从图6(b)可以发现从νep为主过渡到νei为主的时间取决于脉冲持续时间tp.结果表明,激光脉冲持续时间决定了电子激发的速率.如图6(c)所示,不同的激光脉冲持续时间会引起不同的光学特性响应.可发现吸收系数(光学透射深度的倒数)随脉宽的增加而单调下降.这是由于较短的脉宽能够得到较大的峰值激光强度,促使非线性电离产生的自由电子密度更快达到临界密度,而后熔融石英转变为不透明的等离子体,而将入射飞秒激光的能量吸收局限在熔融石英表层很浅的区域,继而引发材料的烧蚀.图6(d)显示了不同激光脉冲持续时间下的平均自由电子弛豫时间与激光能量密度的关系.平均弛豫时间显示出随着激光能量的增加而整体下降的趋势.当激光能量密度接近烧蚀阈值时,平均弛豫时间的下降更为明显.这表明,随着激光能量密度的增加,在较短的脉冲持续时间内,熔融石英更容易被激发以促进等离子体的产生.同时,自由电子密度上升,电子-离子碰撞加剧,这使得自由电子弛豫时间明显下降. 图6 不同激光脉冲持续时间(F=5 J/cm2)下模拟得到的(a) 烧蚀坑形状、(b) 电子-声子碰撞(实线)和电子-离子碰撞(虚线)的效果百分比的时间演变、(c) 反射率(实线)和吸收系数(虚线)的时间演变,以及(d) 不同能量密度下的平均自由电子弛豫时间Fig.6.(a) Ablation crater shape,(b) temporal evolution of effective occupation of electron-phonon collision (solid line) and electronion collision (dashed line),(c) temporal evolution of optical reflectivity (solid line) and absorption coefficient (dashed line) for different laser pulse durations (F=5 J/cm2).(d) Average free electron relaxation time at different fluences. 图7(a)显示了不同激光脉冲持续时间tp下烧蚀体积与激光能量密度的关系.同时还绘制了烧蚀体积的线性拟合图.模拟成功预测出实验观察到的熔融石英烧蚀体积与激光能量密度之间的线性关系[51].当激光脉冲宽度为 10 fs 时,烧蚀体积对激光能量密度的变化非常敏感.对于脉冲持续时间较短的激光,当能量密度略高于烧蚀阈值时,很难精确控制熔融石英的微小体积烧蚀,如图4(a)所示.这也解释了由于激光能量密度略高于阈值能量密度,飞秒激光烧蚀的可重复性非常困难[52].此外,30 fs激光对应的斜率分别是 100和 1000 fs激光的 2.2 倍和 8.5 倍,这表明对于较长的激光脉冲持续时间,对激光能量密度的敏感性并不明显.如图7(b)所示,随着输入激光能量密度进一步增大,将出现烧蚀坑深度去除效率(实线)和烧蚀效率(虚线)饱和,然后逐渐下降.烧蚀坑深去除效率在接近阈值的能量密度(约 1.4Fth)下达到峰值,这是由于短脉冲促进的强吸收导致的.而此时自由电子密度仍然低于极限值(nv0),因此随着激光能量密度进一步增大,会继续吸收激光能量用于材料的去除.在激光能量密度大约 3.5Fth达到峰值烧蚀效率.而后材料去除出现饱和,对应于烧蚀效率开始下降.因此,在激光能量密度 1.4Fth—3.5Fth的范围内能够实现较高的飞秒激光加工效率和能量利用率.但由于在烧蚀特征(烧蚀坑深度、烧蚀体积)对短脉冲激光的敏感性较高,精确度稍低.对于高于 3.5Fth的饱和区间而言,由于在应用的能量密度下往往出现较为一致的平底型烧蚀轮廓,在极宽的能量密度范围内具有良好的可重复性,能够实现对超短脉冲的精确加工.在这种情况下能够降低对激光能量的稳定性的要求.然而在较高能量密度下加工区域会出现热影响区增大等问题,与接近烧蚀阈值的激光工艺相比,加工质量会有所下降.这是由于高能量沉积引发的更强烈的热机械效应.因此,在飞秒激光纳米/微米加工中,如为实现飞秒激光加工效率和能量利用率的迅速提升,可选择 1.4—3.5 倍烧蚀阈值范围内的能量密度;如为获得良好的可重复性加工结果,可使用高于 3.5 倍烧蚀阈值的能量密度进行加工. 图7 (a) 不同脉冲持续时间下烧蚀体积与激光能量密度的关系.计算结果用点表示并进行线性拟合;(b) 不同脉冲持续时间下深度去除效率和烧蚀效率与激光能量密度的关系Fig.7.(a) Ablation volume as a function of laser fluence for different pulse durations.The calculated results are expressed by points and linear fitted in terms of the solid lines.(b) The depth removal efficiency and ablation efficiency as a function of laser fluence for different pulse durations. 图8 显示了激光能量密度为 6.2 J/cm2、脉冲持续时间为 120 fs 的飞秒激光辐照时,光学特性的时空演变,包括材料表面的光学反射率和z方向位置的光学透射深度.其中实线给出了最大反射率及最小透射深度,虚线则代表不同时刻下的光学反射率和透射深度大小.如图8(a)所示,在自由电子密度未激发达到临界密度之前(t=120 fs),半径为6 µm的高斯光束区域的光学反射率几乎为 0 .当激光束(r=0)中心的ne达到ncr之后,光学反射率开始急剧增加,增加的趋势在径向扩展.r=0 处的光学反射率从几乎为 0增加到 0.52 .这表明入射激光主要被反射,熔融石英变得不透明,其区域半径达到约4 µm.在图8(b)中,初始阶段的光学透射深度Lop远大于设定的材料厚度.当时间达到 140 fs 之后,材料表面的Lop逐渐下降至 30.7 nm .由于复合过程,熔融石英内部的Lop开始缓慢增大直到模拟结束.在激光照射过程中,熔融石英的光学性质发生了显著变化,并通过实验进行了观察和验证[53].结果与之前的假设一致,即随着熔融石英瞬态光学性质的快速变化,一些激光能量被反射.只有一部分激光能量被吸收并沉积在非常浅的区域,最终导致材料烧蚀. 图8 脉冲持续时间 tp=120 fs、激光能量密度 F=6.2 J/cm2时,(a) 材料表面上的光学反射率和(b)光束中心处 z 方向上的光学透射深度的时空演化Fig.8.Spatiotemporal evolution of (a) optical reflectivity on the material surface (z=0) and (b) penetration depth in the z-axis direction (r=0) with tp=120 fsand F=6.2 J/cm2 . 为了进一步探索飞秒激光和内部材料之间的相互作用过程,各参数的时空分布,如自由电子密度、激光强度和电子温度,在图9 中显示.自由电子密度等于临界密度的位置用白色虚线标出.在飞秒激光与材料相互作用过程中,光致电离促进了后续碰撞电离中种子电子的产生.在飞秒激光的主要影响区域的自由电子吸收激光能量而升温.由于入射激光在空间上呈高斯分布,自由电子密度ne和激光强度I在材料的中心区域很高而在远离中心点时较小.回顾图5 可以看出 130 fs 时刻自由电子密度已经达到了临界密度.因此,出现白色虚线表示此时自由电子密度等于临界密度的位置.I在熔融石英中的分布被强烈地重塑,同时材料的去除和烧蚀坑的形成占主导地位.然后,虚线的位置在半径和深度方向上延伸,不同深度的激光强度的差异是由这些深度之间的等离子体吸收的激光能量造成的.而反射导致材料表面的激光强度与几纳米深度的激光强度不同.由于光学特性的巨大变化,中心区域的激光强度迅速衰减,这减缓了Te的上升,塑造了如图9 所示的Te时空分布.在模拟结束时,烧蚀坑是自由电子密度ne等于临界密度ncr时可以达到的最大尺寸.同时,烧蚀坑也是所有时刻下自由电子密度等于临界密度所在位置的包络线.烧蚀坑的半径约为2.9 µm,这在光学反射率急剧变化的区域半径范围内.结果表明,光学特性在时间和空间上重塑了激光强度分布.此外,强烈重塑的激光强度导致了烧蚀轮廓和电子温度的分布. 图9 脉冲持续时间 tp=120 fs、激光能量密度 F=6.2 J/cm2时,自由电子密度 ne、激光强度 I和电子温度 Te 的时空分布.白色虚线表示 ne=ncr 的位置Fig.9.Spatiotemporal distributions of free electron density ne ,laser intensity Iand free electron temperature Tewithtp=120 fs and F=6.2 J/cm2 .The white dashed lines locate where ne=ncr . 综上所述,本文通过理论和实验研究了飞秒激光加工熔融石英,发现了计算的阈值能量密度和烧蚀深度与实验结果较好吻合[10,22,29,30].本研究证明,激光能量密度和脉冲持续时间主导了自由电子弛豫时间的演变,这对光学反射率和光学穿透深度的巨大变化非常重要.显著变化的光学特性强烈地塑造了激光强度分布,并限制了高激光能量密度下的激光能量吸收,使得烧蚀深度接近饱和,烧蚀效率下降,进而在烧蚀坑底部得到一个平坦的区域.此外,实验中观察到的熔融石英的烧蚀体积与激光能量密度之间的线性关系,通过理论模型仿真计算得到了验证.本文研究证实,使用脉冲持续时间处于数十飞秒到数百飞秒的激光加工,可显著提高深度去除效率和烧蚀效率.该模型可以对给定脉冲持续时间下的烧蚀阈值做出精准预测.在未来飞秒激光加工熔融石英的实际工程应用中,选择 1.4—3.5 倍烧蚀阈值范围内的能量密度,可实现飞秒激光加工效率和能量利用率的迅速提升,但对飞秒激光器输出脉冲能量稳定性的需求也相应提高.而使用高于3.5倍烧蚀阈值的能量密度进行加工时,可获得良好的可重复性加工结果,但加工质量会因为热影响区增大而显著下降.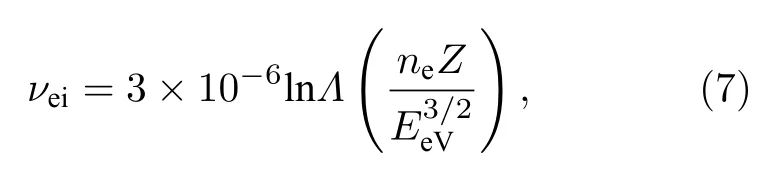
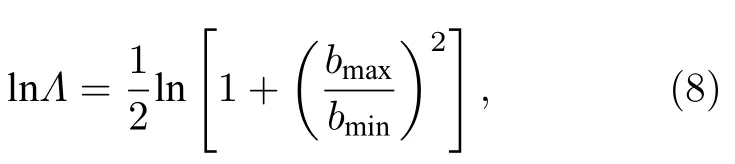
2.3 瞬态光学特性
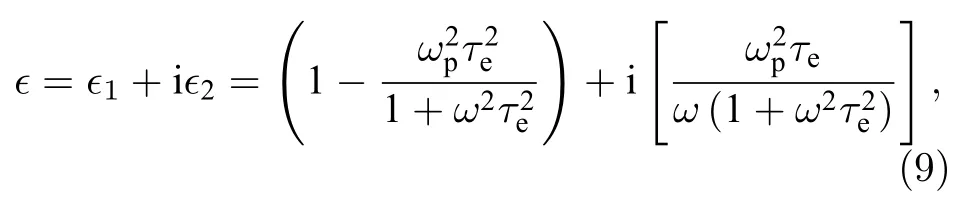

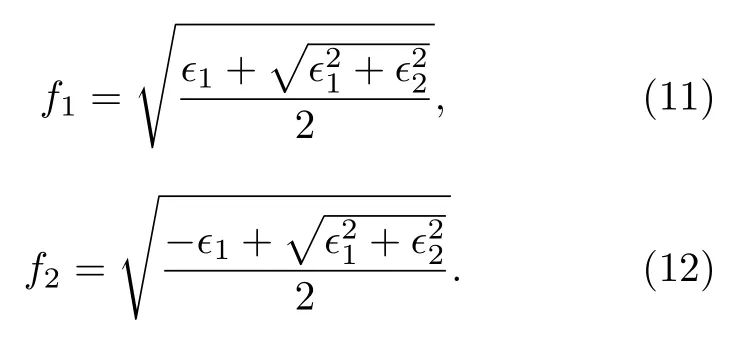
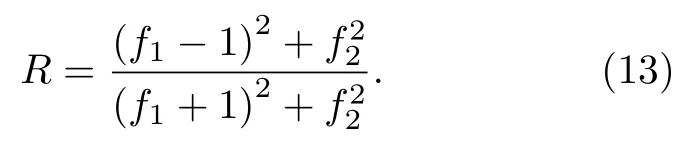
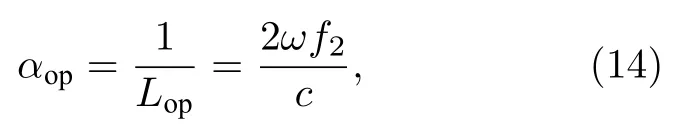
2.4 自由电子温度

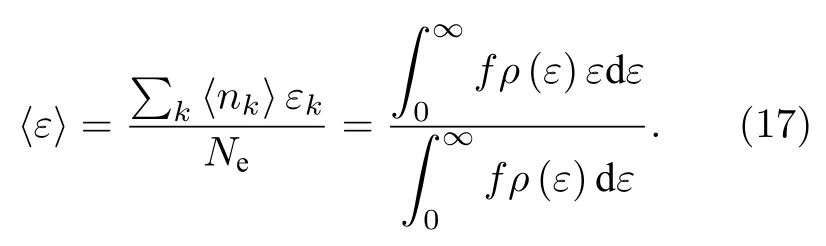
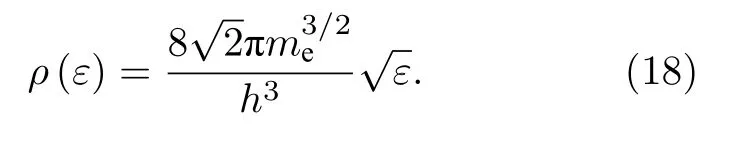
2.5 数值程序
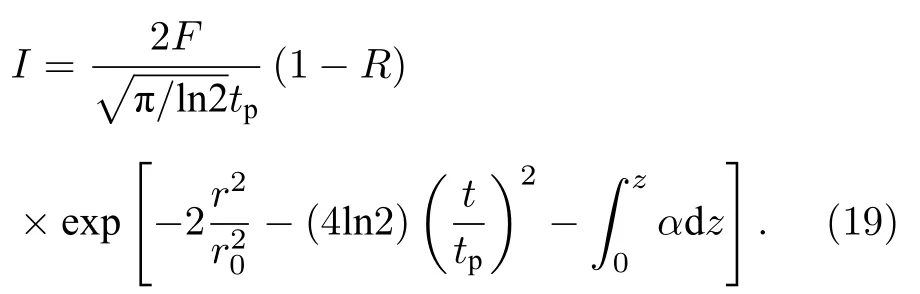
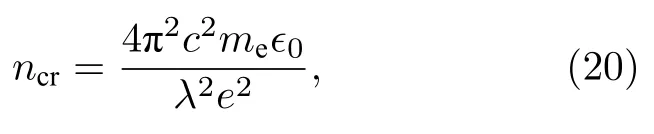
3 实验系统及测量结果
4 讨论部分
4.1 模型验证

4.2 不同激光参数下的电子动态和加工结果
4.3 光学性质、自由电子密度、激光强度和电子温度的时空分布
5 结论
