复合梯度楔形表面上液滴自输运特性的数值研究

高芳，郑佳宜，李准，余延顺

复合梯度楔形表面上液滴自输运特性的数值研究

高芳，郑佳宜，李准，余延顺

（南京理工大学 电子设备热控制工信部重点实验室，南京 210094）

提高表面液滴的自输运速率。在表面引入润湿梯度和楔形形状，基于VOF模型（流体体积模型）对表面液滴运动进行数值研究，并建立一种适用于润湿梯度和楔形图案联合的模型，分析润湿梯度和楔形角度对液滴位移的影响。润湿梯度越大，液滴受不平衡的表面张力越大，液滴移动速度越快。润湿梯度为15 (°)/mm表面上液滴的平均速度比10、5 (°)/mm润湿梯度的表面分别快42.3%和130%。楔角越大，加速阶段的液滴移动速度越快，但会越早失去驱动力而停止移动，而楔角越小，液滴移动位移越大。液滴在40°楔角表面最先停止运动，在20°楔角表面位移比30°和40°楔角表面分别远10.3%和32.3%。联合润湿梯度和楔形图案后，15 (°)/mm表面上的液滴在20°、30°、40°和20°楔角表面上的液滴在15、10 (°)/mm下均能运动到计算模型出口，且15 (°)/mm、40°楔角表面液滴的平均速度达到292 mm/s，比单一梯度表面增长37.7%，比单一楔形图案表面（20°）增长175.5%。通过调节润湿梯度和楔形角度，可有效控制液滴移动速度。联合润湿梯度和楔形图案的复合梯度楔形表面能同时减小润湿性范围瓶颈和楔形形状制约，提高表面液滴的移动速度和距离。研究结果将有助于设计高效的液滴输运功能表面，并可将其扩展到冷凝装置、微流体装置和药物检测等领域。

润湿梯度；界面张力；楔形；自输运；两相流；数值模拟

近年来，许多研究人员试图在不同类型的能量系统（如供暖、通风、空调和制冷系统）中，通过表面润湿性改性来控制液滴的自输运，以此增强冷凝排水[1-4]。因为广泛用于换热器翅片的铝、铜和不锈钢具有天然亲水性，在表面易形成膜状冷凝，增大传热面热阻，降低传热效率[5-6]。因此，传热表面上液滴的管控对系统的整体能效至关重要。液滴的可控自运动在其他领域也具有广泛的应用前景，如微流体装置、雾收集、工业过滤设备等[7-11]。

大量学者根据天然表面（如蜘蛛丝[12-13]和沙漠甲虫[14-16]）的集水功能，引入润湿梯度和楔形图案来驱动液滴在表面上移动。因受到的表面张力不平衡，液滴能在润湿梯度表面上向接触角更小的方向移动。早在1992年，Chaudhury等[17]就在硅表面上制备出表面能梯度，以使液滴能在其上自输运。事实上，为了揭示液滴在润湿梯度表面上定向输运的机理和影响因素，学者已对表面制备及在其上的液滴移动进行了很多试验和模拟研究，并取得了一些进展[18-23]。

楔形图案表面则是利用液滴在表面上因润湿差异性产生变形，形成沿着输运方向的半径差，进而产生具有梯度的拉普拉斯压差，驱动液滴从顶端薄尺寸向底端厚尺寸移动。近年来，制备图案表面的常见方式有等离子溅射法[24]、激光加工法[25]、光刻法[26]、掩模辅助法[27]等。Zhang等[28]将梯形亲水材料图案化到疏水基底上，液滴在表面上自发从梯形的窄端向宽端铺展。Khoo等[29]在超疏水基底上制备出三角形的超亲水轨道，液滴铺展速度达到50～400 mm/s。Alheshibri等[30]用等离子体暴露和HDFT溶液浸泡，使铜表面呈超疏水，而铝呈超亲水，制备铝/铜润湿性图案表面，但液滴的移动距离被限制在30 mm。

润湿梯度表面虽能实现液滴的自输运，但润湿性范围瓶颈导致液滴的移动距离极大受限。楔形图案表面的液滴输运则会受到楔形形状的制约，远距离的输运需要较大的楔形末端尺寸。因此，本研究建立了一种适用于润湿梯度和楔形图案联合的计算模型，并基于VOF模型对表面上的液滴运动进行了数值研究，提供了表面上润湿梯度、楔形图案和2种方式联合的复合梯度楔形表面上液滴自输运的动力学特性观察。研究结果将有助于设计高效的液滴输运功能表面，并可将其扩展到冷凝装置、微流体装置和药物检测等领域。

1 计算模型与方法

1.1 控制方程

VOF模型通过计算不同组分在计算域每个控制体内的体积分数，然后利用插值法来得到各组分间的边界，从而模拟多组分的流动情况。

第个组分在任一单元中的体积分数由式（1）确定：

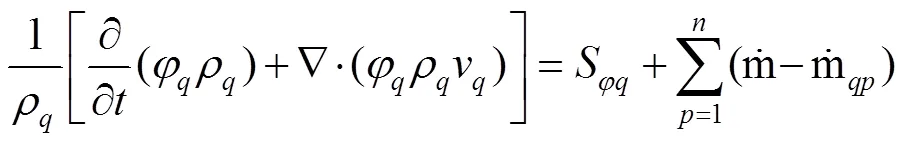
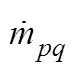
整个计算域中所有组分均服从同一个动量方程：

式中：为密度；为黏度。

考虑表面张力的影响，将CSF（Continuum Surface Force）模型[31]作为源项添加到动量方程中。对于两相流：

式中：σ为组分间的表面张力系数；为截面曲率。

壁面的润湿梯度通过接触角设定，其作用体现在近壁面处流体边界的法线方向上。该法线方向的变化会改变界面的曲率，从而间接影响表面张力的大小。

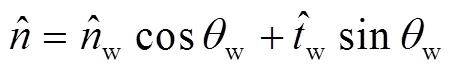
1.2 模型建立

模型的俯视图如图1所示。图1a为润湿梯度表面，表面接触角从90°向右每毫米减小，即相邻不同颜色矩形表面接触角相差。5 mm后，梯度不变，为15°、10°、5°时，表面梯度分别为15、10、5 (°)/mm。图1b为楔形图案表面，灰色区域为接触角160°的超疏水基底，黄色区域为接触角90°的亲水楔形，楔角取20°、30°、40°。图1c为复合梯度楔形表面，灰色区域为接触角160°的超疏水基底，黄色区域为亲水梯度楔形，接触角变化与图1a一致，楔角取值与图1b一致。模型计算区域为一个10 mm×10 mm×5 mm的矩形流体域，初始计算时，在底面上放置一个半径为1 mm的半球形液相区域作为初始液滴图。采用常压出入口，因液滴流速较慢，采用层流模型。为更好捕捉气液界面，采用VOF模型，流体默认常热物性。

液滴在润湿梯度和楔形图案表面上的受力如图2所示。在不平衡表面张力的驱动下，液滴会向润湿梯度表面上的高表面能侧移动。如图2a所示，这种力可用高、低表面能侧的液滴接触角差异表示[32]：

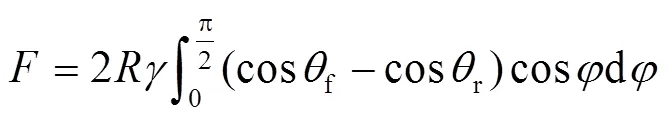
式中：为液滴的半径；为表面张力；f和r为液滴移动方向的前后接触角；为圆柱极坐标系统中的极角，其原点位于液滴轨迹的中心。

楔形图案表面上的楔角是液滴运动的驱动力来源，楔形角度会影响液滴的移动速度和距离。如图2b所示，楔形图案表面上的驱动力由2个不同润湿性表面边界区域上液滴的接触面积确定[33]：

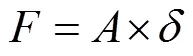
式中：A是常数。

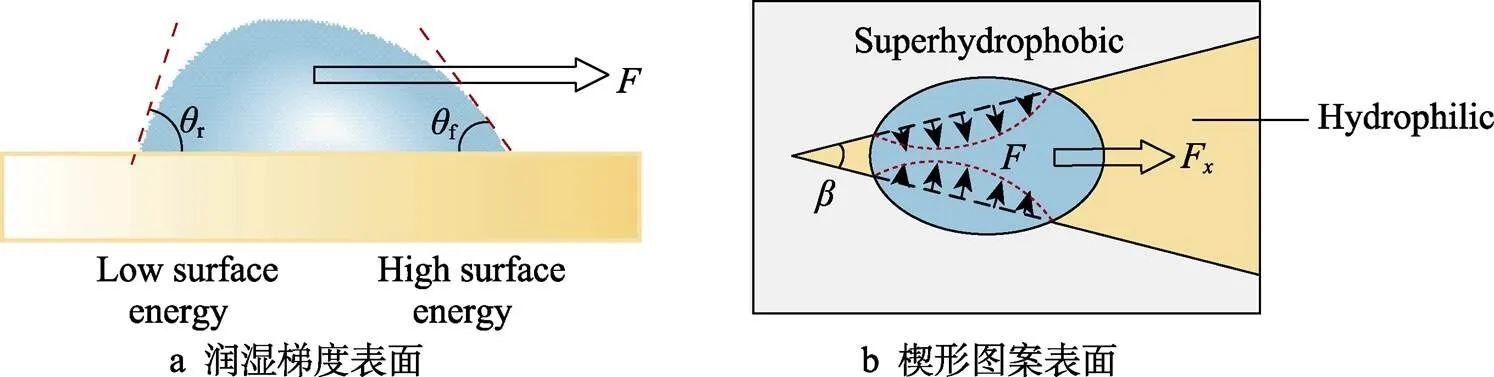
图2 液滴定向移动示意图

由于驱动力的方向与边界垂直，沿方向的驱动力可表示成：

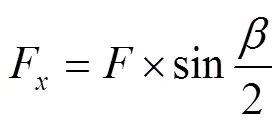
1.3 网格划分及无关性验证

采用非结构性网格对计算与进行离散，并对底面进行边界层加密，液滴流动区域再单独加密。网格的划分质量及精度对数值模拟结果的准确性有很大影响，因此需对不同网格数量进行网格无关性验证。在润湿梯度10 (°)/mm的条件下，分别对网格数为 156 373、333 925、448 366、663 721和789 935的模型进行计算，对比不同网格数量下液滴移动到出口的时间。在网格数为448366、663721和789935时，曲线趋于平缓，因此可认为网格数448 366满足精度要求，如图3所示。

1.4 模型验证

为验证本文提出的数学模型的准确性，将模拟结果与文献[34-35]进行对比。文献[34]采用VOF模型，在长和高分别为10 mm和1.8 mm的带有润湿性梯度的矩形计算域中，滴入半径为0.8 mm的半圆形液滴研究水平润湿梯度表面上梯度大小对液滴运动过程的影响。图4a显示了本模型计算的9 (°)/mm润湿梯度下液滴运动情况与文献[34]中研究结果的对比。结果显示，液滴在各时间下的运动状态基本一致，但模拟结果与文献相比较慢，在0.026 4 s时，模拟结果比文献运动距离减少了0.51 mm。这是由于液滴的驱动主要取决于液滴和壁面的接触区域，在模型底面加密了10层边界层后，由于网格的细化，液滴在更小尺寸内的移动也可被捕捉到，而不会因为网格过大而被忽略，从而对液滴移动的捕捉更加准确，因此可认为润湿梯度模型的数值结果可靠。文献[35]采用格子–玻尔兹曼模型模拟和实验相结合，在亲水区域接触角25°、疏水区域接触角145°的楔形图案表面上研究了楔角大小对液滴移动的影响。图4b显示了本模型计算的楔角15°下液滴运动情况与文献[35]中研究结果的对比。结果显示，液滴在各时间下的运动状态基本一致，因此可认为楔形图案模型的数值结果可靠。

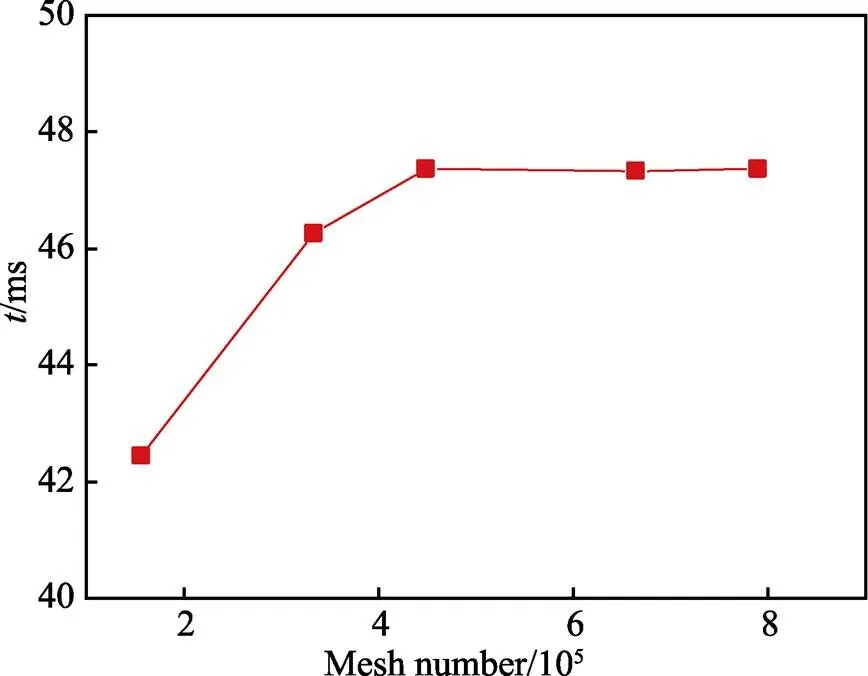
图3 网格无关性验证

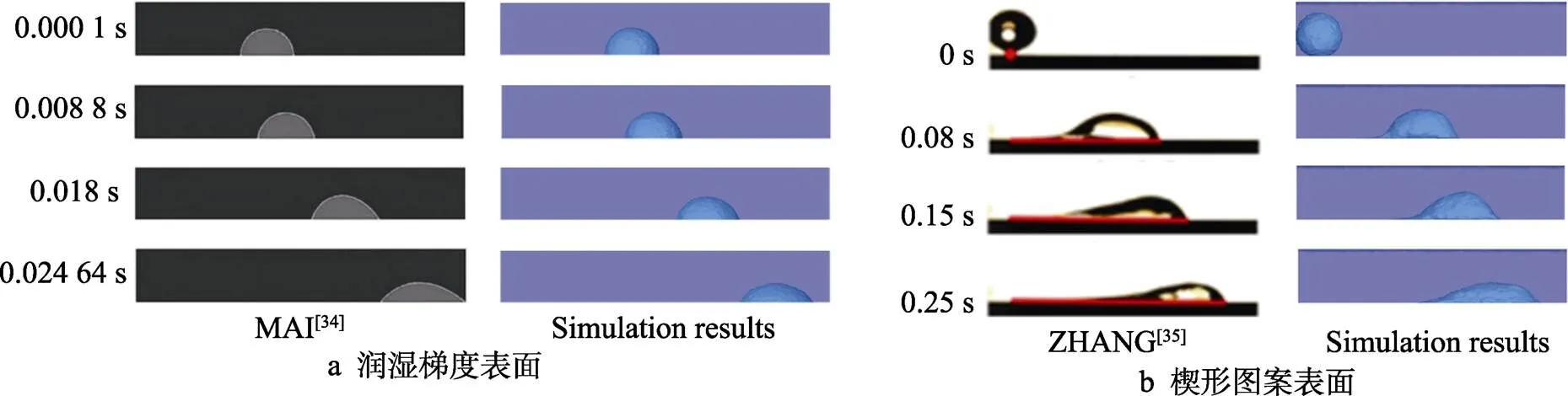
图4 模型验证

2 结果与分析

2.1 润湿梯度对液滴运动的影响

本文研究了半径为1 mm的液滴在15、10、 5 (°)/mm等3个不同润湿梯度表面上的自运动，如图5所示。随着液滴的移动，液滴与表面的接触面积增加，液滴高度降低。液滴运动可分为3个阶段，第一阶段（0～9 ms）如图6a所示，液滴滴落在3个固体表面后开始铺展，15 (°)/mm表面更亲水，液滴高度更低，铺展速度更快。9 ms后，液滴在表面上铺展完成。因不平衡表面张力的出现，液滴开始加速移动。作用在液滴上的不平衡表面张力受液滴两侧接触角的影响，因此润湿梯度越大，表面张力驱动力越大，曲线斜率越大，液滴移动速度越快。15、10、5 (°)/mm表面上液滴分别在17、22、32 ms时达到恒定接触角处（=6 mm），即速度最大处，如图6b所示。第三阶段，由于表面润湿梯度的消失，液滴在到达=6 mm后，在阻力作用下，开始减速移动。5 (°)/mm表面上液滴的初始阶段斜率较小，即初始速度较小，在还未到达计算模型出口（=8.5 mm）时，速度就减至0。15 (°)/mm表面上的润湿梯度更大，初始阶段斜率更大，初始速度更大，因此最先到达计算模型出口。全过程平均速度可达212 mm/s，比10 (°)/mm和5 (°)/mm表面分别快42.3%和130%。

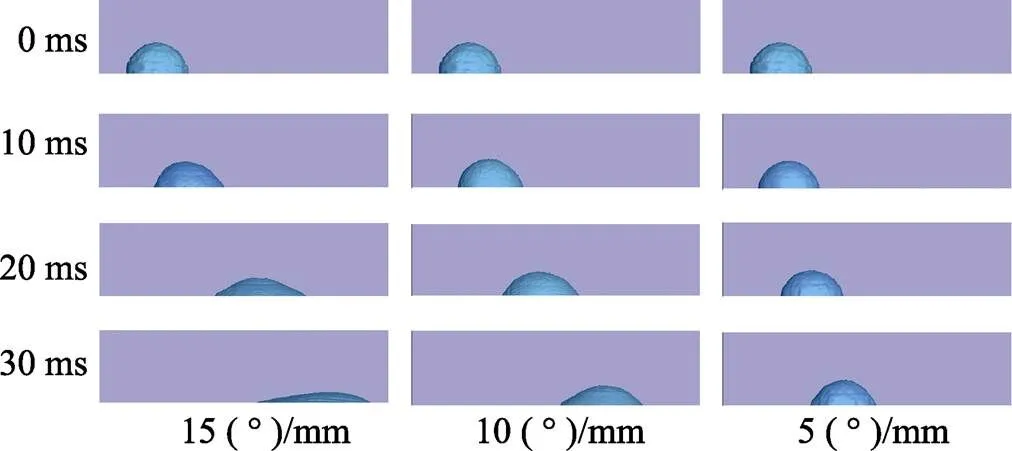
图5 液滴位移随时间变化

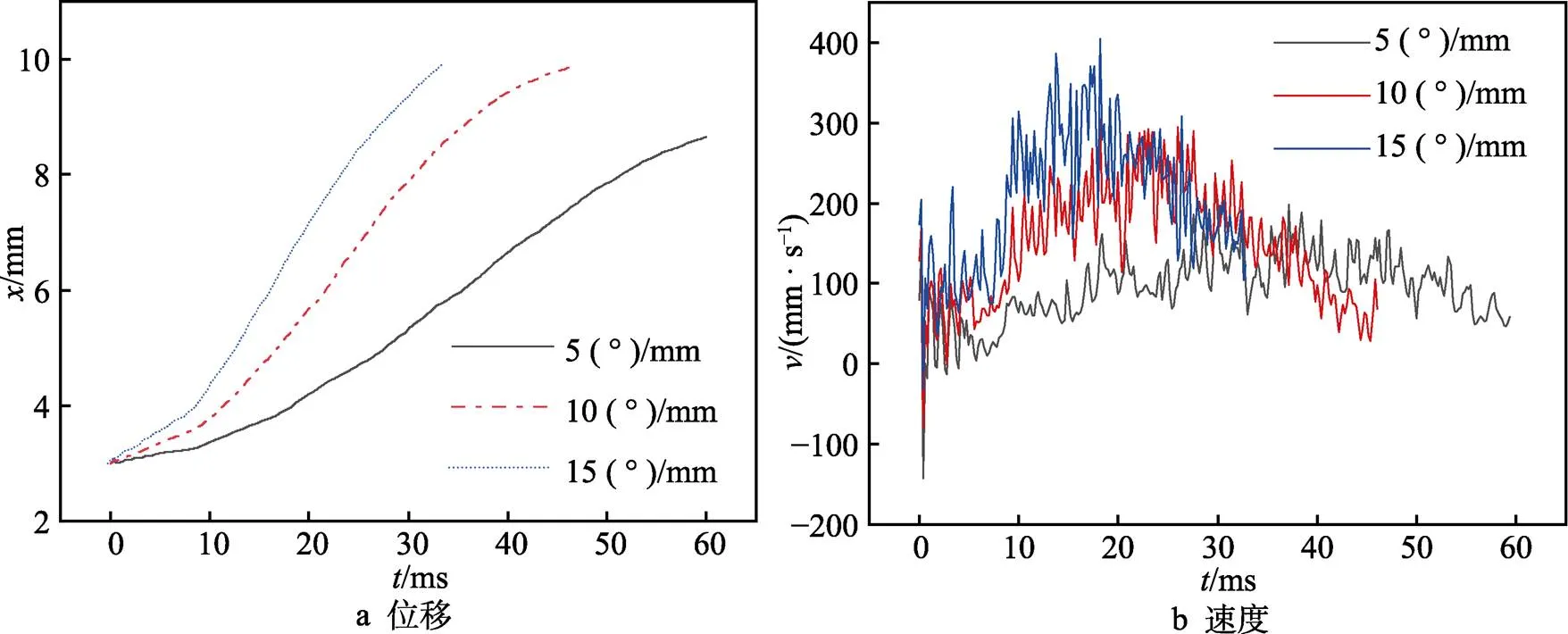
图6 润湿梯度对液滴移动位移和速度的影响

2.2 楔形角度对液滴运动的影响

为研究楔角对液滴移动的影响，在超疏水区160°、亲水区90°的表面上取楔角为20°、30°、40°，对其上液滴的移动规律进行研究。液滴放置在表面后，会逐渐铺展到亲水和疏水区域上。由于楔形内外润湿性不同，且沿流动方向楔形宽度逐渐增大，液滴会自发地向较宽的楔形亲水区域移动。曲线斜率先增大、后减小，即液滴移动速度先增后减，在=20 ms（=20°）、= 18 ms（=30°）和= 14 ms（=40°）时，液滴速度分别达到最大，如图7所示。在加速阶段，表面楔角越大，推动力在液滴移动方向上的分力越大，因此液滴在表面上的速度随楔角的增大而增大。

随着液滴移动，亲水区域宽度逐渐增加，楔角越大的表面在相同位移处亲水区域的宽度越大，液滴越早完全进入亲水区域，从而越早失去向前的驱动力。因此，楔角越大，曲线斜率减小越快，液滴速度下降越快，越早停止移动。如40°楔角表面液滴最先停止运动，20°楔角下，液滴最大位移为8.6 mm，比30°和40°楔角表面分别远10.3%和32.3%。

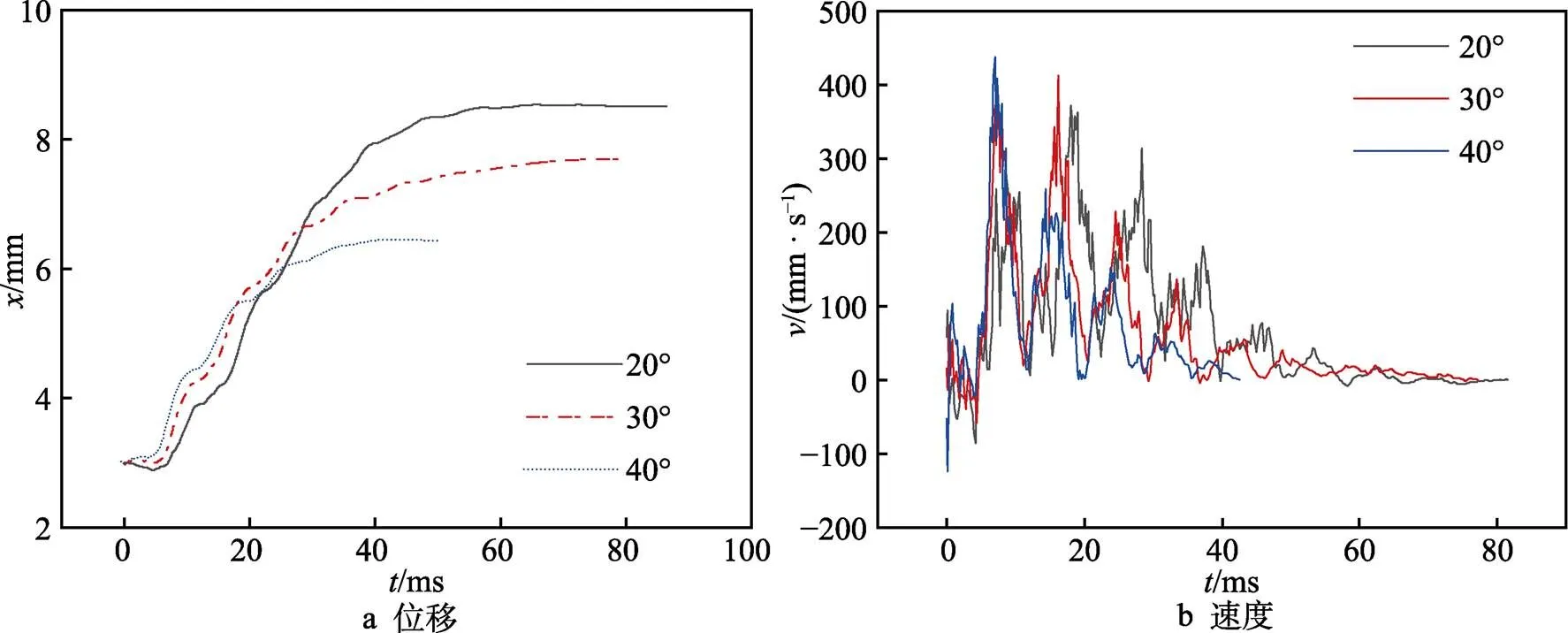
图7 楔形角度对液滴移动位移和速度的影响

2.3 润湿梯度和楔形图案联合对液滴运动的影响

为进一步提高液滴的移动速率和距离，将润湿梯度和楔形图案联合，提出复合梯度楔形表面。如图8所示，在15 (°)/mm润湿梯度和20°楔角下，液滴在复合梯度楔形表面上的整体运动趋势分别与楔形图案表面和润湿梯度表面基本一致。因复合梯度楔形表面增加了楔形图案，在不平衡表面张力和楔角形成的推动力的共同作用下，液滴在复合梯度楔形表面的曲线斜率更大，移动速度更大、距离更远。因此，15 (°)/mm表面上的液滴在20°、30°、40°和20°楔角表面上的液滴在15 (°)/mm和10 (°)/mm下均能运动到计算模型出口，且15 (°)/mm、20°楔角表面液滴的平均速度可达292 mm/s，比单一梯度表面[15 (°)/mm]增长37.7%，比单一楔形图案表面（20°）增长175.5%。

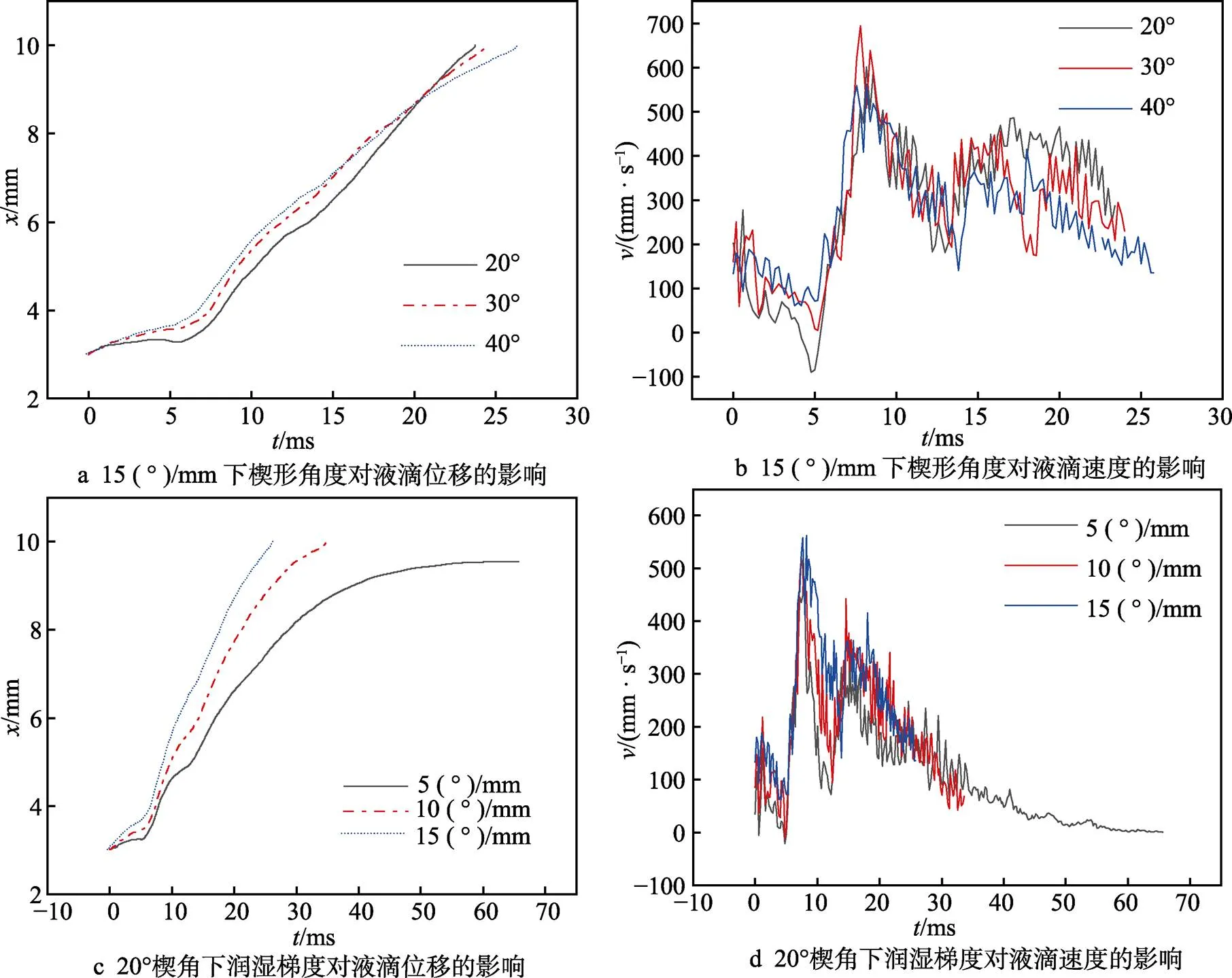
图8 楔形角度和润湿梯度联合对液滴移动的影响

3 结论

本文对液滴在不同润湿梯度和楔形角度表面上的移动进行了数值模拟。模拟结果表明，润湿梯度越大，液滴受不平衡的表面张力越大，液滴移动速度越大。润湿梯度为15(°)/mm表面上液滴的平均速度可达到212 mm/s，比10(°)/mm和5(°)/mm表面分别快42.3%和130%。楔角越大，加速阶段的液滴移动速度越大，但会越早失去驱动力而停止移动，而楔角越小，液滴移动位移越大。液滴在40°楔角表面最先停止运动，在20°楔角表面位移为8.6 mm，比30°和40°楔角表面分别远10.3%和32.3%。联合润湿梯度和楔形图案后，15(°)/mm表面上的液滴在20°、30°、40°和20°楔角表面上的液滴在15(°)/mm和10(°)/mm下均能运动到计算模型出口，且15(°)/mm、40°楔角表面液滴的平均速度达到292 mm/s，比单一梯度表面增长37.7%，比单一楔形图案表面（20°）增长175.5%。

[1] ALWAZZAN M, EGAB K, PENG Ben-li, et al. Cond­ensation on Hybrid-Patterned Copper Tubes (I): Characte­rization of Condensation Heat Transfer[J]. International Journal of Heat and Mass Transfer, 2017, 112: 991-1004.

[2] ALWAZZAN M, EGAB K, PENG Ben-li, et al. Conde­nsation on Hybrid-Patterned Copper Tubes (II): Visualiz­ation Study of Droplet Dynamics[J]. International Journal of Heat and Mass Transfer, 2017, 112: 950-958.

[3] YANG K S, LIN K H, TU Cheng-wei, et al. Experimental Investigation of Moist Air Condensation on Hydrophilic, Hydrophobic, Superhydrophilic, and Hybrid Hydrophobic- Hydrophilic Surfaces[J]. International Journal of Heat and Mass Transfer, 2017, 115: 1032-1041.

[4] PENG Ben-li, MA Xue-hu, LAN Zhong, et al. Experim­ental Investigation on Steam Condensation Heat Transfer Enhancement with Vertically Patterned Hydrophobic- Hydrophilic Hybrid Surfaces[J]. International Journal of Heat and Mass Transfer, 2015, 83: 27-38.

[5] SOMMERS A D, YING J, EID K F. Predicting the Onset of Condensate Droplet Departure from a Vertical Surface Due to Air Flow—Applications to Topographically- Mod­ified, Micro-Grooved Surfaces[J]. Experimental Thermal and Fluid Science, 2012, 40: 38-49.

[6] RAFATI NASR M, FAUCHOUX M, BESANT R W, et al. A Review of Frosting in Air-to-Air Energy Exchangers[J]. Renewable and Sustainable Energy Reviews, 2014, 30: 538-554.

[7] SCHELLENBERGER F, ENCINAS N, VOLLMER D, et al. How Water Advances on Superhydrophobic Surfaces[J]. Physical Review Letters, 2016, 116(9): 096101.

[8] BAI Hao, JU Jie, ZHENG Yong-mei, et al. Functional Fibers with Unique Wettability Inspired by Spider Silks[J]. Advanced Materials, 2012, 24(20): 2786-2791.

[9] AYOIB A, HASHIM U, GOPINATH S C B, et al. Design and Fabrication of PDMS Microfluidics Device for Rapid and Label-Free DNA Detection[J]. Applied Physics A, 2020, 126(3): 1-8.

[10] SUN Ling-yu, BIAN Fei-ka, WANG Yu, et al. Bioins­pired Programmable Wettability Arrays for Droplets Manipulation[J]. Proceedings of the National Academy of Sciences of the United States of America, 2020, 117(9): 4527-4532.

[11] YANG Shao-lin, LI Mao-hui, FANG Guo-li, et al. Flexible Cement-Sand Coated Cotton Fabrics with Superhydro­philic and Underwater Superoleophobic Wettability for the Separation of Water/Oil Mixtures and Oil-in-Water Emulsions[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2021, 608: 125611.

[12] ZHENG Yong-mei, BAI Hao, HUANG Zhong-bing, et al. Directional Water Collection on Wetted Spider Silk[J]. Nature, 2010, 463(7281): 640-643.

[13] VENKATESAN H, CHEN Jian-ming, LIU Hai-yang, et al. A Spider-Capture-Silk-Like Fiber with Extremely High- Volume Directional Water Collection[J]. Advanced Functional Materials, 2020, 30(30): 2002437.

[14] WANG Qiu-yue, YANG Fu-chao, GUO Zhi-guang. The Intrigue of Directional Water Collection Interface: Mech­anisms and Strategies[J]. Journal of Materials Chemistry A, 2021, 9(40): 22729-22758.

[15] LEI Jun, GUO Zhi-guang. A Fog-Collecting Surface Mimicking the Namib Beetle: Its Water Collection Efficiency and Influencing Factors[J]. Nanoscale, 2020, 12(13): 6921-6936.

[16] NØRGAARD T, DACKE M. Fog-Basking Behaviour and Water Collection Efficiency in Namib Desert Darkling Beetles[J]. Frontiers in Zoology, 2010, 7: 23.

[17] CHAUDHURY M K, WHITESIDES G M. How to Make Water Run Uphill[J]. Science, 1992, 256(5063): 1539- 1541.

[18] 原子超, 詹海洋, 刘聪, 等. 浸润性表面液滴定向输运研究进展[J]. 表面技术, 2021, 50(8): 1-17.

YUAN Zi-chao, ZHAN Hai-yang, LIU Cong, et al. Research Progress on Droplet Directional Transport on Wetting Surfaces[J]. Surface Technology, 2021, 50(8): 1-17.

[19] 王鑫, 陈振乾. 梯度润湿表面上液滴定向迁移及合并行为的格子Boltzmann模拟[J]. 计算力学学报, 2019, 36(4): 511-519.

WANG Xin, CHEN Zhen-qian. Simulation of Droplet Directional Migration and Coalescence on Gradient Wetting Surfaces by Lattice Boltzmann Method[J]. Chinese Journal of Computational Mechanics, 2019, 36(4): 511-519.

[20] BAI Fan, LI Yu-ke, ZHANG Hong-na, et al. A Numerical Study on Viscoelastic Droplet Migration on a Solid Substrate Due to Wettability Gradient[J]. Electrophoresis, 2019, 40(6): 851-858.

[21] DIEWALD F, LAUTENSCHLAEGER M P, STEPHAN S, et al. Molecular Dynamics and Phase Field Simulations of Droplets on Surfaces with Wettability Gradient[J]. Computer Methods in Applied Mechanics and Engin­eering, 2020, 361: 112773.

[22] HOU Y P, FENG S L, DAI L M, et al. Droplet Manipu­lation on Wettable Gradient Surfaces with Micro-/Nano- Hierarchical Structure[J]. Chemistry of Materials, 2016, 28(11): 3625-3629.

[23] LU Yang, SHEN Yi-zhou, TAO Jie, et al. Droplet Direct­ional Movement on the Homogeneously Structured Superh­y­drophobic Surface with the Gradient Non-Wetta­bility[J]. Langmuir: The ACS Journal of Surfaces and Colloids, 2020, 36(4): 880-888.

[24] SCHUTZIUS T M, ELSHARKAWY M, TIWARI M K, et al. Surface Tension Confined (STC) Tracks for Capillary- Driven Transport of Low Surface Tension Liquids[J]. Lab on a Chip, 2012, 12(24): 5237-5242.

[25] KOSTAL E, STROJ S, KASEMANN S, et al. Fabrication of Biomimetic Fog-Collecting Superhydrophilic-Superh­ydrophobic Surface Micropatterns Using Femtosecond Lasers[J]. Langmuir: the ACS Journal of Surfaces and Colloids, 2018, 34(9): 2933-2941.

[26] 张倩倩, 漆雪莲, 张会臣. 超疏水结构对AZ91D镁合金微摩擦磨损性能的影响[J]. 表面技术, 2018, 47(11): 102-108.

ZHANG Qian-qian, QI Xue-lian, ZHANG Hui-chen. Effect of Superhydrophobic Structure on Microfriction and Wear Properties of AZ91D Magnesium Alloy[J]. Surface Technology, 2018, 47(11): 102-108.

[27] BAI Hao, WANG Lin, JU Jie, et al. Efficient Water Collection on Integrative Bioinspired Surfaces with Star-Shaped Wettability Patterns[J]. Advanced Materials, 2014, 26(29): 5025-5030.

[28] ZHANG Ji-lin, HAN Yan-chun. Shape-Gradient Comp­osite Surfaces: Water Droplets Move Uphill[J]. Langmuir, 2007, 23(11): 6136-6141.

[29] KHOO H S, TSENG F G. Spontaneous High-Speed Transport of Subnanoliter Water Droplet on Gradient Nanotextured Surfaces[J]. Applied Physics Letters, 2009, 95(6): 063108.

[30] ALHESHIBRI M H, ROGERS N G, SOMMERS A D, et al. Spontaneous Movement of Water Droplets on Patterned Cu and Al Surfaces with Wedge-Shaped Gradients[J]. Applied Physics Letters, 2013, 102(17): 174103.

[31] BRACKBILL J U, KOTHE D B, ZEMACH C. A Continuum Method for Modeling Surface Tension[J]. Journal of Computational Physics, 1992, 100(2): 335-354.

[32] SHEN Chao-qun, LIU Ling-bo, WU Su-chen, et al. Lattice Boltzmann Simulation of Droplet Condensation on a Surface with Wettability Gradient[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2020, 234(7): 1403-1413.

[33] XU Bo, CHEN Zhen-qian. Droplet Movement on a Composite Wedge-Shaped Surface with Multi-Gradients and Different Gravitational Field by Molecular Dyna­mics[J]. Microgravity Science and Technology, 2018, 30(4): 571-579.

[34] 麦彦博, 付宇航, 杨帆. 水平润湿性梯度表面上液滴运动数值模拟[J]. 价值工程, 2016, 35(23): 209-211.

MAI Yan-bo, FU Yu-hang, YANG Fan. Numerical Simulation of Droplet Movement on a Horizontal Wett­ability Gradient Surface[J]. Value Engineering, 2016, 35(23): 209-211.

[35] ZHANG Xiao-yu, HUANG Meng-yu, JI Qian, et al. Lattice Boltzmann Modeling and Experimental Study of Water Droplet Spreading on Wedge-Shaped Pattern Sur­fa­ce[J]. International Journal of Heat and Mass Transfer, 2019, 130: 857-861.

Numerical Study on Droplet Self-transport on Composite Gradient Wedge-shaped Surface

,,,

(MIIT Key Laboratory of Thermal Control of Electronic Equipment, Nanjing University of Science and Technology, Nanjing 210094, China)

The control of droplets on heat transfer surfaces is crucial to the overall energy efficiency of the system, and self-transport of droplets can be controlled by surface wettability modification. Influenced by natural surfaces in nature, many scholars have introduced wetting gradients and wedge patterns to drive droplets to move on surfaces. Although the surface of the wetting gradient can realize the self-transportation of droplets, the bottleneck of the wettability range greatly limits the moving distance of the droplets. Droplet transport on the surface of the wedge pattern is restricted by the shape of the wedge, and larger wedge tip size is required for long-distance transport. This paper aimsto study the directional self-transport of droplets and further improve the self-transport rate of droplets, in addition to introducing wettability gradient and wedge-shape, and the two were combined on the surface. Based on the VOF (volume fluid model)model, a model suitable for the combination of wettability gradient and wedge-shape pattern is used to analyze the effects of wettability gradient and wedge angle on the droplet displacement by numerical simulation. The results show that the moving speed of the droplet can be effectively controlled by adjusting the wetting gradient and wedge angle. The unbalanced surface tension of the droplets increases with the wetting gradient, leading to higher moving velocities. The average velocity of the droplets on the surface with a wettability gradient of 15 (°)/mm was 42.3% and 130% faster than that on the surfaces of 10 (°)/mm and 5 (°)/mm. For larger wedge angle, although the speed of droplet was higher during the acceleration phase, it would stop earlier due to the loss of the driving force.The smaller wedge angle, the greater the displacement of the droplet. The droplet firstlystopped moving on the surface of 40° wedge angle, and the displacement on the surface of 20° wedge angle was 10.3% and 32.3% farther than that on the surface of 30° and 40° wedge angle, respectively. Due to the combination of the wettability gradient and wedge-shape on the composite gradient wedge-shaped surface, under the combined action of the unbalanced surface tension and the driving force formed by the wedge angle, the droplet moves faster and further on the composite gradient wedge surface. After combined wetting gradient and wedge pattern, droplets on 20° wedge angle surface at 15 (°)/mm and 10 (°)/mmcan move to the exit of the calculation model, and the average velocity of the droplet on the surface with 15 (°)/mm and 40° wedge angle reaches 292 mm/s, which is 37.7% higher than that of the single gradient surface and 175.5% higher than that of the single wedge pattern surface (20°).The composite gradient wedge-shaped surface that combined the wettability gradient and the wedge pattern can simultaneously reduce the bottleneck of the wettability range and the wedge shape restriction and improve the moving speed and distance of the droplets. The research results will help design efficient droplet transport functional surfaces and extend the fields of condensing devices, microfluidic devices, and drug detection.

wettability gradient; interfacial tension; wedge-shape; self-transport; two-phase flow; numerical simulation

TQ022.1

A

1001-3660(2022)11-0405-07

10.16490/j.cnki.issn.1001-3660.2022.11.038

2021–11–09；

2022–03–28

2021-11-09；

2022-03-28

国家自然科学基金项目（51706101）

The National Natural Science Foundation of China (51706101)

高芳（1996—），女，硕士研究生，主要研究方向为液滴输运。

GAO Fang (1996-)，Female, Postgraduate, Research focus: droplet transport.

郑佳宜（1986—），女，博士，副教授，主要研究方向为液滴动力学。

ZHENG Jia-yi (1986-), Female, Doctor, Associate professor, Research focus: droplet dynamics.

高芳, 郑佳宜, 李准, 等. 复合梯度楔形表面上液滴自输运特性的数值研究[J]. 表面技术, 2022, 51(11): 405-411.

GAO Fang, ZHENG Jia-yi, LI Zhun, et al. Numerical Study on Droplet Self-transport on Composite Gradient Wedge-shaped Surface[J]. Surface Technology, 2022, 51(11): 405-411.

责任编辑：刘世忠