基于改进粒子群算法的分布式频率分集阵栅瓣抑制方法*
2022-12-30陈炽雄景小荣刘友永陈静金海焱
陈炽雄,景小荣,刘友永,陈静,金海焱
(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.中国电子科技集团公司第54研究所,石家庄 050081;3.电子科技大学 航空航天学院,成都 611731)
0 引 言
常规的频率分集阵(Frequency Diverse Array,FDA)通过在传统相控阵各阵元间引入微小的频率差,实现了其波束指向与距离、角度相关[1]。因此,除了具有相控阵的所有功能特性外,FDA的阵列因子还具有距离依赖性。这使得FDA雷达在目标定位[2-4]、干扰抑制[5-6]、合成孔径雷达成像[7-8]和安全通信[9-10]等领域有广泛的应用。
当前,对于FDA研究,通常假设阵列中阵元间距为半波长,即采用集中式阵列部署[11]。文献[12]在集中式阵列基础上建立了子阵级非线性FDA模型,将均匀线阵(Uniform Linear Array,ULA)划分为互相不重叠且包含相同阵元数的子阵,获得了较好的波束聚焦效果。但是,由于集中式阵列孔径通常比较小,导致所形成的波束角度分辨率过低,难以适应高角度分辨率的应用场景的需求[13]。与集中式阵列部署相比,分布式阵列通过增大阵列口径,可大幅提高角度分辨率并显著提高输出信噪比[13]。但是,分布式阵列将各子阵按等间距布阵将导致严重的栅瓣,从而引起波束指向模糊问题。因此,有效解决栅瓣问题成为分布式FDA技术应用的关键。
目前,针对分布式阵列存在的栅瓣抑制问题的研究大多基于分布式相控阵,提出的方法对目标距离和方位信息的联合估计依然无能为力。为此本文结合FDA的思想,构建了一种基于分布式线性子阵的FDA。在此基础上,为了有效地抑制波束的栅瓣,对粒子群(Particle Swarm Optimization ,PSO)算法进行了改进,给出一种改进的粒子群(Improved Particle Swarm Optimization ,IPSO)算法,通过对分布式FDA中子阵间的基线距离进行优化,不但有效地抑制了栅瓣,而且可获得不错的角度分辨率性能,同时获得了与距离和角度均相关的波束图。仿真结果验证了本文所提方法的有效性与可靠性。
1 分布式频率分集阵结构
如图1所示,由K个均匀线阵构成分布式FDA;各子阵均为由M个全向天线阵元构成的ULA,子阵内的阵元间距d=c/2f0,其中c为光速,f0为中心频率;子阵间的基线距离D远大于子阵孔径(简单起见,先假设各子阵基线距离相等)。设定第k个子阵的辐射频率为


图1 分布式频率分集阵
式中:Δfk为子阵k的频率相对于分布式FDA的中心频率的频率增量。
在远场条件下,天线的发射波形即可视为平面波。以子阵1的第1个阵元作为参考阵元,记Rk,1为子阵k中第1个阵元到达远场(θ,Rk,1)处的距离,其中k=1,2,…,K,则

忽略信号随距离衰减的影响,令子阵k中发射信号sk(t)=exp(-j2πfkt),则子阵k发送信号在远场(θ,Rk,1)处合成信号可表示为

式中:wk,m表示子阵k中第m个阵元的发射加权系数。由于Δfk<<c,式(3)中Δfk((k-1)Dsinθ+(m-1)dsinθ)/c≈0,于是,式(3)可写为
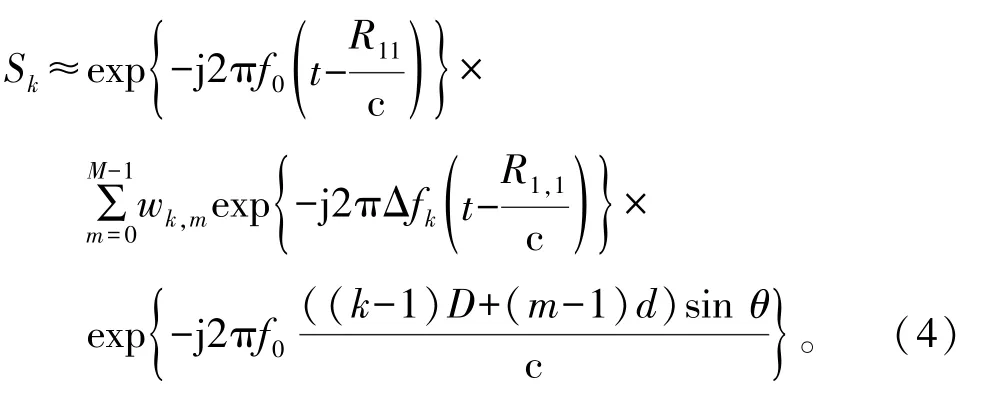
考虑静态波束,即设定t=0。为了使得各子阵发射波束在远场(θ0,R0)处聚焦,加权系数可设计为

由式(4)和式(5)知,K个子阵在远场目标位置(θ0,R0)处合成的信号为
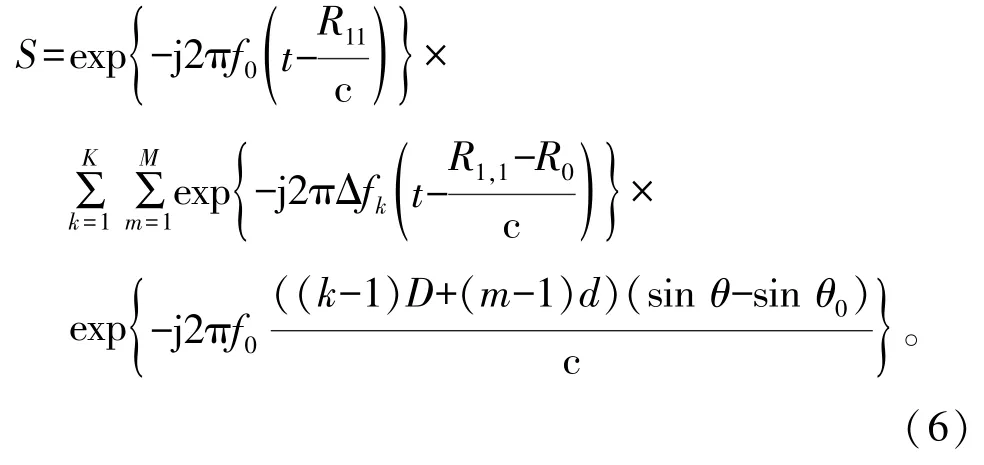
对应地,分布式FDA的发射波束为
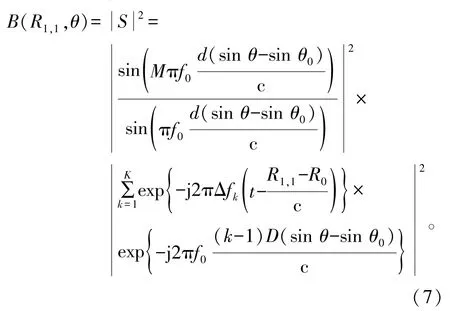
由式(7)知,波束形状与子阵位置密切相关,而子阵间均匀的基线距离会造成大量的栅瓣。为此,下节给出一种IPSO算法来实现栅瓣抑制。
2 改进粒子群算法
PSO是一种基于群体搜索的处理连续或者离散空间内优化问题的算法。为了防止陷入局部最优,根据文献[14],对传统的PSO进行了改进,在下一节将其用于子阵间基线距离的优化,从而实现分布式FDA的栅瓣抑制。
(1)改进1:权重系数w从最大值wmax非线性递减到最小值wmin。w随算法迭代次数的变化公式为[15]
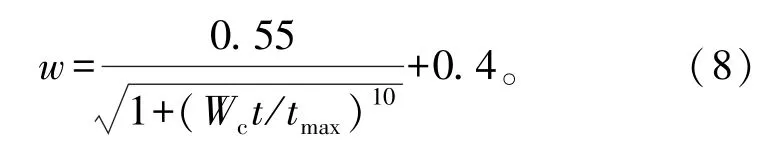
式中:t和tmax分别为算法当前迭代次数和最大迭代次数。通常取wmax=0.95,wmin=0.4。式(8)中的常数0.55和0.4是为了在算法迭代开始取w最大值wmax,而随着迭代次数的增加,w逐渐趋近最小值wmin。这样能够保证粒子群在初始状态时以较大的权重系数进行全局性搜索,而在迭代后期又以较小的固定权值进行更为精细化的局部寻优。Wc为权重控制系数,通过调节Wc的大小进而来调整wmax在种群进化过程中所占的比例。在常规的PSO算法中,Wc通常取3~8之间的整数。为了提高算法迭代前期粒子的全局性搜索能力,本文中选取Wc=3。
(2)改进2:为了提高群体的多样性[15],引入二阶振荡方式对粒子的速度进行更新:
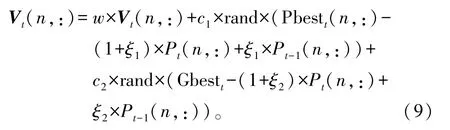
式中:Vt(n,:)、Pbestt(n,:)、Pt(n,:)和Gbestt分别为第t次迭代中第n个粒子的速度、历史个体最优位置、当前位置和群体最优位置;Pt-1(n,:)为第t-1次迭代中第n个粒子的位置;c1、c2为学习因子;rand表示0~1之间的随机数;ξ1、ξ2为随机数,在迭代前期取

这样可以提高粒子在前期的快速寻优能力;在算法后期取
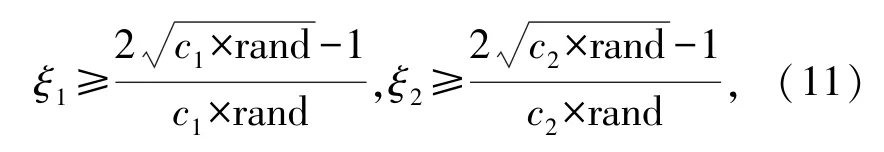
这样可以使得算法渐近收敛。
(3)改进3:引入自然选择原理,在每次迭代过程中将整个粒子群按照适应值的大小来进行排序,并用群体中适应值最好的一半粒子的速度与位置来替换群体中适应值最差的一半粒子的位置和速度,在这一过程中保留原来个体记忆的最优值不变,从而提高粒子接近最优值的几率。
3 分布式FDA栅瓣抑制
由于分布式FDA中各子阵内天线单元间距固定为半波长,因而无法对子阵内各天线单元间距进行优化。为此,通过优化其他子阵的上下边界位置来确定各子阵的最优位置(k-1)Dk,进而实现栅瓣抑制,其中,Dk∈ΔD,ΔD={D1,D2,…,DK}。于是,根据式(7),分布式FDA的发射波束可改写为
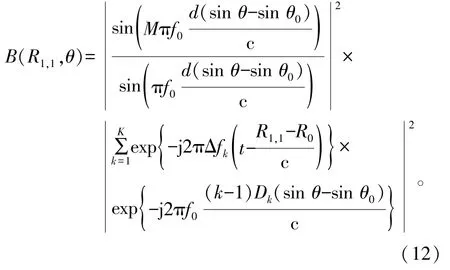
3.1 适应度函数
为了利用IPSO算法对各子阵的位置进行优化,定义适应度函数,其定义为距离维和角度维波束图最大副瓣电平的绝对值之和:

式中:Z1、Z2分别是距离维和角度维波束图的旁瓣区间。定义如下优化模型:
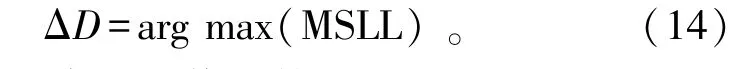
式中:max表示求最大值函数。
3.2 基于IPSO的分布式FDA栅瓣抑制方法的具体操作流程
结合第2节的IPSO,基于IPSO的分布式FDA栅瓣抑制方法的具体操作流程如下(其中,N为IPSO算法迭代过程中粒子的个数,群体最优位置Gbest为式(14)中待求解的ΔD):
输入:N,K,tmax
输出:Gbest
Step 1 初始化粒子的位置矩阵P和速度矩阵V。
1 for alln=1,2,…,Ndo
2P(n,:)=Dmin+(Dmax-Dmin)×rand(1,K)
3V(n,:)=Dmin+(Dmax-Dmin)×rand(1,K)
4 end for
Step 2 计算适应度值,找到Pbest和Gbest。
5 for alln=1,2,…,Ndo
6 compute MSLL

7 end for
8 generating Pbest and Gbest based on MSLL
Step 3 Pbest和Gbest迭代更新。
9 Whilet≤tmaxdo
10 forn=1,2,…,Ndo
11 updateV(n,:) through Second order oscillationmethod
12 updateP(n,:) byV(n,:)
13 end for
14 forn=1,2,…,Ndo
15 compute MSLL

16 end for
17 forn=1,2,…,Ndo
18 update Pbest(n,:) and Gbest based on MSLL
19 end for
20 updatePandVthrough principle of natural selection
21t=t+1
22 end while
由上述流程可知,IPSO算法的复杂度为O(tmax(N+NK+N+NlnN)),PSO的复杂度为O(tmax(N+NK+N))。IPSO算法因其引入的自然选择原理需要在每一次算法迭代中对适应度值进行排序,故而其复杂度略高于PSO。
4 分布式FDA的CRLB分析
克拉美罗下界(Cramer-Rao Lower Bound ,CRLB)作为评估估计性能的重要指标,文献[16]对FDA的CRLB推导和分析进行了深入研究。本节主要对优化后的分布式FDA进行参数估计的CRLB推导。由图1可以推出,当处于时刻t时,参考阵元发出的信号在远场(θ,R1,1)处的相位为

子阵k中第m个阵元发出的信号在远场(θ,R1,1)处的相位为
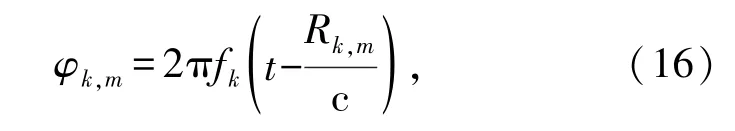
两者相位差表示为

由式(2)、式(15)和式(16),相位差可简化为
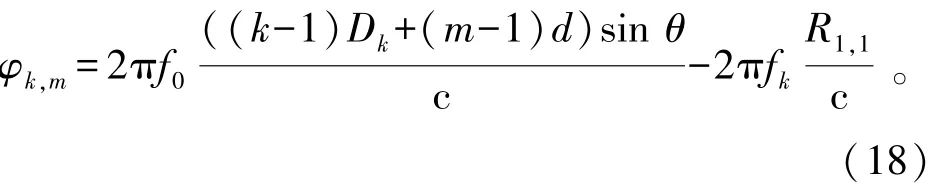
而由式(18),分布式FDA的阵列导向矢量为
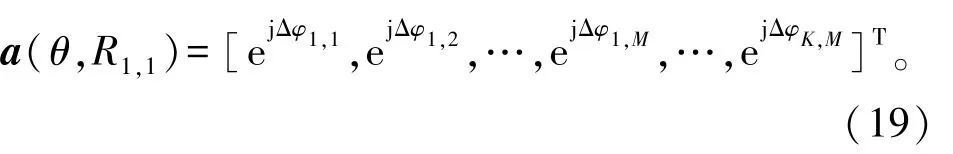
假设目标位于(θ,R1,1),阵列接收到回波信号经过匹配滤波之后,等效的复基带信号可以表示为
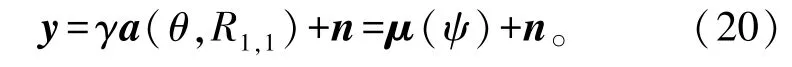
式中:γ表示目标点的反射系数,对于确定的目标γ是一个常数;ψ=[θ,R1,1]T;n为均值为0、方差为σ2的空间复高斯噪声,其协方差矩阵表示为

式中:E{·}表示求数学期望;H表示共轭转置;Rn和σ2分别表示噪声的协方差矩阵和功率;IKM表示KM×KM的单位阵。
当目标的距离R1,1已知而方位角θ未知时,待估计的参数ψ=θ,其费歇尔信息矩阵(Fisher Information Matrix,FIM)定义为

式中:Re{·}表示取信号的实部;ψi表示参数向量的第i个元素;Dψi(ψ)表示为

将式(19)代入式(23),得到

式中:G是一对角矩阵,表示为

信噪 比(Signal-to-Noise Ratio,SNR)定 义 为,于是式(22)可表示为
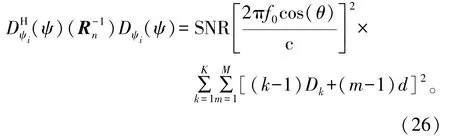
当目标的方位角θ已知而距离R1,1未知时,估计的参数ψ=R1,1,则得到
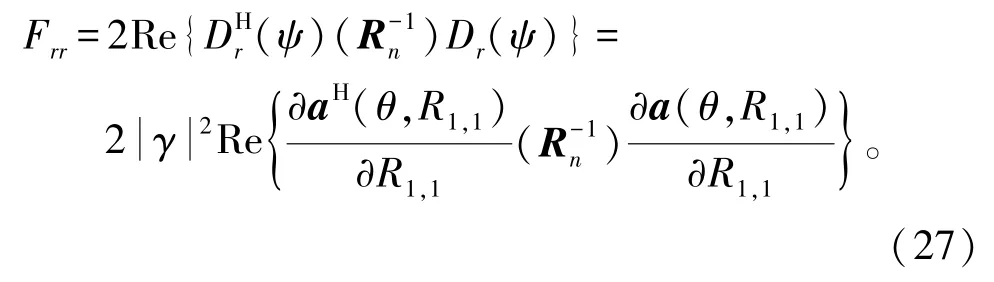
由微积分得到

将式(28)代入式(27)可得
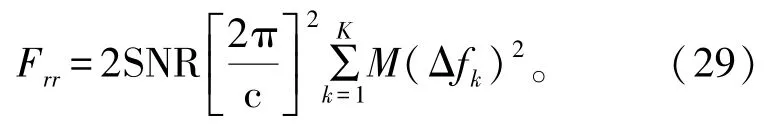
式中:

当目标的距离和方位角均未知时,估计参数ψ=(θ,R1,1),对应的FIM为一个二维的矩阵:

由于

由式(24),式(28)和式(32)得到

将式(33)代入式(31),得到
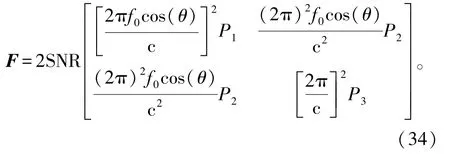
由式(34)可得到
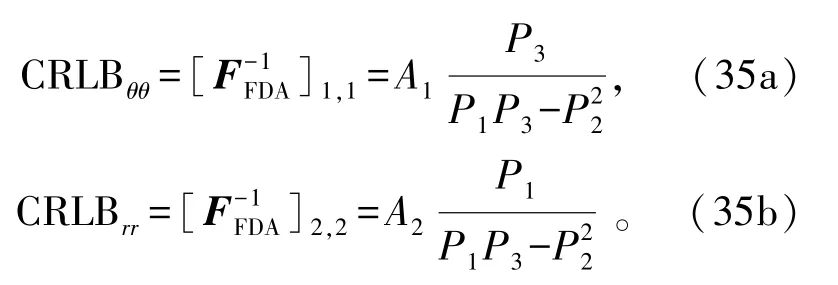
式中:


5 仿真分析
仿真中,设定粒子数N=30,算法迭代次数tmax=1 000;子阵个数K=21,每个子阵的阵元数M=5;Δfk=Δflg(k),频率增量Δf=10 kHz,光速c=3×
108m/s,中心频率f0=10 GHz;粒子速度上限Vmax=1.5,粒子速度下限Vmin=-1.5,粒子位置上限Xmax=1.5 m,粒子位置下限Xmin=1 m;期望目标R0=186 km,θ0=25.20。
5.1 IPSO算法收敛特性
本文提出的IPSO由于引入了第2节中所述的3个改进点,平衡了算法的全局搜索能力和局部搜索能力,提高了群体的多样性,增加了粒子接近最优值的几率,获得了较好的收敛性能。IPSO优化后的子阵位置如表1所示。同时,由收敛速度的定义(式(37))结合图2的仿真结果可知,CIPSO=0.996 5,CPSO=0.998 2。显然,PSO的收敛速度大于IPSO,导致其提前收敛进入局部最优解,这点恰好与图2结果一致。同时,虽然IPSO的复杂度略高于PSO的复杂度,但IPSO算法的寻最优解能力优于文献[14]的PSO算法。

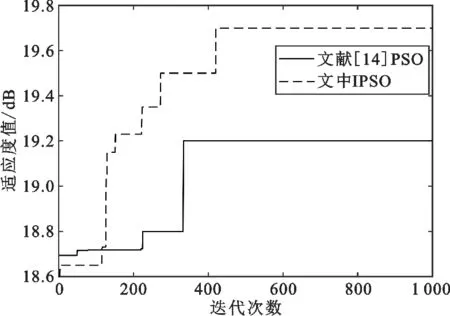
图2 优化过程

表1 参数优化结果
式中:x*是算法迭代收敛值;x(t)表示第t次迭代的数值;C是常数。
5.2 发射波束图解耦及其栅瓣抑制
在分布式FDA中分别采用线性频率偏移和对数频率偏移两种方案,即分别使Δfk=(k-1)Δf和Δfk=Δflg(k),并代入PSO和IPSO优化得到的基线距离参数ΔD。仿真得到栅瓣抑制前后的分布式FDA的发射波束如图3~9所示。
从图3(a)可以看出,各子阵等间距布阵情况下,分布式FDA的线性频偏方案中波束方向图在距离维度出现了严重的栅瓣;然而,图3(b)中的对数频偏方案中却因为打破了波束方向图在距离维的周期性而消除了栅瓣,但是副瓣电平极高。

图3 栅瓣抑制前不同频率偏移方案下的距离维发射波束图
从图4(a)和(b)分析可以发现,各子阵按非均匀方式布阵后,分布式FDA的线性频偏方案中波束方向图在距离维度出现了周期性的峰值,其周期TR=c/Δf。这也验证了其波束方向图在距离维呈现周期性的结论。其次,对于线性频偏方案而言,由于距离-角度耦合问题未得到解决,通过改变子阵的位置对分布式FDA在距离维形成的波束图几乎没有影响。最后,由于对数频偏方案中波束图解除了距离和方位角耦合,所以图4(c)和(d)中消除了栅瓣,波束有且仅有一个峰值,能量更加集中在了特定的区域之内,并且IPSO相比PSO实现了旁瓣的进一步抑制。

图4 栅瓣抑制后不同算法下的距离维发射波束图
由于频率偏移方案的改变对角度维的波束方向图影响不大[17],因此,图5中各子阵等间距布阵情况下,无论是线性频偏方案还是对数频偏方案,分布式FDA的波束方向图在角度维度都会出现严重的栅瓣。
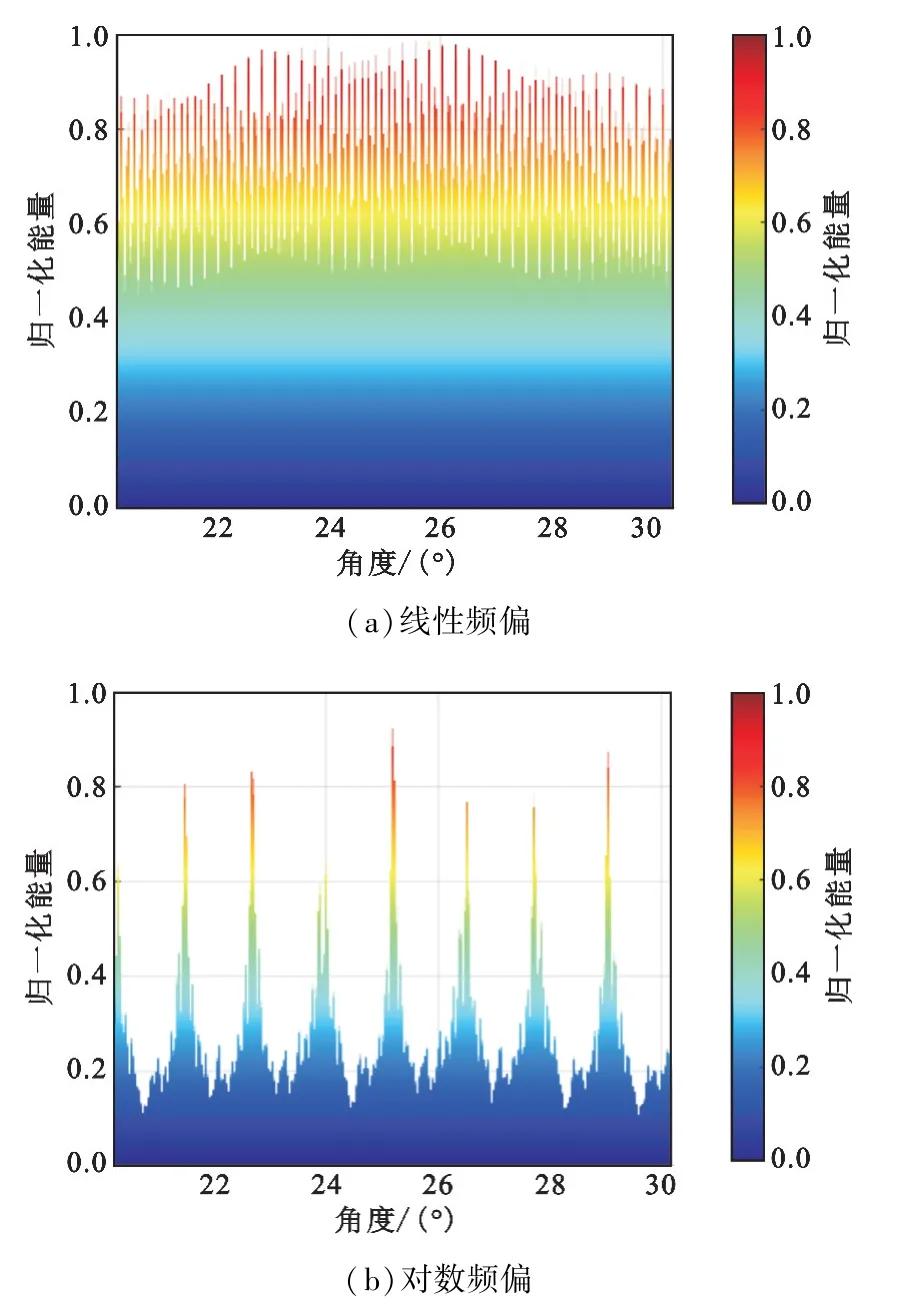
图5 栅瓣抑制前不同频率偏移方案下的角度维发射波束图
由图6~9可看出,各子阵按非均匀方式布阵后,分布式FDA的角度维波束图在两种频偏方案下都消除了栅瓣。在归一化后,IPSO在分布式FDA的角度维波束图的旁瓣抑制中比使用PSO要低0.04左右,旁瓣抑制效果更好。同时,两种频偏方案下的角度维波束宽度都变的很窄,达到了0.06°,大幅提高了角度分辨率,将会使波束指向性更好,使扫描更加精确,从而更有助于目标定位。

图6 PSO线性频偏

图7 IPSO线性频偏
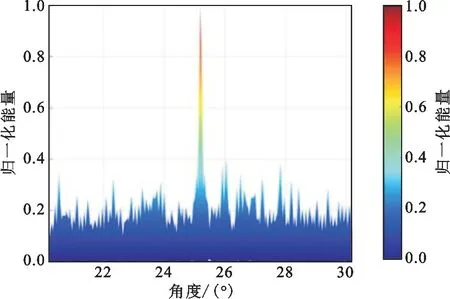
图8 PSO对数频偏

图9 IPSO对数频偏
5.3 分布式FDA的CRLB仿真分析
图10比较了当目标距离和角度均未知时分布式FDA的CRLB性能。首先,可看出使用对数频偏方案下的距离维和角度维估计性能的CRLB均优于使用线性频偏方案,这是因为对数频偏方案打破了距离-角度的耦合性。其次,IPSO下的两种频偏方案下的估计性能均优于PSO。最后,由于分布式FDA角度维较窄的波束宽度,使得角度维的估计性能即使在低信噪比时也比文献[16]有大幅提升。因此本文提出的分布式FDA更加适合应用于对角度分辨率和测角精度要求高的应用场景。
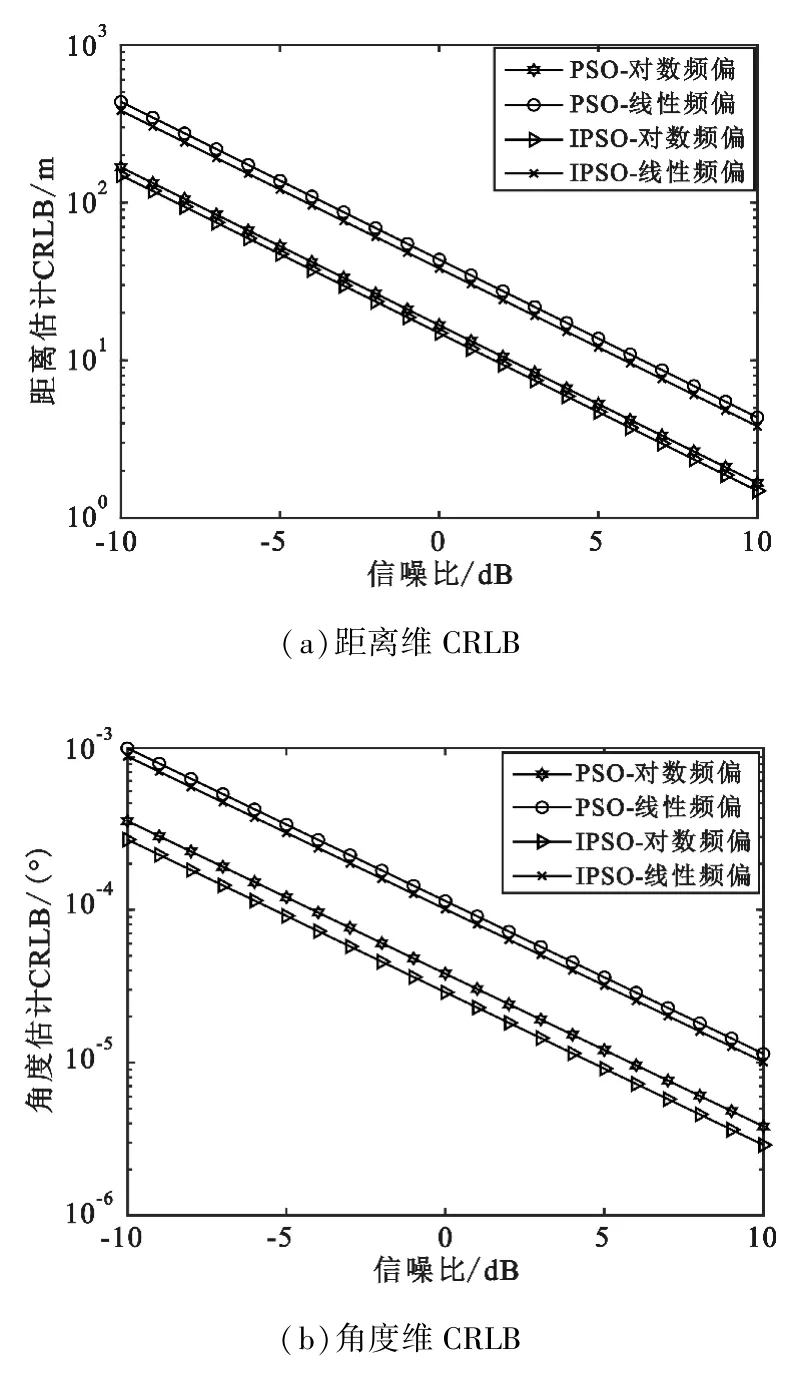
图10 CRLB与SNR的关系
6 结束语
本文融合ULA和FDA,提出了一种基于分布式线性阵列的FDA结构,并通过引入IPSO算法来优化各子阵间的基线距离,以达到消除栅瓣和降低旁瓣的目标;同时,通过理论分析,验证了本文提出的方法可有效提高角度维和距离维的估计性能,从而更有利于目标定位。此外,本文所引入的IPSO算法可推广至其他阵列天线优化设计问题。对于分布式FDA下的多个动目标进行距离-角度-速度的三维参数联合估计性能以及以均匀面阵作为子阵的分布式FDA,将在后续工作中开展研究。
