IGWO-SVM在火控系统故障预测中的应用
2022-12-30李英顺周通刘海洋姚兆田宇
李英顺,周通,刘海洋,姚兆,田宇
(1.北京石油化工学院 信息工程学院,北京 102617;2.沈阳顺义科技有限公司,辽宁 沈阳 110000;3.陆军装甲兵学院 士官学校,吉林 长春 130117)
炮控箱是炮控系统的心脏,通过电缆与其他部件相连,用以完成对炮控系统的启动、调整、控制、工况转换和显示等工作,同时火控系统也是通过炮控箱作用于炮控系统。炮控箱具有使用频率高、发生故障概率高的问题,对炮控箱进行故障预测,可以减轻现场人员维修压力,减少装备维护成本,具有重要的现实意义[1]。
目前,D-S证据融合诊断、BP神经网络、支持向量数据描述[2]、通过机器学习优化支持向量机[3-5]等一系列方法已经应用于故障诊断领域。D-S证据融合诊断方法过于依赖专家系统,具有获取知识困难,知识不完整,适应差等问题[6]。当输入的数据数量多且复杂时,BP神经网络会出现泛化能力差、预测精准度忽高忽低的现象,同时难以解决高维问题[7]。支持向量机(Support Vector Machine,SVM)可以克服样本少的难题,同时可以解决非线性高维问题,具有很强的推广性。
虽然SVM已经广泛运用于故障预测中,但如何选取SVM中惩罚因子C与核参数g成为了制约其发展的重要因素[8]。文献[9]中利用遗传算法高效、鲁棒性强的优点对SVM的参数进行了优化。文献[10-11]中使用灰狼算法参照自然界中灰狼的狩猎过程优化SVM参数,有效提高了分类预测精度。虽然灰狼算法在为支持向量机寻优性能方面有了一定的提高,但存在着求解精度低、易陷入局部最优等问题,还需要更深入的研究,因此笔者提出了改进搜索策略的灰狼算法[12-13]。
随着火控系统组成和结构的日趋复杂,所需检测数据逐渐变多,因此进行特征提取和故障预测愈发困难。由于诊断对象工作复杂、影响因素多,故障出现往往是由多个因素引起的,直接利用传感器数据很难满足诊断预测[14]。针对火控系统测试信号成分复杂、数据量少的问题,笔者提出一种灰色关联度分析的方法,通过计算被测对象各种故障模式对不同类型数据的依赖程度,来降低诊断模块输入维数、简化拓扑结构[15],筛选出具有高关联度的关键影响因素并结合实际关键因素构建数据集[16-18]。利用基于DLH搜索策略改进的灰狼搜索算法优化支持向量机的相关参数,训练集训练完成后,对测试集进行预测验证。
1 算法设计
1.1 灰色关联度分析
1)确定参考序列和比较序列。其分别表示系统行为特征的序列和影响系统行为的因素序列。
2)归一化处理。由于同一个因素序列的量级差别不大,所以通过除以初值将序列进行归一化处理:
(1)
式中:m为序列个数;n为每个序列的数据维度。
3)计算灰色关联系数ξ:

(2)
式中,ρ为分辨系数,ρ>0,且ρ越小分辨力越大,一般取0.5。
4)求关联度ri:
(3)
5)进行关联度排序。
1.2 支持向量机
设n维m组输入样本为
其中设Xi=(x1,x2,…,xi,…,xn)由n个影响特征序列构成,yi为xi与之对应的输出值,SVM把n维数据通过某一线性函数K(x)映射到大于n维的高维空间中,则分类函数可以构建为
f(x)=ωTK(xi)+b,
(4)
式中:ω为超平面的权值向量;b为偏置项。
建立优化目标函数与约束条件,数学表达式如下:
(5)
(6)
式中:C>0为惩罚因子;K(xi)为核函数;ξ为松弛变量。
核函数表达式为
(7)
将式(7)和(8)代入式(4)变形整理,可得支持向量机的最优分类函数为
(8)
式中,αi为拉格朗日乘子。
1.3 改进搜索策略的灰狼算法
1.3.1 灰狼优化算法
灰狼优化算法(Grey Wolf Optimizer,GWO)启动阶段,首先计算出灰狼个体的适应度,之后按适应度进行排序,然后对灰狼种群进行分层。
灰狼分散开来搜寻猎物位置信息,根据适应度最好的3只狼α、β、δ的指挥来确定猎物出现的区域。灰狼搜索、包围猎物的行为可以通过下列数学模型表示:
D=|C·XP(t)-X(t)|,
(9)
X(t+1)=XP(t)-A·D,
(10)
式中:t为迭代次数;A和C为协同系数向量;XP为猎物位置向量;X为当前灰狼位置向量。通过下式计算出向量和:
A=2a·r1-a(t),
(11)
C=2·r2,
(12)
式中:r1和r2是随机向量,取值范围为(0,1);a由2线性降到0,公式如下:
a(t)=2-(2×t)/tMax,
(13)
式中,tMax为最大迭代次数。
每次迭代之后,将计算出适应度最高的3只灰狼保留,作为下一代的α、β、δ狼,由它们来指导搜索灰狼出现的位置区域。该数学模型可以表示为
(14)
(15)
(16)
式中:Xα为α狼的位置;Xβ为β狼的位置;Xδ为δ狼的位置;Dα为当前灰狼与α狼的距离;Dβ为当前灰狼与β狼的距离;Dδ为当前灰狼与δ狼的距离。
在攻击猎物时,候选灰狼的位置会出现在引导灰狼与猎物之间,之后更新下一刻最优灰狼的位置,直至迭代完成。
1.3.2 改进的灰狼算法
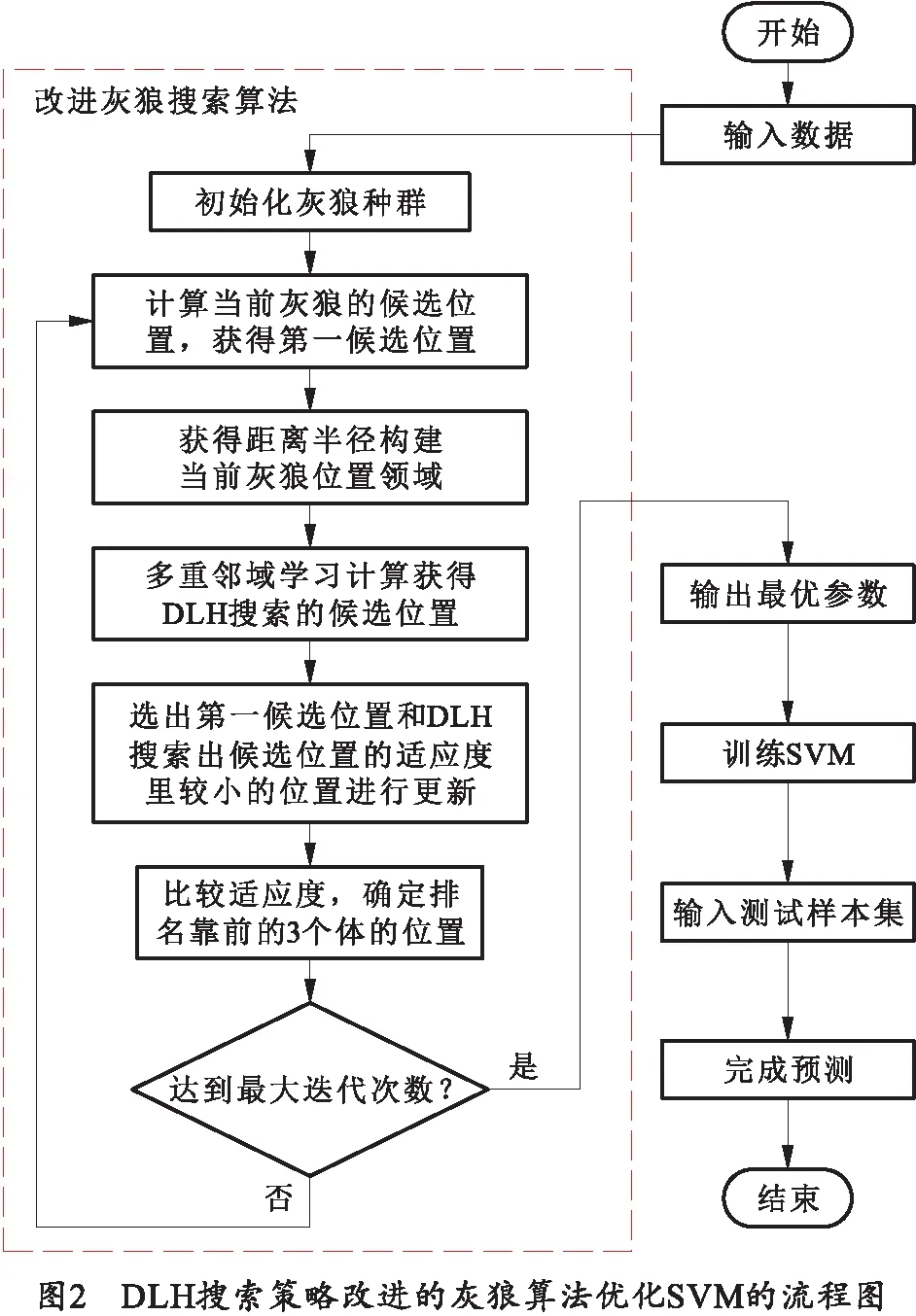
改进的灰狼算法(Improved Grey Wolf Optimizer,I-GWO)得益于一种新的运动策略,基于维度学习的狩猎(Dimension Learning-Based Hunting,DLH)搜索策略。DLH搜索策略为每只狼构建邻域,可以增强局部和全局搜索能力,收敛速度比GWO更快。
I-GWO通过改进选择和更新步骤,形成一个新的搜索策略,其包括初始化、移动以及选择和更新。I-GWO算法流程图如图1所示。

1)初始化阶段。将N只灰狼随机分布在指定的范围(li,uj)内进行搜索,第i只灰狼在第t次迭代中的位置向量表示为Xi(t)={Xi1,Xi2,…,XiD},且
Xij=lj+randj(0,1)×(uj-lj),i∈(1,N);j∈(1,D),
(17)
式中:D为向量的维数;N为狼群矩阵Pop的行数。
2)运动阶段。I-GWO首先通过常规GWO搜索策略,将计算出的灰狼候选位置作为第一候选位置Xi-GWO(t+1),然后采用DLH搜索策略计算出另一新的候选位置Xi-DLH(t+1)。
在DLH搜索策略中,首先计算当前灰狼位置Xi(t)与第一候选位置Xi-GWO(t+1)之间的欧氏距离Ri(t):
(18)
以Ri(t)为半径,构造灰狼位置Xi(t)的邻域Ni(t):
Ni(t)={Xj(t)|Di(Xi(t),Xj(t))≤
Ri(t),Xj(t)∈Pop},
(19)
其中,Di为Xi(t)到Xj(t)的欧氏距离。其次通过多重邻域学习法,由邻域内随机d维灰狼位置Xn,d(t)和狼群矩阵内随机灰狼位置Xr,d(t)计算d维候补位置Xi-DLH,d(t+1):
Xi-DLH,d(t+1)=Xi,d(t)+rand×(Xn,d(t)-Xr,d(t)).
(20)
3)选择和更新阶段。比较Xi-GWO(t+1)和Xi-DLH(t+1)的适应度值来选择较优的候选位置:
(21)
更新搜索灰狼位置Xi(t+1)后,若所得Xi(t+1)的适应度小于原位置Xi(t)的适应度,则由Xi(t+1)更新位置Xi(t)。否则,原位置Xi(t)保持不变。对所有个体进行迭代搜索,直到最大迭代次数结束。
在GWO中α、β、δ引导狼群进入搜索空间中,找到最优解的区域,但容易陷入局部最优解。而在I-GWO中,每次迭代既有由DLH生成的候选狼,也有GWO搜索策略生成的候选狼,为了使狼从当前位置Xi移动到更好的位置,在每次迭代中选择上述两种候选狼中较优的,来更新当前位置,从而解决GWO算法陷入局部最优解的问题。
2 构建预测模型
将采集的炮控箱信号利用灰色关联度分析进行处理,把影响炮控箱状态的信号参数进行排序,剔除掉关联度小的引脚信号,分析不同引脚信号对炮控箱的影响,由筛选的信号参数对炮控箱的状态进行分类,根据关联度大的引脚以及炮控箱的状态类别来构建预测所需的样本数据集。数据集的最后一列为炮控箱的状态模式列,将炮控箱数据集划分为训练样本和测试样本。
对笔者预测所用的工具支持向量机进行优化,优化的参数为惩罚因子C与核参数g,笔者对支持向量机的优化是利用基于DLH搜索策略改进的灰狼算法。相较于传统的GWO算法,笔者提出的基于DLH搜索策略改进的灰狼算法,通过增加狼群搜猎方式多样性的方法,来解决传统的GWO算法中易收敛、陷入局部最优解等难题。
利用输出的最优参数提高支持向量机的性能,在构建好优化的支持向量机后,将训练样本和测试样本输入支持向量机,对测试样本进行预测,将预测结果与实际测试样本进行对比,即可得出预测结果的准确率。
基于DLH搜索策略改进的灰狼算法优化支持向量机的流程图如图2所示。
3 实验验证
笔者选用某型坦克火控系统中的炮控箱部件作为研究对象。通过装备试验台采集了炮控箱组设备中32个引脚信号的数据值,将采集的正常状态下数据值的平均值作为参考序列,原始数据值作为比较序列,对处理过的数据进行灰色关联度分析,求出各个引脚之间的关联度,部分引脚顺序排列关联度如表1所示。

表1 部分引脚灰色关联度
其中部分引脚的具体输出信号为固定值,虽然有小幅度的上下浮动,但可通过数值直接判断炮控箱相应模块的状态。在剔除这类引脚之后选取关联度在0.9以上的引脚信号,构建了以13个引脚信号作为特征信号的样本数据集。通过分析这13个引脚信号对炮控箱的影响之后,可以将炮控箱状态分为5种模式标签,这5种模式标签如表2所示。

表2 炮控箱数据集标签
将选取的13个引脚信号和炮控箱状态模式构成数据集的数据标签。选取300组炮控箱数据进行实验验证,为了提高实验结果的可靠性,进行3组实验对比分析:实验1中对每一类状态模式中一半的数据组进行抽取,将抽取的150组数据作为训练样本,剩余150组数据作为测试样本;实验2中对每一类状态模式中的数据抽取40组,将抽取的200组数据作为训练样本,剩余100组数据作为测试样本;实验3中对每一类状态模式中的数据抽取20组,将抽取的100组数据作为训练样本,剩余200组数据作为测试样本。
将样本数据集送入GA-SVM、GWO-SVM、IGWO-SVM、BP神经网络中,训练样本进行预测。其中设定GA-SVM、GWO-SVM和IGWO-SVM中的种群数量为20,迭代次数都取100次,BP神经网络中隐含层节点为10。以实验1中的预测结果为例,其预测结果如图3所示。
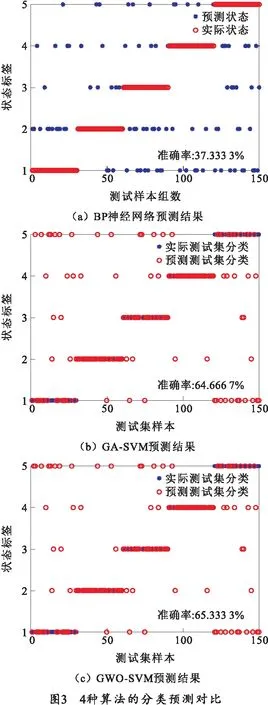
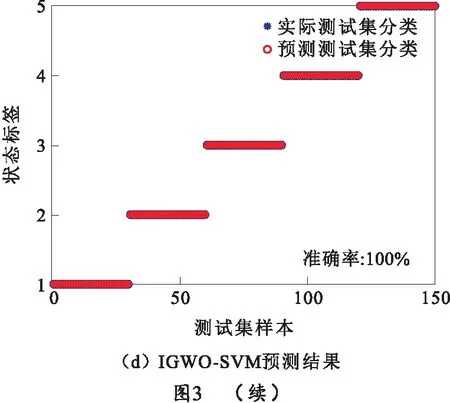
为了增加实验结果的说服力,笔者在进行实验1、2、3时,分别对每种算法进行了10次状态预测实验,其预测结果对比分析如表3所示,表中数据为10次状态的平均值。通过对3种不同组数的训练集和测试集的实验对比分析发现,在4种算法的状态预测对比中,BP神经网络预测平均所用时间最短,GWO-SVM处理用时次之,随着训练集组数的增加IGWO-SVM处理平均用时与GA-SVM处理平均用时接近;BP神经网络预测结果非常不稳定,GA-SVM的预测结果也不太稳定,GWO-SVM和IGWO-SVM预测结果比较稳定,且训练集组数越多对结果预测越准确,但是IGWO-SVM在状态预测准确率方面明显优于另外3种算法,预测结果的精度对训练集组数的依赖性也小于其他3种算法。

表3 实验1~3中4种算法的对比分析
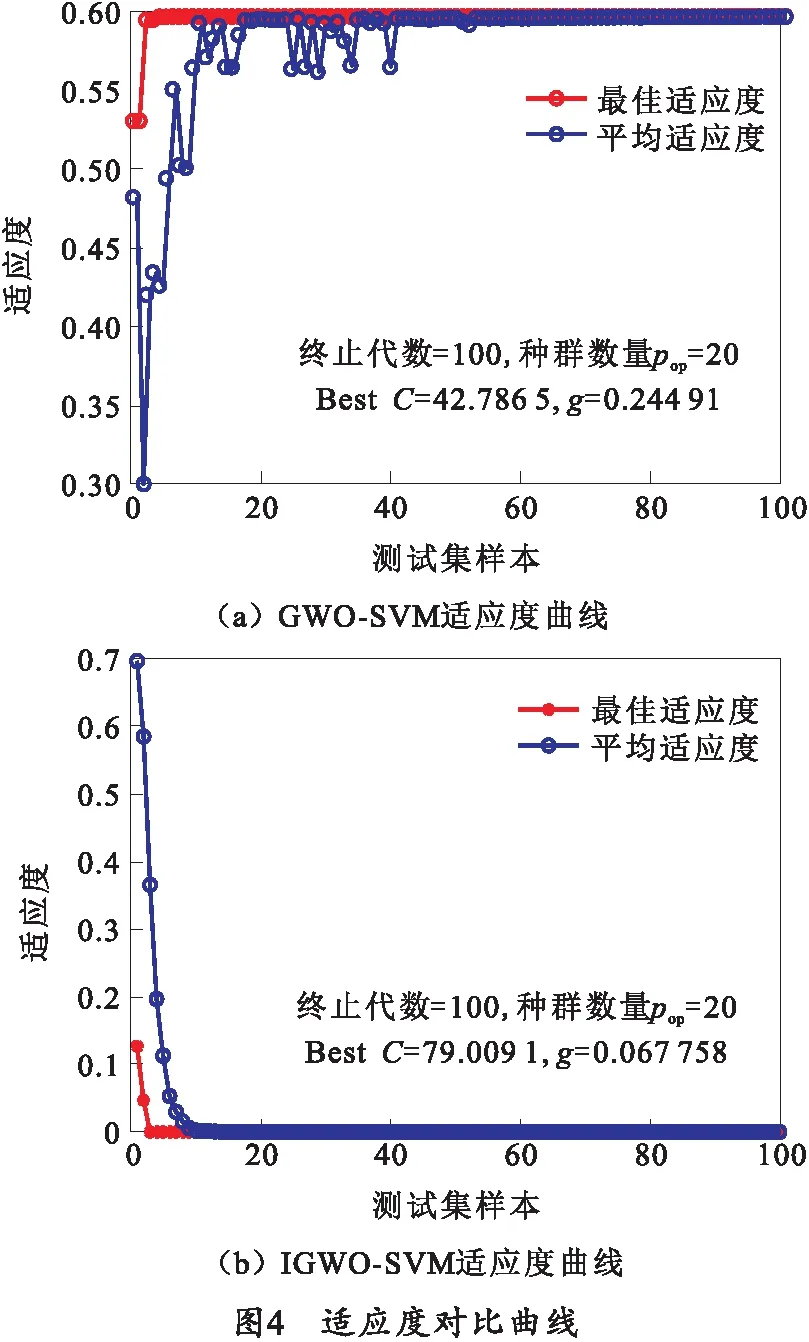
以实验1中改进灰狼搜索策略算法适应度与灰狼搜索算法适应度的曲线为例,对比结果如图4所示。
从适应度曲线对比可以看出IGWO-SVM寻找到最优适应度所用迭代次数明显少于GWO-SVM,同时IGWO-SVM计算出的适应度值也明显优于GWO-SVM计算的适应度值,这意味着IGWO-SVM可以更快更好地找到适应度最好的个体,提高了支持向量机的预测准确性,具有明显的优越性。
4 结束语
笔者提出灰色关联度分析方法对火控系统采集的信号进行约简处理,将约简后数据构建的训练集和测试集作为支持向量机的输入,采用改进灰狼搜索策略算法优化支持向量机,应用于对炮控箱组获取的数据进行状态预测。采用灰色关联度分析对数据进行处理,筛选出依赖程度高的数据组作为支持向量机的输入,降低了输入模块的维数,简化了网络结构。相比于BP神经网络、GA-SVM、GWO-SVM这3种故障预测方法,IGWO-SVM对炮控箱的状态进行预测的效果更好。
