基于麻雀搜索算法优化BP神经网络的深远海养殖平台系缆力预报研究
2022-12-29许条建金延儒蒋梅荣麻常雷
许条建,金延儒,4,蒋梅荣,麻常雷
(1 大连理工大学,海岸和近海工程国家重点实验室,辽宁 大连 116024;2 中海油研究总院有限责任公司,北京 100028;3 国家海洋技术中心,天津 300112;4 中交四航工程研究院,广东 广州 510230)
近年来,水产养殖由近海逐步走向深远海。相较于近海养殖,深远海养殖拥有开阔的养殖环境,有利于降低鱼病的发生概率,提高养殖水产品品质。深远海养殖平台作为深远海养殖的重要生产设施,也是中国先进装备制造的体现[1]。然而,深远海养殖平台要面临更加恶劣的海洋环境。深远海养殖平台的系泊系统是对抗台风等极端海洋环境荷载的最重要的基础,如果系泊系统遭到破坏,意味着整个平台失效,对养殖户而言是一场巨大的灾难[2]。因此,极端恶劣海况下深远海养殖平台的系缆力的高效、快速预报,是实现中国深远海养殖产业健康发展的必然选择。
关于深远海养殖平台的水动力特性研究方面,许条建[3]采用集中质量法和刚体运动学原理,对组合式网箱及其系泊系统在波浪、海流作用下的水动力特性开展了研究,其数值模型是开展本研究的重要基础。Li 等[4]研究了不规则波浪下深远海船型浮式养殖平台的运动响应。李玉成等[5]分析了深远海养殖平台中网衣在不同变形状态下水阻力系数。唐鸣夫等[6]分析了不同养殖密度下养殖网箱周围的流场变化以及网衣的变形。
近年来,基于人工智能的深度学习方法已经在海洋工程动力响应和安全评估方面得到了广泛应用。陈海等[7]利用人工神经网络监测半潜式平台模型在风、浪、流联合作用下的运动响应。漆徐良[8]通过人工神经网络完成FPSO系缆力的实时预测分析,对各类海况下FPSO的系缆力和运动响应进行实时监测。陈磊[9]使用BP神经网络(Error Back Propagtion)对海洋平台桩基的轴向承载力进行分析和预报。刘浩然[10]使用BP神经网络对深远海钛合金结构进行健康诊断。夏天亮等[11]引入BAS-BP神经网络对南海北部海域的波浪要素进行预报。王维[12]将机器学习应用于海底管道的损伤识别监测研究。李志鑫等[13]使用机器学习实现适用于各种水文条件下孤立波振幅的分析。周世博等[14]采用机器学习进行海洋平台受坠物碰撞的损伤分析。张鹏辉[15]和李海涛等[16]均针对船舶与海洋工程常见的材料腐蚀速率采用机器学习进行预测分析。高明星等[17]针对FPSO舷侧结构的耐装性能使用机器学习进行优化设计。虽然BP神经网络等机器学习方法已经可以完成监测和预报工作,但是人们始终还在追求预报精准度和效率的道路上不断探索。
本研究引入麻雀搜索算法,对BP神经网络的权值和阈值进行优化调整,改善BP神经网络自身容易收敛到局部最小点的缺陷,提高深远海养殖平台系缆力快速预报模型的性能。
1 深远海养殖平台预报模型分析方法
1.1 养殖平台动力响应数值模型
深远海养殖平台主要包含浮架、网衣和锚绳等构件。其中,浮架为刚性构件,采用刚体动力学建立其运动微分方程[18];对于网衣和锚绳这类柔性构件,采用集中质量法,将集中质量点作为节点、无重量的弹簧作为单元来模拟网衣[19-20]和锚绳[21-23],分别建立其运动微分方程;最后采用四阶Runge-Kutta 法联立求解深远海养殖平台及其系泊系统的运动微分方程。
无论刚性构件还是柔性构件,运动微分方程都要基于牛顿第二定律进行建立,将结构运动与荷载联系起来。对于深远海养殖平台,重力、浮力和水动力(包括波浪力和流荷载等)等荷载是深远海养殖平台主要考虑的荷载类型。其中,对于波浪力,由于结构杆件都为圆管形式,直径均远小于波长,故选用Brebbia和Walker[24]提出的修正的Morison方程来计算波浪力:
(1)
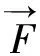
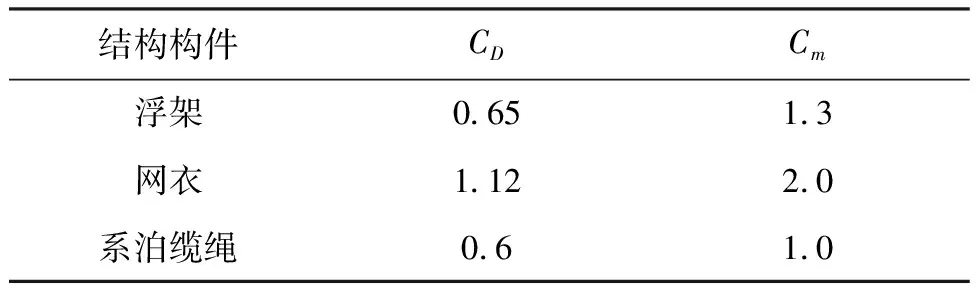
表1 深远海养殖平台各构件水动力系数
对于流荷载使用如下公式:
(2)
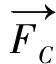
通过数值模型的建立和求解,获得各种工况下的系缆力,并建立样本集,进行后续预报模型的构建。
1.2 BP神经网络
BP神经网络由输入层、隐藏层和输出层构成,层与层之间全连接,同一层之间的神经元无连接。如图1所示,在BP网络中,数据经归一化处理后,从输入层开始,经隐藏层之后逐层向后传播至输出层;训练连接权值时,会从输出层开始,经过隐藏层向前修正网络的连接权值;循环重复上述过程进行权值与输出层数据的迭代。经多次迭代达到标准后,输出的数据进行反归一化得到最终的结果[28]。
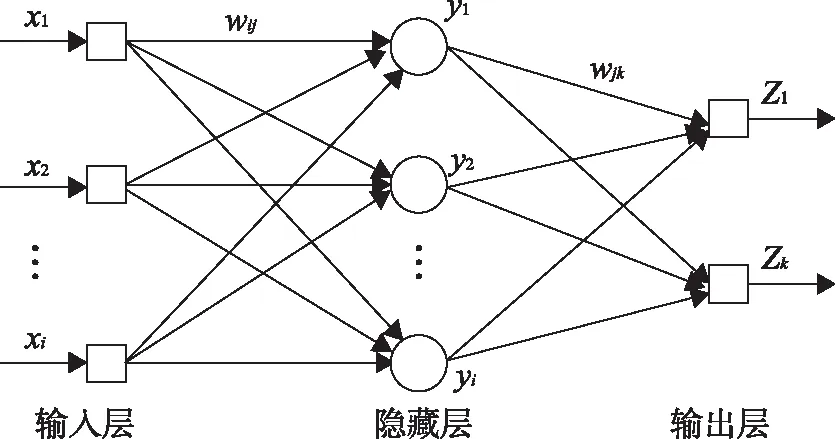
图1 BP神经网络结构图
BP神经网络算法由式(3)~式(6)确定。
yj=f(Xj+bj)
(3)
Zk=f(Yk+bj)
(4)
(5)
(6)
式中:训练数据中x作为输入,z作为输出,输入神经元个数为I,隐藏神经元个数为J,输出神经元个数为K的一个三层前馈神经网络。其中y为隐藏层,隐藏层第j个神经元的阈值用bj表示,输出层第k个神经元的阈值用bk表示,输入层第i个神经元与隐藏层第j个神经元之间的连接权值用wij表示,隐藏层第j个神经元与隐藏层第k个神经元之间的连接权值用wjk表示,隐藏层的输入用Xj表示,输出层的输入用Yk表示。f为转换函数,隐藏层的计算结果为yj,输出层输出结果为Zk。
在BP神经网络中,如果神经网络输出结果zk与训练数据的输出zk差别过大,会进行误差的反向传递,采用梯度下降法将误差按权重逐层分配并迭代计算连接权值。
然而,BP神经网络的问题也很明显,其中最为关注的是受权值和阈值影响误差而产生的局部极小问题。因为梯度下降法是沿着负梯度方向寻找最优解,当误差与权值和阈值相关的函数找到梯度为0的点,则已经达到局部最小点,权值的迭代将停止。如果该网络的误差函数具有多个局部最小点,则不能保证最终确定的权值为最优的[29]。因此,需要对权值和阈值进行优化调整,并观察误差情况。
1.3 麻雀搜索算法
麻雀搜索算法(Sparrow Search Algorithm,后面简称SSA)是Xue等[30]受到麻雀觅食以及反捕食行为所提出来的,该算法依据麻雀捕食的仿生学原理提出来的。SSA算法中,麻雀种群包含发现者、加入者和侦察者。发现者由于适应度较高,可引导并提供给加入者觅食区域和方向;加入者为了获取更好的食物,会一直跟随发现者,并监视发现者,为保证捕食率甚至会争夺食物;当侦察者发现捕食者后立即发出警报,麻雀种群集体做出反捕食行为。
发现者的位置更新如下:
(7)
式中:t表示当前迭代次数;T表示最大迭代次数;xi,j(t)表示第i只麻雀在第j维迭代次数为t时的位置信息值;α为[0,1]的随机数;r2(r2∈[0,1])表示预警值;ST(ST∈[0.5,1])表示安全值;Q为服从正态分布的随机数;L表示一个1×d的矩阵,其中内部每个元素都为1。
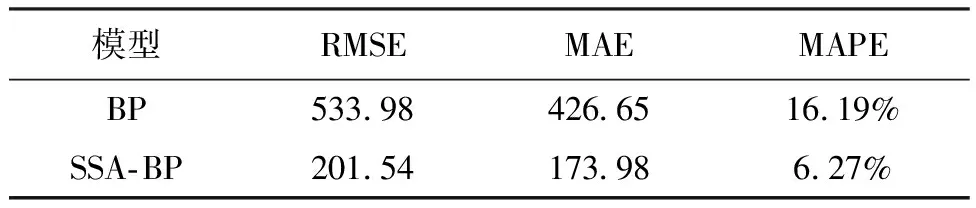
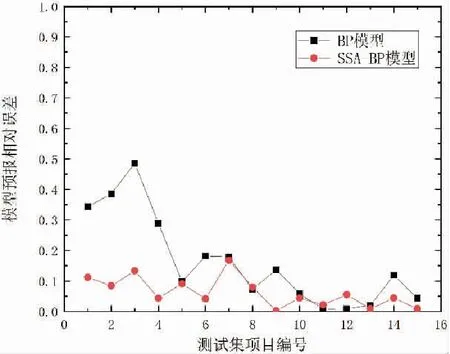
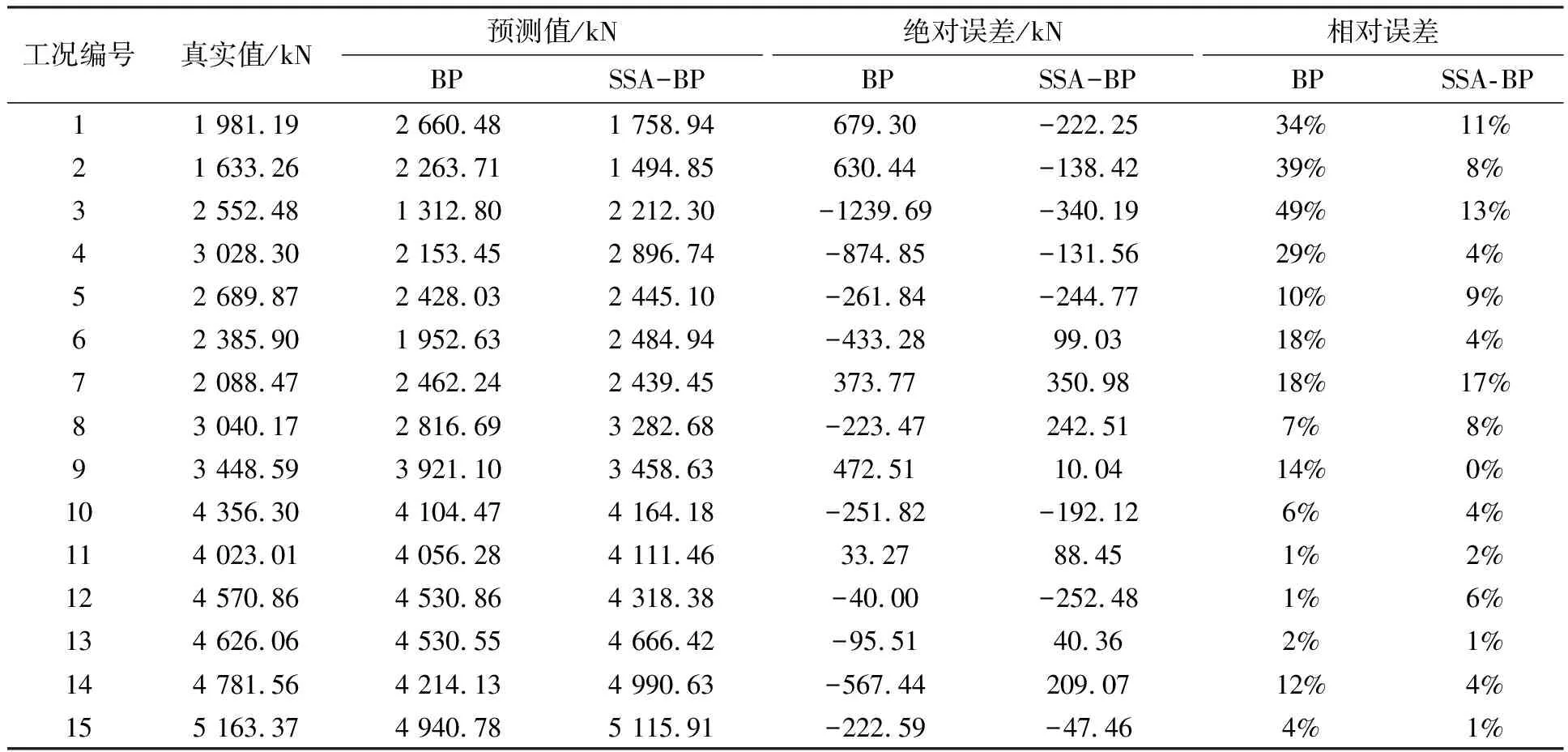
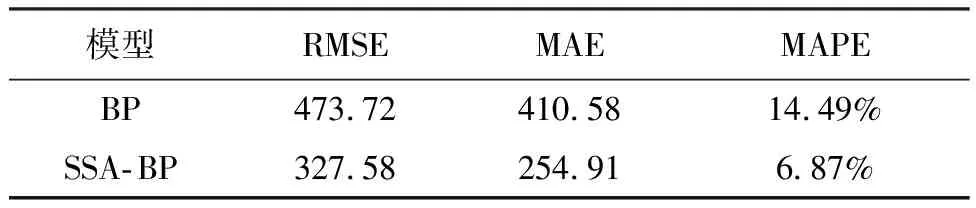
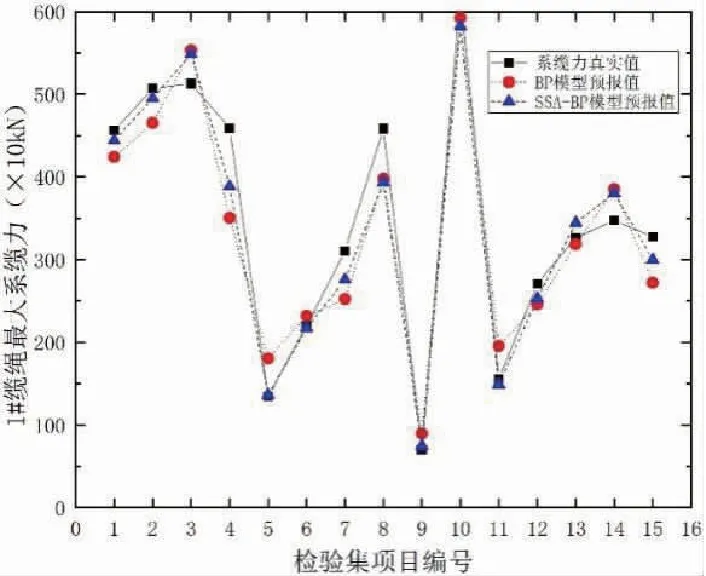
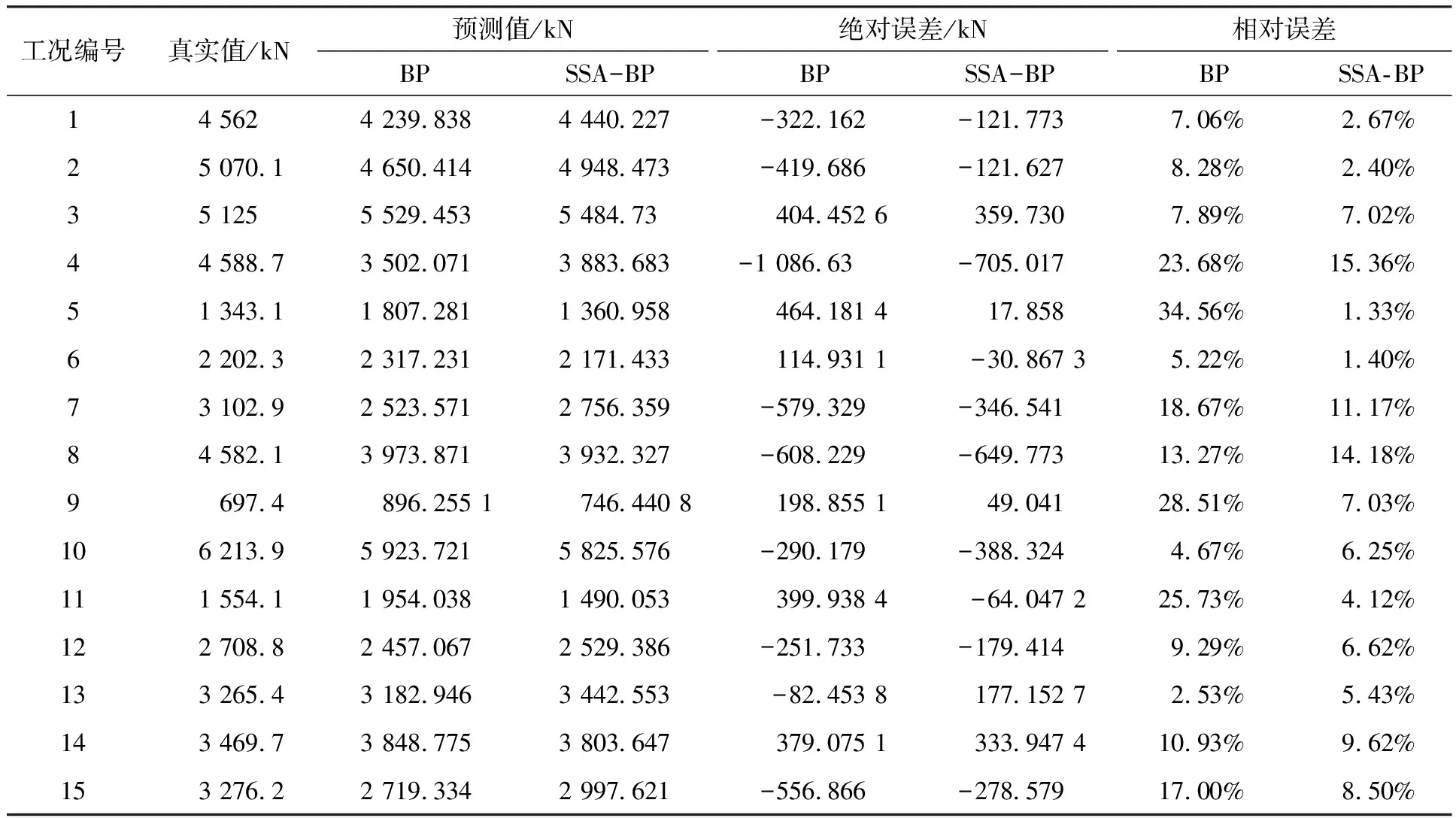
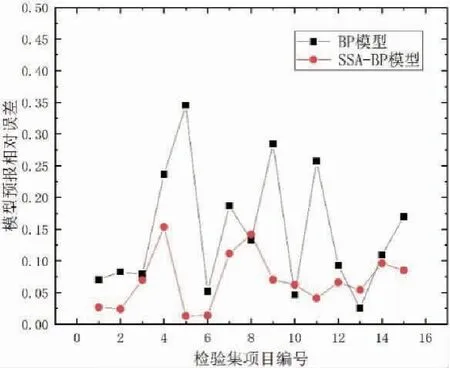
当R2 加入者的位置更新如下: (8) 式中:xworst(t)表示当前全局最差位置;xij(t)表示发现者占据的最佳位置;A+=AT(AAT)-1,A表示一个内部元素随机分配1或-1的1×d矩阵,AT为A的转置。 当i>n/2时,表示适应度值较差的第i只加入者处于饥饿状态,它需要飞往其他方向寻找食物。侦察者一般占种群的10%到20%,位置更新公式如下: (9) 式中:xbestj(t)表示当前全局最佳位置;β为服从均值为0、方差为1的正态分布随机数的步长控制参数;K∈[-1,1]表示麻雀运动方向,也是步长控制参数;fi表示当前麻雀的适应度值;fg和fw,分别表示当前全局最优值和最差值;e为一个常数,是为了避免分母为0。 当fi>fg时,表示麻雀处于种群的边缘地段,易受到捕食者攻击,当fi=fg时,表示处于种群中间位置的麻雀意识到危险,因此需要靠近其他麻雀来减少被捕食的概率。 基于麻雀搜索算法改进的神经网络算法(后面简称SSA-BP模型)对深远海养殖平台系缆力预报模型的具体建立过程如下: 步骤1:首先将数值模型的计算结果整合成样本集﹐同时按照训练集∶测试集=5∶1的比例随机划分为两组数据﹐之后对训练集全体数据以及测试集的输入指标数据进行归一化处理。 步骤2:完成BP神经网络初始化,包括隐含层层数、隐含层的节点个数、层与层之间的传递函数等。 步骤3:输出BP神经网络预报结果,并在反归一化后依据评估指标进行后续评估。 步骤4:完成麻雀搜索算法中麻雀种群相关参数初始化。 步骤5:确定每只麻雀的初始位置。 步骤6:依据公式(7)~(9),分别更新每只麻雀的位置。 步骤7:输出最优的麻雀个体位置,并将其作为BP神经网络各层之间的权值;同时输出全局最优解,将其作为BP神经网络各层的阀值;完成BP神经网络各参数的优化。 步骤8:使用优化后的BP神经网络进行训练,并比较各项评估指标。如果满足误差指标,便可以结束计算,输出对应的结果;否则,重新从步骤4开始执行。 整个算法流程见图2。 图2 SSA-BP算法流程图 预报模型整体的评估指标主要选取平均绝对误差MAE、平均绝对百分比误差MAPE以及均方根误差RMSE作为主要,其计算公式见(10)~(12)。其中,平均绝对百分比误差MAPE是本研究重点关注的评估指标,其评估标准见表2。这3个评估指标的数值越小,模型越精确。 表2 模型预测精度评估标准 (10) (11) (12) 式中:yforecast表示系缆力的预测值,kN;ytrue表示系缆力的真实值,kN。 对于系缆力预报值的评估指标,主要是依据绝对误差、相对误差以及相关性等进行分析。 如图3所示,对该深远海养殖平台系缆力进行预报分析。 图3 深远海养殖平台及其系泊系统 该养殖平台的主尺度如表3所示,锚链参数见表4。 表3 养殖平台主尺度 表4 系泊锚链参数 以图3中1#缆绳的锚绳力预报为例。该模型共有13 525个单元,平均一个算例计算100 s需要的时间为1 d。 根据所选的深远海养殖平台的工程实际位置的水文资料,数值模拟的水深为22 m,波浪和水流的方向均为45°方向(图4)。 图4 深远海养殖平台俯视图以及波浪、海流方向 对于训练样本的构建,依据该平台所在地的水文资料选取。波高分别为5 m、6 m、7 m、8 m、9 m和10 m。周期分别为8 s、10 s和12 s。流速分别为0.2 m/s、0.4 m/s、0.6 m/s、0.8 m/s和1 m/s。将波高、周期和流速任意组合成工况计算其对应的系缆力,共90组工况。 选出15组工况作为测试集验证网络准确性,也代表已有环境要素下任意组合之后工况的准确性(测试集工况见表5)。 表5 测试集样本表 除此之外,额外计算15组在样本范围内的任意工况作为检验集,观察其工程实际应用情况(检验集工况见表6)。 表6 检验集样本表 对于BP神经网络,分别要确定训练次数、学习率、训练目标最小误差、输入层、输出层、结构层数、隐藏层等参数。本BP神经网络模型的训练次数为1 000次,学习率为0.01,训练目标最小误差为0.000 001。输入层为3个节点,输出层为1个节点。依据本计算模型实例数据库容量并不冗杂,故按照广泛应用的1个隐藏层。隐藏层节点数依据公式(13)确定范围,并通过训练神经网络之后确定。通过表7计算结果可知,隐藏层节点个数为5时的均方误差最小,故设置5个隐藏层节点。关于权函数,本研究经多次训练,将输入层到隐藏层的转换函数确定为tansig函数,将隐藏层到输出层的转换函数确定为purelin函数 表7 隐藏层节点均方误差表 (13) 式中:l是隐含层的神经元个数,m是输入层节点个数,n是输出层节点个数,α是常数,α∈[0,10]。 对于麻雀搜索算法,初始种群规模为30;最大进化代数为50;安全值ST为0.6;发现者比例PD 为0.2;负责侦查的麻雀比例SD 为0.2。 为了验证该深远海养殖平台系缆力的预测效果,对比了测试集BP模型和SSA-BP模型的计算结果。从图5中可以得知,SSA-BP模型预报系缆力更贴近系缆力真实值,仿真测试曲线与真实值曲线拟合程度也比较高。 图5 系缆力真实值与各模型预测值对比图 对于系缆力预报的模型整体分析情况可通过表8进行定量分析。首先,SSA-BP模型的MAPE为6.27%,根据表2的评估标准,其模型评价为好,而BP的评价为良好;SSA-BP模型的MAE也小于BP模型,表示其误差也更小,说明SSA-BP模型预报的更精密;比较RMSE可以得知,SSA-BP模型预报系缆力的离散程度更小,受异常值影响程度也更小。综合来看,MAPE、MAE和RMSE这三项指标表现最好的模型均指向SSA-BP模型。 表8 模型整体评估指标对比表 对比各工况下的系缆力值预测,从表9以及图6可知,SSA-BP模型预报系缆力的相对误差值全面低于BP模型。不仅如此,在SSA-BP模型的预报下,相对误差低于10%的样本数目增加71.4%。综上,通过预报模型进行预报只需2 min左右就会给出预报结果,且误差减小也反映出SSA算法解决了BP模型自身易陷入局部极小而影响预报精度的问题。 图6 各测试样本预测相对误差对比图 表9 测试集样本预测值以及误差对照表 对任意工况进行系缆力预报模型的分析,以代表实际工况下的预报效果,对比了检验集BP模型和SSA-BP模型的计算结果。从图8中可以得知,SSA-BP模型预报系缆力更贴近系缆力真实值,仿真测试曲线与真实值曲线拟合程度也比较高。 对于系缆力预报的模型整体分析情况可通过表10进行定量分析。首先,SSA-BP模型的MAPE为6.87%,根据表2的评估标准,其模型评价为好,而BP的评价为良好;SSA-BP模型的MAE也小于BP模型,表示其误差也更小,说明SSA-BP模型预报的更精密;比较RMSE可以得知,SSA-BP模型预报系缆力的离散程度更小,受异常值影响程度也更小。 表10 模型整体评估指标对比表 图7 系缆力真实值与各模型预测值对比图 综合来看,MAPE、MAE和RMSE这三项指标表现最好的模型均指向SSA-BP模型。且与测试集相比,MAPE相差不大,意味着对于该深远海养殖平台而言,不用局限于样本已有工况,对于模型范围内的任意工况均适用。 对比各工况下的系缆力值预测,从图8以及表11可知,SSA-BP模型预报系缆力的相对误差值全面低于BP模型。其中,5号工况系缆力预报值相对误差由BP模型的34.56%经SSA算法优化后下降到1.33%。 表11 检验集样本预测值以及误差对照表 图8 各测试样本预测相对误差对比图 综上均可以看出,将BP模型的权值和阈值经过SSA算法优化后,误差大幅度降低,解决了其自身陷入局部极小而影响预报精度。整个过程获取结果相较数模较快,只需2 min左右便可快速获得较为精确的结果。 深远海养殖平台的系缆力预报模型整体评价为好,相较于传统数模计算速度快,对样本范围内任意工况均适用,能够对深远海养殖平台的系缆力预报有较好的实用性和准确性。通过使用SSA-BP模型,解决BP神经网络权值和阈值的优化,提高模型精准度。后续可以通过增加样本、改变权函数以及算法等来更加精确地进行预报,也可以研究更多荷载作用下深远海养殖平台的运动响应和结构强度、缆绳疲劳等实时预报等内容,为将来针对深远海养殖平台的预报与监测等研究和应用提供了新的思路和途径。 □1.4 算法流程
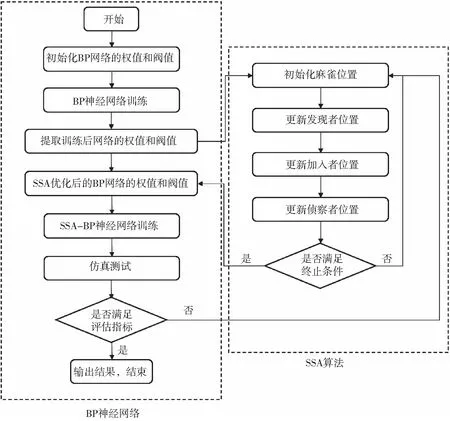
1.5 评估指标

2 深远海养殖平台系泊缆力快速预报实例分析
2.1 深远海养殖平台模型
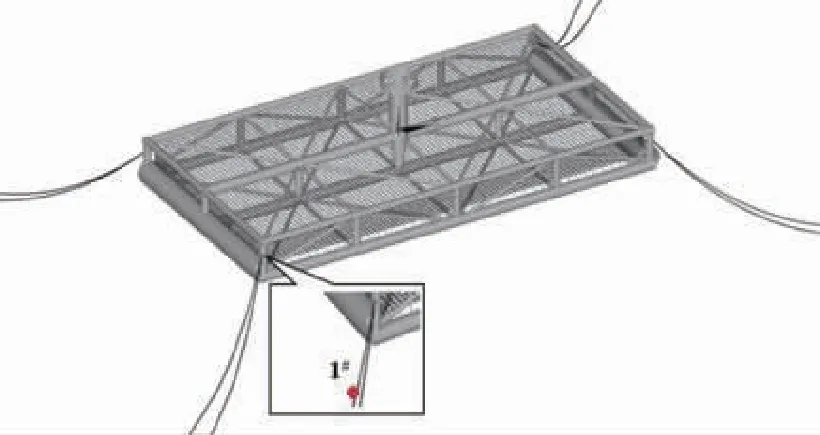

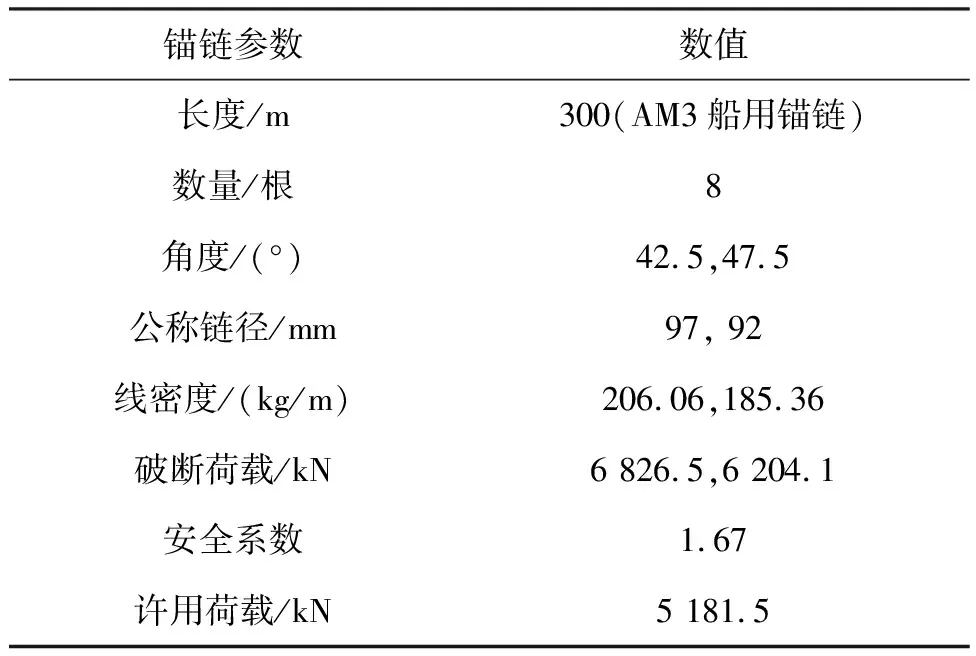
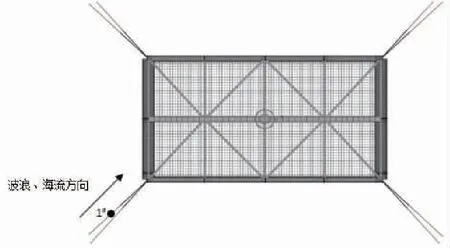
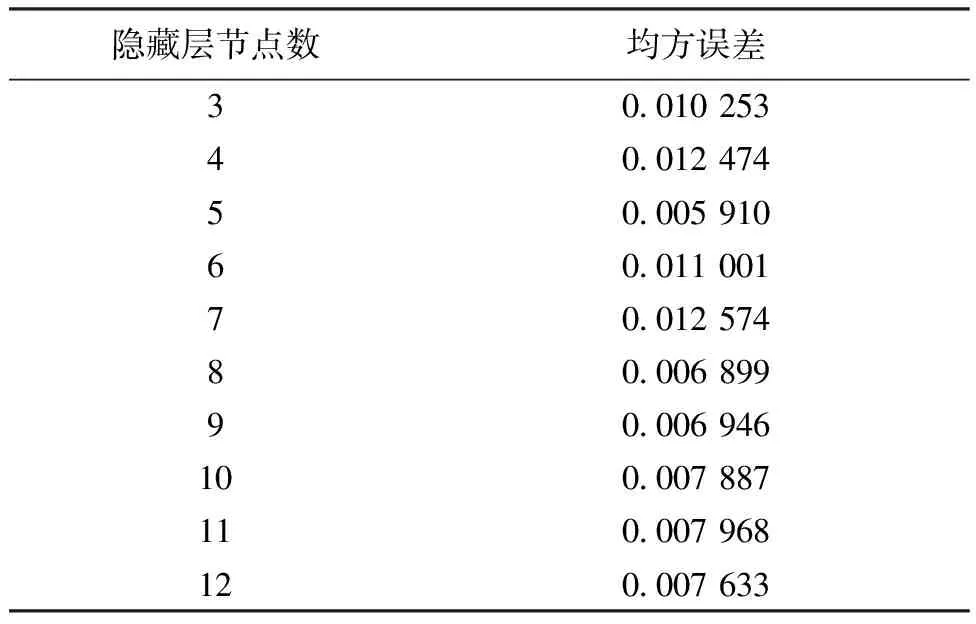
2.2 预报模型参数选定
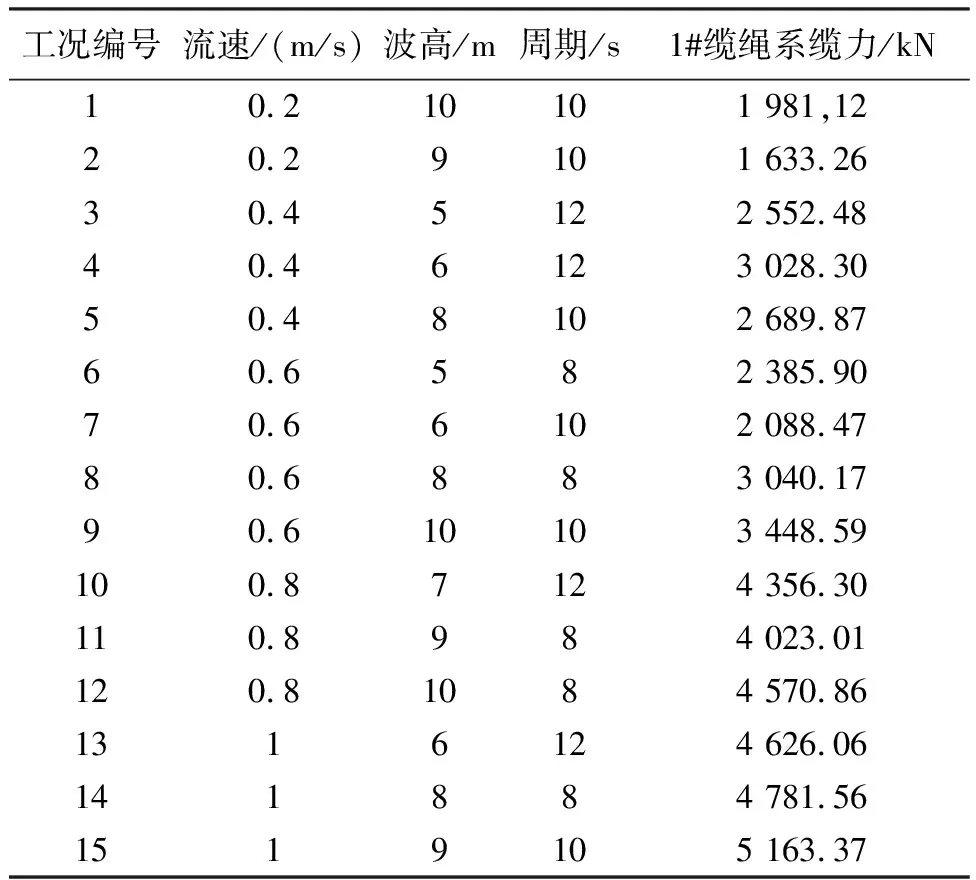
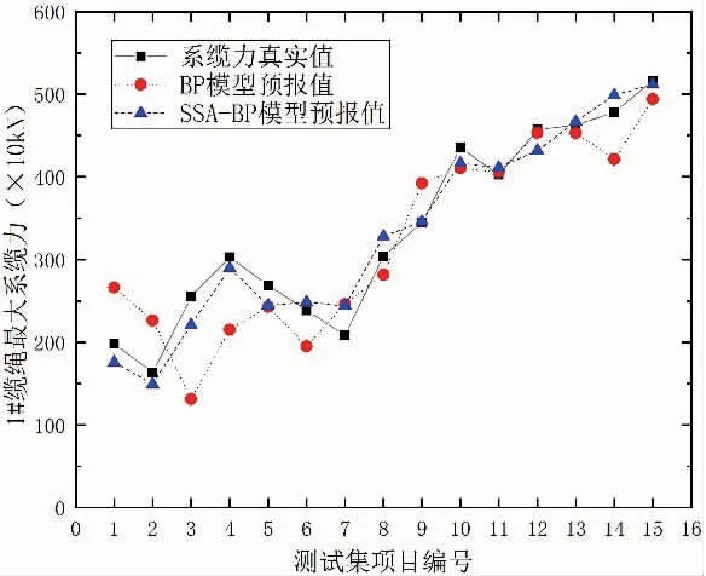
2.3 测试集结果分析
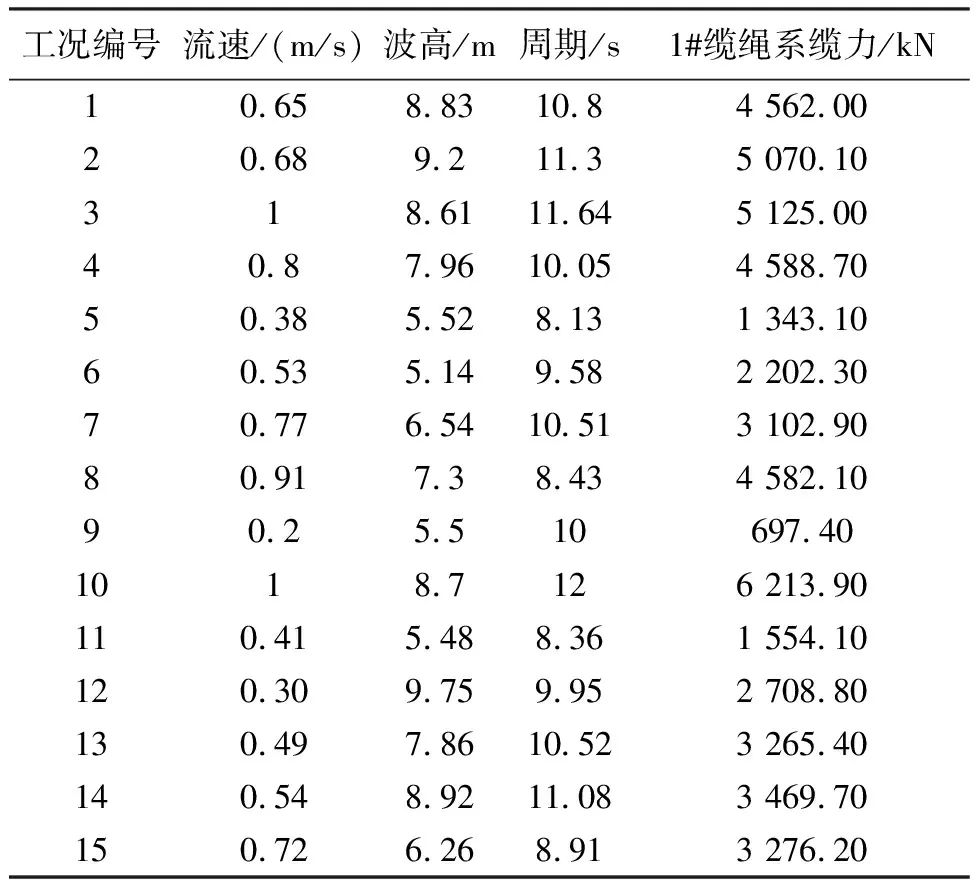
2.4 检验集结果分析
3 总结
