通用航空飞行器的参数化建模与多目标设计优化

2022-12-29徐小平张天天

航空兵器 2022年6期

徐小平，张天天，沈洋

(1.国防科技大学北京学科交叉中心，北京 100101；2.航天工程大学宇航科学与技术系，北京 101400；3.国防科技大学空天科学学院，长沙 410073)

0 引言

通用航空飞行器(Common Aero Vehicle，CAV)是一种采用通用导航、制导与控制系统以及通用空气动力学头罩的机动再入飞行器，能够装载各种类型的战斗部、传感器或情报、监视和侦察系统，并且能与多种发射系统匹配[1]。由CAV衍生出的高超声速技术飞行器(Hypersonic Technology Vehicle, HTV)项目开展了多次飞行试验，具有广阔的发展前景[2]。早期，波音公司提出的基于双锥构型的先进机动再入飞行器(Advanced Maneuvering Reentry Vehicle，AMaRV)是一种能够直接用于发展CAV项目的飞行演示系统。同时，洛克希德·马丁公司也发展了两个与CAV直接相关的项目，其中高性能机动再入飞行器(High Performance Maneuvering Reentry Vehicle，HPMaRV)系统具有详细的仿真和风洞试验数据。作为再入飞行器，采用双锥构型的AMaRV升阻比较小，被称为低性能通用航空飞行器(Low-Performance Common Aero Vehicle，CAV-L)，而采用升力体构型的HPMaRV升阻比较大，被称为高性能通用航空飞行器(High-Performance Common Aero Vehicle，CAV-H)。尽管如此，CAV-H构型的尖前缘在带来大升阻比的同时，也对防热系统提出巨大挑战。使CAV在高超声速再入环境下具有良好的空气动力学性能且不被烧蚀成为一项重要课题[3]。

无论是升阻比还是加热环境均与CAV的构型密切相关，通过构型的设计和优化有望在任务要求和材料受热极限的约束下发现可行方案。而对CAV构型的优化设计需要具备高保真度的参数化建模方法、性能评估方法和数值优化方法。其中，参数化建模方法使设计者能够将复杂的三维外形用简单的数学参数进行表示，实现对外形的精细控制[4-5]；性能评估方法能够在已知构型的基础上通过计算或者实验获得目标特性，如升阻比、容积率、热流峰值等；数值优化方法能够通过寻优，找到使目标特性最符合预期的输入参数设置。

气动外形的设计与优化一直是飞行器设计领域的热点，大量的新式翼型、飞行器构型在优化中产生，使飞行器设计水平显著提高。其中，三维类别/形状转换(Class/Shape Function Transformation，CST)建模[6]、三维B样条[7-8]和自由网格变形方法(Free-Form Deformation，FFD)[9]作为应用最为广泛的参数化建模方法在气动优化过程中得到广泛应用。Chen等[10]在跨声速机翼的流固耦合稳定性优化中采用CST参数化建模方法。Xia等[11]采用FFD参数化建模方法，结合改进的粒子群优化算法和径向基函数对二维翼型和运载火箭进行气动外形优化。李治宇等[12]将构型参数化、网格自动化及流场快速求解程序进行有机结合，发展了快速有效的气动布局优化设计方法, 并设计了新型高升阻比融合升力体气动布局。

考虑到单纯提高升阻比可能会给飞行器的结构、容积和防热等性能带来新的问题，在气动优化过程中往往还要同时考虑其他设计目标或约束。Zhang等[13]采用多目标设计优化的方法研究了高超声速滑翔飞行器升阻比与容积率之间的关系，发现两者难以同时达到最优。Deng等[14]在进行带翼高超声速飞行器的升阻比优化时，考虑了飞行器的容积率和操稳特性等条件带来的约束。张龙龙等[15]基于CST参数化建模方法对翼身融合升力体构型进行参数化设计和多目标优化。Zuhal等[16]基于代理模型对翼型进行多目标气动外形优化，比较了不同加点方法对优化效率提升的影响。

尽管气动优化理论已经得到广泛关注和蓬勃发展，然而类似CAV这样的三维曲面构型，其参数化建模的精度与参数数量之间的矛盾依然存在，高超声速条件下其升阻比与热流峰值之间的矛盾仍然难以调和，优化设计精度和效率还需进一步提升。本文提出了针对不同类型CAV构型需灵活选择三维参数化方法的理念，为CAV的高效参数化建模提供参考；通过多目标设计优化，获得以CAV构型升阻比、容积率和峰值热流为目标的三维非劣解前缘，并对其进行深入分析，提高了CAV构型设计水平。

1 CAV构型参数化建模方法

1.1 传统参数建模

已知CAV-L为双锥构型，其长度处于107～144 in之间，尾部直径为36 in。此类旋转体构型只需对二维轮廓进行参数化设计，并结合双锥构型的特点，即可实现用少量参数实现三维构型的参数化建模，如图1所示。

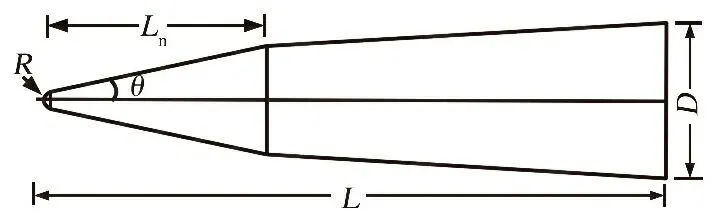
图1 CAV-L构型设计参数示意图

可见，对于此类简单的双锥构型，只需5个参数即可确定其旋转体外形，分别为头部钝化半径R，一级头锥角度θ，一级头锥长度Ln，总长度L和尾部直径D，其他特征参数如二级圆台长度、锥角等均可由上述参数的确定而得到。由于尾部直径D给定，钝化半径可根据防热需求另行确定且对构型整体形状和性能影响较小，因此，该构型的实际有效控制变量分别为L，Ln和θ。依据公开资料，设定L=144 in，Ln=50 in，θ=12°。

同时，给定钝化半径R=2 in，则可得CAV-L的三维构型。波音公司设计的实验构型是在旋转体构型的基础上通过安装气动控制舵面以及稳定装置来满足飞行需求。本节则通过削平底面并切割的方式得到控制舵，并在构型两侧对称安装固定控制面，得到的三维概念构型如图2所示。该构型与公开资料中的CAV-L构型高度相似。

图2 CAV-L构型3D模型概念图

1.2 三维CST曲面参数化建模方法

CAV-H为升力体构型，虽然具有面对称的特点，但其上下表面均为曲面，难以用传统的参数化方法进行表示，因此，需要采用新型三维曲面参数化方法进行建模，并为构型优化打下基础。

类别/形状转换(CST)参数化方法是一种两层曲线参数化方法。该方法的出发点是建立一个具有目标曲线基础形状的类函数，然后建立一个形状函数对类函数进行进一步修饰。CST方法的表达式为

(1)

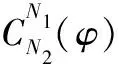
在二维CST方法的基础上，首先建立横、纵坐标之间的CST函数关系，然后引入第三维坐标，建立其与横、纵坐标之间的三维关系，从而能够对三维曲面进行参数化建模。三维参数化方法的表达式为

(2)

ΔεM, N(φ,η)

(3)

式(3)建立了Z方向坐标与X和Y方向坐标之间的关系，其中X方向坐标归一化后用φ表示，Y方向坐标归一化后用η表示，两者的类函数和形状函数组合构成了曲面表达式；nx和ny分别为两个Bernstein方程的阶数。由类函数和形状函数表达式可知，在X和Y分别取极值时类函数和形状函数均等于0，即曲面边线均处于Z=0的平面上，为此，三维方程引入ΔεM,N(φ,η)来定义曲面边缘所处的空间位置。ΔεM,N(φ,η)定义了曲面边缘在X-Z平面和Y-Z平面上投影的形状，具有多种形式，仍然可以采用标准二维CST方法表示，即

(4)

用该三维CST方法设计的类CAV-H构型如图3所示。该方法的详细介绍可参见文献[13]。

图3 采用三维CST参数化方法设计的CAV-H构型

1.3 FFD自由网格变形参数化建模方法

FFD自由网格变形方法通过Bernstein函数，将构型表面所有点的空间坐标映射到控制网格的节点坐标，从而实现目标的参数化。Bernstein函数在[0，1]空间内的分布如图4所示，其中黑色虚线代表各项和的分布，为一条恒等于1的直线，即Bernstein系数均取1时所有输入点得到的输出均为1；此外，当各项系数均取对应项编号与阶数的比值(例如第i项系数取i/l，l为Bernstein函数的阶数)时，其所得输出等于输入值，如图4中的红色斜线所示。通过调整各系数的取值，即可对应调整函数输出，若将归一化的控制网格节点坐标直接作为Bernstein系数，则当其均匀分布时，构型形状不变，而当控制节点坐标改变时，则会对应改变Bernstein系数，从而改变构型形状。

图4 Bernstein函数各项及其组合项在[0, 1]空间的分布

综上所述，可引出FFD方法中控制节点坐标Qi, j, k对设计对象任一点坐标(x,y,z)的控制函数Pffd：

(5)

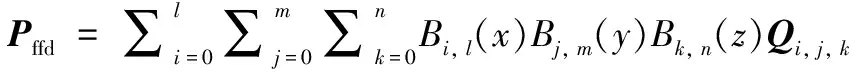
(6)

式中：i=0, 1, …,l;j=0, 1, …,m;k=0, 1, …,n;l，m，n为x，y，z三个方向上的Bernstein函数阶数，为便于计算，将控制点坐标和控制体坐标均认为是归一化后的坐标。

2 性能计算方法

2.1 高超声速气动性能工程估算方法

高超声速工程估算方法是一种快速估算构型高超声速气动性能的方法。该方法认为在高超声速条件下，物体迎风表面的压力系数Cp与表面法线和来流之间夹角正弦值的二次方正相关，计算方程如下：

Cp=Cpmaxsin2δ

(7)

式中：Cpmax为相关系数，该值可采用正激波驻点后的压力系数值。

(8)

式中：p0，p∞，ρ∞和V∞分别为自由来流的总压、静压、密度和速度。由于

(9)

且

(10)

从而得到

(11)

对于飞行器背风面则可采用Prandtl-Meyer膨胀波理论进行求解。已知当来流马赫数大于1时，经过钝角物面的来流速度增加、压力降低，形成膨胀波，Prandtl-Meyer膨胀波理论则定义了偏转角度与来流马赫数之间的函数关系，即

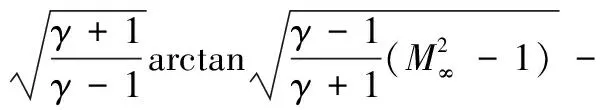
(12)

根据压力系数与流动转折角之间的关系：

(13)

则可计算得到背风面物面的压力系数。

由于飞行器为连续曲面构型，而高超声速工程估算方法反映的是局部来流迎角与当地压力系数之间的关系，因此，为计算构型整体受力，需要采用面元法将构型表面分成多个微小面元，分别计算压力系数分布后求和得到构型整体受力。

面元的划分有多种方式，最常见的是三角面元和四边形面元划分方法，如图5所示。

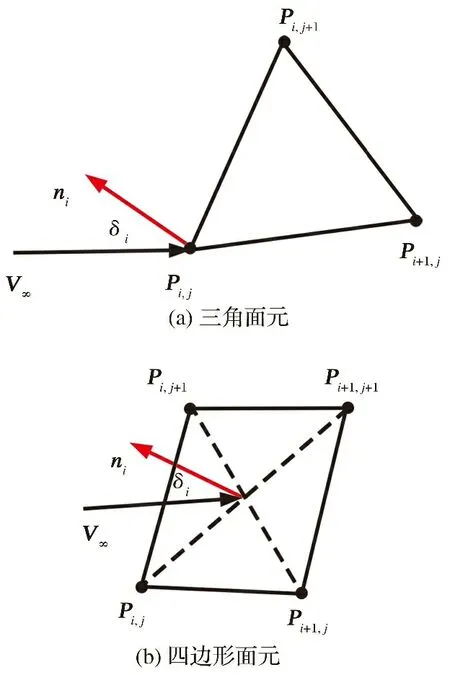
图5 两种面元划分方式及其与来流之间的关系

面元划分相当于将物体表面离散化，对每个面元的气动受力求解前需要先求出当前面元的单位法向量ni和面元面积si。面元法向量用于求解面元迎风角，面积用于计算面元所受来流压力。

对于四边形面元，面元法向量求解方式为

(14)

四边形面元的面积有多种求法，其中一种为

(15)

四边形相邻面元之间的拓扑关系相比于三角面元更加具有规律性，因此，采用四边形面元划分方法，如图6所示。

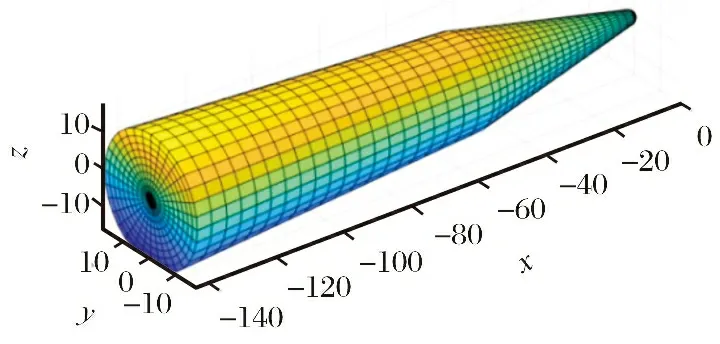
图6 CAV-L表面的四边形网格划分

2.2 容积率计算方法

容积率(ηv)是反映飞行器有效载荷装填能力的参数，定义如下：

(16)

式中：V和S分别代表飞行器的体积和表面积。容积率越大，表明同样容积的飞行器更适合用于装填有效载荷。换言之，同等表面积的飞行器，容积率越大，其内部容积也越大。例如，长方体的容积率小于同等体积的正方体，同样表面积的细长体容纳有效载荷的能力不如球体。

2.3 热流估算方法

高超声速条件下的气动加热现象不可忽略，为避免飞行器被烧蚀，需要通过构型设计使飞行器表面加热约束在材料耐受范围以内。已知飞行器的驻点处于弓形激波正后方，其气动加热现象最为显著，因此，采用工程算法估算驻点热流量qs，即

(17)

式中：Rs为驻点处的曲率半径；ρ0为海平面大气密度；C为固定常数，取值为2.146×10-4J·m-4.5·s2[17]。可见在来流条件一定的前提下，驻点曲率越大，热流量越大。

3 优化方法

3.1 基于遗传算法的单目标优化方法

遗传算法通过模拟自然界中“优胜劣汰”的生存法则来使优化问题收敛到最优结果附近。算法首先在参数设计空间内随机抽取一部分样本点，称为种群；然后计算种群内每个个体的响应结果(即适应度)，并根据适应度大小对种群进行排序，在此基础上产生下一组种群并按此过程迭代循环直到满足迭代终止条件。在此过程中用于产生下一组种群(子代)的当前种群被称为亲代；在亲代中选择优胜个体并淘汰劣势个体的过程称为选择；由优胜个体产生子代的过程称为遗传。遗传过程有三种形式：第一种是部分优胜个体(精英)直接进入子代；第二种是优胜个体间通过交换步骤将彼此的信息切断后互相再组合生成新的个体(又称交叉)；第三种则是在亲代信息基础上随机引入变异。迭代终止条件包括最大迭代代数、迭代时间、适应度函数值迭代残差值等。可见，遗传算法中的种群规模、交叉系数、变异概率和收敛条件等均会对收敛结果产生影响。

3.2 基于NSGA-II的多目标优化方法

当优化问题出现多个目标时则需要采用多目标优化算法，例如本文中不仅希望CAV构型的升阻比大，还希望其容积率大、最大热流量小。由于不同目标之间可能相互排斥，即一个目标向好的方向发展时，另外的目标反而变得更坏，此时需要引入非劣解的概念。非劣解表示不存在所有目标均优于该解的任何其他解。多目标优化的目的则是在约束范围内收敛到非劣解集。NSGA-II算法是基于遗传算法发展而来的多目标优化算法，该算法中亲代生成子代的过程仍然按照遗传算法所需的选择、交叉、变异等操作。在产生子代后要将亲代和子代的结果按照是否为非支配解进行排序，将所有当前的非劣解集筛选出记为Rank0，然后将剔除Rank0后的剩余结果再次排序，筛选出剩余解中的非劣解集并记为Rank1，以此类推。可见Rank值越小表明当前解集中解的质量越高。在标记结束后按Rank值从小到大选择子代，当达到某一Rank值时出现添加前子代数量小于预定值而添加后子代数量多于预定值，则在该Rank解集中进行拥挤度排序，并按照拥挤度从小到大的顺序补足子代所需的个体数。按照此过程循环迭代，直到满足收敛条件，最终可得到多轮迭代后的非劣解集。在该解集的基础上，设计者可以按需求任意选择可行解，所选的解尽管不能保证满足所有目标最优，但不会存在全面优于该解的其他解。

4 结果与分析

4.1 优化问题定义

根据航程公式，升阻比越大的武器打击范围也越大，因此，本文首先对CAV-L构型和CAV-H构型开展单目标优化设计，优化目标是攻角[-5°, 30°]范围内的最大高超声速升阻比。其中，CAV-L构型采用传统参数化建模方法，优化变量包括L，Ln和θ，优化问题表述为

maxL/Dmax

s.t. 107 in≤L≤144 in

15 in≤Ln≤60 in

5°≤θ≤20°

(18)

CAV-H构型采用三维CST参数化方法，优化变量包括Hl，Hu，N1u，M1u，M1l，T1u，T1l，其初始值的集合用V0表示，V0=[0.1，0.25，0.8，1，1，1.5，1]，优化过程中优化变量取值上限为1.5V0，取值下限为0.5V0，本次优化不考虑其他约束。

CAV-L和CAV-H构型的气动性能计算均在马赫数15、高度25 km的条件下，优化算法均采用遗传算法，最大迭代代数为100，每代交叉概率为0.8，变异概率为0.2，收敛精度为10-6。由于CAV-L的优化变量较少，故种群规模为40；CAV-H的优化变量较多，种群规模为50。

由于构型容积率和驻点区热流密度同样是衡量飞行器性能的重要指标，因此，进一步在CAV-L构型优化的基础上，开展以高超声速条件下升阻比最大、构型容积率最大、驻点区热流密度最小为优化目标的多目标设计优化。采用FFD参数化建模方法，以FFD控制点位置作为设计变量，将所有优化目标转化为成本型指标，产生的优化问题描述如下：

min-L/Dmax,-ηv,qs

s.t.DVmin≤DV≤DVmax

(19)

多目标优化采用NSGA-II优化算法，设置算法中的交叉概率为0.7、变异概率为0.4、种群规模为300、最大迭代次数为40次。

4.2 以升阻比为目标的单目标优化设计结果

4.2.1 CAV-L构型优化结果

CAV-L原始构型最大升阻比为2.36，处于攻角为10°的飞行条件下。

优化过程中种群最优升阻比和平均升阻比的变化曲线如图7所示，迭代100代后优化过程收敛，种群升阻比收敛到约2.69。

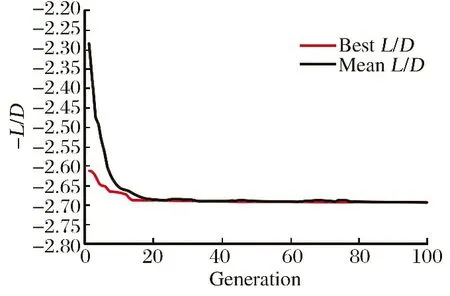
图7 CAV-L升阻比优化收敛曲线

图8所示为优化前后构型的升阻比曲线对比，优化后的最大升阻比出现在更小的攻角条件下，升阻比大小提高了12.7%。优化后的设计参数取值为L=144 in，Ln=40 in，θ=8.66°。

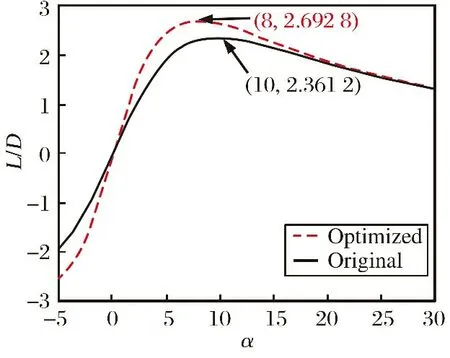
图8 CAV-L构型优化前后高超声速升阻比曲线对比

优化结果表明，总长度L的增加是造成最大升阻比增大的主要原因。该参数组合控制下的CAV-L构型如图9所示，相比于图2，优化后的构型更加细长。

图9 优化后的CAV-L构型

4.2.2 CAV-H构型优化结果

CAV-H构型的优化过程在达到最大迭代次数时停止，升阻比最优值与平均值趋于相等且收敛，升阻比最终收敛值为9.824，如图10所示。

图10 CAV-H升阻比优化收敛曲线

根据优化结果，升阻比达到最优值时的设计变量Vopt=[0.05，0.125，0.4，1.088 7，1.09，2.245，1.193 9]，前3个设计变量均趋于设计范围的最小值，第6个设计变量趋于设计范围最大值，其余3个设计变量处于最大值和最小值之间，即最大升阻比的提高主要是通过Hl，Hu，N1u的减小以及T1l的增大实现的。根据以上设计变量所得类CAV-H构型如图11所示。

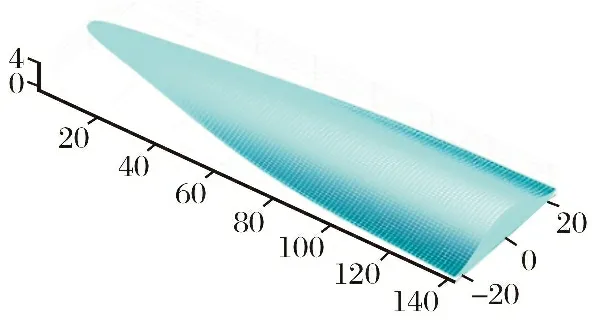
图11 优化后的CAV-H构型

图11所示的飞行器构型具有较大的升阻比，其整体呈现扁平状，相比于图3展示的参考构型，其厚度更薄，头部更宽。两者的升阻比曲线对比如图12所示。从图11～12可以看出，优化后的CAV-H构型过于扁平，很难在实际再入过程中承受气动加热，且其扁平的形状也对内部部件的安装提出巨大挑战。同时，尽管其最大升阻比较大，但随着攻角偏离最大升阻比出现的条件(2°)，其升阻比值将快速下降，使得实际飞行过程的鲁棒性较差，抗干扰能力较弱。

图12 CAV-H构型优化前后高超声速升阻比曲线对比

综上所述，仅以升阻比为构型优化目标难以得到符合工程实际需求的构型，需要采用多目标优化的方法对多个设计目标变量进行优化。

4.3 基于NSGA-II的CAV多目标优化结果

基于CAV-L单目标优化构型所构建的几何外形FFD参数化设计如图13所示，考虑几何约束设计要求的面对称性和底部平整性，在变形过程中令控制点保持xoz平面对称、底部位置的控制点在x方向上不移动。

图13 初始FFD参数化设计

多目标优化所得非劣解集(又称Pareto前缘)如图14所示。优化结果表明，相比于统计得到的Pareto前缘解集，初始外形(2.692 8，0.581 1，6.748 5)所处位置是明显的离群点，且存在较多解方案在3个指标均优于初始外形，说明算法驱动设计空间寻找到了综合性能良好的优化解集。根据Pareto前缘解集的散点分布情况来看，3个优化目标之中升阻比指标在数值上的提升较为明显，较强的负相关性存在于升阻比与容积率之间、升阻比与热流密度(效益)之间，说明在当前设计方法下，位于Pareto前缘的上述两组指标对存在着较强的矛盾。由于最大升阻比大的构型一般为细长体，而细长体构型的容积率往往会比较小，另外热流密度的减小往往需要增大构型最小曲率半径，从而增大阻力，造成3个优化目标无法同时达到最优解。

图14 CAV构型多目标优化所得Pareto前缘解集

各优化目标上的优秀外形、指标性能及FFD设计布局如图15所示。Pareto解集中的最大升阻比能够达到2.973，分析升阻比最优的外形，FFD布局直观展示了相对于初始外形的变形特征，根据FFD控制点的位移，其优化逻辑是令头部附近靠近下方的控制点前移，通过拉伸飞行器机身下前部以扩大升力面，同时令头部附近侧面控制点向内收缩，以减小外形阻力。

图15 各优化目标上的优秀外形及其FFD设计

容积率最优的外形是初始外形的支配解(即3个指标均更优)，其优化逻辑是令头部附近控制点向后收缩，减小外形较细(横截面面积较小)几何区域的表面积，从而提高体积效率；另外，令机身区域的控制点变宽，从而直接增加飞行器机身区域的体积。但上述现象与升阻比的优化逻辑显然存在矛盾。

分析针对热流密度目标的优化方式，该目标主要与局部外形特征相关。FFD结构显示其头部附近控制点形成“凹陷状”布局，使外形头部几何沿流线方向钝化，该行为与升阻比优化逻辑存在一定的冲突。但若对头部外形进行更加细致的FFD参数化设计，分别增加对驻点区与升力面的变形自由度，则有可能缓解当前优化水平的升阻比-热流密度指标对的冲突现象。

综上所述，在设计范围内，相较于初始外形，得到的Pareto解集升阻比指标中位数提升5.2%、容积率中位数提升1.4%、热流密度中位数减小6.6%，该优化过程达到了预期目的，Pareto前缘上的点可为工程中具体构型的选择提供参考依据。在后续优化中，基于FFD参数化设计，主要考虑进一步细化对外形头部变形自由度的构造，局部弱化升阻比与其他目标之间的相关性。