输入受限乘波体飞行器非脆弱预设性能神经控制
2022-12-29卜祥伟姜宝续
卜祥伟,姜宝续
(1.空军工程大学 防空反导学院,西安 710051;2.空军工程大学 研究生院,西安 710051)
0 引 言
乘波体飞行器(Waverider Vehicle, WV)飞行速度快、探测难度大、突防能力强,被认为是打破传统空天防御模式的颠覆性武器[1-4]。控制系统是WV的“神经中枢”,对于保障其安全飞行和顺利完成任务使命至关重要。控制系统的动态性能与稳态精度则是保证WV大机动飞行以及打破传统导弹突防与拦截防御模式的关键[5-6]。
预设性能控制[5-8](Prescribed Performance Control, PPC)被认为是一种能够在控制系统动态性能与稳态精度之间进行折中平衡的新理论,一经提出,便受到国际控制学界的广泛关注。鉴于PPC能够很好地保证WV大机动飞行时其控制系统所急需的动态性能与稳态精度,近年来,国内外科技人员对WV的PPC技术开展了系统而深入的研究。文献[9-10]针对传统PPC方法需要事先获取误差精确初值的苛刻条件,通过引入双曲余割函数构造了一种新型性能函数,为WV提出了一种新型PPC方法;进一步,引入神经网络对WV的未知模态进行在线逼近,保证了控制鲁棒性。针对存在不确定参数的WV,文献[11]采用反演方法设计了具有预设性能的虚拟控制律与实际控制律,并采用自适应投影算法保证了控制系统对不确定参数的鲁棒性。虽然该方法能够保证跟踪误差满意的动态性能与稳态精度,但是在线调整参数过多,算法的在线学习量有待进一步降低。文献[12]为WV提出了一种固定收敛时间PPC方法,可以定量地设置跟踪误差的收敛时间,提高了PPC方法的实用性。进一步,文献[6]将文献[12]方法改进为有限时间小超调PPC,仿真结果表明,该方法可以保证WV速度跟踪误差与高度跟踪误差任意定量的预设性能。上述PPC方法的有效性虽已得到验证,但忽略了由输入受限导致的PPC脆弱性问题。所谓脆弱性问题,是指输入受限将导致误差短时间内显著增加,当误差增加幅度足够大时,有可能导致误差过分接近甚至到达PPC的约束包络,进而导致控制奇异[5, 13-14]。考虑到WV飞行高度大,大气密度降低导致气动舵执行效率明显下降,极易造成控制执行器饱和。因此,PPC的脆弱性缺陷已经成为制约WV飞行控制研究的瓶颈难题。此外,现有基于反演设计[11-13]的WV控制策略带来了极其复杂的回馈递推设计过程,并产生一系列的中间虚拟控制律,控制复杂度还有待进一步降低。
基于以上分析,本文提出输入受限WV非脆弱PPC新方法,为WV的速度动态与高度动态分别设计具有再调整约束包络的新型非脆弱PPC,弥补现有PPC方法的脆弱性缺陷。为了保证控制鲁棒性,引入径向基神经网络(Radial Basis Function Neural Network, RBFNN)对WV归一化的未知模态进行在线逼近,并避免复杂的反演设计过程,控制复杂度得到显著降低。最后,通过数值仿真验证所提方法的效果与优势。
1 WV模型
本文采用美国NASA代号为X-43的典型WV,Bolender与Parker等学者[3-4]为其建立了在国际上被广泛采用的纵向运动模型:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
式中:V∈R>0,h∈R>0,γ∈R,θ∈R,Q∈R为刚体状态;η1∈R,η2∈R为弹性状态;Φ∈R>0,δe∈R为控制输入;κV∈R>0,κγ∈R>0,κQ∈R>0为常数;ΞV∈R,Ξγ∈R,ΞQ∈R为非线性连续可微函数[6, 15],即
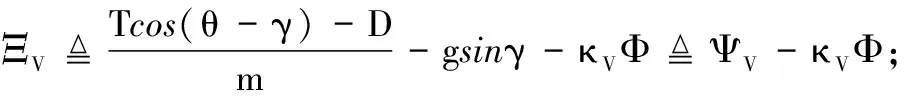

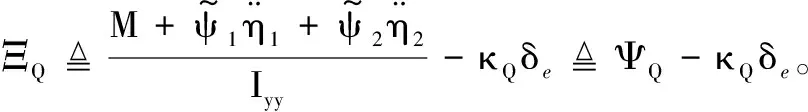
WV的几何外形与受力情况如图1所示,模型参数的详细定义如表1所示。由于WV的弹性状态无法测量,因此仅采用其5个刚体状态进行状态反馈设计,并利用控制鲁棒性对弹性状态进行被动抑制。

图1 WV几何外形与受力示意图

表1 参数定义
控制目标是:在假设ΞV,Ξγ,ΞQ为完全未知的情况下,通过为Φ,δe设计合适的受限控制律,使得速度V和高度h稳定跟踪其参考指令Vd∈R>0,hd∈R>0,并且跟踪误差满足期望的预设性能。这里,Vd∈R>0和hd∈R>0及其一阶导数均有界。
2 控制器设计
为了便于控制器设计,通常将WV的运动模型在形式上分解为速度子系统(即式(1))与高度子系统(即式(2)~(5))[9-12]。然后,分别为两个子系统设计基于神经逼近的非脆弱PPC。
2.1 速度控制器设计
假设速度控制输入Φ受到如下饱和约束:
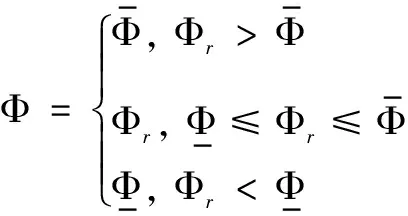
(8)

定义速度跟踪误差eV=V-Vd,并为eV设计如下改进预设性能:
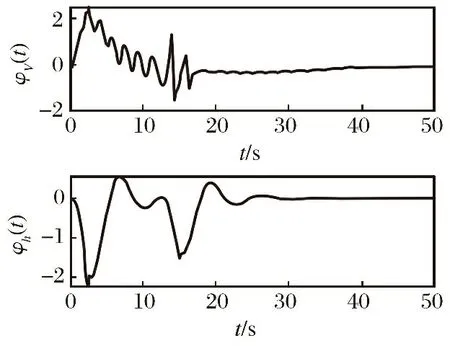
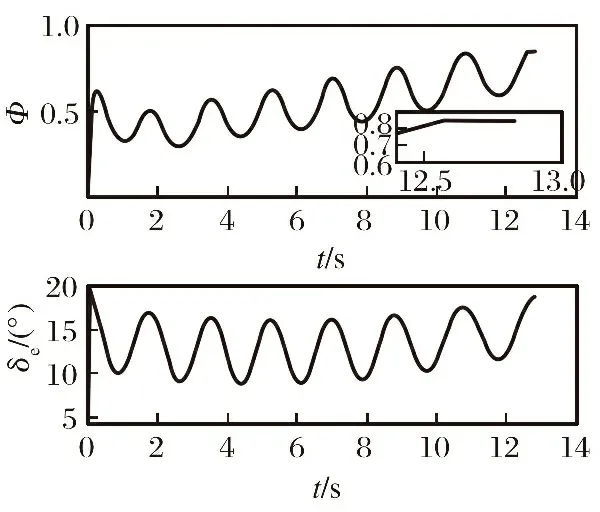
-σV(t)-ϖV(t) (9) 式中: ϖV(t)=bΦtanh(|xΦ|)。 其中,aV>1,σ0,VσV(0)∈R>0,σ0,V>σTs,V∈R>0,Ts,V∈R>0,bΦ∈R>0为待设计参数;xΦ∈R为补偿系统的状态。 注释2:通过为Φr设计合适的反馈控制律使得eV始终位于约束包络(即式(9))内,则为σV(t)∈R>0,ϖV(t)∈R≥0选取合适的设计参数,能够保证eV收敛过程具备满意的动态性能与稳态性能。σV(t)为传统的有限时间收敛性能函数[12],可以确保eV在时间Ts,V内收敛到稳态。ϖV(t)为新设计的自适应调整项,能够根据Φ的饱和情况自适应调整约束包络的形状,使得当执行器饱和时eV始终位于约束包络之内,从而避免传统PPC可能导致的控制奇异问题。 鉴于式(9)不便于控制器设计,定义转换误差: (10) 式中:φV(t)∈R。 对式(10)求导并代入式(1),可得 (11) 式中: rV=1/[2σV(t)+2ϖV(t)]×(1/{eV/[σV(t)+ϖV(t)]+1}-1/{eV/[σV(t)+ϖV(t)]-1})>0; 为了处理速度控制输入饱和问题,设计补偿系统: (12) 式中:aΦ∈R>0;δV∈R>0。 利用xΦ对φV(t)进行修正,得到修正误差: ψV=φV(t)-xΦ (13) 式中:ψV∈R。对式(13)求导,代入式(11)与式(12)并利用ΔΦ=Φ-Φr,可得 (14) 对于未知函数ΞV,引入RBFNN对其逼近: (15) 将Φr设计为 (16) (17) 式中:λV∈R>0。 下面,分析速度子系统的稳定性。 (18) 定义Lyapunov函数: (19) 对式(19)求导并代入式(17)~(18),可得 (20) 考虑到 则有 (21) 定义紧集: 定义高度误差eh=h-hd。为eh设计如下改进预设性能: -σh(t)-ϖh(t) (22) 式中: ϖh(t)=bδetanh(|xδe, 1|+|xδe, 2|+|xδe, 3|)。 其中:ah>1,σ0, hσh(0)∈R>0,σ0, h>σTs, h∈R>0,Ts, h∈R>0,bδe∈R>0为设计参数;xδe, 1∈R,xδe, 2∈R,xδe, 3∈R为辅助系统的状态。 定义转换误差: (23) 对式(23)求导并代入式(2),可得 (24) 式中: rh=1/[2σh(t)+2ϖh(t)]×(1/{eh/[σh(t)+ϖh(t)]+1}-1/{eh/[σh(t)+ϖh(t)]-1})>0; 将航迹角参考指令选为 (25) 式中:lh, 1∈R>0,lh, 2∈R>0为待设计参数。 式(3)~(5)为严格反馈形式,传统方法是采用反演策略设计控制律。但是,反演控制的回馈递推设计过程非常复杂,且存在微分项膨胀问题[11, 15]。为了避免繁杂的反演设计过程,将式(3)~(5)等价变换为[6, 16] (26) 式中:x1=γ∈R;x2∈R;x3∈R;Fh为未知的连续可微函数;κδ>∂Fh/(2∂δe)为常数。 注释3:经过模型等价变换,式(3)~(5)的未知函数Ξγ与ΞQ被归一化为一个总的未知函数Fh,这样仅需要一个RBFNN对Fh进行逼近,降低了神经逼近计算量。 假设高度控制输入δe受到如下约束: (27) 设计新型辅助系统对高度子系统的控制饱和度进行补偿: (28) 式中:xδe, 1∈R,xδe, 2∈R,xδe, 3∈R为辅助系统的状态;δh∈R>0,aδe, 1∈R>0,aδe, 2∈R>0,aδe, 3∈R>0为待设计参数。 定义跟踪误差: sγ=γ-γd=x1-γd (29) 利用辅助系统的状态xδe, 1∈R, 对跟踪误差sγ进行修正: eγ=sγ-xδe, 1 (30) 定义误差函数: (31) 式中:μh∈R>0。 对式(31)求导并代入式(26)、式(28)~(30),得 (32) 对于未知函数Fh,引入RBFNN对其逼近: (33) 将δe, r设计为 (34) (35) 式中:λh∈R>0。 下面,分析高度子系统的稳定性。 (36) 定义Lyapunov函数: (37) 对式(37)求导并代入式(35)~(36),可得 (38) 考虑到 则式(38)变为 (39) 定义紧集: 注释4:传统PPC[6-10]的约束包络不具备再调整能力,当控制饱和导致足够幅度的误差波动时,极易导致控制奇异,表现出明显的脆弱性缺陷。本文提出的改进约束包络含有两个再调整项ϖV(t)与ϖh(t),使得约束包络能够根据误差波动情况自适应调整其形状(增加上包络,减小下包络),从而避免了控制奇异问题,克服了传统PPC的脆弱性缺陷。 为验证所设计控制律、补偿系统以及自适应律的效果及相对于现有方法[14, 17]的优势,以式(1)~(7)作为被控对象,采用MATLAB/Simulink软件进行数值对比仿真。仿真采用四阶龙格-库塔法进行解算,仿真步长为0.01 s。设计参数取值为:aV=2,σ0, V=5,σTs, V=0.5,Ts, V=5,bΦ=2.5,aΦ=1.5,δV=0.8,lV, 1=0.2,lV, 2=0.8,λV=0.05,ah=2,σ0, h=3,σTs, h=0.5,Ts, h=2,bδe=1 000,lh, 1=2,lh, 2=0.8,δh=0.8,aδe, 1=0.5,aδe, 2=1,aδe, 3=1,μh=7,lh=50,λh=0.05,κV=1.2,κδ=1.1。 仿真过程中,假定系统参数随时间摄动±30%,并取典型变化规律为sin(0.1πt)。假定控制输入受到如下约束:Φ∈[0.05, 0.85],δe∈[-18.5°, 18.5°]。分别在以下三种情景进行仿真。 情景1:采用所提方法进行仿真。仿真结果如图2~6所示。图2~3表明,所提方法能够将速度跟踪误差与高度跟踪误差限定在预设的约束包络内,速度跟踪误差与高度跟踪误差均满足期望的动态性能与稳态性能。进一步,当控制输入处于饱和状态时(见图4),速度跟踪误差与高度跟踪误差均有所增加(见图2~3),所提PPC方法的约束包络能够准确感知跟踪误差的增加态势并及时调整约束包络的形状(增加上包络并减小下包络),从而避免了控制奇异。图5~6表明,神经网络权值估计参数与转换误差均有界。由此可见,仿真结果证明了所提方法的有效性。 图2 所提方法的速度跟踪效果 图3 所提方法的高度跟踪效果 图4 所提方法的控制输入 图5 所提方法的神经网络取值估计参数 情景2:只考虑速度控制输入饱和,并取Φ∈[0.05, 0.85];其他条件与情景1完全相同。采用文献[14]的传统PPC约束包络,仿真结果如图7~10所示。由仿真结果可见,速度执行器饱和导致速度跟踪误差增加(见图7、图9),由于文献[14]的传统PPC约束包络没有再调整功能,导致速度跟踪误差因为自身增加而到达了预设包络(见图7),速度子系统的转换误差急剧发散(见图10),最终造成控制奇异,控制系统失效。从而证明了所提方法相对于文献[14]方法的优越性。 图6 所提方法的转换误差 图7 文献[14]方法的速度跟踪效果 图8 文献[14]方法的高度跟踪效果 图9 文献[14]方法的控制输入 图10 文献[14]方法的转换误差 情景3:在不考虑输入受限的情况,将本文所提方法与文献[17]的传统神经控制方法进行对比。仿真结果如图11~12所示,两种方法的稳态精度基本相当。由图11可见,相对于文献[17]方法,所提方法的速度误差的超调量虽有所增加,但仍然满足期望的预设性能。但是,在高度跟踪方面,所提方法保证了高度跟踪误差更小的超调量(见图12)。进一步,所提方法相对于文献[17]方法 在算法计算量方面的优势具体如表2所示。由表2可见,当两种方法的仿真时间都设置为50 s时,文献[17]方法需要大约44 s的时间才能完成仿真程序的运行,而本文方法完成程序运行只需要大约12 s的时间。 图11 速度跟踪误差对比 图12 高度跟踪误差对比 表2 仿真时间对比 针对WV输入受限条件下的跟踪控制问题,提出了非脆弱神经PPC新方法。将神经逼近与模型变换相结合,避免了传统反演控制的回馈递推设计过程,并降低了控制复杂度与在线学习量。为了处理控制输入问题,设计了新型补偿系统对控制输入饱和度进行补偿。利用补偿系统的状态对传统PPC的约束包络进行改进,进而为WV的速度跟踪误差与高度跟踪误差设计了新型非脆弱约束包络。仿真结果表明,存在输入受限条件下,所提方法仍能保证跟踪误差期望的预设性能,并能克服传统PPC的脆弱性缺陷。鉴于在仿真初始阶段存在较大的控制输入,后续研究将在借鉴文献[18-20]研究结果的基础上,深入研究对数函数与控制输入速率约束等因素对控制输入初值的影响问题。

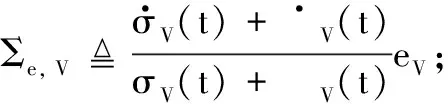
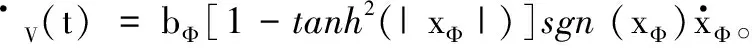


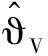
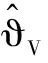

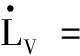

2.2 高度控制器设计
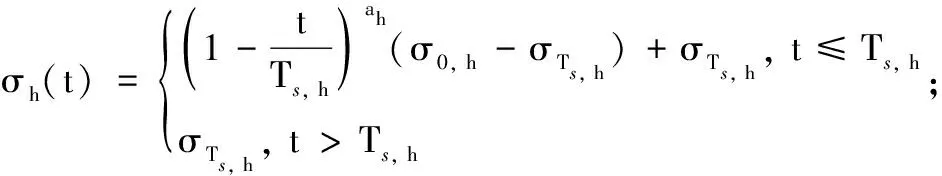

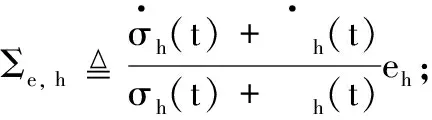



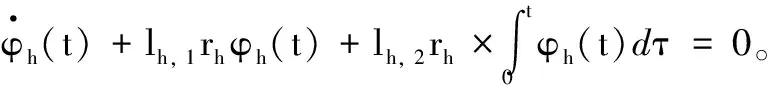
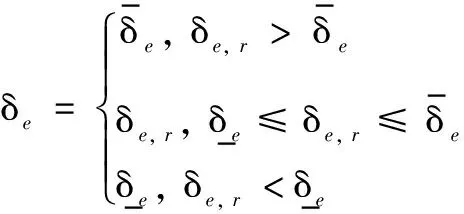
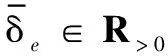
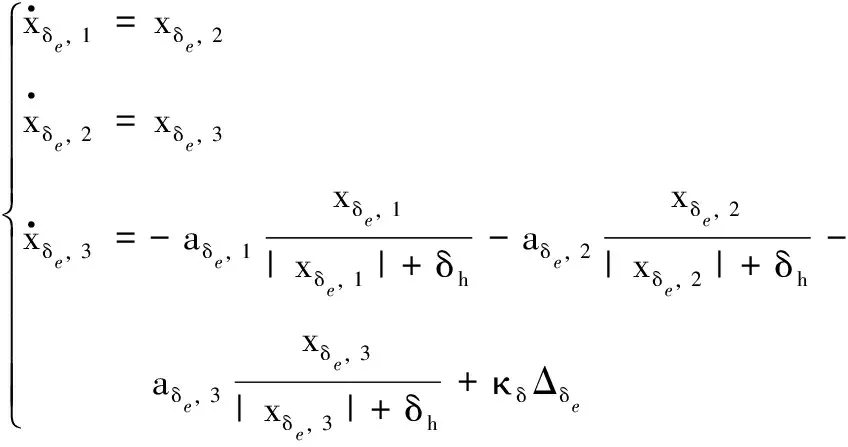


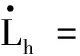

3 数值仿真与分析










4 结 论
