面向高机动目标拦截任务的空空导弹制导方法综述

纪 毅，王 伟，张宏岩，范军芳，豆登辉，裴 培

(1.北京信息科技大学 自动化学院，北京 100192；2.北京信息科技大学 高动态导航技术北京市重点实验室，北京 100192；3.北京理工大学 宇航学院，北京 100081；4.北京理工大学 无人机自主控制技术北京市重点实验室，北京 100081；5.西安现代控制技术研究所，西安 710065)

0 引 言

空空导弹指由战斗机、无人机等空基平台发射的攻击飞机、战略战术导弹、低轨卫星或临近空间飞行器的弹药武器系统，是拦截敌对目标、完成防空反导任务、保障空天安全的难以替代的有力武器。与地基、海基导弹以及机载定向能武器相比，空空导弹具有以下优势：飞行速度更快，机动性更强，发射平台兼容性强；系统部署区域广泛，作战方式灵活；作战高度更高，效率更高；目标匹配性高[1-2]。

当今世界正经历“百年未有之大变局”，给国土安全带来全新挑战。随着世界新军事革命的深入发展，以美国为首的西方军事强国在第五代战斗机、巡飞弹、弹道导弹等一系列高速飞行武器领域取得重大突破[3-4]。针对大气层内高速飞行目标的防空反导任务，正成为国防事业不可或缺的一环。随着高速飞行武器技术不断发展，防空反导任务对具有精确制导能力的空空导弹的需求越来越迫切，主要体现在：(1)高速飞行目标飞行包络更广，飞行轨迹复杂，飞行状态多变，难以实时预测，传统飞行模式难以满足目标动态追踪的需求；(2)高速飞行目标复杂的运动状态使末制导段弹目视线角呈不确定性时变状态，对空空导弹鲁棒性与抗扰性提出要求；(3)高速飞行目标过载呈现高频大幅震荡状态，为实现精准拦截，空空导弹的控制系统与执行机构需快速精确地提供对应的过载。为此，亟需研发能实现对目标轨迹的准确预测与精确拦截的制导技术，以综合提高空空导弹的制导性能，完成针对高机动目标的精确制导任务，满足复杂战场环境下的精确防御需求。

提前预判高速飞行目标的攻击意图，据此预测其运动轨迹，可为空空导弹的战术决策提供依据，有利于提升其拦截成功率。海湾战争中，面对伊拉克军队“飞毛腿”导弹的攻击，美军总是要发射数倍数量的“爱国者”导弹进行拦截，但拦截成功率仅为40%[5]。其原因一定程度上在于对对方高速飞行器攻击意图和运动轨迹的判断不明，而不得不在其飞行轨迹各区域中分别进行拦截。相比于30年前的“飞毛腿”导弹，未来战争中高速飞行目标将拥有更大的可用过载和更强的离轴运动等性能，轨迹灵活性将有明显提升。为提高作战效费比，挖掘空空导弹的潜能，优化战术决策，提高拦截效果，有必要研究高速飞行目标的轨迹预测技术[6-8]。

高速飞行目标瞬时过载巨大，运动状态变化剧烈且具有强非线性与强不确定性，弹目视线角速率具有高频大幅震荡特征，且随着弹目距离的接近而愈发增强，在空空导弹的末制导段逃逸能力极强[9]。传统制导弹药采用的比例导引类制导律推导自线性制导动力学模型，难以跟踪高机动非线性目标，且末端过载过大的现象时有发生，严重限制了末制导效果[10]。此外，考虑高速飞行器运动状态时变以及末制导段弹目距离较近等因素，诸如数学模型不确定性、气动参数漂移、目标运动估测误差等微小扰动亦会对弹目视线角速率的获取产生较大影响。因此，有必要研究具有抗干扰自主追踪能力、可根据高速飞行器的运动状态实时计算对应的制导指令的高精度强鲁棒末制导技术。

对隐形目标的突发性打击任务要求空空导弹具有对制导指令快速高效的响应能力。经典双回路制导控制结构忽略了制导与控制回路间的兼容性，基于频谱分离原则分别设计制导与控制系统。然而在末制导段，较小的弹目相对距离导致空空导弹制导回路的带宽逐渐增大，制导系统与控制系统之间的关系难以协调，进而导致其过载指令得不到快速高效的执行，严重限制了空空导弹的制导指令响应与过载能力[11]。为消除经典双回路制导控制系统中制导回路与控制回路间的不兼容性，有必要开展制导控制一体化系统与算法的相关研究。

综上所述，正是在针对高速飞行器的迫切拦截需求与空空导弹实际工程背景的牵引下，面向日趋复杂的战场环境，本文对高速飞行目标意图识别与轨迹预测问题、末制导段空空导弹目标逃逸与扰动抑制问题、临近目标时制导指令快速高效响应问题进行深度调研，并对上述问题的现有解法进行综述，对需要进一步研究的问题进行展望。

1 典型先进空空导弹简介

空空导弹是从空中发射、攻击空中目标的导弹[1]。从20世纪40年代问世以来，已历经四代重大革新，逐渐成为空战的主要武器。在近80年的发展历程中，空空导弹逐步实现“质量轻型化、外形细长化、射程远程化、轨迹灵活化”，由第一代、第二代的“追尾式”攻击方式过渡至第三代、第四代的“全向式”攻击方式，其发展历程如图1所示[2]。

图1 四代空空导弹发展示意图[2]

根据制导体制差异，空空导弹可分为红外制导型空空导弹和雷达制导型空空导弹两大类。其中，红外制导型空空导弹具有体积小、重量轻、成本低、使用方便、维护便捷、不依赖于机载雷达数据链系统配合、适用于小型廉价战斗机装配等优势[1]。但受其制导体制限制，红外型空空导弹仅适用于射程小于20 km的近程拦截任务。雷达制导型空空导弹虽不具备上述优势，但其射程通常可达35～80 km，部分雷达制导型空空导弹射程可达160 km，有利于战斗机战场生存和执行中远程拦截任务，具有十分重要的作用。

“响尾蛇”AIM-9X近战空空导弹是第四代红外制导型空空导弹的典型代表，是“响尾蛇”导弹家族中最新改进型，其结构如图2所示。不同于“响尾蛇”空空导弹家族中其他任何型号弹药，AIM-9X导弹弹身细长，只有四个前置固定翼与四个很小的矩形尾翼。此外，取消了陀螺舵的设计，使用专用的姿态控制系统来确保弹体在飞行过程中不会发生自旋。该导弹具有大离轴角拦截与发射能力，可以在±90°视场范围内寻找目标, 在严重杂波和红外干扰环境下仍可实现精准打击。

图2 “响尾蛇”AIM-9X近战空空导弹

在制导系统方面，AIM-9X导弹采用先进的红外自寻的制导系统，导引头采用图像增强红外焦平面阵。不同于普通红外制导导弹，AIM-9X导弹的数字化制导系统可以选择攻击目标的薄弱部分，而非直奔目标发热量最大的发动机尾喷口。通过与最新型联合头盔瞄准系统(JHMCS)交联并配备新型三维喷气矢量系统，AIM-9X导弹具备比配备传统制导系统的导弹优异得多的转向能力。利用头盔瞄准具，飞行员只要注视着敌机就可以使该导弹飞向目标。

在控制系统与执行机构方面，AIM-9X 导弹采用了先进的自动驾驶仪系统，具有很强的机动控制能力；采用矢量控制系统，通过改变发动机尾燃气舵喷口喷气方向来控制导弹的飞行方向，从而让导弹有了更加敏捷的飞行能力；采用了尾部控制翼设计，缩小了弹翼面积，以适应F-22“猛禽”战斗机的弹舱容积限制。

“AMRAAM”AIM-120D中程空空导弹是第四代雷达制导型空空导弹的典型代表，其结构如图3所示，是美军产品改进计划(P3I)的第四代产品。其改进主要包括采用GPS辅助惯导与双向数据链，增大离轴发射角，改进制导软件以改善运动学性能，扩大了不可逃逸区，将射程提高50%，提高了电子扰抗能力，进一步提高导弹的精度、射程、杀伤力和生存能力。

图3 “AMRAAM”AIM-120D中程空空导弹

AIM-120D导弹的一大特色是采用了空空导弹中罕见的基于卫星-惯性组合导航系统的弹道中段补偿方法。该方法可减少惯导系统的误差，提高路径规划效率，进而节约能量，在无需对发动机进行改进设计的条件下提高射程，使其达到160 km。同时，该方法可降低导弹的对准误差，提高导弹的制导精度。

AIM-120D导弹的另一大特色是采用了双向数据链路通讯系统。弹体前部装有共形天线，支持导弹与母机间双向通信功能。这使得导弹可以成为空中打击网络的一个节点，既可以补充预警飞机和战斗机雷达的探测范围，又可以作为空中作战网络体系的一个传感器，实现武器、火控、指挥、探测、决策之间的无间隔交连。双向数据链路通讯还可以使导弹被载机发射后，由另一架战斗机控制其飞行状态，此时，载机可以立即脱离，进入下一个作战空域。

2 典型空空导弹制导方式与关键问题

空空导弹制导过程主要包括战术决策段、初始段、中制导段、中末制导交接段、末制导段、目标交会段。其中，中制导段和末制导段的效能直接决定空空导弹能否精准命中目标。中制导的作用是控制弹体平稳飞行至导引头的探测范围内(通常不大于25 km)，末制导的作用是将弹体精准导引至目标，以实现精确拦截。

制导控制系统是空空导弹实现精确拦截的核心，通常由目标运动探测器(Seeker)、中央处理器(Center Processing Unit，CPU)、自动驾驶仪(Autopilot)和执行机构(Actuator)组成(也有资料将执行机构视为自动驾驶仪的组成部分[12])。各组部件简介如表1所示。

表1 空空导弹制导控制系统各组部件简介

此外，部分空空导弹(如AIM-120D)存在GPS/INS辅助制导系统。该系统虽不可独立作用于制导指令生成，仍需依赖雷达或红外探测系统，但可实时生成导弹位置信息，提供参考弹道，有利于空空导弹中制导飞行增稳增程。

空空导弹制导控制系统的工作流程如图4所示。首先，目标运动探测模块工作，探测高速飞行目标的位置、速度等信息。对于超视距攻击的雷达型空空导弹，该过程通常发生在导弹点火前，即机载雷达需提前锁定目标位置，并将该信息装订至火控系统。对于红外型空空导弹，通常由飞行员瞄准目标之后，目标位置信息被发送给弹载计算机，由中央处理器实时解算弹目相对位置信息(该信息通常为弹目视线角速率)，并将其作为制导律的输入量，以生成需用过载。该过载指令被输送至自动驾驶仪，解算出执行机构指令，控制执行机构工作，进而改变弹体动力学，实现精准拦截。

图4 空空导弹制导控制系统的工作原理示意图

空空导弹的制导流程如图5所示。在空空导弹实际应用中，下述制导控制问题时常出现，严重影响其拦截效果：

图5 空空导弹制导阶段示意图

(1)高速飞行目标意图识别与轨迹预测问题。高速目标飞行轨迹难以预测，导致空空导弹的制导策略难以确定。该问题常发生于战术决策段与中制导段，可通过设计基于贝叶斯推断(Bayesian Inference)[13-16]的轨迹预测方法解决。

(2)末制导段高速目标逃逸与扰动抑制问题。随着末制导段弹目相对距离的接近，高速飞行目标自身逃逸能力和扰动对弹目视线角速率的影响被放大，导致制导失准。该问题常发生于末制导段，可通过设计非线性强鲁棒制导律[17-18]解决。

(3)临近目标时制导指令快速高效响应问题。空空导弹制导系统与控制系统之间存在时间滞后问题，制导指令难以快速高效执行，导致制导精度降低。该问题常发生于空空导弹临近目标时，可通过设计制导控制一体化系统及算法[19-20]解决。

综上所述，为实现空空导弹对高速飞行目标的精准拦截，需解决高速飞行目标意图识别与轨迹预测问题、末制导段高速目标逃逸与扰动抑制问题、临近目标时制导指令快速高效响应问题。下面就这些问题的国内外研究现状进行分析。

3 目标轨迹预测方法研究现状

高速飞行目标轨迹预测是防空反导领域的重大课题之一，其准确程度直接决定了空空导弹的命中效果，进而影响了我方拦截策略。对我方指战员而言，对方高速飞行器属非合作目标，其运动学与动力学信息无法直接获取，需根据其先验飞行轨迹推测其航向、速度和气动参数等信息。邵雷等[21]将目标的轨迹预测方法分为三类，即基于目标运动机理信息的轨迹预测方法、基于统计学原理的轨迹预测方法、基于目标机动意图的轨迹预测方法。表2对比了上述三种方法的优势与缺陷。

表2 现有目标轨迹预测方法的优势与缺陷

基于目标运动机理信息的轨迹预测方法指利用目标的运动机理信息，建立预测模型而实现轨迹预测的方法。该方法将目标的气动参数、升阻比等运动学特征表述成具有一定规律的关系式，以实现对上述参数的有效估计。王路等[22]认为升阻比是实现轨迹预测的关键，建立运动状态模型，通过函数拟合其升阻比，通过数值积分预测轨迹；张凯等[23]研究了气动参数的变化规律，针对高超声速飞行器目标跳跃的机动特点，设计了一种多层递阶轨迹预测方法，并据此递推目标轨迹；李广华等[24]分析了目标的机动能力及可能存在的机动模式，建立了以攻角和侧滑角为控制量的纵向与侧向动力学模型，并对飞行器的多种机动能力提出评估指标。这一类方法直观描述了高速飞行器的运动学特征，但考虑高速飞行目标运动状态时变性，其参数往往难以准确辨识。

基于统计学原理的轨迹预测方法指在高速飞行目标运动状态的先验信息难以获取的情况下，通过对飞行器历史运动状态的分析，建立相关控制量的概率分布，以获取飞行器轨迹的统计学特征，并据此预测其运动轨迹。Chen等[25]结合参数估计与聚类等方法建立轨迹密度函数，并求其后验概率密度，在一定程度上实现了对不规则运动飞行器的轨迹预测；乔少杰等[26]利用高斯混合模型对不同的运动模式进行建模，基于历史数据，结合高斯回归模型与最小二乘法设计轨迹预测方法；秦雷等[27]设计了卡尔曼滤波器，利用蒙特卡洛仿真试验估计高速目标三轴方向位置与误差。这一类方法采用统计学原理对高速飞行器进行建模，解决了基于目标运动机理信息的轨迹预测方法中因运动模式不匹配、建模与参数估计不准确导致的预测失准问题，但该方法需大数据支撑。考虑实际拦截任务中对方高速飞行器运动状态信息难以实时获取，该方法仍在一定程度上存在局限性。

基于目标机动意图的轨迹预测方法指通过挖掘高速飞行器的目的性获取潜在的目标运动信息，并据此实时补偿飞行器动力学控制模型，以提升轨迹预测精度，其流程如图6所示[22]。通常通过构造目标意图代价函数来评估飞行器目的。张凯等[28]采用贝叶斯推断方法迭代高速目标运动状态，通过意图代价函数分析其机动意图，并通过蒙特卡洛采样方法实现轨迹预测；基于动态贝叶斯网络，罗艺等[29]对高速飞行器与攻击目标间的关系进行推理，以预测高速飞行器的机动意图；文献[30]提出一种基于飞行器机动意图的轨迹预测方法：首先利用多模型算法预测多条飞行器轨迹，根据其意图方向的贴合度分配权重，并利用意图信息平滑上述轨迹。这一类方法对基于统计学原理的轨迹预测方法进行补充，通过目标意图代价函数更精确地获取先验目标轨迹，分析目标意图与准确设计目标意图代价函数是该类方法的关键。

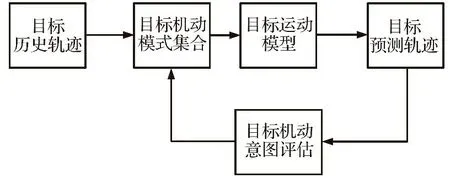
图6 基于目标机动意图的轨迹预测方法流程图[22]

4 制导算法研究现状

作为一种高效的制导律，比例导引(Proportional Navi-gation，PN)制导律[31-32]被广泛应用于针对静止与运动目标的制导任务中。若忽略量测噪声、环境扰动和时间滞后等因素，比例导引制导律可实现零脱靶量的制导效果。当其导航比选取为3时，其形式与能量最优化制导律相同。在工程实践中，根据加速度指令方向定义方式的区别，比例导引制导律可分为纯比例导引(Pure Proportional Navigation，PPN)制导律、理想比例导引(Ideal Proportional Navigation，IPN)制导律和真比例导引(True Proportional Navigation，TPN)制导律。然而，当其应用于高速目标制导任务时，以下两个主要缺点严重制约其性能：(1)比例导引制导律在弹道末段所需过载较大，即需用攻角过大，进而引起空空导弹姿态高频大幅摆动现象，可能导致飞行失稳；(2)由于比例导引制导律推导于线性制导动力学模型，在设计过程中忽略了非线性扰动的影响，导致其自身对非线性扰动抵抗能力较弱，难以适应具有强非线性不确定性的高速目标。

在现代战场中，零脱靶量不再是评估制导律性能的唯一指标。制导过程需满足多约束条件，如最小能量消耗约束、终端角度约束和飞行时间约束等。因此，最优控制和优化理论[33-36]被广泛应用于制导律设计，在实现增程与精确制导的同时满足上述约束条件。文献[37]设计了一种考虑小扰动和飞时落角约束条件的最优制导律；何绍溟等[38]通过施瓦兹不等式(Schwarz’s Inequality)推导出一种最优误差动力学函数，并利用其分别设计零化弹目视线角速率、落角约束、飞时约束和直接碰撞制导律；文献[39]设计了一种可直接利用重力补偿的新型最优制导律，通过重力转向以降低能量消耗。上述最优制导律可分为两类：线性与非线性最优制导律。前者可得出能被执行机构实时执行的解析形式为加速度指令，但制导动力学模型非线性特征的缺失可能引发诸多问题；后者需要大量的计算资源来求得并仅能求得数值近似解，这导致其仅能应用在导弹发射前，而无法在导弹飞行过程中根据其状态实时调节。除上述最优制导律之外，一些衍生比例导引制导律(如偏置比例导引制导律[40-42]和变增益比例导引制导律[43])同样可以达到角度收敛的效果。与线性最优制导律相同，上述制导律同样由线性动力学制导模型推导，难以适应高速目标的非线性机动特性。

针对高速目标，已公开的文献中存在大量的基于先进控制理论的制导律。考虑到弹目视线角速率无法直接量测的工况，He等[44]提出一种基于几何同质性(Geometric Homogeneity)和李雅普诺夫理论的观测器来估测弹目视线角速率，并设计了一种鲁棒有限时间收敛制导律；为消除不确定边界和未知干扰对制导精度的不利影响，Yang等[45]将无法预测的目标机动性视作有界未知量，设计了基于H∞控制理论的鲁棒制导律；文献[46]提出一种输入状态稳定(Input-to-State Stability)制导律来限制有界的目标机动性，并对有界的弹目视线角速率进行估测；文献[38]利用施瓦兹不等式推导了一种弹道成型制导律(Trajectory Shaping Guidance, TSG)，文献[47]求得其解析解。

此外，二阶滑动模态控制(Second-Order Sliding Mode Control，2-SMC)理论[48-51]被视为设计针对高速目标终端角度制导律的“有力工具”，因为其具有强鲁棒性、全局收敛性和可降阶性，通过合理地构建包含一阶与二阶系统状态量(制导律设计中指弹目视线角与角速率)的滑模面，即可实现全局稳定，从而使导弹按照特定终端角度精准命中目标。在文献[52]，一种未展现出任何奇异性(Singularity)平面滑模制导律被提出；结合非奇异终端滑模(Nonsingular Terminal Sliding Mode，NTSM)、平滑二阶滑模和有限时间扰动观测器，He等[53]提出一种连续非奇异鲁棒制导律来应对位置的目标机动；Si等[54]设计了可削弱抖振的三维自适应制导律，在考虑输入饱和的条件下，其解析形式在文献[55]中给出；为处理无法预测的目标逃逸策略，Zhang等[56]提出一种包含二阶同质性观测器的鲁棒有限时间收敛制导律；文献[57]给出一种基于指令性能函数(Prescribed Performance Function)的控制方法，可使滑模面平滑地收敛至零，并据此设计了角度约束制导律。

表3给出了上述制导方法在高动态目标追踪能力、能量最优化、落角约束能力、鲁棒性、工程实用性等方面的性能对比。

表3 现有制导方法性能对比

从上述研究现状可以看出，非线性制导律更适合拦击具有强非线性不确定性的高速目标，强鲁棒制导律可抵御末制导段因目标运动特性和其他因素产生的扰动。基于滑动模态控制理论的制导律兼具非线性和强鲁棒性，亦具有有限时间收敛性，适宜设计末制导律。

5 制导控制一体化系统与算法研究现状

为实现对高速目标难以预测的运动状态的实时跟踪，空空导弹往往需配置能够快速执行制导指令的制导与控制系统。传统导弹装配有经典双回路制导控制系统，即制导系统与控制系统分别设计，独立工作，其工作频率往往不一致，进一步导致制导指令难以被快速、准确、直接地执行。

在此背景下，系统考虑导弹的外部制导需求和内部控制组件的特性，兼顾导弹制导系统与控制系统之间的不兼容性，制导控制一体化(Integrated Guidance and Control，IGC)系统在降低系统设计成本和系统保守性的同时，挖掘了空空导弹制导控制组部件的潜力，提高导弹在末制导过程中的机动性，有利于降低空空导弹制导控制系统的研发成本，提高制导控制系统的稳定性。

根据内回路的不同结构，对制导控制一体化系统与算法的研究广义上可分为三大类：考虑自动驾驶仪动力学特性的制导律设计[9, 58-59]、完全制导控制一体化系统与算法设计(Full Integrated Guidance and Control，FIGC)[60-61]和部分制导控制一体化系统与算法设计(Partial Integrated Guidance and Control，PIGC)[62-65]，如图7～9所示。考虑自动驾驶仪动力学特性的制导律设计将导弹自动驾驶仪视作一个一阶惯性动力学环节或二阶振荡动力学环节，考虑了控制器特性，降低了设计难度。尽管有时考虑自动驾驶仪动力学特性的制导律具有较好的效果，但该描述方式不够准确，并不能完全适用于高速目标。完全制导控制一体化打破了制导回路与控制回路之间的壁垒，综合考虑末制导过程中的各种因素，逐步设计控制量。尽管该方法可以彻底解决时间滞后、频率不协调与兼容性不足等问题，但该方法要求弹体有着充裕的动态稳定裕度以抵消严重的气动扰动。部分制导控制一体化系统改造了传统的制导控制双回路结构，其外回路包括目标运动信息捕获系统与运动学制导系统，而内回路仅为执行机构与弹体动力学环节。与完全制导控制一体化系统及算法设计相比，因其保留了双回路结构，制导控制一体化系统与算法更易设计与执行。

图7 考虑自动驾驶仪动力学特性的制导控制系统示意图[60]

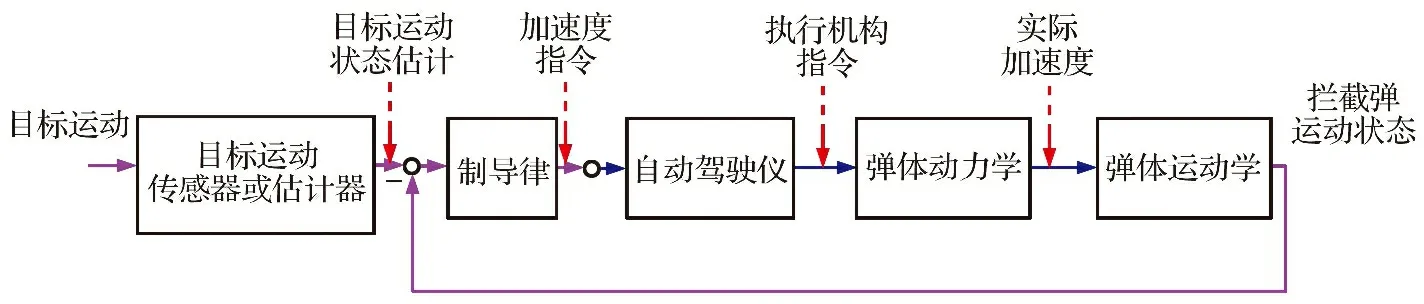
图8 完全制导控制一体化系统示意图

图9 部分制导控制一体化系统示意图

近几十年来，已公开的文献中存在大量制导控制一体化系统与算法。随首先进控制算法，如模型预测控制(Model Prediction Control，MPC)、状态独立黎卡提方程(Sate-Dependent Riccati Equation，SDRE)、反馈线性化、有限阶段最优控制、θ-D方法、反步法(Backstepping)与滑动模态控制(Sliding Mode Control，SMC)等方法的引入，为制导控制一体化系统与算法的发展做出了大量贡献。利用连续时间预测控制技术，Panchal等[66]设计了一种最优制导控制一体化算法，其特征在于目标加速度信息可以通过状态扩张观测器获取；结合动态面控制理论和扰动观测技术，Wang等[67]提出一种可成功应用于多导弹协同制导的新型制导控制一体化系统；通过非线性坐标转换矩阵来调整系统状态方程至标准形式，Chwa等[68]提出一种考虑控制回路动力学特性的自适应制导算法；考虑到应用侧喷控制方式的导弹的典型动力学特性，Chen等[69]将制导控制一体化思想引入一个理想的参考模型。此外，文献[60，63]讨论了攻击角度约束条件下的典型制导控制一体化设计方法。具体而言，文献[60]针对零控脱靶量(Zero-Effort Miss，ZEM)设计了四阶反步控制方法；文献[63]将上述问题视为一个高阶系统收敛问题并设计滑模控制器。

值得注意的是，在已公开的文献中，基于滑模控制理论的制导控制一体化设计方法占据绝大部分。因其具有强鲁棒性，滑模控制技术被广泛应用于制导控制一体化系统及其他领域，如导弹制导律、无人机(Unmanned Air Vehicle，UAV)自动驾驶仪、机械臂控制系统和微机电(Micro-Electro-Mechanical System，MEMS)陀螺等。在滑模控制技术的应用中，控制量抖振和系统奇异性是两个亟需解决的重要问题。近年来，相当数量的新型滑模控制理论被提出以解决上述两个问题，文献[70-75]给出了解决上述问题的理论方法和一些实际应用。基于此，一些学者提出独特的制导控制一体化方法来适应不同的应用环境。如He等[60]提出基于自适应非奇异扰动观测器(Nonsingular Disturbance Observer，NDOB)的三维多变量制导控制一体化设计方法；Wang等[62]提出适用于一系列非线性制导动力学模型的自适应终端滑模算法，并基于此设计了部分制导控制一体化系统；Song等[74]设计了一种基于新型动态面的制导控制一体化算法；基于Super-twisting算法，Lai等[75]在三维空间中设计了一种部分制导控制一体化算法，该算法可实现弹目视线角有限时间收敛。

总之，为降低空空导弹制导系统与控制系统间的时间滞后与不兼容性，提高制导控制效率，需要研究制导控制系统一体化设计方法，充分发挥各组部件潜力，以使空空导弹能够快速高效地执行制导指令。

6 目标预测与制导方法研究展望

考虑到上述目标预测与制导方法的工程适用性，为进一步解决高速飞行目标意图识别与轨迹预测、末制导段空空导弹目标逃逸与扰动抑制、临近目标时制导指令快速高效响应等问题，提升空空导弹的制导控制性能，以下问题仍需进一步研究：

(1)结合运动机理、统计学与目标意图的综合轨迹预测方法

目标轨迹预测是空空导弹面向未来战场的方法之一，然而目前已公开的轨迹预测方法均存在一定局限性。其中，基于目标运动机理的轨迹预测方法缺乏对目标运动状态突变的适应性；基于统计学理论的轨迹预测方法需要大量的同型号目标飞行数据；基于目标意图的轨迹预测方法需要短时间内实现对目标意图的精准研判。将上述三种方法按照一定科学规律有机结合，扬长避短，不失为目标轨迹预测方法的有效研究方向。

(2)非线性在线近最优制导方法

为了在不改变空空导弹结构的条件下增加其射程，需对空空导弹的能量进行优化。能量最优控制法基于线性化模型设计，虽可在线实时解算制导指令，但忽略了非线性气动特征对空空导弹制导系统的影响；非线性数值优化法充分考虑了系统的非线性特征，但弹载计算机难以满足其所需的计算能力，故无法在飞行过程中在线运算。研发可在线应用的非线性近最优制导方法，兼具前沿探索与工程实践意义。

(3)非线性制导方法的工程化应用

目前，已公开的文献中存在大量以滑模控制、反步法、李雅普诺夫、自抗扰控制为基础的非线性制导方法。上述方法结合了现代控制理论，兼具自适应性与强鲁棒性，可有效抵御外界未知不确定因素对制导过程的干扰。然而，上述方法往往形式复杂，参数繁多，难以在工程实践中得到有效应用。简化上述制导方法的形式，明确各参数的物理意义，提出简明的参数选取准则，是实现非线性制导方法工程化设计与应用的重要研究内容。

(4)智能化制导方法

近年来，计算机性能的飞速提升大大强化了智能化制导方法的应用前景。以深度学习、强化学习为代表的智能化图像识别算法具有高精度识别目标的能力，且敏感同一类型的目标；以YOLO算法为代表的快速目标识别方法契合高机动目标的拦截任务。智能化制导方法的进一步发展与工程化移植应用，是空空导弹制导领域的重要课题。

(5)容错制导控制方法

在空空导弹的飞行过程中，不稳定空气动力学环境时常存在，会引发难以忽略的干扰，如大范围气动参数摄动、执行机构故障或输入饱和、雷达定位失准、数据链延迟过高等。上述问题往往引发制导控制错误，严重影响了空空导弹的制导控制效果。目前已有文献通过观测器、强化学习等方法实现故障检测与故障分离，通过强鲁棒容错控制方法实现容错控制，但如何将其移植应用于空空导弹，仍需进一步探索。

(6)制导控制一体化方法的工程实现

制导控制一体化方法的优势在于对目标机动的快速响应，将绕质心运动的影响因素引入到质心运动控制中，规避了临近目标时刻的频带耦合问题。大量文献从不同角度阐述了这一方法的设计思路，并给出相应的仿真结果。然而，其工程实现方法仍需通过半实物仿真试验、工程样机地面试验、飞行试验等手段进一步探索。

7 总 结

现代及未来战争的发展态势对空空导弹提出了目标动态追踪、强鲁棒性和高抗扰性、面对目标机动的快速精准响应等全新要求，带来了高速飞行目标意图识别与轨迹预测、末制导段高速目标逃逸与扰动抑制、临近目标时制导指令快速高效响应等问题。针对上述问题，本文深度调研了目标轨迹预测方法、制导算法以及制导控制一体化方法，对比分析了各种方法的优势与缺陷，结论如下：

(1)三种目标轨迹预测方法各有利弊。基于目标运动机理的轨迹预测方法具有可解释性，但对于飞行参数的实时性与准确性要求较高；基于统计学原理的轨迹预测方法不敏感于飞行参数，但需要大量历史数据支撑，对全新或突变飞行环境的适应性差；基于目标机动意图的轨迹预测方法的精度取决于对目标意图的精准研判。综合上述三种方法的轨迹预测方法，不失为该领域的有效研究方向。

(2)制导算法方面，比例导引制导律简单实用，但其忽略了非线性扰动项，鲁棒性有限；非线性优化制导律优化效果良好，但其难以在线解算制导指令，对气动参数突变环境适应性差；滑模制导律以高能耗为代价换取强鲁棒性与抗扰动能力，且制导指令存在高频抖振；新型高阶非线性制导律解决了抖振问题，但其参数繁多，难以应用于工程实践。

(3)制导控制一体化方法的优势在于降低空空导弹制导系统与控制系统间的时间滞后与不兼容性，提高了制导控制效率，但目前其工程实现方法仍需进一步探究。