数学思想：“是什么”与“怎么做”

苏明强

在小学数学教学中渗透数学思想这一目标要求，在我国主要经历了萌芽、发展和成熟三个阶段。1978年颁布的《全日制十年制学校小学数学教学大纲（试行草案）》，首次提出了“初步了解现代数学中的某些最简单的思想”的目标要求，强调“通过直观，使学生尽早接触集合、函数、统计等一些现代数学的思想”。《全日制义务教育数学课程标准（实验稿）》再次把“基本的数学思想方法”列入课程总体目标中。《义务教育数学课程标准（2011年版）》提出“四基”的目标要求，数学思想发展是“四基”的重要内容。《义务教育数学课程标准（2022年版）》则继承了“四基”的目标内容。经过近10年的研究与实践，我国学者普遍认为，数学基本思想包括抽象思想、推理思想和建模思想，数学思想可以看做是数学基本思想的下位概念。那么，数学思想是什么？如何在教学中渗透数学思想？

数学思想是数学知识和数学方法在更高层次上的抽象与概括，数学思想常常蕴含在数学知识的形成、发展和应用过程中。教学时，我们应该从数学思想的角度分析教材，挖掘隐藏在数学知识背后的数学思想，将其列入教学目标，并在教学过程中进行渗透。

比如，教学小数的认识时，教师可借助“数线”，渗透数形结合思想和对应思想，让学生通过寻找1、0.1、0.01的“家”，感受比1小的计数单位在数线上的对应位置；通过“数一数”渗透变中不变思想，让学生发现计数单位变了，相邻计数单位之间的进率不变，体会数本质的一致性；通过“分一分”渗透分类思想和集合思想，让学生发现可以按照小数点后面有几位，把小数分为一位小数、两位小数等；还可以通过“想象”渗透极限思想，让学生发现0.001、0.0001等越来越接近0，但是始终不会等于0。一般地，在数学知识的形成过程中，主要蕴含的数学基本思想是抽象，具体包括分类思想、集合思想、对应思想、符号表示思想、数形结合思想、变中不变思想、极限思想等。因此，我们在数概念、运算概念与定律、图形概念、度量概念、统计量等知識的教学中，要注意渗透抽象思想。

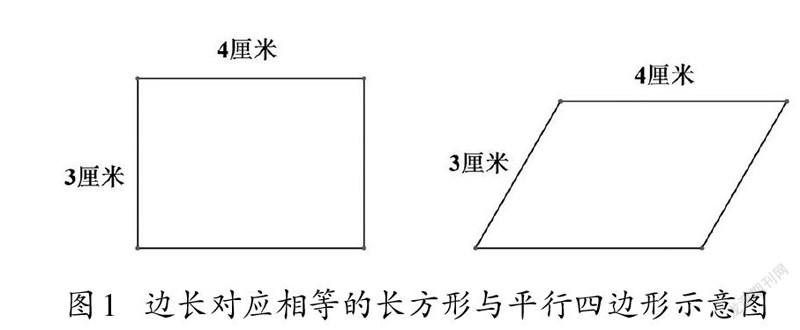
比如，教学平行四边形的面积时，教师可以通过“割补”把平行四边形转化成长方形，渗透转化思想；在公式推导过程中，可以通过“比较”让学生发现平行四边形的底和高与转化后长方形的长和宽之间的关系，凭借推理得出结论，渗透演绎思想；还可以通过“猜测”让学生思考其他图形的面积会与哪些量有关，渗透类比思想。一般地，在数学知识的发展过程中，主要蕴含的数学基本思想是推理，具体包括转化思想、归纳思想、类比思想和演绎思想等。因此，我们在数的性质、数的运算、图形性质、周长公式、面积公式、体积公式等知识的教学中，要注意渗透推理思想。

比如，教学折线统计图时，教师可以通过引导学生一起研究汽车的速度与时间的变化规律，让学生经历收集数据、整理数据、表达数据和分析数据的过程，渗透量化思想、函数思想、随机思想和统计思想。一般地，在数学知识的应用过程中，主要蕴含的数学基本思想是建模，具体包括简化思想、量化思想、优化思想、方程思想、函数思想、随机思想、统计思想等。因此，我们在数与代数、图形与几何、统计与概率等知识的教学中，要注意渗透建模思想。

总之，感悟数学思想是形成核心素养的重要途径。我们应该养成从数学思想的角度分析教材的习惯，在教学中适时加以渗透，这样才能更好地促进学生核心素养的形成与发展。

（泉州师范学院教育科学研究所   362000）