基于三维点云的铸件飞边打磨点提取及拟合方法*

周海陶，陈新度，吴 磊

（广东工业大学机电工程学院，广州 510006）

0 引言

目前，我国铸件产量不断增加，利用传统人工打磨铸件飞边具有打磨效率低、打磨质量不稳定、人工成本高、打磨粉尘大，影响工人健康等缺点[1]。自动化技术具有低成本、高效率等特点[2]。因此，将机器人等自动化智能设备运用到铸件打磨领域具有巨大的发展前景[3]。

现有的机器人打磨方法主要是基于铸件CAD 模型，在模型中获取相应的打磨路径，利用CAM 软件规划该路径，但是，大部分商用的CAM软件都是基于机床的CAM进行改进的，将其直接运用到机器人可能会造成运动限制问题[4]。同时，由于铸造技术的限制，现实铸件与CAD 模型之间存在铸造余量，无法准确提取现实铸件中待打磨部分，从而无法满足相关加工要求。席文明、谢剑阳等[5]基于铸件CAD 模型，利用机器人作为测量工具，建立CAM 空间与作业空间的映射一致性，可以提高打磨精度，但是该方法较为复杂。

针对上述情况，本文利用扫描真实工件获取的点云数据作为离线编程的模型，可以避免采用CAD 模型与实际铸件尺寸相差较大的问题，从而避免出现机器人欠打磨或过打磨的情况。其次，现有的商用CAM 软件难以处理点云数据，无法对打磨路径进行准确地控制。因此，本文提出基于铸件点云对飞边打磨点进行提取和打磨路径拟合的方法，并对路径拟合效果进行评价，拟合结果可以作为机器人打磨路径的参考。

1 总体方案

总体方案流程如图1所示。将铸件点云分割成本体和飞边两大模块。对于飞边模块，利用点云边缘检测算法，但是主流的边缘检测算法并不能很好地区分出飞边的内外边缘，由于飞边形态各异，内外边缘普遍存在高度差，而外边缘会影响机器人打磨飞边高度位置的确定。本文提出在利用法线估计边缘检测的基础上加入近邻点搜索算法，利用飞边内边缘是飞边和铸件本体界限这一特征，可以有效地区分出飞边的内外边缘。

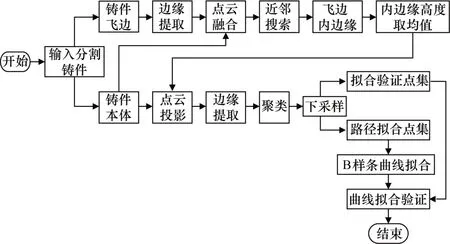
图1 总体方案流程

对于铸件本体模块，利用飞边内边缘的平均高度进行点云单侧面投影，将三维点云转换成平面点云，再提取整体边缘，但是，单纯的边缘提取会引入内腔轮廓，影响后续打磨路径的拟合。因此，本文提出在边缘提取的基础上，加入DBSCAN(Density-Based Spatial Clustering of Application with Noise)聚类算法，可以有效排除铸件的内腔轮廓，保留外层边缘。

对于打磨路径拟合，利用体素下采样算法将本体外层边缘点分为拟合点集和拟合评价点集，利用非均匀三次B 样条进行路径拟合，拟合效果利用评价点集在拟合曲线上与最近邻点的平均距离和均方根误差进行评价。

2 铸件飞边打磨点提取

2.1 飞边内边缘

铸件完整点云如图2所示；分割后的铸件本体点云如图3所示；铸件飞边点云如图4所示。

图2 铸件扫描点云

图3 铸件本体点云

图4 铸件飞边点云

利用基于法线估计对飞边点云进行边界检测，实际上近似于估计点云表面的相切面法线的问题[6]。待拟合的平面方程如下所示：

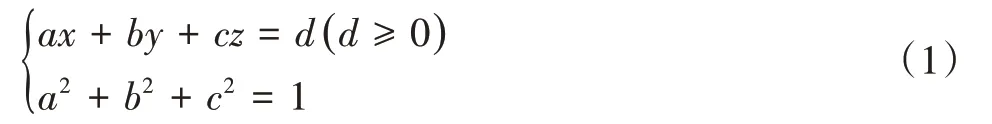
估计点到拟合平面的距离为：

要得到最佳的拟合平面，可转化成求解极值问题，如下所示：

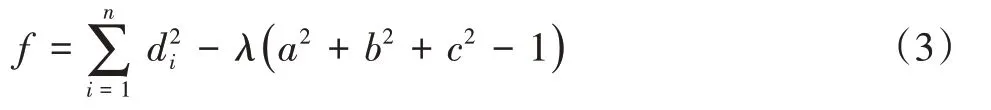
将式（3）对d求偏导，并化简，得到：

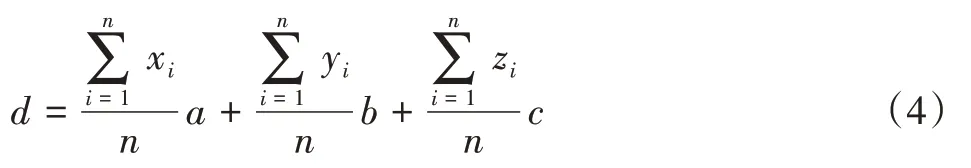
将式（4）代入到式（2）可得：

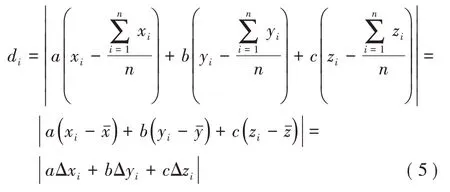
式（3）继续对a、b、c求偏导，可得：

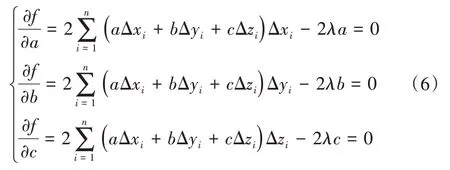
将式（6）中统一得：

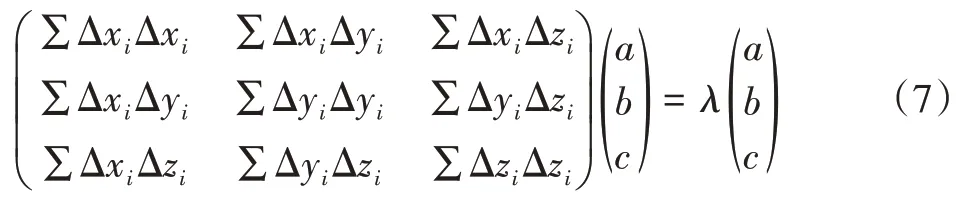
根据式（7）求解出的最小特征值对应的特征向量即为所选点云的法向量。

利用各个法线方向之间夹角的大小判断所求的点是否为边界点，对相邻的夹角顺时针两两做差得到Ω=(θ1,θ2,θ3,…,θ1)，找寻Ω中最大的夹角θmax，若θmax大于阈值，则选定的目标点为边界点，否则为非边界点。铸件飞边的边缘提取如图5所示。

图5 铸件飞边边缘

点云边缘检测算法只能提取出飞边的边界点，无法区分飞边的内外边缘。现实中飞边的内外边缘往往存在高度差，飞边的内边缘紧邻铸件的本体，因此内边缘可以确定铸件的打磨位置，引入外边缘反而会使打磨位置有较大的误差。故本文在边缘提取的基础上，加入在铸件本体区域近邻点搜索算法，利用飞边的内边缘是铸件本体和飞边的界限这一特征，在指定点半径范围内搜索到的铸件本体的点数大于阈值k，则该指定点为飞边的内边缘点，从而可以区分出飞边的内外边缘，提取完整的内边缘。飞边的内边缘如图6所示。

图6 铸件飞边内边缘

2.2 打磨路径拟合点

将所得飞边内边缘的高度取平均值，该高度值作为铸件打磨位置的高度。铸件本体按照该高度的平面进行单侧面的点云投影，将三维点云转化为平面点云。点云的投影结果如图7所示。

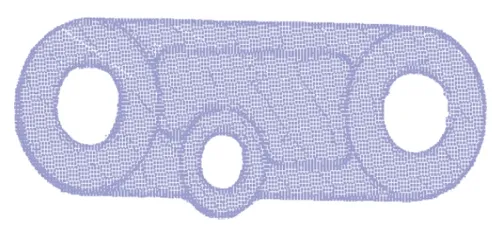
图7 铸件本体单侧面投影

得到铸件本体的平面点云后，利用边缘检测算法提取该点云的轮廓。铸件本体的内腔轮廓和外层轮廓如图8所示。对铸件本体的平面点云采用边缘检测算法会引入铸件的内腔轮廓。故本文在边缘检测的基础上加入DBSCAN 聚类算法，目的是排除铸件本体的内腔轮廓，保留外层边缘。DBSCAN 聚类算法是一种基于密度的聚类算法，可以在非凸集合上获得很好的聚类效果[7]。样本点集为D=(x1,x2,…,xm)，样本点的∊邻域定义如下：

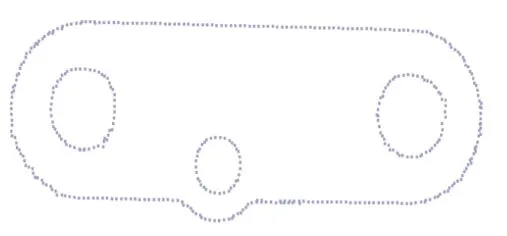
图8 铸件本体轮廓和内腔轮廓

样本点X(i)∊邻域的样本个数Nξ(X(i))如下：

通过与设定的密度下限minPts 可以将样本点分为核心点、边界点和噪声点3 大类[8]。核心点为样本点X(i)处的密度高于minPts；边界点为样本点X(i)处的密度小于minPts，但该样本点在某一核心点的邻域内；噪声点既不是核心点也不是边界点。通过寻找一系列的高密度的核心点，以及核心点外层的边界点，将样本点聚类成簇。通过聚类可以将样本点分成不同的样本点类，从而可以对不同的样本点类进行不同的操作。排除内腔轮廓的铸件本体的外层边缘如图9所示。

图9 铸件本体外层边缘

由于提取的铸件本体外层边缘的点数较多，密度较大，不适合直接进行拟合操作。故本文对提取的点进行体素质心下采样，选取合适的打磨路径拟合样本点。该算法首先将铸件的外层边缘进行体素划分，利用非空体素中的质心代替该体素中的边缘点，从而实现边缘点的下采样[9]。同时将下采样点分为路径拟合点集和拟合评价点集。体素的质心为：

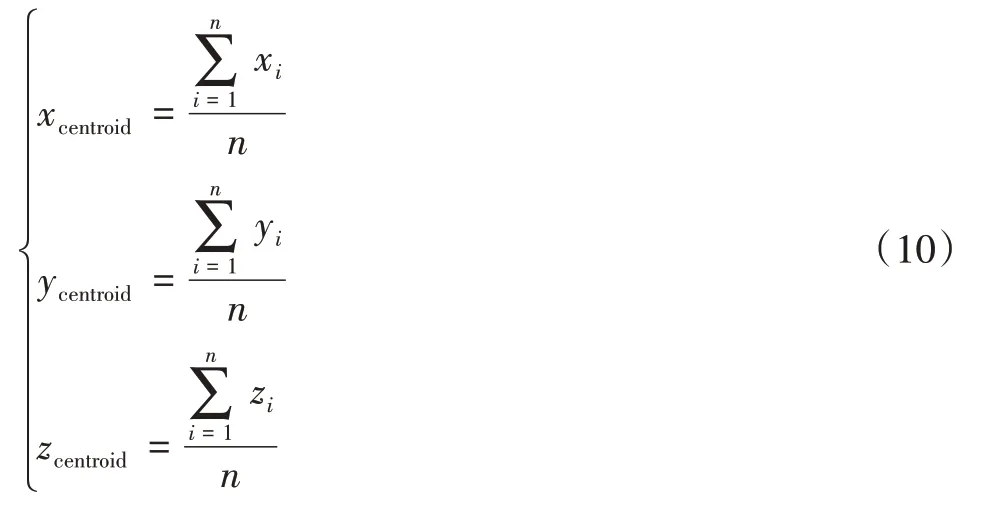
路径拟合点集如图10所示。

图10 路径拟合点集

3 打磨路径拟合

3.1 三次非均匀B样条曲线

在获取铸件本体外边缘下采样点后，需要对其进行打磨路径的拟合规划，以便机器人打磨。由于铸件的外边缘轮廓较为多样，属于自由曲线。若采用多项式曲线方法进行拟合需要高阶多项式，可能出现过拟合问题，且拟合效果受干扰点影响较大[10]。同时，多项式曲线拟合不方便后续打磨点的调整，拟合后的整体曲线会因为某个点的改变而发生变化。相比于多项式曲线拟合，利用B 样条曲线拟合可以用分段低阶多项式通过连续的连接来代替高阶多项式，可以避免过拟合的情况，同时，B 样条中的分段曲线相互独立，不同但连续的曲线段只受相应控制点的影响，因此，进行曲线拟合后还可以根据实际打磨路径需要修改某处控制点，进而带动相应的分段曲线进行改变，但是不会影响其他的曲线段，且整体的曲线拟合仍然保持连续。

非均匀有理B 样条(NURBS Non-Uniform Rational BSplines)的曲线方程表达式，有理分式如下：

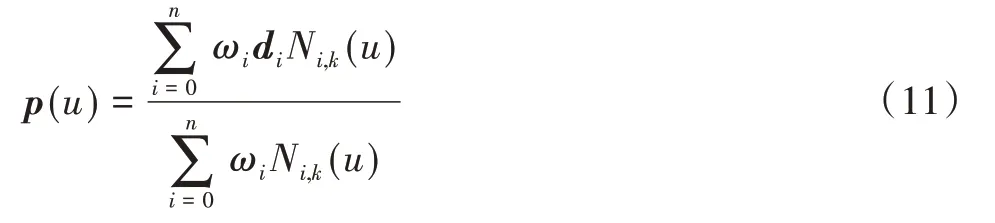
式中：

其中，ωi(i=0,1,…,n)称为权因子，ω0、ωn＞0，其余ωi≥0，且不能连续k个权因子同时为0，k为k次曲线。di(i=0,1,…,n)为曲线的控制顶点，ωi与其对应，顺序连接控制顶点可以获得控制多边形。Ni,k(u)是由节点矢量U={u0,u1,…,un+k+1} 确定的k次规范B 样条基函数，其中，首末节点的重复度r=k+1。即：

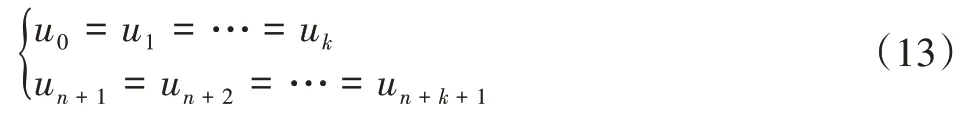
本文对打磨路径拟合采用的是非均匀三次B 样条曲线插值拟合方法，k=3。选取铸件本体外层边缘的下采样点中的92个点作为曲线的型值点，因此，需要进行曲线的反算，一般包括计算节点矢量，确定边界条件，反算曲线控制顶点3个步骤[11]。

pi点有节点值ui+k(i=0,1,…,n)。首先需要对型值点进行参数化处理，确定型值点的参数值ui+k。具有n+1 个型值点pi的三次NURBS 曲线是由n+3 个控制顶点di(i=0,1,…,n+2) 及其权因子ωi和节点矢量U={u0,u1,…,un+6} 定义，由于首末节点的重复度r=k+1，故前k+1 个节点取值为0，后k+1 个节点取值为1。考虑到数据点多边形各弦长分布不均匀的情况，本文采用积累弦长参数化法求解各型值点pi的参数值，如下所示：

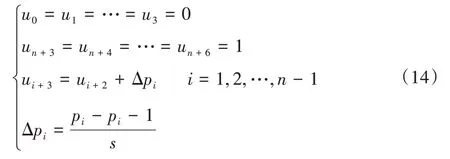
其次，确定拟合曲线的边界条件，由于本文的打磨路径为闭合曲线，即首末端点重合且二阶连续，则边界条件为：

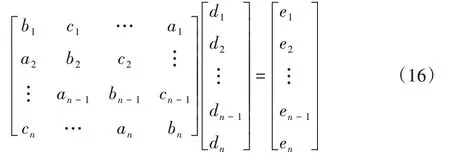
最后，求解NURBS曲线的控制顶点。对于二阶连续的NURBS三次闭合曲线，首末数据点相同，其控制顶点反算的矩阵表达式为：

其中：

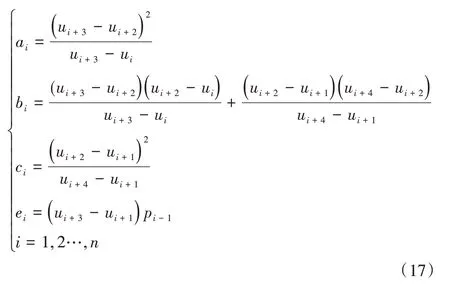
根据上述的方程式组，可以求解出NURBS曲线的控制顶点，结合求得的节点矢量和曲线边界条件，根据要求选择合适的权因子，本文的权因子wi(i=0,1,…,n+2)取值为1，最终可以确定三次非均匀NURBS 曲线。本文的打磨路径插值拟合效果如图11所示。图中，圆型点为提供拟合插值的型值点；星型点为NURBS曲线反求的控制顶点；折线为顺序连接控制顶点形成的曲线控制多边形；粗曲线为拟合的打磨路径。

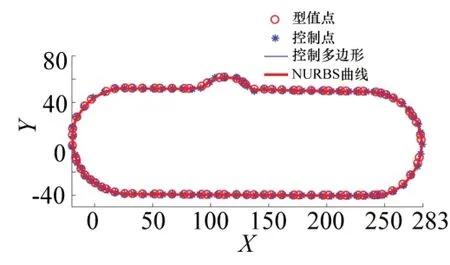
图11 打磨路径拟合

3.2 曲线拟合评价

利用非拟合点作为评价点集对打磨路径的拟合效果进行评价。评价点作为目标点，拟合后的曲线作为搜索区域，计算目标点与最近邻点的距离，利用其平均距离和均方根误差对NURBS曲线进行评价。如下所示：

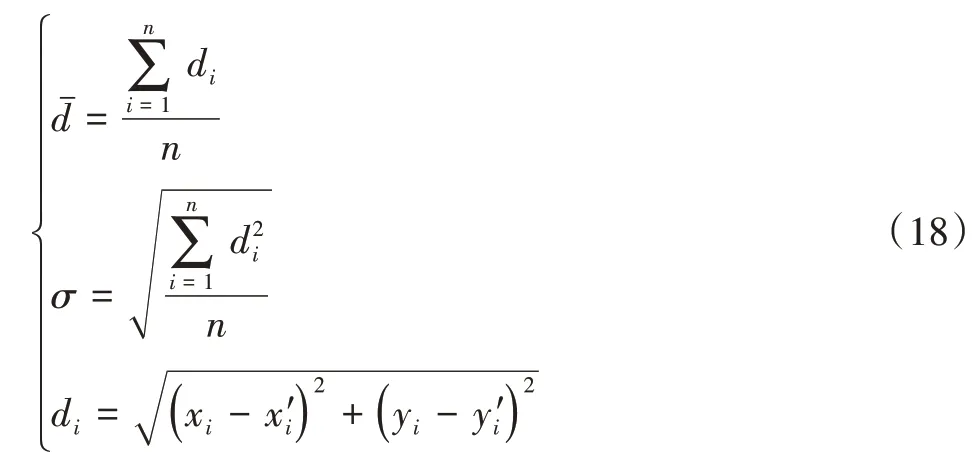
式中：(xi,yi)和(x＇i,y＇i)分别为评价点集和对应最近邻点的坐标。

根据上式所得，评价点与曲线的最近邻点平均距离为0.174 812 mm，其均方根误差为0.249 56。因为本文针对的铸件飞边打磨为粗加工，故曲线拟合效果符合粗加工要求。图12所示为评价点集和对应的最近邻点。

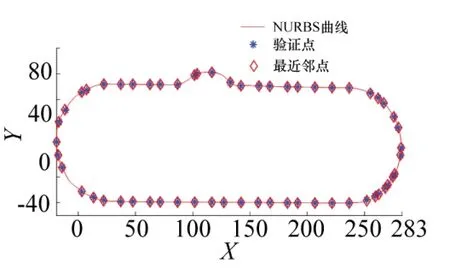
图12 评价点集和最近邻点

4 结束语

本文基于真实铸件的点云信息，提出一种对铸件飞边打磨点提取和路径拟合的方法。该方法提出利用点云的基于法线估计边缘检测和近邻点搜索结合的方法区分飞边的内外边缘，避免外边缘对打磨位置造成干扰；利用单侧面投影和DBSCAN 聚类结合的方法去除铸件的内腔轮廓，保留外层边缘，减少后续打磨路径拟合的干扰；利用体素下采样提取铸件飞边的打磨点，运用三次非均匀有理B 样条曲线插值拟合算法对打磨路径进行拟合，通过评价点集对拟合效果进行评价，评价点集与曲线的最近邻点的平均距离和均方根误差为0.174 812 mm 和0.249 56，反映曲线拟合误差较小，可以作为铸件边缘粗加工的路径参考。