Measurement-device-independent one-step quantum secure direct communication

Jia-Wei Ying(应佳伟) Lan Zhou(周澜) Wei Zhong(钟伟) and Yu-Bo Sheng(盛宇波)

1College of Electronic and Optical Engineering&College of Flexible Electronics(Future Technology),Nanjing University of Posts and Telecommunications,Nanjing 210023,China

2Institute of Quantum Information and Technology,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

3College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China

Keywords: measurement-device-independent, one-step quantum secure direct communication, hyperentanglement Bell state measurement, hyperentanglement-assisted complete polarization Bell state measurement

1. Introduction

In the 21st century, the information security has been widely concerned. Quantum communication based on the basic principle of quantum mechanics can provide an absolute security guarantee of the communication. Quantum communication began as the research on quantum key distribution(QKD).[1–3]QKD can distribute secure keys between two distant parties, which was first proposed in 1984.[1]Combined with extra one-time pad and the one-way classical communication, the communication parties can realize the secure communication. During past decades, QKD has made great progress in both theory[4–14]and experiment.[15–23]For example,in the theory aspect,the device-independent(DI)QKD[4]and measurement-device-independent (MDI) QKD can efficiently enhance QKD’s security under practical imperfect experimental condition.[4–9]The twin-field(TF)QKD improves the key rate-transmittance bound from linear to square root.[14]In the experimental aspect, Yinet al.in 2020 built a timephase encoding system to implement the four-intensity decoystate BB84 QKD protocol.[15]In 2021,Chenet al.realized the space-to-ground quantum communication network over 4600 km.[16]Recently, the chip-based QKD[18]and TF-QKD experiment over an 830-km fibre[23]were also reported. Besides QKD, there appears to be some important branches of quantum communication, such as quantum teleportation(QT),[24–28]quantum secret sharing (QSS),[29–33]and quantum secure direct communication.[34–54]QT enables a communication party to send the encoded messages to a remote party without sending the encoded particle itself. In QSS, a dealer can distribute the keys to multiple participants. All the participants can obtain the keys only by cooperation.

Quantum secure direct communication (QSDC) which will be detailed here is a new quantum secure communication mode. It can directly transmit secure messages between two communication parties without keys. Meanwhile,QSDC can also realize the task of QKD. The first QSDC protocol known as the efficient QSDC protocol was proposed by Long and Liu in 2000.[34]In 2003 and 2004,the typical twostep QSDC protocol based on Einstein–Podolsky–Rosen pairs and the QSDC protocol based on single photons (DL04 protocol) were successively proposed.[35,36]In 2005, Wanget al.proposed the QSDC protocol with high-dimension quantum superdense coding.[37]The DL04 protocol and two-step QSDC protocol were experimentally demonstrated in 2016 and 2017, respectively.[38,39]In recent few years, QSDC has developed rapidly in both theory and experiment.[40–54]In theory,DI-QSDC and MDI-QSDC were put forward,which can largely enhance QSDC’s security under practical experimental condition.[41–44]In 2021,Long and Zhang adopted the masking technology in QSDC to increase its capacity,communication distance,and tolerable error rate greatly.[49]In the experimental aspect, a 15-user QSDC network with any two users being 40 km apart was realized in 2021.[51]Later,researchers achieved the QSDC over a 100-km fiber with time-bin and phase quantum states.[53]

In 2021, the one-step QSDC[52]based on polarizationspatial-mode-hyperentanglement was proposed, where the communication parties only require to transmit photons in the quantum channel once to construct the hyperentanglement channel. Then, the message sender encodes his messages in the polarization degree of freedom(DOF)and the parties perform the nonlocal complete polarization Bell state measurement (BSM) assisted by the spatial-mode entanglement.[55]The message receiver can read out the encoded messages according to the BSM results. The one-step QSDC can effectively simplify QSDC’s operation and reduce message loss.However, similar to previous QSDC protocols, the one-step QSDC requires perfect and trusted experimental devices. For enhancing its security in practical imperfect experimental condition, in this paper, we propose two MDI one-step QSDC protocols, which can resist all possible attacks from practical imperfect measurement devices. In both MDI one-step QSDC protocols,the communication parties are only responsible for preparing polarization-spatial-mode hyperentanglement and hyper-encoded single photons and for encoding. All the measurement tasks are handed over to the third party. The parties first construct the hyperentanglement channel by the hyperentanglement swapping method. In the first MDI onestep QSDC protocol, we adopt the complete hyperentanglement Bell state measurement (HBSM) with the help of the cross-Kerr nonlinearity,while in the second protocol,we adopt the feasible linear-optical partial HBSM. Then, the message sender encodes his messages in the polarization DOF of his remaining photons and the receiver randomly encodes his photons. As they cannot measure the photons, they should send the encoded photons to the measurement party for the complete polarization BSM assisted by the spatial-mode entanglement. Then,the receiver can finally read out the encoded messages according to the BSM results and his own encodings.Our two MDI one-step QSDC protocols have potential applications in the future quantum secure communication field.

The structure of this paper is organized as follows. In Section 2, we explain our first MDI one-step QSDC protocol. In Section 3,we briefly explain the second MDI one-step QSDC protocol and analyze the influence from the adoption of linear-optical partial HBSM on its message transmission and security. In Section 4, we analyze the security of our MDI one-step QSDC protocols.In Section 5,we simulate the secret message capacity of the first MDI one-step QSDC protocol.In Section 6,we make some discussion and conclusion.

2. The MDI one-step QSDC protocol with the nonlinear complete HBSM

In this section,we explain our MDI one-step QSDC protocol with the complete HBSM.As shown in Fig.1,there are three parties in our protocol. Alice (A) and Bob (B) are the message sender and receiver, respectively. Charlie (C) is an untrusted third party,who can even be controlled by the eavesdropper (Eve). The whole protocol can be described as follows.

Fig.1. Illustration of the first MDI one-step QSDC protocol. A,B,C stand for Alice, Bob, and Charlie, respectively. The pattern of yellow and blue balls represents the initial hyperentangled state〉prepared by Alice and Bob. The pattern of two blue balls represents the hyper-encoded single photon. The solid and dashed lines represent the initial and the constructed hyperentanglement,respectively.

Step 1: Alice and Bob both preparen(nis large)identical polarization-spatial-mode hyperentangled photon pairs in|Ψ〉=|ψ+P〉⊗|ψ+S〉. Alice(Bob)takes one photon from each hyperentangled photon pair to form an ordered photon sequenceSA(SB) and takes the other photons to form the ordered photon sequenceCA(CB).Then,Alice(Bob)preparesmpolarization-spatial-mode hyper-encoded single photons and inserts them randomly into the sequenceCA(CB). In this way,there arenphotons in sequenceSA(SB) andn+mphotons in sequenceCA(CB). The single photons are randomly prepared in the rectilinear basisZP(ZS) and diagonal basisXP(XS)in the polarization(spatial-mode)DOF.ZPandXPcan be described as

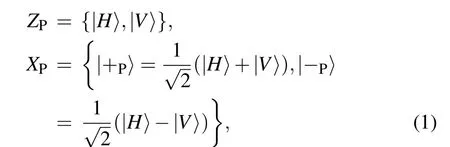
where|H〉and|V〉represent the horizontal and vertical polarization,respectively.ZSandXSin Alice’s and Bob’s locations can be respectively written as

Step 2: Alice and Bob send the photons in sequencesCAandCBto the third party Charlie. After Charlie receiving the photons,he performs the complete HBSM with the help of the cross-Kerr nonlinearity[56]on each photon pair.

Step 3:Charlie announces the HBSM result for each photon pair. Alice and Bob announce the positions and quantum states of the hyper-encoded photons. If one photon for the HBSM is the hyper-encoded single photon and the other one is from the hyperentangled photon pair, Alice and Bob will discard the HBSM result and the corresponding photon inSAorSBsequence. If both photons for the HBSM are from the hyperentangled photon pairs,after the HBSM,the corresponding remained photons inSAandSBsequences can construct the hyperentanglement channel with the hyperentanglement swapping. In detail, the whole photon state can be written as

For example, if the HBSM result is|ψ+P〉⊗|ψ−S〉CACB, the hyperentangled state between Alice and Bob is|ψ+P〉SASB⊗|ψ−S〉SASB.The constructed hyperentangled states in sequencesSAandSBare known to all.

If both photons for the HBSM are hyper-encoded photons,the HBSM results can be used for security checking. As shown in Ref. [7], there are two possible cases. First, if the two single photons are generated with different bases in both DOFs,the HBSM results and the encodings in both DOFs cannot be used for security checking. For example, for the photon pair in|H〉|a′1〉⊗|+P〉|+S〉B, the whole photon state will evolve to

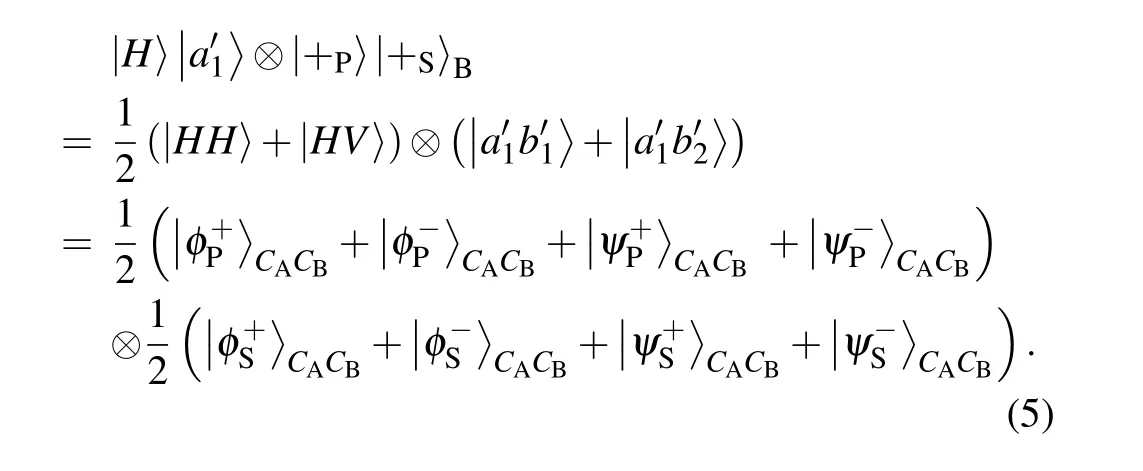
It can be found that the HBSM result may obtain all the sixteen hyperentangled Bell states with the same probability and the parties cannot detect whether an error occurs in each DOF.As a result, the parties have to discard the HBSM results and the encodings in both DOFs.

Table 1. Possible BSM results and corresponding probability in the polarization DOF.

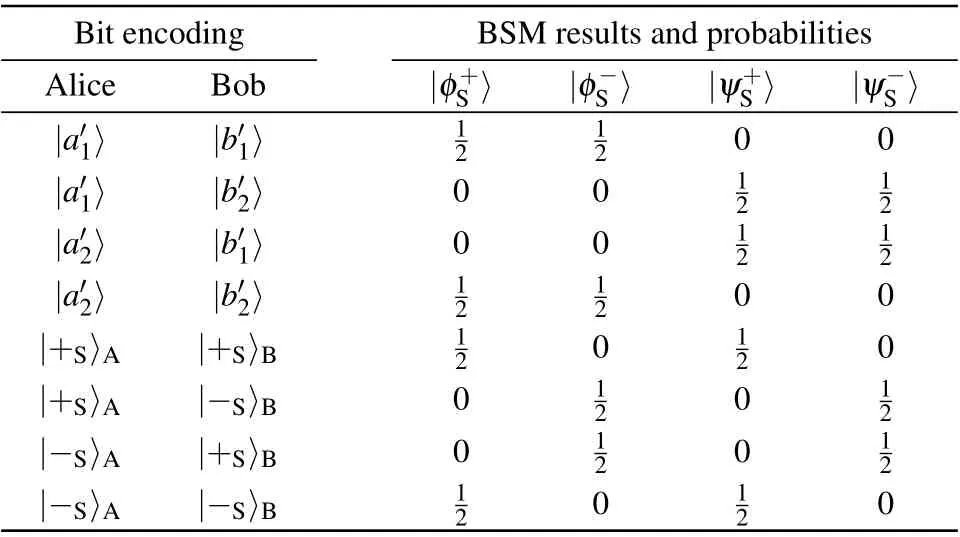
Table 2. Possible BSM results and the corresponding probability in the spatial-mode DOF.

Second, if the two single photons are generated with the same basis in a DOF,the BSM results and the encodings in this DOF can be used for security checking. The possible BSM results and the corresponding success probability in the polarization DOF and spatial-mode DOF are listed in Table 1 and Table 2,respectively. For example,for the quantum state|H〉|a′1〉⊗|+P〉|b′2〉or|H〉|a′1〉⊗|H〉|b′1〉,the photon state can be written as

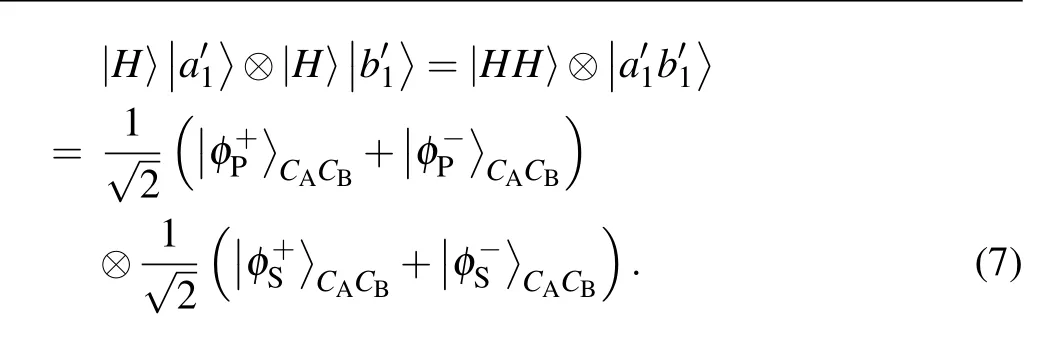
It can be found that when the two photons have the same basis in a DOF, the BSM result in this DOF only has two possible Bell states. If Charlie obtains the other result, the parties can ensure that an error occurs in this DOF.As a result,when the photons have the same basis in a DOF,the BSM result in this DOF can be used for security checking. After the security checking,the parties estimate the bit error rate in both DOFs.If the bit error rate in any DOF exceeds a certain threshold,the photon transmission is unsafe and the parties have to discard the communication. Otherwise,they will ensure that the photon transmission is secure and go to the next step.

Step 4: Alice performs one of the four unitary operations on the photons inSAsequence to encode her messages in the polarization DOF. The four unitary operations have the form of

whereU0,U1,U2,andU3represent four classical messages 00,01,10,and 11,respectively. Meanwhile,she randomly selects some photon pairs as the second round of security checking photon pairs and performs random operations on them. In order to prevent message leakage,Bob also randomly performs one of the above four unitary operations on all the photons inSBsequence. We call the encoded photon sequences asMAandMB,respectively.

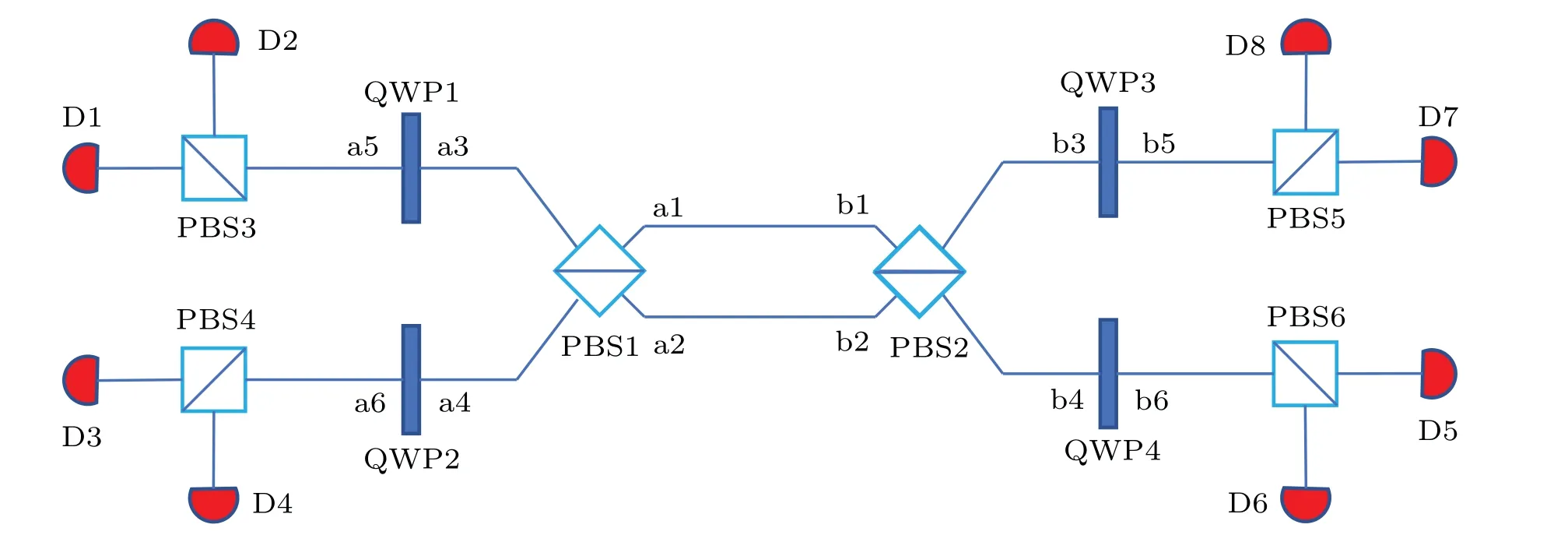
Fig. 2. The basic principle of the complete polarization BSM assisted by spatial-mode entanglement. Here, PBS represents the polarization beamsplitter,whichcan totally transmit thephotonin |H〉andtotally reflectthe photon in|V〉.QWPmeansthequarter wave plate, which makes|H〉→(|H〉+|V〉)and|V〉→(|H〉−|V〉). Di(i=1,2,...,8)representsthe singlephotondetector.

Table 3. The polarization Bell states corresponding to the detector responses with different spatial-mode entangled states.

Step 5: Alice and Bob send the photons in sequencesMAandMBto Charlie. After receiving the photons, Charlie performs the complete polarization BSM assisted by the spatial entanglement on each photon pair.[2]The basic principle of such BSM is shown in Fig. 2. The polarization Bell states corresponding to the detector responses with different spatialmode entangled states are shown in Table 3. In this way, according to the detector responses,Charlie can completely distinguish four polarization Bell states in Eq.(3).

Step 6: Charlie announces his BSM results and Alice announces the positions and operations on the security checking photon pairs. For the message transmission photon pairs,Bob can deduce Alice’s coding operation combining the BSM result with his own random operation, thus can finally read out the encoded message. For the security checking photon pairs,Bob can estimate the error rate. If the bit error rate exceeds a certain threshold,the photon transmission is unsafe and the parties have to discard the communication and the transmitted messages. Otherwise,if the bit error rate is lower than the threshold, they ensure that the photon transmission is secure and keep the transmitted messages.

3. The second MDI one-step QSDC protocol with the linear-optical partial HBSM

For enhancing the practicability of the MDI one-step QSDC protocol,we propose the second MDI one-step QSDC protocol,which adopts the linear-optical partial HBSM protocol in Ref.[57]in step 2.The linear-optical partial HBSM protocol can distinguish 12 of the 16 hyperentangled Bell states assisted by the time-bin DOF. The distinguishable 12 hyperentangled states are|φ±P〉⊗|φ±S〉,|ψ±P〉⊗|ψ±S〉, and|ψ±P〉⊗|φ±S〉. For the other 4 hyperentangled Bell states|φ±P〉⊗|ψ±S〉,this HBSM protocol can only distinguish|ψ±S〉but cannot distinguish|φ±P〉.[57]This partial HBSM protocol only requires linear-optical elements, and is feasible with current experimental technology.

Then,we analyze the influence from adopting the linearoptical partial HBSM protocol on the security and communication efficiency of our MDI one-step QSDC. If the HBSM obtains one of the four hyperentangled states|φ±P〉⊗|ψ±S〉,the situation that the partial HBSM cannot distinguish|φ±P〉would influence the security checking and the construction of hyperentanglement channel. As shown in Table 1, during the security checking process of step 3,if both parties use the rectilinear basis,|φ±P〉both correspond to the even parity|H〉|H〉and|V〉|V〉. In this case,the situation that Charlie cannot distinguish|φ±P〉will not cause error in the polarization DOF,so that the encoded bits and the BSM result in the polarization DOF can still be used in the security checking. On the other hand,if both parties use the diagonal basis,|φ+P〉corresponds to the even parity|+P〉|+P〉and|−P〉−P〉, while|φ−P〉corresponds to the odd parity|+P〉|−P〉and|−P〉|+P〉. As a result,if Charlie randomly announces|φ+P〉or|φ−P〉,it may cause error in the polarization DOF.As a result,for avoiding the error caused by the partial HBSM,the parties have to discard the encoded bits and the BSM result in the polarization DOF when Charlie obtains|φ±P〉⊗|ψ±S〉,but only use the BSM result and the encoding bits in the spatial-mode DOF to check the security. On the other hand, in the hyperentanglement swapping process, if Charlie obtains|φ±P〉⊗|ψ±S〉, the communication parties cannot determine the constructed quantum state in the polarization DOF, which may make Bob obtain wrong messages by comparing the constructed quantum state and encoded quantum state in the polarization DOF.For avoiding the message error, the parties have to discard the corresponding hyperentangled photons inSAandSBsequences. As Charlie may obtain|φ±P〉⊗|ψ±S〉with the probability of 1/4,Alice can transmit 1.5 bits of classical messages to Bob in each communication round in statistics.

4. Security analysis

Now,we analyze the security of our MDI one-step QSDC protocols in theory.In the protocols,all the measurement tasks are handed over to the third measurement party Charlie, who can be even controlled by Eve and the measurement results are public to all. We show the relationship among the first HBSM result in the polarization DOF,the complete polarization BSM result and Alice’s and Bob’s joint operations in Table 4. We set the HBSM result in the polarization DOF as|ψ+〉for simplicity. If the HBSM obtains the other result, we can obtain the similar results. From Table 4, the BSM result is independent of Alice’s bit value. One can read out Alice’s encoded message only by combining the BSM result with Bob’s operation. As Bob’s random operation is private,only Bob can obtain the encoded messages. Meanwhile,if Charlie deliberately announces wrong HBSM or BSM result, Bob may read out wrong messages according to the measurement results. However, as Charlie does not know the positions of the security checking photons before announcing the measurement results,his dishonest behavior may increase the error rate. In this way,his dishonest behavior can be detected by the communication parties.Based on the above analysis,our protocol can resist all the possible attacks from the imperfect measurement devices and the measurement party.

Table 4. The relationship among the HBSM result in the polarization DOF, the complete polarization BSM result and Alice’s and Bob’s joint operation. Here,we set the HBSM result in the polarization DOF as|ψ+〉for simplicity.

Then, we consider a common attack mode, say, the intercept-resend attack. For achieving the goal of MDI, the parties require to transmit photons in quantum channels twice.During the first photon transmission process,Eve can intercept some photons from Alice. For avoiding detection,he prepares some single photons and sends them to Charlie to make the HBSM.In this way,Alice actually constructs the hyperentangled channel with Eve.During the second photon transmission process,Eve also intercepts the corresponding photons of the intercepted photons in the first photon transmission, so that he can finally obtain Alice’s encoded messages by performing the polarization BSM.In the protocol,the communication security is guaranteed by two rounds of security checking. During the first photon transmission process,as the randomly encoded security checking photons are randomly inserted into theCAandCBsequences,Eve may steal some security checking photons inevitably. As Eve does not know the generation basis of the single photons, he can only randomly chooseZorXbasis to measure the photons in both DOFs and generate a new photon according to his measurement result. When Eve chooses wrong basis,his new generated photon may cause wrong HBSM result and increase the error rate,so that the parties can detect Eve’s attack. As long as the security of the first photon transmission process can be guaranteed, Eve cannot steal meaningful messages even if she could steal some photons during the second photon transmission process. Meanwhile,Charlie(Eve)cannot obtain the encoded messages from the HBSM and polarization BSM results,because he does not know Bob’s random encoding in the polarization DOF.However, the intercept-resend attack in the second photon transmission process would make Charlie obtain wrong BSM results and disturb the communication. We set the second security checking to guarantee the security of the second photon transmission process. As a result, with the help of two rounds of security checking, the security and correctness of the messages can be guaranteed. Our protocols can resist the intercept-resend attack in theory.

Third, we consider another common attack, the Trojan horse attack,in which the attacker inserts his own photons into the photon sequences to steal the encoded messages. In our protocol,with the help of the entanglement swapping,the photons to be encoded are always in Alice’s and Bob’s locations before the encoding. In this way,the eavesdropper cannot insert photons into these photon sequences to steal the encoded messages,so that our protocols can also resist the Trojan horse attack.

5. Simulation of the MDI one-step QSDC protocol’s secrete message capacity

Taking Eq.(14)into Eq.(11),we can finally calculate the value ofCs.

In Fig.3,we provide the value of logCsper pulse altered with the photon transmission distancedfrom Charlie to Alice(Bob). It can be found that with the complete HBSM and linear optical complete polarization BSM, the maximal photon transmission distance can reach about 177 km,so that the maximal communication distance is about 354 km.

Fig. 3. The secrete message capacity (logCs) per pulse altered with the photon transmission distance d from Charlie to Alice(Bob). Here,we suppose that Alice and Bob use the SPDC sources to generate hyperentangled states with p′ =10−3. During each photon transmission process, we set the misalignment error rates in both DOFs as emP =emS=1.5%. We also set the inherent efficiencies as ηl1=ηl2=98%,the error rate of the homodyne measurement as ed=1%,the single photon detector in the complete polarization BSM process is 90%efficient with the dark-ground count rate as Y0=6.02×10−6.

6. Discussion and conclusion

In this paper, we propose two MDI one-step QSDC protocols based on the polarization-spatial-mode hyperentanglement. In our protocols, both Alice and Bob require photon state generation and the encoding. All the measurement tasks are handed over to the third party Charlie. In this way, our protocols can resist all possible attacks from practical imperfect measurement devices. In both protocols,with the help of the HBSM,Alice and Bob can construct the deterministic hyperentanglement channel by the hyperentanglement swapping.Then,after Alice’s and Bob’s encoding,they send the encoded photons to Charlie for the complete polarization BSM assisted by the spatial-mode entanglement. Bob can finally read out Alice’s encoding messages based on Charlie’s measurement results and his own encoding. In the first protocol, with the help of the complete HBSM, Alice can transmit two bits of messages to Bob by consuming two pairs of hyperentangled states. In the second MDI one-step QSDC protocol, with the practical partial HBSM, Alice can transmit 1.5 bits of messages to Bob by consuming two pairs of hyperentangled states in statistics.

Here, the HBSM is the key element of our protocols.With the complete HBSM,our first MDI one-step protocol can achieve the higher capacity. Besides the HBSM in Ref. [56],there are other complete HBSM protocols with nonlinear optical elements, such as the cross-Kerr nonlinearity and artificial atoms.[65–68]The nonlinear optical elements have gained great progress in recent years.[69–73]In 2016, Becket al.obtained a large conditional cross-phase shift ofπ/6 between signal fields stored in an atomic quantum memory.[70]Soon later, Tiarkset al.reported the strong interactions in Rydberg electromagnetically induced transparency (EIT) experiments, which can create a large controlled phase shift of 3.3±0.2 rad, with the control pulses containing an average of 0.6 photons.[72]In 2020, Sinclairet al.reported the cross-Kerr nonlinearity in a free-space medium based on the Rydberg atoms and EIT technology. They obtained the nonlinear phases as 8 mrad/nW of signal power,corresponding to aχ3of 10−8m2/V2.[73]In this way, with the experimental development of the nonlinear optical elements,it is possible to realize the complete BSM in the near future.

In conclusion, for enhancing one-step QSDC’s security under practical experimental condition,we propose two MDI one-step QSDC protocols,which can resist all possible attacks from the imperfect measurement device. In the MDI onestep QSDC protocols, Alice and Bob prepare a large number of identical polarization-spatial-mode two-photon hyperentangled states. Then, they send one photon of each hyperentangled photon pair to the third party Charlie to make the HBSM.In this way, Alice and Bob can construct the hyperentanglement channel with the hyperentanglement swapping. The first MDI one-step QSDC protocol uses the nonlinear complete HBSM to construct the hyperentanglement channel,while the second protocol uses the linear-optical partial HBSM. Then,Alice encodes her messages on her remaining photons in the polarization DOF by performing unitary operations and Bob also randomly operates his remaining photons to prevent message leakage. After encodings,Alice and Bob send their photons to Charlie. Charlie performs the linear-optical complete polarization BSM assisted by the spatial-mode entanglement on each photon pair and announces his measurement results.Combining Charlie’s measurement results with his own random operations, Bob can finally deduce Alice’s messages.Both the MDI one-step QSDC protocols are unconditionally secure in theory. In the first MDI one-step QSDC protocol,Alice can transmit 2 bits of message to Bob by using two hyperentangled photon pairs. In the second protocol, with the feasible linear-optical partial HBSM, Alice can transmit 1.5 bits of message to Bob by using two hyperentangled photon pairs in statistics. Our one-step MDI-QSDC protocols, especially the second protocol,may have potential applications in the near future.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 11974189 and 12175106), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China(Grant No.20KJB140001),and the Postgraduate Research&Practice Innovation Program of Jiangsu Province,China(Grand No.KYCX22-0963).