基于Sinkhorn距离特征缩放的多约束非负矩阵分解算法

李松涛 李维刚* 甘 平 蒋 林

①(武汉科技大学冶金自动化与检测技术教育部工程研究中心 武汉 430081)

②(武汉科技大学冶金装备及其控制教育部重点实验室 武汉 430081)

1 引言

近年来，随着电子信息技术的发展，图像数据在维度与数量上双重爆发式增长，导致视觉特征与高层语义之间“语义鸿沟”逐渐增大，成为视觉感知领域的瓶颈，因此如何从图像中提取有效的低维数据来提高视觉感知的性能成为一个重要的问题[1–3]。作为一种著名的子空间学习方法，非负矩阵分解(Nonnegative Matrix Factorization, NMF)可以以适当的方式在低维子空间中表达高维数据，进而可以更好地揭示数据的潜在结构信息，并提高各种模式感知算法的能力[4]。由于NMF算法的非负性子空间表达更符合人们心理学和生理学对整体数据感知的描述，而且其对整体数据的分解符合纯加性的感知，这也更易于直观的理解，因此它在某种意义上抓住了数据描述的本质，这与其他子空间学习方法(例如矢量量化(Vector Quantization, VQ)、主成分分析(Principal Component Analysis, PCA)、奇异值分解(Singular Value Decomposition, SVD)等)相区别。NMF在多种任务中取得了令人印象深刻的性能，例如社区检测[5]、高光谱解混[6]、面部特征提取[7]、推荐系统[8]等。

传统NMF算法的缺点之一是忽略了数据集的固有结构，该问题表现在多个方面。首先，样本之间的相关性可能存在于原始数据集中，所以希望可以利用这些相关性信息来提高NMF的性能；其次，特征之间存在一定的相关性，基于高斯误差的L2距离方法不能准确度量特征之间的距离，这使得样本内部特征的相关性较弱，导致NMF算法对高维空间的平移噪声有着不准确的预估，抑制了算法的性能；最后，原NMF算法在分解过程由于其非负性的约束条件，忽略了编码矩阵的稀疏性约束，导致分解结果的稀疏性较低，进而影响全局的稀疏表达。

为了克服上述限制，研究人员主要从两个方面着手优化研究，多数研究围绕算法本身改进展开，如Shirdhonkar等人[9]使用地球真实距离(Earth Mover's Distance, EMD)来测量原始数据矩阵与乘积矩阵之间的差异，从而提出了EMD NMF。由于EMD对不同维度之间的关系敏感，与其他测量方法相比，EMD在感知空间差异上更加准确，因此EMD NMF能提高样本的子空间区分能力；Cai等人[10]结合流形学习的图结构理论提出了GNMF(Graph regularized Nonnegative Matrix Factorization)算法，其使用最近邻图对局部模型进行几何结构建模，旨在找到保留图结构的矩阵分解，因此GNMF保留了固有的几何结构，同时获得了隐藏语义信息的紧凑表示；Qian等人[11]结合EMD NMF与GNMF的建模思想，将Sinkhorn距离以损失函数的形式置入GNMF算法，而提出了SDNMF (Nonnegative Matrix Factorization with Sinkhorn Distance)算法，该方法在EMD NMF的基础上提高了计算速度，并保留了空间的结构与特征关联能力，有较好的子空间学习能力；Hoyer[12]提出了一种稀疏的非负矩阵分解方法(Non-negative Matrix Factorization with Sparseness constrains, SNMF)，将稀疏约束引入到NMF目标函数中，以控制分解因子的稀疏表示程度，这可以保证基于特征的零件信息表示形式的直接可解释性；Liu等人[13]提出了一种称为CNMF (Constrained Nonnegative Matrix Factorization)的半监督NMF算法，它将一些先验标签信息视为附加的硬约束，并将其集成到NMF模型中以提高区分能力。同时也有研究人员从特征选择与缩放方向入手，优化算法性能，如Li等人[14]通过K邻近算法缩放有效特征，进而放大其他非核心特征的差距，使整体数据更易被定位捕获，Jimenez-Cordero等人[15]通过同性高斯核结合特征关联方法实现特征的缩放处理，从而提出了一种高精度的支持向量机批量分类方法。

但是，这些NMF算法的变体仍然存在各种缺陷。例如，EMD NMF与SDNMF在分解过程中需要重复计算分解因子乘积与原始矩阵之间的距离，这使算法计算非常耗时，虽然SDNMF算法在计算过程中使用熵正则方法去估算整体距离而提高了计算速度，但是整体速度仍然十分缓慢；GNMF缺乏对原始矩阵特征向量之间关系的考虑，导致在处理平移噪声时性能较差；SNMF仅对分解过程施加稀疏约束，但缺乏对输入数据原始结构的约束，导致其子空间学习能力较弱；CNMF使用原始数据的标签信息，尽管提高了算法的性能，但在分解过程中未能充分利用原始数据的局部几何特征和潜在的结构信息，从而限制算法的应用范围及性能。

考虑到NMF中各种信息结构与原始特征向量之间相关性的重要性，本文提出一种基于Sinkhorn距离特征缩放的多约束非负矩阵分解算法(Semi-Supervised Sinkhorn distance sparse and dual-Graph regularized Non-negative Matrix Factorization, S3GNMF)，本算法充分利用了流形图结构、稀疏约束以及标签信息来诱导分解，同时基于Sinkhorn距离对原始特征矩阵进行缩放，提高了输入数据中的特征关联性，解决了将Sinkhorn距离引入损失函数而导致的计算效率缓慢问题，同时也提高了算法性能。在数学上，将算法公式化为定义明确的非负约束优化问题，利用KKT (Karush–Kuhn–Tucker)条件推导出交叉迭代规则。此外，通过多组算法在不同的真实数据集和平移噪声数据集上的聚类实验结果证明了所提算法的有效性。

2 基于Sinkhorn距离特征缩放的多约束非负矩阵分解

作为一种优秀的NMF变种算法，SDNMF算法通过Sinkhorn距离构造损失函数及流形图结构来保持数据的几何特征结构，提高了算法的子空间学习能力，但其缺乏考虑稀疏性与先验标签的诱导分解，因此算法整体子空间学习能力不强，同时由于反复利用Sinkhorn距离计算分解误差值，导致算法速度十分缓慢。为了克服上述问题，本文提出基于Sinkhorn距离特征缩放的多约束非负矩阵分解(S3GNMF)算法。本算法不仅首次将Sinkhorn距离作为原始矩阵的特征缩放工具，提高了特征关联性，而且将标签信息纳入双流形图结构正则化，提高了算法的子空间学习能力，同时引入稀疏约束到NMF框架中，使分解因子稀疏化并提高了算法速度，也使算法更加稳定；最后，综合上述方法建立一个集成的S3GNMF算法的目标函数，算法流程示意图如图1所示。

图1 S3GNMF算法示意图

2.1 基于Sinkhorn距离的特征缩放

给定两个离散的直方图Px与Py，距离度量矩阵M以及单位距离运输量矩阵T，EMD距离[16]定义了从Px到Py的最小运输量，该距离定义为

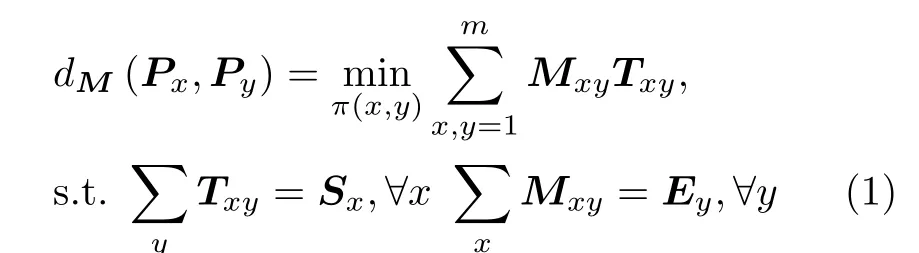
Txy表 示 由x到y的运 输 量，Mxy则 表 示x到y的 地面距离(通常以L1或L2距 离来定义) ，Sx代 表在x处需要运输的总量，Ey是y处的总运输成本。Cuturi[17]提出了一种利用熵正则化来加速EMD距离的计算方法，该方法称为Sinkhorn距离，Frogner等人[18]提出了一种将平滑传输扩展到非标准化措施的松弛方法，该方法对Sinkhorn距离中传输边缘的平等约束施加了KL散度的软惩罚，得到了一个无约束的近似运输模型，在理论上加速了Sinkhorn距离的计算。该距离方法可表示如式(2)所示

{S矩阵可以有效地实现输入矩阵的特征缩放，从而达到数据预处理的目的。

2.2 融合标签信息的双图流形结构

为了充分地利用流形结构对分解过程的正则化约束，本文分别构建了两个图流形结构，在NMF分解过程中对分解因子V和U进行正则化处理。具体而言，首先构造一个真实的最近邻数据图G，并连接X= [x1,x2,...,xn]中的近邻点。为方便起见，采用0-1加权法构造数据图的权重矩阵，定义为

为提高数据图结构的正则化能力，将部分原始标签信息引入图结构中，有V=AZ，其中Z为辅助矩阵，A为标签约束矩阵，并带有原始标签约束信息。可将R(V)重写为

该流形图拉普拉斯矩阵为LU=DU −WU。

2.3 L2,1/2范数稀疏约束

基于稀疏约束的方法可以发掘特征空间的潜在关联，很多研究表明稀疏约束可以选择鉴别性稀疏特征来提高算法的效率和有效性，稀疏约束旨在使用适当的稀疏模型来实现稀疏数据表示。该方法通常使用Lp,q的范数形式对分解过程进行约束，是一种常见的提高矩阵分解性能的方法。例如，SNMF[12]在分解过程中对分解因子施加L2范数稀疏约束使因子更加稀疏，SGCNMF[5]在全局分解误差上添加L2,1范数稀疏约束使分解误差更加平滑，RGNMF[19]在输入数据的噪声中添加L1范数约束，以提高对噪声特征的屏蔽能力，但是近年来Xu等人[20]发现Lp为标准范数，且q为1 /2 时，即Lp,1/2类的范数约束具有较好的稀疏性约束。因此，S3GNMF算法的基矩阵U上的L2,1/2范数稀疏约束为

将| |U||2,1/2作为正则化项加入目标函数，在优化目标函数时，使用最小化L2,1/2范数能保证矩阵行列均稀疏，可以提高矩阵整体的稀疏性，使算法局部特征特异性降低，既可以降低噪声对算法的影响，又可以提高算法的泛化能力与计算速度。

2.4 S3GNMF目标函数

通过将特征缩放、R(V),R(U)、稀疏性约束和NMF集成到目标函数中，从而可以得到S3GNMF算法的目标函数为

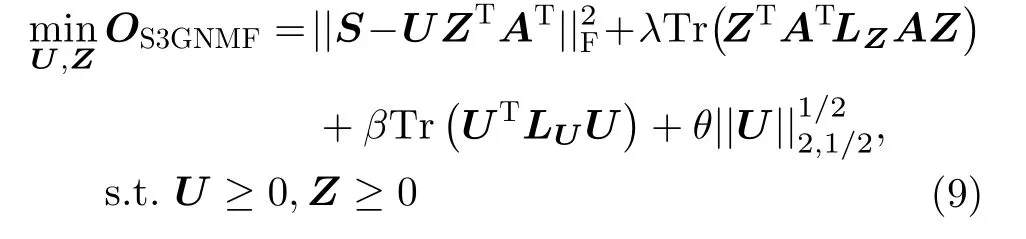
其中，λ,β为流形图正则化系数，θ为稀疏系数，S为输入原始矩阵的Sinkhorn距离特征缩放结果。

3 S3GNMF算法求解

由于S3GNMF算法的非凸性，很难获得全局最优解，所以我们采用梯度下降法来优化目标函数。将算法的目标函数展开重写为

4 实验结果与分析

标准的图像数据集中图像数据大多是对齐且居中的，而在现实世界中，真实图像可能十分复杂而且主体难以居中，导致无法完美地对齐；在校准主体后仍可能存在局部变形。这些问题均会导致针对标准数据集设计的算法性能受到极大的影响。所以我们尝试在多类标准数据集与非对齐的平移噪声数据上进行算法子空间聚类实验。在第1个实验中，本文使用多种算法对5个标准数据集分别进行了聚类实验，并表明了本文所提算法对标准对齐数据有着更强的子空间学习能力，在第2个实验中，本文使用小范围随机平移的COIL20数据集来模拟非对齐数据，并证明了本方法比以往方法具有更强的鲁棒性。为了公平地比较验证各算法在多方面的有效性，本文将所提算法与其他各NMF算法结果进行比较，所有的实验均基于MATLABR2018b模拟，CPU为Intel Core I7-9700 K。

表1 基于Sinkhorn距离特征缩放的多约束非负矩阵分解算法S3GNMF (算法1)

4.1 数据集

本文基于COIL20与Faces95数据集设计了2个平移噪声数据集，分别在2个平移噪声数据集与5个标准数据集(COIL20, PIE, Faces95, Pixraw10P,JAFFE)上进行了聚类实验，数据集详细说明如表2所示。

表2 各数据集的详细说明

需要注意的是，所有的标准数据集全是对齐数据，为了考验所提算法针对非对齐数据的学习能力，本文使用小的随机平移来模拟局部变形并在新的数据集上测试了本文方法，以显示其鲁棒性。具体来说，本文的数据集是由以下方法生成的：将数据集中每张图片调整为( 32−ω)×(32−ω)大小，其中ω∈[1,4]的整数，然后将调整的图像以随机位置放入32×32的空白图像中，图2–图6展示了上述数据集原始数据以及原始数据与平移噪声数据对比。

图2 PIE数据集

图3 Pixraw10P数据集

图4 JAFFE数据集

图5 COIL20数据集与平移噪声数据集对比

图6 Faces95数据集与平移噪声数据集对比

4.2 参数分析

如上所述，将Sinkhorn距离特征缩放过程中的两个参数α和ε设为固定值(α= 10,ε= 100)，所以本节主要讨论λ,β,θ3个约束参数。在参数对比实验中，本文在COIL20, PIE, Faces95, Pixraw10P和JAFFE 5个标准数据集，以最大类别数做聚类对比，可以得出最佳的参数组合。例如：COIL20数据集以20作为k值，然后分别使λ,β,θ以[0.001,0.01, 0.1, 0, 1, 10, 100, 1000]，进行20次综合实验，取最终聚类结果的平均值做对比，S3GNMF参数对比实验如图7所示。图7中每个点的位置代表了λ, β, θ3个参数的具体值，颜色代表了实际的聚类精度，颜色越黄，表示实际聚类精度越高，颜色越蓝表示聚类精度越低。

由图7得知，λ和β作为流形正则化参数，β的取值在10以上时能取得较好效果，λ更多的是作为特征空间的约束，做整体子空间表达的一个微调，参数取值不宜过大，当λ取值到1000时，对整体算法效果有负反馈。稀疏系数θ在上述实验过程中，更多起到的是对分解因子的稀疏约束与平滑噪声中野值点作用，对准确度提升不大，但是对算法性能稳定性有显著提升。

图7 S3GNMF在5个标准数据集上的参数表现

4.3 聚类结果与分析

本实验中，以本文所提算法S3GNMF与多个先进NMF算法(NMF[21], CNMF[13], GNMF[10], SNMF[12], SDNMF[11], DSDNMF[22], SODNMF[23],AGNMF[24], ONMF[25], DENMF[26])对上述5个数据集进行子空间学习聚类对比，聚类评价指标为准确度(ACcuracy, AC)与归一化互信息(Normalized Mutual Information, NMI)，对应指标越高则表明子空间特征学习能力越强。由于S3GNMF, CNMF,SODNMF, DENMF算法需要部分标签信息，上述半监督NMF方法均抽取了实验数据集的前20%的数据标签作为标记样本。所有的算法最大迭代次数为100，对比算法参数均为参考文献中的最佳参数(例 如S O D N M F 取α=100, β=0.01, θ=0.1)，S3GNMF的参数设置为4.2节中实验对比得出的最佳参数组合，实验流程如下：

(1) 以原始数据集作为输入数据，实验中设置k值为数据集的最大类别数，并作为k−means的聚类数；

(2) 以学习到的低维子空间特征表示作为输入，进行k −means聚类，对聚类结果进行AC和NMI评估；

(3) 重复执行步骤(1)和步骤(2) 20次，取其平均值与标准差作为最终实验结果。

表3显示了不同算法在5个数据集上的详细聚类结果(每个聚类实验中有两行数据展示，第1行数值代表聚类准确度，第2行数据代表归一化互信息)。

表3 各算法在标准数据集上的对比(%)

各算法在两个平移噪声数据集上的聚类实验结果如表4和表5所示，其中ω表示空间平移尺度，ω越大，平移越剧烈。

表4 各算法在平移噪声COIL20数据集上的对比(%)

表5 各算法在平移噪声Faces95数据集上的对比(%)

为验证本文所提Sinkhorn距离特征缩放的作用，在S3GNMF基础上移除特征缩放处理后，得到新的算法为(Semi-Supervised sparse and dual-Graph regularized Non-negative Matrix Factorization, S2GNMF)，S2GNMF与S3GNMF在上述多个数据集的详细聚类结果如表6所示。

表6 S2GNMF与S3GNMF的聚类效果对比(%)

上述实验数据表明：

(1) 基于流形正则化的算法GNMF, SDNMF,DSDNMF, SODNMF, AGNMF, DENMF, S3GNMF在实验中表现要明显优于其他非流行正则化算法，证明了子空间学习中流形正则化在隐式结构的重要性。

(2) 基于稀疏约束的各类算法在实验中，准确度和归一化互信息的标准差均低于其他非稀疏约束算法，证明了稀疏约束能增加局部学习能力与鲁棒性。

(3) 对于半监督学习算法CNMF, DENMF,SODNMF, S3GNMF，多混合约束算法明显优于单一约束算法，即部分标签信息能提高算法的学习能力，但是仍然需要有其他的子空间学习增强方法来针对有效数据进行学习。

(4) 随着平移噪声强度的增加，S3GNMF算法的性能明显优于其他算法，证明了本文所提的Sinkhorn距离特征缩放与多约束的有效性，其中Sinkhorn距离特征缩放简化了特征矩阵的距离度量，平滑了特征矩阵中野值点对分解结果的影响，而结合多流形隐式结构的正则化使整体算法泛化能力得到了提高，结合L2,1/2的稀疏约束，使实验数据十分稳定，而且基矩阵表达的局部特征更为稀疏，更有利于子空间的学习表达。

(5) 由表6中S3GNMF和S2GNMF的对比结果可知，Sinkhorn距离对不同维度之间的关系更加敏感，能更好地捕获类间关联，所以S3GNMF中基于Sinkhorn距离特征缩放处理能有效地提高各特征类别之间的关联，从而提高NMF算法的子空间学习能力。

4.4 算法复杂度与速度对比

本节首先分析了S3GNMF算法的复杂度，并讨论了几种对比算法的复杂度，最后设计了一组实验来计算各算法实际运算时间。

接下来本文对比了各算法在COIL20, PIE,Faces95, Pixraw10P和JAFFE 5个数据集上的运算速度，来验证算法的实际计算速度。实验中各算法单独运行20次，且设定最大迭代次数为100，k为数据集最大样本种类数，将最终耗时平均值作为对比数值，详细对比数据如表7所示。

由表7可知，SNMF算法分解效率最高，因为适当的稀疏约束有利于算法速度的提高；而以Sinkhorn距离作为损失函数度量方法的SDNMF与DSDNMF计算十分缓慢，这两种方法对平移噪声有一定的鲁棒性提升，结合流形图结构正则化也提高了算法性能，但是计算效率十分低下，其根本原因是Sinkhorn距离计算消耗极大，算法每次迭代均以分解因子的乘积与原始矩阵做距离对比，导致算法计算效率极低。基于欧氏距离的损失函数方法则明显速度更优，AGNMF算法虽然也有着不错的子空间学习能力，但是与SDNMF，DSDNMF算法类似，均在每次迭代中需要进行重复的耗时计算，导致整体运行速度不高，本文所提S3GNMF算法将Sinkhorn距离提取至迭代过程之外，直接对原始矩阵做缩放处理，避免了对Sinkhorn距离的反复计算，结合多流形正则与稀疏约束等，提高了算法性能的同时也提高了算法速度。

表7 各算法在不同数据集的运算速度对比(s)

5 结论

本文基于Sinkhorn距离特征缩放结合多流形学习和半监督稀疏非负矩阵分解，提出一种多约束非负矩阵分解算法S3GNMF。首先利用Sinkhorn距离对输入矩阵进行特征缩放，在充分利用缩放矩阵的流形图结构正则化与部分标签信息约束的同时，向基矩阵添加了高效的L2,1/2范数稀疏约束，并通过KKT条件推导出算法的乘法交叉更新规则。实验结果表明，S3GNMF算法不论是在标准数据集或是平移噪声数据集上，都取得了十分优秀的子空间学习结果，具有良好的鲁棒性，相比于SDNMF与DSDNMF算法，其在大幅度提高算法速度的同时，也提升了算法的性能。但本算法在运算速度上仍有优化空间，相较于其他单约束NMF算法，不仅运算复杂度更高且运算速度更慢，所以未来将着重研究具有高性能的NMF算法，并将所提算法结合应用在不同的领域[27,28]，如信息推荐、图像标记、网络安全等。