基于导向矢量双层估计和协方差矩阵重构的稳健波束形成算法

吕 岩 曹 菲 杨 剑 冯晓伟

①(火箭军工程大学核工程学院 西安 710025)

②(中国人民解放军 96746部队 库尔勒 841000)

③(火箭军工程大学导弹工程学院 西安 710025)

1 引言

目前，按一定最优准则形成方向图的波束导向阵列天线被称为智能天线，也被视为自适应阵列[1,2]。智能天线本质上意味着可通过计算机对天线进行控制，这将大幅提升阵列系统的性能[3]。自适应阵列处理技术能够根据信号环境实时调整阵列天线的权值矢量，利用自适应波束形成算法将波束图的主要增益指向期望信号(Signal Of Interest, SOI)方向，并抑制其他方向上的干扰信号[4,5]。该技术已被广泛应用于雷达、声呐、麦克风阵列语音处理、医学成像、无线通信、天文学和地震学等领域[6–8]。然而，自适应波束形成算法对信源误差和传感器误差非常敏感，例如信号方向误差、传感器位置扰动、幅度和相位误差等。特别是当SOI分量存在于数据快拍中时，波束形成器的性能将会严重下降[9]。因此，有必要提高自适应阵列处理中波束形成算法的稳健性。近几十年来，许多稳健自适应波束形成(Robust Adaptive Beamforming, RAB)算法相继提出，如对角加载(Diagonal Loading, DL)算法、特征子空间方法、不确定性集约束算法和协方差矩阵锥化(Covariance Matrix Taper, CMT)方法[10–12]，上述方法对于信号方向误差和传感器位置扰动是有效的，并且在某些失配条件下，能够提高阵列输出的信干噪比(Signal to Interference plus Noise Ratio, SINR)。然而，这些算法的采样协方差矩阵(Sample Covariance Matrix, SCM)无法剔除SOI分量，这一性质限制了算法在高信噪比(Signal to Noise Ratio, SNR)条件下的性能。

为了消除SOI分量的影响，已经提出了许多基于干扰加噪声协方差矩阵(Interference plus Noise Covariance Matrix, INCM)重建的RAB算法。文献[13]首先通过结合Capon功率谱(Capon Power Spectrum, CPS)估计和SOI角扇区分离区域的积分来重构INCM。随后，通过求解2次约束2次规划(Quadratically Constrained Quadratic Programming, QCQP)问题修正SOI的导向矢量(Steering Vector, SV)。为了提升CPS估计的分辨率，文献[14]推导了互质阵列的INCM重构算法，虽然分辨率得到了提高，但大幅增加了算法的复杂度。文献[15]基于两个子空间相交处的SVs重构INCM，这可使估计的SV更准确。文献[16]提出了基于SV和功率估计的INCM重构算法，但信源波达方向(Direction Of Arrival, DOA)的初步估计由CPS峰值搜索完成，这将使算法受限于CPS估计的分辨率。文献[17]描述了一种基于空间功率谱采样的低复杂度RAB方法，但该方法需要大量阵元才能达到与文献[13]相近的性能。文献[18]提出了一种基于梯度向量修正的SV估计方法，但本质上该算法仍受限于CPS估计的分辨率。文献[19]通过残余噪声消除和干扰功率估计提出了一种基于子空间的RAB算法，该算法需进行较多的矩阵乘积和求逆运算，增加了复杂程度。综合以上分析可知，多数INCM重构算法忽略了CPS估计的分辨率，当干扰信号角度接近时，CPS估计将无法有效区分信源的DOA，这将导致INCM重构误差。

尽管邻近干扰可通过零陷展宽[20]技术予以解决，但零陷展宽算法未必能够精准地在干扰方向上形成较深零陷，这可能影响阵列输出的SINR。并且，该类算法可能导致波束图的副瓣电平升高或主瓣展宽，在各种信号模型失配时的稳健性尚有待验证。针对以上问题，本文提出两种RAB算法。所提算法通过搜索CPS峰值确定积分区间，然后对各区间积分所得的协方差矩阵进行特征值分解。将较大特征值所对应的特征向量作为信源SV的初步估计，而后采用两种方法估计其与真实SV之间的误差，得到双层估计的SV和信源功率。最后通过重构INCM获得阵列最优权值矢量。计算机仿真实验验证了所提算法有效解决了CPS估计分辨率低的问题，较其他算法具备更好的综合性能。

2 信号模型

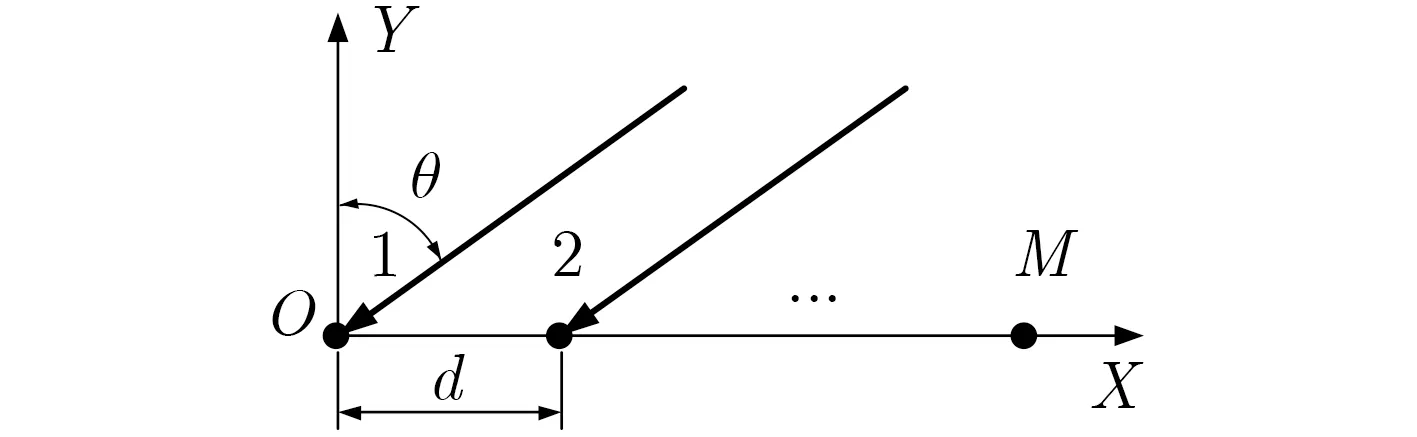
图1 线性阵列模型

3 关于CPS估计的分析

3.1 CPS估计的局限性

由于CPS估计只需已知阵列的结构信息，不需信源数等其他先验信息，所以目前多数基于INCM重构的RAB算法利用CPS估计入射信号的DOA或功率信息。但对于DOA估计，CPS估计技术的分辨率较低，因此当两个干扰信号角度接近时，其功率谱将会叠加重合，此时通过CPS仅可观察到一个峰值，这一局限性势必会导致RAB算法的输出SINR受到损失。下面将通过仿真验证CPS估计的局限性，假设1个功率为25 dB的SOI以−5◦到达10阵元的均匀线阵，3个干扰信号的干噪比(Interference to Noise Ratio, INR)同样为25 dB，分别以非邻近信号(入射角为−30◦,30◦和4 0◦)和邻近信号(入射角为−30◦,36◦和4 0◦)两种场景入射该阵列，快拍数K=30，图2为两种场景的CPS估计结果，所得曲线为200次蒙特卡罗实验的平均值。

图2中红色虚线代表非邻近场景，此时CPS估计可准确分辨出所有入射信号。蓝色实线表示邻近干扰场景，可以看出当两个信号入射角接近时，其CPS将会彼此重合叠加，估计的DOA也会发生偏移。

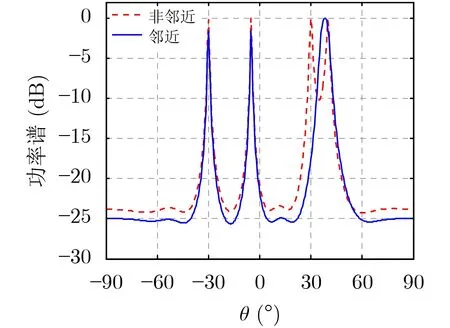
图2 两种场景的CPS

3.2 CPS和SV夹角的关系

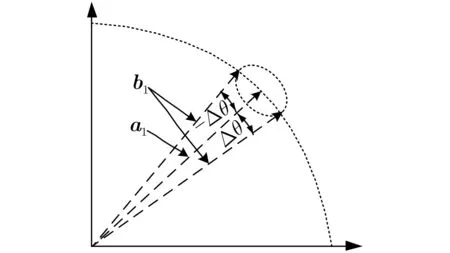
图3 估计SV和真实SV的关系示意

4 所提算法

4.1 重构INCM

为解决入射角接近时，CPS估计会出现叠加偏移的问题，所提算法首先利用式(17)计算入射信号所在区间的积分，获得与入射信号相关的全部信息

根据图4可知，积分区间内的信号数量和信号模型是否存在误差对特征值的幅度影响较大，但通过合理设置门限值(γ=0.95)，能够准确地区分积分区间内所含的信号数量，即可得参数η，并且所设门限对邻近或非邻近干扰条件均适用。此时，可将特征向量vη作为阵列入射信号SV的初步估计，选取η个较大特征值所对应的特征向量进行后续分析，接下来将提出两种方法修正vη，使其尽量与信源的真实SV接近一致。

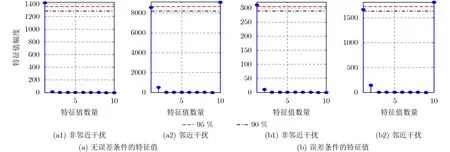
图4 特征值分布

方法1 显然，vη与Rˆl的最小特征值所对应的特征向量vM正交，即vηHvM=0 。通过向vη添加一个由其正交向量vM组成的比例梯度，并归一化模值，可得

其中，e⊥为修正SV和aˆl(θl) 之间的误差，ξ代表e⊥的上界。式(23)与不确定集约束算法的不同之处在于添加了aˆl(θl)和e⊥正交的约束条件，目的在于限制算法在aˆl(θl)的正交空间更加精准地搜索最优值。式(23)为2次优化(Quadratic Programming,QP)问题，可使用凸优化(ConVeX optimization,CVX)工具箱[21]求解。最终可得a˜l(θl)=aˆl(θl)+e⊥和P˜(a˜l)，并利用式(21)和式(22)得到重构的INCM。

4.2 SOI的SV估计

SOI的SV同样可使用所提算法进行估计，记为a˜s=a˜0(θ0)。综上，可得权值矢量

4.3 算法步骤及复杂度分析

5 仿真分析

仿真基于10阵元的均匀线阵，阵元间距为入射信号半波长。SOI的DOA为–5°，3个干扰信号的DOA分别设置为–30°, 36°和40°，INR=25 dB，积分区间限定为CPS峰值所在位置±8°范围内，积分角度间隔设置为 ∆θ=0.5°。当比较RAB算法的输出S I N R 和输入S N R 关系时，快拍数设置为K=30，当对比输出SINR随快拍数的变化关系时，SNR设置为20 dB，仿真实验所得的结果均为200次蒙特卡罗实验的平均值。

为进一步验证算法的性能，将所提算法与基于子空间的RAB算法[12]、基于CPS积分的算法[13]、基于CPS峰值搜索和功率估计的算法[16,18,19]性能进行对比。对于文献[12]算法，假设信源数为已知；文献[16]算法的参数设置为L=7；对于文献[18]，设置∆θl=10◦,η˜ =0.1 和N=20；文献[19]算法设置N=3 ；对于所提算法1，设置D=0.1,C=20和γ=0.95 ；所提算法2中设置参数ξ=0.01。

表1 所提算法步骤

实验1 波束图对比。在第1个实验中，主要检验RAB算法在信号模型无误差的条件下，生成波束图的性能。快拍数设置为K=30, SNR=20 dB，利用式(9)和式(12)计算各个算法生成的波束增益如图5所示。

根据图5可知，所有算法均能将波束主瓣指向SOI，并在−30◦方向形成零陷，然而文献[12,16,18,19]算法无法精确地在两个邻近干扰方向同时形成零陷，进一步验证了CPS估计的分辨率局限性，这必将对阵列输出的SINR产生影响。由于文献[13]算法对除SOI所在的区域进行整体积分，重构的INCM中包含干扰信号的全部信息，所以可在 36◦和4 0◦方向同时形成零陷。所提算法首先通过区间积分矩阵的特征值分布判定所含信号数量，又按照INCM的理论形式进行重构，所以形成的零陷比文献[13]更深。此外，由于所提算法2采用改进不确定集约束的思想对SV进行精准估计，因此形成的零陷优于算法1。

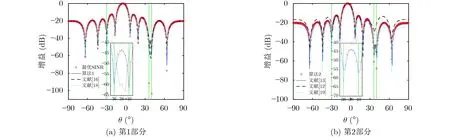
图5 波束图

实验2 DOA随机误差。在本实验中，主要检验SOI和干扰信号DOA均出现随机误差条件下对阵列输出SINR的影响，其真实DOA随机分布在区间[θl −5◦,θl+5◦]内。图6(a)为阵列输出SINR随输入SNR的变化趋势，可知文献[12]算法随着SNR的增大性能迅速下降，由于重构的INCM中包含全部的干扰信号信息，所以所提算法和文献[13]算法性能要优于其他算法。图6(b)为所提算法和文献[13]算法与最优SINR之间的偏差，由图可以看出算法2与最优SINR之间的偏差最小，并且输出曲线较为稳定，未出现大幅波动。图6(c)为输出SINR随快拍数的变化情况，根据图6(c)可知在快拍数小于20时，所提算法输出的SINR和文献[13]相近，当快拍数大于20后，所提算法输出的SINR高于其他算法且曲线平缓，输出较为稳定。

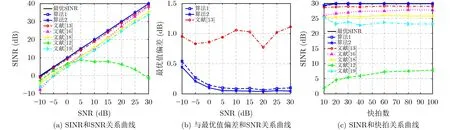
图6 DOA随机误差的测试结果

实验3 幅度误差和相位扰动。在第3个实验中，主要考察RAB算法对于接收信号的幅度和相位扰动误差的稳健性。当信号模型存在幅相误差时，式(2)的第m项可表示为

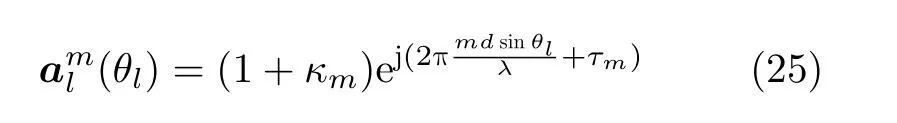
其中，κm为高斯分布N(1,0.052)，表示幅度误差，τm代表相位误差，服从N(0,(5◦)2)的高斯分布。图7分别为阵列输出SINR随输入SNR的变化趋势、与最优SINR之间的偏差和输出SINR随快拍数的变化情况。根据图7可知，所提算法和文献[13]算法的输出SINR高于其余算法，随快拍数变化较为稳定，但SNR较低时文献[13]算法性能优于所提算法，随着SNR逐渐升高，所提算法2性能达到最优。

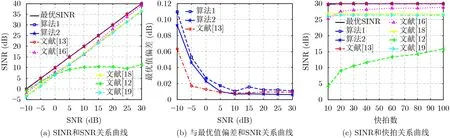
图7 幅相误差的测试结果

实验4 非相干局部散射。在本实验中，主要测试SOI的非相干局部散射对波束形成器性能的影响。假设SOI具备时变性质，则可表示为

其中，Φ{·}表示取矩阵最大特征值所对应的特征向量。非相干局部散射条件下的测试结果如图8所示。分析图8可知，所提算法和文献[13]算法的性能超过了其他算法，所提算法2的性能优于算法1，且输出较为稳定，文献[13]算法随SNR增大，输出的SINR出现了一定程度的波动。

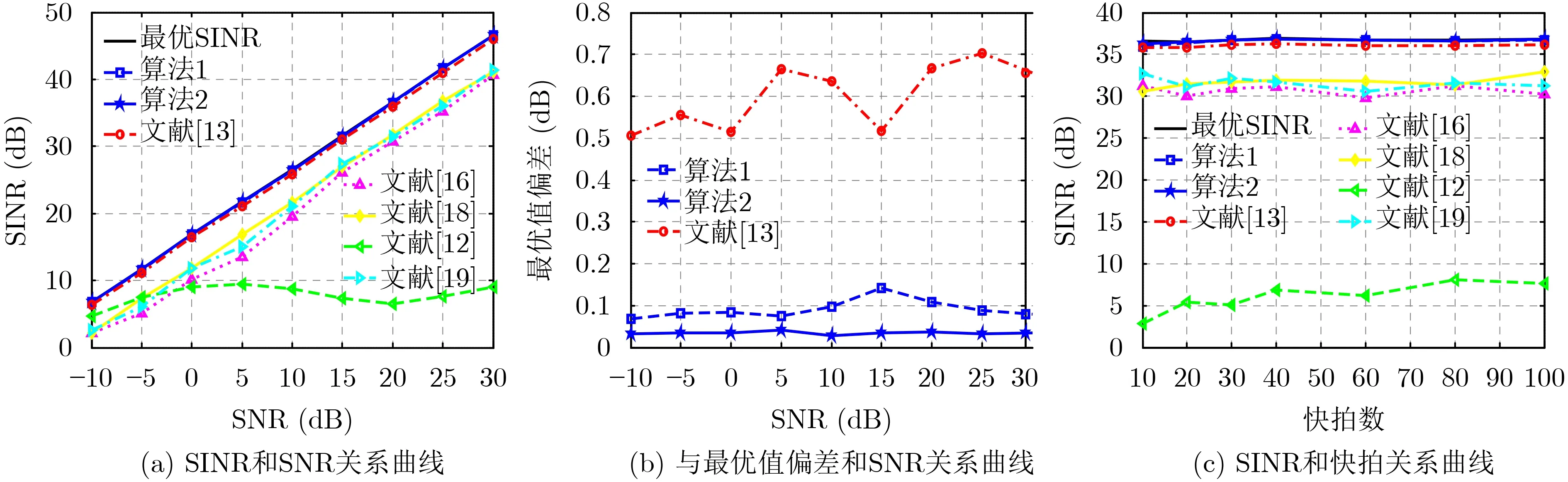
图8 非相干局部散射的测试结果

实验5 阵元位置扰动加DOA随机误差。在最后一个仿真实验中，主要测试RAB算法在信号模型同时存在阵元位置扰动和DOA随机误差复杂条件下的性能。此时，假设阵元位置在[−0.05λ,0.05λ]的范围内随机扰动，DOA误差的条件设置同实验2。图9(a)为阵列输出SINR随输入SNR的变化趋势，可知SNR较低时，文献[12]算法输出的SINR高于其他算法，随着SNR的逐渐增加，文献[12]算法性能下降，所提算法达到最优。图9(b)为与最优SINR之间的偏差情况，由于信号模型失配严重，条件比较复杂，3种算法均出现了不同程度的波动。相比于文献[13]，所提算法的波动程度较小，且算法2与最优SINR之间的偏差最小，在高SNR条件下最为接近最优值。图9(c)为输出SINR随快拍数的变化情况，根据图9(c)可知所有算法的输出SINR随快拍数的增加均出现了一定程度的波动，但相比于其他算法，本文所提两种算法始终处于最优位置。

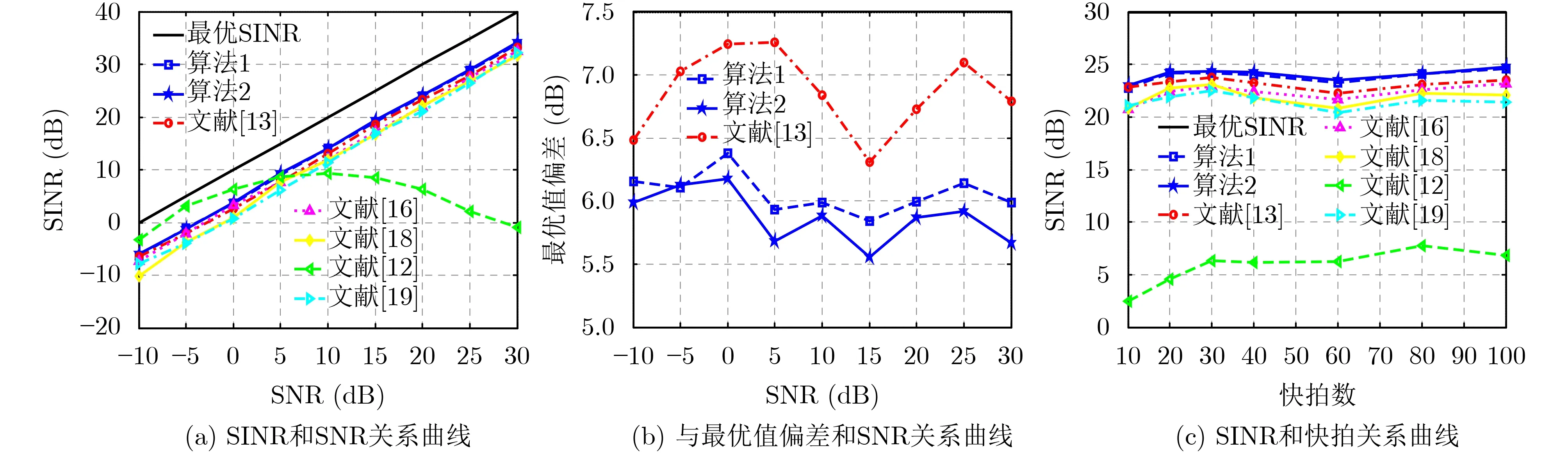
图9 阵元位置扰动加DOA随机误差的测试结果

6 结束语

针对INCM重构过程中CPS估计分辨率低的问题，本文提出两种RAB算法。所提算法首先通过搜索CPS的峰值确定积分区间，然后对各区间积分所得的协方差矩阵进行特征值分解，通过合理设置判定门限确定区间内所含的入射信源数量，并将较大特征值所对应的特征向量作为信源SV的初步估计。而后，所提算法1利用最小特征值所对应的特征向量，向初步估计的SV中添加正交比例梯度，得到双层估计的SV。与所提算法1不同，算法2通过求解QP问题得到修正的SV，最后通过重构INCM获得阵列最优权值矢量。通过无误差条件下的波束图、信源DOA随机误差、幅相误差、非相干局部散射和阵元位置扰动加DOA随机误差5个仿真实验的结果表明，算法2由于采用求解QP问题双层优化信源的SV，比算法1利用固定比例梯度的正交向量性能更优。此外，需要说明的是所提算法同样适用于非邻近干扰条件下的稳健波束形成。