多软件联合的拱坝三维数值建模方法及其应用

2022-12-28袁明道史永胜张旭辉彭汝轩

水力发电 2022年12期

谭彩，袁明道，史永胜，张旭辉，彭汝轩

(广东省水利水电科学研究院，广东广州 510610)

0 引言

准确地建立拱坝三维数值模型是保障其模拟结果可靠的重要前提，然而拱坝由于其体形复杂，精细化的三维拱坝数值模型建模耗时长、难度大，严重地制约了拱坝数值计算的发展[1-3]。因此，寻求一种简单、快速的三维数值建模方法是目前的重要研究课题之一。

多软件联合是目前最简单、最有效的三维数值建模方法之一，通过多软件协同作业发挥每个软件的优势，可极大地缩短建模时间，降低建模的难度[4-6]。朱权洁等[7]通过包括3DMINE、GOCAD、RHIRO和FLAC3D在内的7款软件进行联合建模，结果表明，联合建模方法建模速度快，且建模主要通过界面操作进行，降低了建模的难度，建模过程中数据逐步对接，减小了人为干扰误差。王飞[8]利用Excel-VBA、CATIA和有限元联合进行拱坝建模计算，通过多软件的联合使用，使建模过程模块化、参数化，缩短了建模的时间，提高了建模精度。李翔等[9]通过SURAPC、CAD、ARCGIS、ANSYS和FLAC3D对天祝煤矿进行三维建模并对该方法的可行性、有效性进行了验证。陈庆发等[10]对比了不同大型复杂地质体的三维建模方法，取长补短，提出了改进的3DMine-FLAC3D耦合建模方法，并将其应用于锌多金属矿取得了良好的成效。

综上所述，多软件联合在复杂三维地质体建模研究较为充分，但对具有复杂地质条件和拱结构的拱坝三维数值建模研究尚不够充分。因此，本文提出了一种多软件联合的拱坝三维数值建模方法，该方法联合AutoCAD、dxf2xyz、Surfer、SolidWorks、HyperMesh和有限元共6种软件进行建模，实现了拱坝三维数值模型简单、快速地构建。

1 建模方法

多软件联合的拱坝三维数值建模方法采用的软件有AutoCAD、dxf2xyz、Surfer、SolidWorks、Hyper-Mesh和有限元共6种，其建模方法流程如图1所示。首先采用AutoCAD建立带高程信息的地形等高线图，并保存成为dxf文件。通过dxf2xyz软件将dxf文件转化为坐标点文档，并将该文档可用记事本打开并另存为txt文件；其次采用Surfer软件中的Grid菜单下的Data工具导入*txt文件，并完成插值，插值完成后通过Grid菜单将曲面网格转化为顺序排列的*dat文件坐标点，设置逗号将顺序排列的dat文件坐标点X，Y，Z分隔，并采用SolidWorks将曲面处理光滑后拉伸成地质体模型，建立拱坝模型并完成地质体和拱坝模型的组装，并根据地质信息资料，进行切割分区，导出几何模型文件；再次将实体模型导入HyperMesh中进行网格划分，并对模型进行简单的附参，导出有限元模型文件；最后将有限元模型文件导入至有限元软件，完成建模。

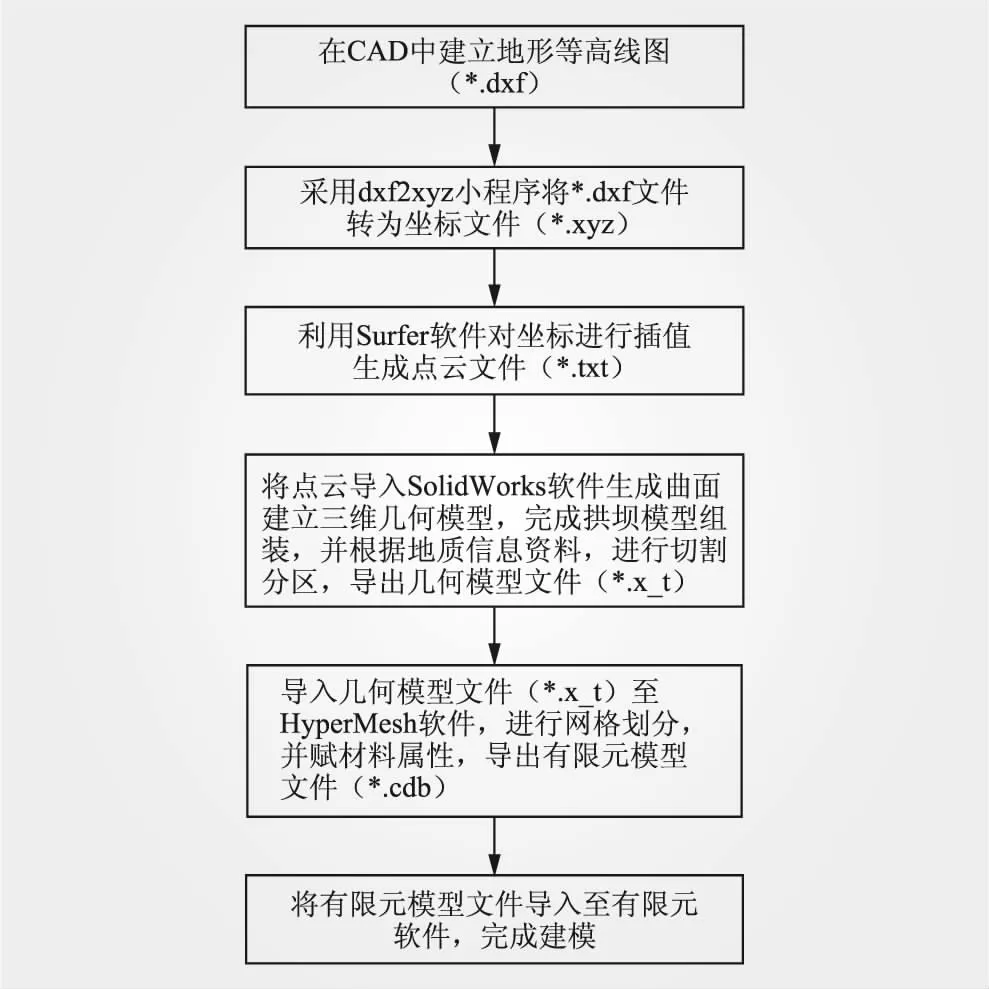
图1 多软件联合的拱坝三维数值建模方法流程

2 工程概况

天堂山水库位于东江支流，地处广东省龙门县境内，水库控制集雨面积461 km2，总库容2.43亿m3，是一座以防洪为主结合发电、灌溉和改善航运的综合利用的大型水利枢纽工程。工程于1989年9月截流，1990年元旦浇筑大坝混凝土，1993年9月全部投产。

天堂山水库大坝为混凝土双曲拱坝，坝顶高程159.00 m，最大坝高70.0 m，坝顶厚5.75 m，底厚22.04 m，顶弧长287.37 m，根据施工浇筑能力及溢洪道闸墩等布置要求，坝体分缝间距15～18 m，共20个坝块。河流在坝址处的流向为北西西到南东东，基本与坝址岩体的主要断层方向一致，河谷断面呈“V”字形，底宽35～40 m，坝顶159.00 m高程时宽约210 m，宽高比3∶10(开挖后宽高比约4∶1)，两岸地形较雄伟均匀，坡比35°～45°。

3 计算原理、模型与参数

3.1 计算原理

混凝土和岩土体均为弹塑性材料，按弹塑性增量理论进行计算。塑性应力-应变关系为

{dσ}=[Dep]{dε}

(1)

式中，{dσ}为应力增量；{dε}为应变增量；[Dep]为弹塑性系数，可表示为

(2)

对物理非线性问题，一般采用分段线性化的纯增量法和逐次迭代方法求解。

3.2 计算模型

有限元计算模型如图2所示。计算采用直角坐标系，x轴从左岸指向右岸，y轴指向下游，z轴竖直向上。模型底部采用固定约束，四周边界采用连杆约束。拱坝坝基的岩体采用空间六面体Solid45单元，即八结点等参单元。坝体采用Solid65单元，即八结点混凝土单元。整个计算模型的单元总数为21 785个，节点总数为27 484个。

图2 计算模型

3.3 计算参数

混凝土计算参数取值：容重γ为24 kN/m3；弹性模量E一般情况下取3.1×104MPa；低水位高温时取1.5×104MPa；泊松比μ为0.2；线膨胀系数α为0.000 01 ℃。坝基部分抗剪断强度采用值如表1所示。根据1990年～2013年天堂山拱坝现场温度监测资料以及原设计温度取值，确定本次计算温度取值如表2所示。计算假设作用于坝肩滑块侧滑面和底滑面上的渗压通过帷幕进行第一次折减(折减系数为α1)，经过排水幕进行第二次折减(折减系数为α2)，全程线性分布直至滑块下游出露处渗压变为0。帷幕折减系数α1=0.4，排水折减系数α1=0.2。作用于坝面单位宽度上的水平泥沙压力可按下列公式计算

(3)

γsb=γsd-(1-n)γw

(4)

式中，Psk为泥沙压力；γsb为泥沙的浮容重；γsd为泥沙的干容重；γw为水的容重；n为泥沙的孔隙率；hs为坝前泥沙的淤积厚度；φs为泥沙的内摩擦角。

表1 抗剪断强度参数

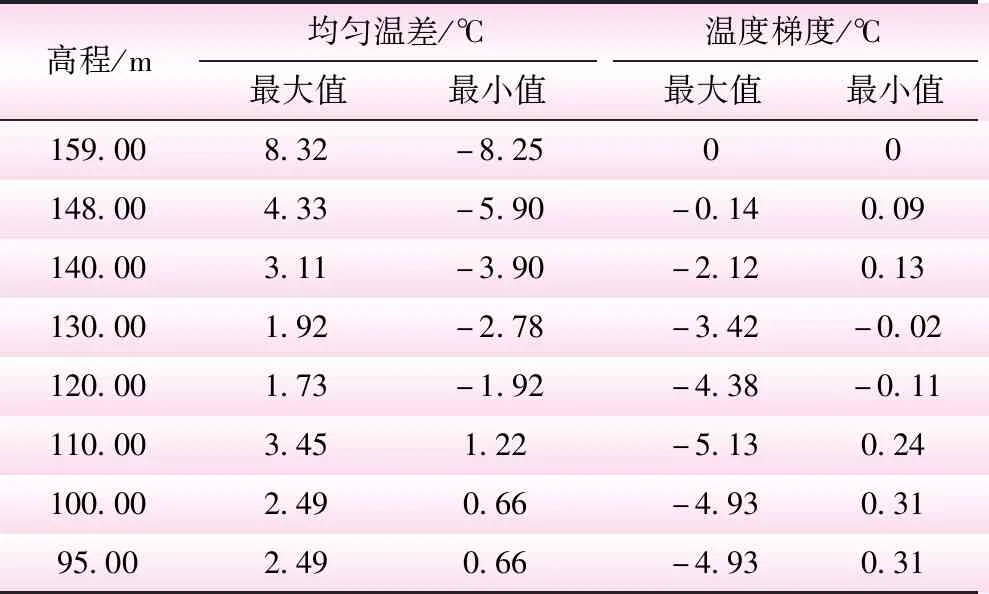
表2 计算温度取值

本次计算取泥沙淤沙高程120 m，淤沙浮容重γsb=5 kN/m3，淤沙内摩擦角φs=0°。

4 计算结果与分析

分别对正常蓄水位150.00 m、百年设计洪水位156.61 m和千年校核洪水位157.24 m共3种工况进行计算并与内力平衡分载法计算结果进行对比。不同工况下拱坝等效位移、等效应力云图分别如图3和图4所示，不同工况下有限单元法与内力平衡分载法计算的坝体最大应力和位移分析对比如表3所示。从图3、图4、表3可知，不同工况下，天堂山拱坝应力和位移虽数值不同但其变化规律基本一致，坝体下游面基本为压应力，而坝体上游面在坝踵位置附近出现拉应力，同一高程位移量值从拱冠至左右拱端逐渐减小。由于河谷形状基本对称，坝体左右半拱顺河向位移基本呈现对称性。坝体最大顺河向位移出现在下游坝面159.00 m高程拱冠处。正常蓄水位工况下，最大压应力值4.30 MPa，最大拉应力值1.09 MPa，最大位移12.9 mm；设计洪水位工况下，最大压应力值5.78 MPa，最大拉应力值1.17 MPa，最大位移19.8 mm；校核洪水位工况下，最大压应力值为6.05 MPa，最大拉应力值为1.28 MPa，最大位移21.4 mm。

图3 不同工况下拱坝等效位移云图(单位：m)

表3 坝体最大应力和位移分析对比

图4 不同工况下拱坝等效应力云图(单位：Pa)

通过对比分析有限单元法和内力平衡分载法计算结果可以看出，2种方法位移和应力分布规律基本一致，说明采用多软件联合的拱坝三维数值建模方法建立的有限元模型计算结果是可靠的。有限单元法计算拱坝所得的应力比内力平衡分载法计算结果大，这是由于有限单元法考虑了坝与地基的联合作用，地基中包括了风化层、蚀变带、复杂的地质构造及传力墙分布情况，而内力平衡分载法无法考虑。