钦州市农业科技进步贡献率的测算研究

占金刚 蒋学海* 詹满琳

〔1.北部湾大学经济管理学院，广西 钦州 535011；2.北部湾海洋发展中心（北部湾大学），广西 钦州 535011；3.北部湾大学机械与船舶海洋工程学院，广西 钦州 535011〕

农业的发展关乎国计民生，是国民经济发展的基础。从长期看，农业经济发展必将面临资源和环境的双重制约，以往单纯依靠要素投入来扩大农业经济增长的模式存在局限性。经济理论表明，农业经济增长不仅来源于要素投入的增加，还包括科技进步所带来的投入产出比的增加，前者强调的是增加要素投入，后者强调的是提高生产效率，因此学者普遍认为农业科技进步是农业经济增长最佳来源途径，而非要素投入。我国拥有全世界20%的人口，也是农业生产大国，我国农业经济基础薄弱，农业科技发展起步晚，这导致我国农业科技含量不高，发展方式依然以要素推动型的粗放模式为主。因此，提高我国农业科技进步是实现传统农业向现代农业转变的关键因素。

农业科技进步有广义和狭义之分，狭义的农业科技进步一般是指农业技术的进步，如生产机械升级、粮食种子改良等自然科学硬技术所带来的科技进步；而广义的农业科技进步不仅是指农业技术的进步，还包括生产管理水平、决策和服务水平等社会科学软技术所带来的科技进步。本文用Solow余值法测算的农业科技进步是指广义的农业科技进步，即农业经济增长中扣除要素投入贡献的部分就是农业科技进步所带来的经济增长，称之为农业科技进步贡献率。

美国数学家Charles W. Cobb和经济学家Paul H. Douglas（1928）［1］结合美国1899—1922年相关统计数据研究了生产要素对经济增长的贡献作用，发现只有资本和劳动才是经济增长的关键要素，而其他要素对经济增长的贡献小到可忽略不计，这一发现衍生出Cobb-Douglas生产函数。Cobb-Douglas生产函数在引入耕地要素之后，就可以用于描述农业经济增长的成因。之后，美国经济学家Robert M. Solow（1957）［2］结合Cobb-Douglas生产函数，首次分解出技术进步在经济增长中的贡献份额，并提出增长速度方程法即Solow余值法可以精确测量技术进步对经济增长的贡献率。除Solow余值法外，CES生产函数法、超越对数法［3，4］、DEA数据包络分析法［5］、丹尼尔森因素分析法等也常被用于测量农业科技进步贡献率。

自20世纪80年代我国引入农业科技进步贡献率之后，国内相关研究众多，其中Solow余值法因其科学、便捷等特点，应用最为普遍。国家计委和国家统计局在1992年、农业部科技司在1997年曾分别下发通知，推荐采用Solow余值法作为测算农业科技进步贡献率的基本方法。这之后，Solow余值法更是被国内学者广泛运用。全国层面，朱希刚等［6］指出Solow余值法适合测算我国农业科技进步贡献率，并对“八五”期间全国及各省农业科技进步贡献率进行了实际测算，结果显示“八五”期间我国农业科技进步贡献率仅为34.3%。胡凯［7］利用Solow余值法测算了我国1978—2010年间各要素对农业总产出的贡献作用，研究发现我国1978—2010年农业科技进步贡献率为51.9%，并指出资本投入和科技进步是影响我国农业总产出的两个关键因素。更进一步，段婷婷［8］利用Solow余值法测算出我国农业科技进步贡献率由1995—2000年的24.7974%上升到2011—2013年的55.2833%。区域比较层面，牛凯等［9］基于C-D生产函数建立了固定效应变参数面板模型，对我国粮食主产区的农业科技进步贡献率进行测算。结果表明，我国粮食主产区农业科技进步贡献率区域差异比较明显，并指出我国农业科技进步对农业总产出的贡献作用仍然较小。马松林［10］基于Solow余值法比较了我国农业科技进步贡献率的区域差异，指出空间滞后模型（SEM）更适用于区域差异研究，结果表明，北京、上海、广东、浙江等经济发达地区的农业科技进步贡献率较高，而作为粮食主产区的河南农业科技进步贡献率较低，并提出了一些建议。省级层面的研究文献更加丰富，如对江西省［11］、海南省［12］、云南省［13］、内蒙古［14］的相关研究，这里不再描述。

综上所述，国内对农业科技进步贡献率的研究较多集中于国家和省级层面，对各市的研究相对较少，不少城市尚属空白。本文立足广西钦州市，基于Solow余值法对钦州市1996—2019年的农业科技进步贡献率进行测算分析，同时比较各要素对农业总产出的贡献作用，针对性提出钦州市未来农业发展的对策。

1 农业科技进步贡献率的测算方法

1928年，美国数学家Charles W.Cobb和经济学家Paul H Douglas在研究美国1899—1922年生产要素对经济增长的关系时，提出了著名的Cobb-Douglas生产函数Y=AKαLβ。此后，C-D生产函数被广泛应用于经济增长驱动要素研究中。由于耕地要素在农业生产中占有重要地位，因此在研究农业经济增长时需将其考虑进来。1957年，美国经济学家Robert M. Solow在C-D生产函数的基础上提出了综合要素生产论概念，并首创了增长速度方程法，即Solow余值法。这时，农业生产函数模型为：

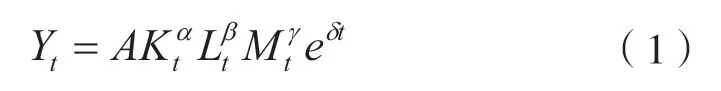
式中，Yt、Kt、Lt和Mt分别表示钦州市第t年农业总产出、资本投入、劳动力投入和耕地面积投入。α、β和γ分别表示资本投入产出弹性系数、劳动力投入产出弹性系数和耕地面积投入产出弹性系数，经济含义是指一单位Kt、Lt、Mt的增加将分别引起α单位、β单位、γ单位的Yt增加。A为常数，δ为农业科技进步率，是指因农业科技进步所产生的总产值增长率。

（1）式两边取对数，得下式：

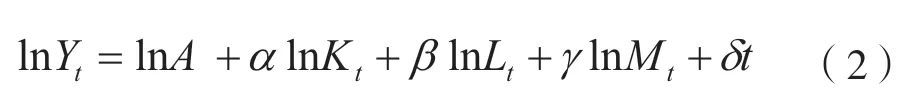
（2）式两边同时对t求导，可得

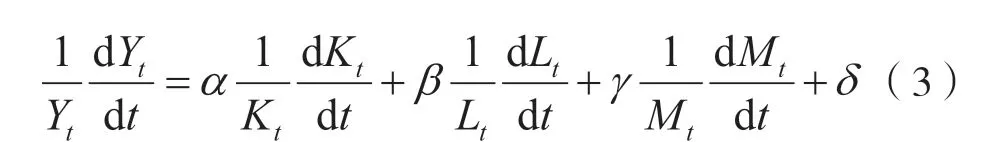
由于Yt、Kt、Lt和Mt都是年度数据，因此可令dt=1，这时ΔYt=dYt、ΔKt=dKt、ΔLt=dLt、 ΔMt=dMt，（3）式化简可得

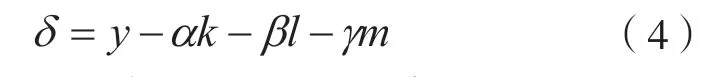
其中，农业总产出年均增长率y= ΔYt / Yt、资本投入年均增长率k= ΔKt / Kt、劳动力投入年均增长率l= ΔLt / Lt、耕地面积投入年均增长率m= ΔMt / Mt。

农业科技进步贡献率是指农业科技进步对农业总产出增长量的贡献份额，即科技进步率与总产值增长率之比，

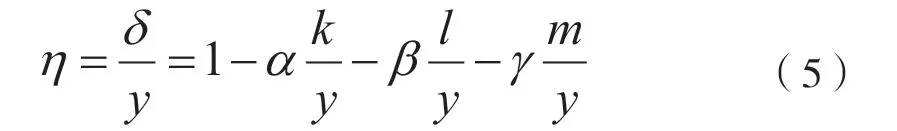
由此可见，要计算钦州市1996—2019年的农业科技进步贡献率，首先要获取这期间钦州市农业总产出、资本投入、劳动力投入和耕地面积投入各个数据，这在官方统计年鉴上可获得。其次要采用合理的年均增长率计算方法，从而得到y、k、l和m的值。除此之外，我们还需知道投入产出弹性系数α、β和γ的值，目前计算这些值的方法主要有经验参数法和回归法。经验参数法是指农业部综合全国情况，建议采用固定弹性系数α= 0.55、β= 0.20和γ= 0.25以计算我国农业科技进步贡献率，并根据各省差异，给出了投入产出弹性系数的调整公式。相对来说，经验参数法主观性较强，且钦州市相比全国、各省的统计范围较小，数据误差会很大，因此本研究不适合采用经验参数法。

回归法是指根据钦州市历年统计数据进行回归，可以直接得到钦州市1996—2019年各要素投入产出系数的值，客观性较强，因此适用于本研究。此外，假设钦州市1996—2019年农业生产规模报酬不变，农业科技进步模式是希克斯中性型，即有α+β+γ= 1。因此，为避免多重共线性，不妨在（2）式中代入γ= 1 -α-β，从而消去lnMt项，得到 下式：

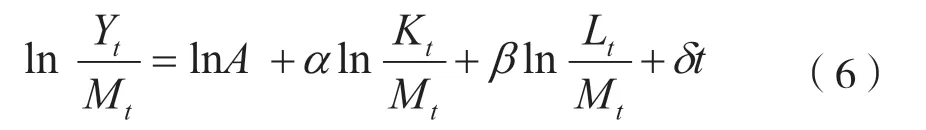
于是，根据相关统计数据，结合（6）式做回归分析，即可得到钦州市1996—2019年期间的α、β和δ值，再根据α+β+γ= 1可得γ的值。需要指出的是，在测算钦州市1996—2019年的科技进步率时不采用回归得到的δ值，而是通过（4）式计算得到，这是为了保证要素贡献率和科技进步贡献率之和为1。此外，在分析短周期时，本文仍旧采用1996—2019年的α、β和γ值，并通过（4）式计算得到这期间的δ值，这是因为回归法需要多个样本数据以增加可信度，在短周期采用回归法测算α、β、γ将存在较大误差。

2 钦州市农业科技进步贡献率的测算

2.1 指标选择与数据处理

指标的选择既要考虑到科学性，要能真实反映农业的投入产出情况，又要考虑数据的可获得性，因此作以下考虑。

农业总产出：在农业生产中，“农林牧渔业总产值”能够反映一定时期农业的产出情况，作为农业总产出的具体指标。为抵消物价变动的影响，本文选择1995年为基期，将钦州市1996—2019年农业总产值折算为1995年同期价格，折算系数选择广西农村商品零售价格指数，即“基期价农业总产值= 当年价农业总产值/当年农村商品零售价格指数×基期农村商品零售价格指数”。

资本投入：农业生产的物质费用投入可用“农林牧渔业中间消耗”指标表示，由于统计年鉴上无法直接获取该数据，结合相关定义，本文使用“农业总产值-农业GDP”表示农林牧渔业中间消耗。再者，为抵消物价变动的影响，本文采用上述做法，故而有“基期价农林牧渔业中间消耗=（当年价农业总产值-当年价农业GDP）/当年农村商品零售价格指数×基期农村商品零售价格指数”。

劳动力投入：本文选择钦州市“第一产业就业人数”，以年末人数来表示当年的劳动力投入。

耕地面积投入：考虑到部分年份的耕地面积数据缺失，且近年来耕地撂荒严重，故本文使用“农作物播种面积”来替代耕地面积投入。

以上所选择的数据主要来源于1996—2019年的《广西统计年鉴》，因统计指标改变，导致部分年限的相关数据缺失，这部分数据参考《钦州统计年鉴》和《中国区域经济统计年鉴》可得。1995—2019年钦州市投入产出数据见表1，价格已折算为基期价。

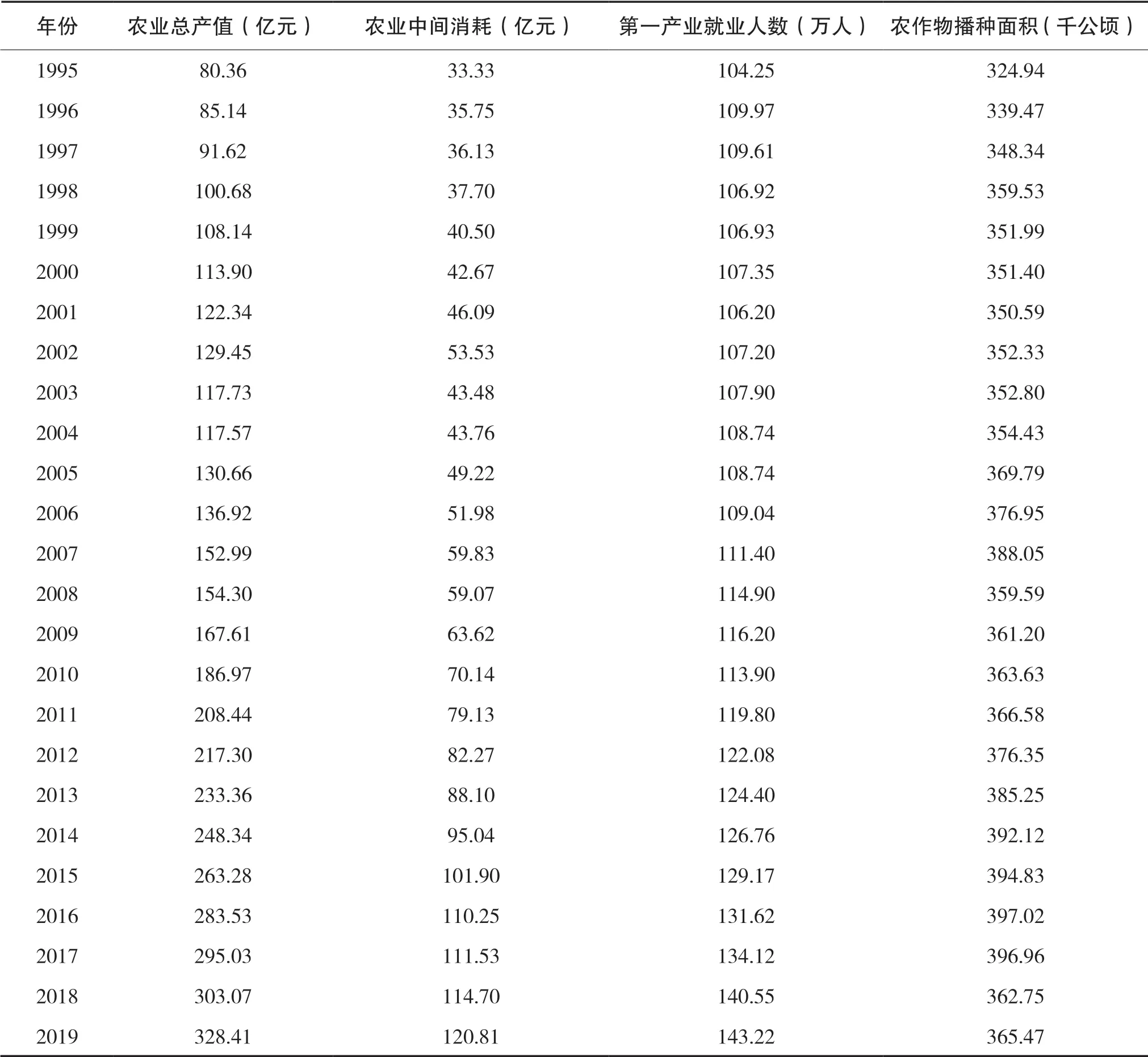
表1 1995—2019年钦州市投入产出数据（基期价）

时间变量：本文以1995年作为基期，1996—2019 年为研究期，因此1995年⇔t= 0、1996年⇔t= 1、…、2019年⇔t= 24。

2.2 各要素投入产出弹性系数的确定（WLS回归）

为了消除异方差的影响，本文选择做加权最小二乘回归（WLS）。1995—2019年钦州市投入产出数据（基期价）见表1，将表1相关数据代入（6）式，结合Eviews 10软件做WLS回归，方程（6）式的回归结果如图1所示。

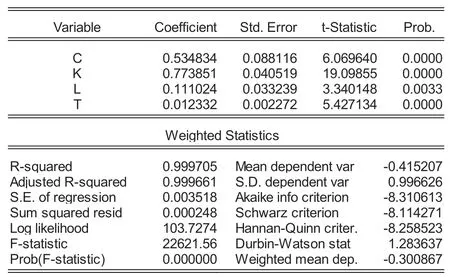
图1 方程（6）式的回归结果

回归方程R2=0.999705，修正的R2=0.999661，回归方程F=22621.56，通过1%的显著性检验（0.0000），说明回归模型的拟合程度较高，且回归模型总体显著，整体解释能力较强。此外，各参数均通过1%的显著性检验，说明各投入要素对农业总产值的影响也都是显著的，证明本文的回归结果较为良好。

因此，方程（6）式的回归结果为

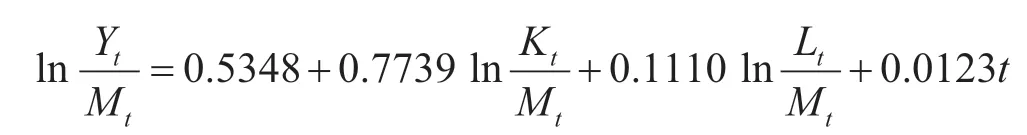
上式又可写成

由此可知钦州市1996—2019年的各要素投入产出弹性系数和科技进步率分别为α= 0.7739、β= 0.1110、γ= 0.1151和δ= 0.0123。

2.3 年均增长率的计算

一般来说，科技进步对经济增长的影响具有一定的持续性，短期内并不会被轻易替代，而且新技术的研发通常需要较长的时间，体现出科技进步对经济增长影响存在的周期性。科技进步对农业总产值的影响亦是如此，因此本文参考国家五年规划，将研究期划分为五个阶段，分别是1996—2000年（“九五”时期）、2001—2005年（“十五”时期）、2006—2010年（“十一五”时期）、2011—2015年（“十二五”时期）、2016—2019年（“十三五”前中期）。

按照已有文献的普遍做法，投入产出在某段时期的年均增长率可用这段时期的几何增长率表示，如农业总产值在t1—t2年间的年均增长率为

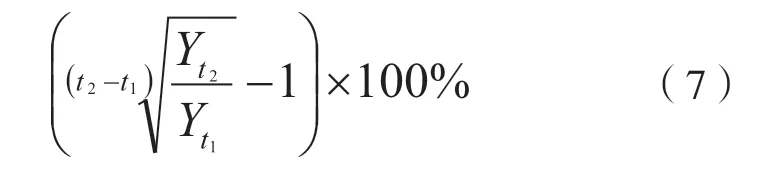
其中，Yt1、Yt2分别是钦州市t1、t2年的农业总产值。其他要素投入的年均增长率计算式同上，不再列出。

2.4 科技进步贡献率的计算

为了计算出钦州市各段时期的科技进步贡献率，首先需要得到各投入产出指标在各个时期的年均增长率。根据表1数据，结合（7）式，我们可以得到各指标的年均增长率。再者，根据钦州市1996—2019年各要素的投入产出弹性系数，结合（4）式又能得到钦州市在各个时期的科技进步率。具体如表2所示。

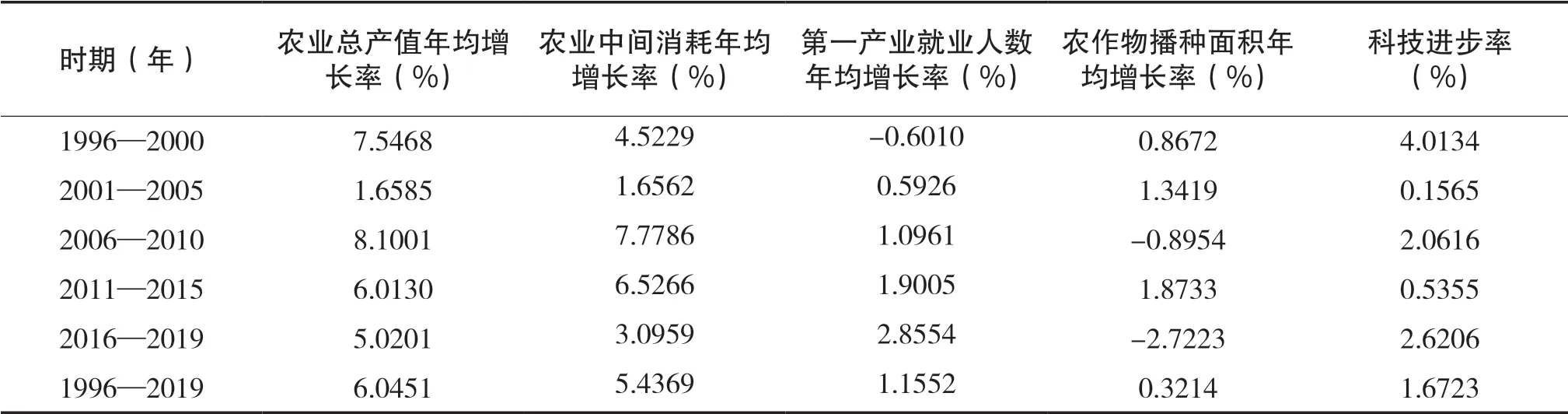
表2 各个时期钦州市投入产出指标的年均增长率及科技进步率

接下来，我们根据（5）式就可得到钦州市在各个时期的农业科技进步贡献率。其中，αk/y、βl/y、γm/y分别是指钦州市农业总产值的资本投入贡献率、劳动力投入贡献率、耕地面积投入贡献率。汇总得表3。

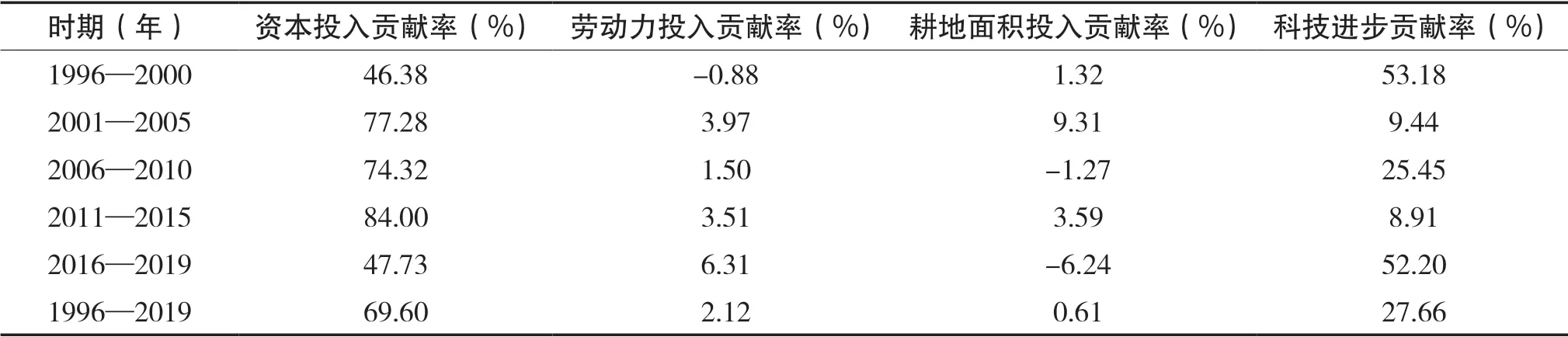
表3 各个时期钦州市农业生产的投入贡献率、科技进步贡献率

3 测算结果分析

3.1 投入产出弹性系数

根据前文回归结果，钦州市1996—2019年间资本、劳动力、耕地面积的投入产出弹性系数分别为α=0.7739、β= 0.1110、γ= 0.1151，经济含义是指每增加一单位资本、劳动力、耕地面积的投入，农业总产出将分别增加0.7739单位、0.1110单位、0.1151单位。不难发现，资本投入产出弹性系数最大，而劳动力和耕地面积投入产出弹性系数相当，说明钦州市在1996—2019年间资本投入对农业总产出的影响最为有效，而劳动力和耕地面积投入对农业总产出的影响作用相当，但都不及资本投入的影响，作用约只有其七分之一。

根据朱希刚的测算，我国农业生产领域里资本、劳动力、耕地面积的投入产出弹性系数分别是0.55、0.20、0.25，这一水平得到了农业部的认可并在全国范围推广采用，不少学者在研究时也大多采用这一标准，这就是经验参数法的应用前提。与全国平均水平相比，钦州市1996—2019年间的资本投入产出弹性系数较高，而劳动力和耕地面积投入产出弹性系数较低。根据经济学的边际贡献递减规律，如果某要素的投入产出弹性系数较高，则说明该要素的投入不足，应进一步增加投入，反之如果较低，则说明该要素的投入过多，应减少该投入。这就说明，钦州市1996—2019年间的资本投入不足，今后追加农业资本投入能够获得较大的边际贡献，而劳动力和耕地面积投入过多，边际贡献过低，应适当引导这些要素向其他产业进行转移，以提高生产要素的配置效率。

3.2 农业科技进步贡献率

各个时期钦州市农业生产的投入贡献率、科技进步贡献率见表3。由表3可知，钦州市1996—2019年间农业科技进步贡献率为27.66 %，而资本投入贡献率为69.60%，这表明钦州市整体上在1996—2019年期间属于要素推动型的粗放发展模式，农业科技进步的贡献作用并不突出。其他要素方面，劳动力、耕地面积投入贡献率微乎其微，分别只有2.12%、0.61%，远不及资本要素和农业科技进步对农业总产出的增长贡献。钦州市农业劳动力和耕地面积不论是对农业总产出的边际贡献，还是对农业总产出的实际贡献都普遍较低，一方面表明钦州市农业生产中出现比较严重的劳动力过剩现象，应及时引导农业劳动力向其他产业进行转移，以提高劳动力资源配置的效率，另一方面也表明钦州市农业生产效率较低，表现出单位耕地面积的农业产出值较低，耕地面积没有得到高效利用，农业生产管理方式较为落后。

钦州市各个时期的农业科技进步贡献率见图2。由图2可知，钦州市农业科技进步贡献率整体呈现“W”形变化。尽管钦州市1996—2019年间农业科技进步贡献率为27.66%，从表3中可知钦州市2016—2019年的农业科技进步贡献率为52.20%，远高于1996—2019年间的27.66%，同时与2020年我国平均水平60%较为接近，这说明钦州市近几年农业发展正从要素推动型的粗放发展阶段逐步走向科技推动型的集约发展阶段，农业科技进步在推动农业经济增长中逐步扮演重要角色。值得注意的是，钦州市在“九五”时期的科技进步贡献率就已超过50%，但在“十五”时期却骤降至10%，说明钦州市农业科技进步对农业总产出影响的稳定性差。整体而言，钦州市各时期的农业科技进步贡献率呈现30%±20%上下波动，推动农业科技进步贡献率的持续稳定增长成为当下亟须解决的一个问题。

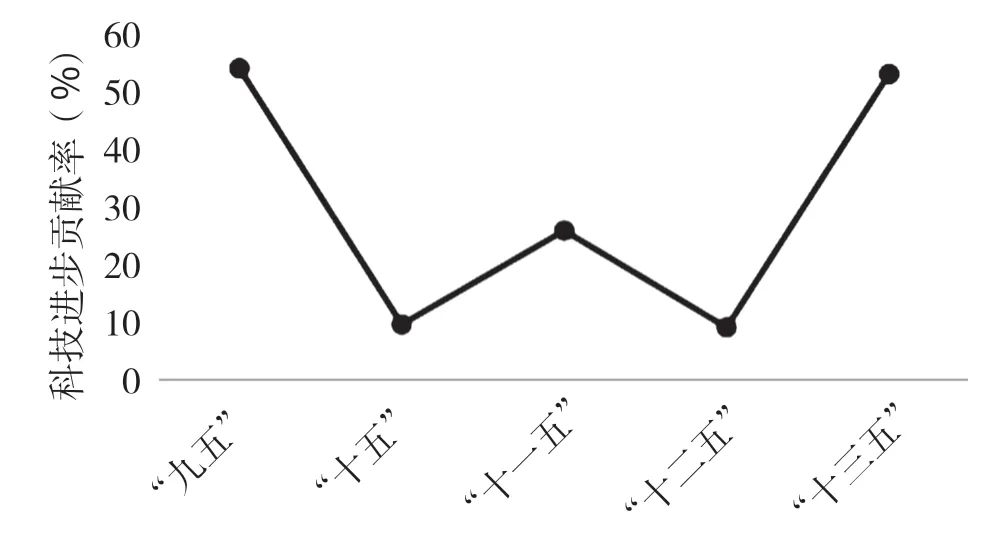
图2 钦州市各个时期的农业科技进步贡献率

4 对策建议

根据本文的测算结果，钦州市1996—2019年间的农业经济增长主要依靠农业资本要素的推动。但在近几年，钦州市农业资本投入的年均增长率和其对农业经济增长的贡献率逐渐下降，而农业科技进步贡献率逐渐增加，这表明钦州市已开始由要素推动型的传统农业逐步向科技推动型的现代农业转变。然而，根据对测算结果的相关分析，钦州市当下农业经济发展还存在一些问题。为推动钦州市农业经济和农业科技进步贡献率的持续稳定增长，本文提出以下建议。

4.1 组织农业劳动者生产管理技能的教育培训，提高耕地面积的生产使用效率，适量引导农业过剩劳动力向其他产业进行转移

劳动者生产管理技能的高低直接影响着生产要素能否合理配置、生产效率能否充分发挥，也是发展科技推动型现代农业、落实国家科技兴农战略的关键。当前，钦州市农业劳动者的生产管理技能普遍较低，导致耕地面积的生产效率较低、农业劳动力过剩等问题。对此，政府一方面应加强劳动者技能教育，积极深入基层开展生产管理技能培训和推广农业科学技术，切实提高耕地面积的生产效率；另一方面应适当引导农业过剩劳动力向其他新兴行业转移，切实提高全行业劳动力要素的配置效率。

4.2 现阶段应适当加大农业资本的投入力度，发挥其对农业总产出高边际贡献的优势

从测算结果来看，钦州市1996—2019年间资本投入产出弹性系数为0.7739，表明一单位资本投入将增加0.7739单位的农业总产出，远高于全国平均水平，说明钦州市进一步扩大农业资本投入，对推动农业总产出的增长将更有效率，能够充分发挥其对农业总产出高边际贡献的优势。

4.3 未来应持续加大农业科技的研发投入力度，积极探索政产学研的农业发展模式

钦州市各个时期的农业科技进步贡献率波动较大，表明各个时期的农业科技发展缺乏稳定性，由于科技发展存在一个明显的储备周期，因此政府未来应持续加大对农业科技的研发投入，从而实现其对农业经济增长的持续稳步贡献。此外，政府应积极探索政产学研的农业发展模式，即由政府、农业企业、农户和高校科研单位所组建的农业科技创新联合体。其中，政府扮演领导角色，为产学研提供一个良好的农业科技创新平台，同时也为农业科技研发注入资金。而企业和农户则将市场需求反映给政府部门，或直接委托给高校科研单位，由其负责研发工作，发挥各自优势，促进农业科技进步。