受限管道空间内压壁机器人控制方法研究
2022-12-27徐炳辉李建华卫永刚
徐炳辉,张 岩,李建华,卫永刚,张 鹏
(国能朔黄铁路发展有限责任公司,山西 忻州 03400)
由于尺寸限制,管道的内部空间通常是人类无法接近的。因此,开发能够在狭窄、黑暗和弯曲的管道内表面行进的作业机器人是一个重要的研究领域。管内作业机器人的研究和开发已经持续多年,但还没有完全开发出可替代传统检测手段的机器人[1]。管道内部空间具有几何约束,作业机器人必须适应这些约束。约束变量包括管道的直径、曲率和倾斜度。管内机器人还需要能够适应管道内障碍物或锈蚀引起的不均匀内表面条件。图1给出了其中一些管道几何变化示意图,为了成功地在各种管道内执行作业,机器人需要适应这些变化。
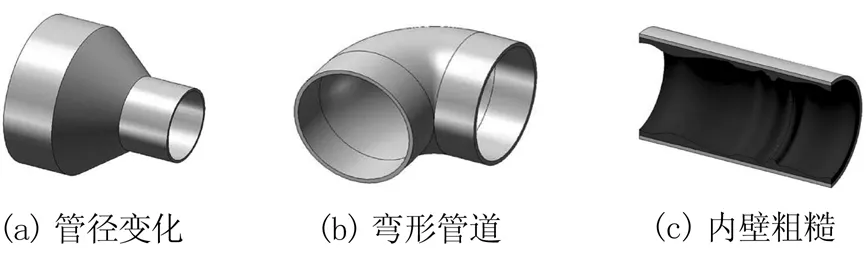
图1 管道几何变化
管内机器人应与管道内表面保持充分接触,以防止滑动或碰撞,尤其是在垂直方向上。机器人还应具有适应管道直径变化的能力,以避免与管壁失去接触。因此,大多数管内机器人需要调整其身体位置以适应不同的管道直径。机器人适应直径变化的方法可以分为被动和主动方法。被动方法可由弹簧等弹性元件支撑的连杆结构实现[2]。被动方法的优点是可以平滑地适应管道直径变化,不需要考虑对法向力的独立控制。然而,在单一被动方法下机器人通常无法适应大范围的直径变化,并且在必要时无法实现法向力控制[3]。另外,主动方法更为复杂,但在法向力控制的情况下机器人工作也更为稳健[4]。由于被动方法的诸多优点,许多学者使用一些被动元件来辅助主动法向力控制系统。有些机器人可以在没有任何自适应机构的情况下适应管道直径变化。例如,蠕动型机器人可以适应微小的直径变化,而无须使用额外的机构[5]。带有磁性车轮的机器人能够保持钢管内壁和车轮本身之间的磁吸接触,因此它们也不需要适应直径变化[6]。
管道中的曲线可能是机器人行进的主要障碍。弯管限制了机器人的身体形状,如长刚体型机器人无法通过弯型管道,需要驱动和控制每个车轮才可能实现弯管穿行。一些研究通过计算给定曲率下每个车轮或履带所需的速度或力,来解决这些问题[7]。文献[8]介绍了一种控制方法,其中只有主动轮驱动机器人,而其他车轮可以在曲线上自由移动。但为了计算机器人的速度或力,必须知道所使用管道的曲率半径。另外的解决方案是使用摄像机系统、光源跟随,或者使用如模糊控制等更复杂的控制方法[9-10]。
管道的倾斜是机器人行进的另一个主要障碍,因为不同的倾斜度需要不同的法向力。倾斜度不是普通管内机器人的运动问题,而是机器人在使用主动适应方法时效率和能量需求问题。如果机器人不能适应管道的各种倾斜,则在管道中移动时需保持恒定的法向力。在这种情况下,机器人可能会消耗更多的能量[11-12]。
考虑以上所述,提出了一种压壁式机器人,该机器人能够适应管道直径的变化,并通过简单的法向力控制和姿态控制方法成功地穿行弯曲管道。压壁机构使用主动和部分被动方法来适应管道内表面的几何变化。基于管道倾斜度估算提出了一种增强的法向力控制方法来补偿这些倾斜。如果没有法向力控制,机器人可能需要对墙壁施加更大的法向力,以便在遇到倾斜管道时不会滑动。但是,如果对法向力控制以匹配管道倾斜变化,则机器人不必不断在内壁上施加过大的力,从而降低功耗。
本文的其余部分结构如下:第一节介绍了机器人的硬件结构,包括直径变化自适应机构和驱动模块;在第二节中,描述了法向力控制和姿态控制方法;第三节进行了实验分析;第四节对全文进行总结。
1 机器人硬件结构
如图2所示,机器人由三部分组成:中央模块、履带模块和压壁机构。压壁机构和履带模块对称连接于中央模块上,相距120°。中央模块扩展或收缩压壁机构以适应管道直径的变化。履带模块围绕压壁机构自由旋转,以保持与管壁表面的接触。由ATMEGA128单片机和惯性测量单元(IMU)组成的控制单元连接到机器人的中央模块。机器人的最大速度为2.5m/min,重11kg。机器人能够穿过直径为80~350cm的管道。

图2 机器人样机
1.1 压壁机构
机器人的主要部件由带制动器的主动压壁机构和被动弹簧组成,主动压壁机构根据管道直径变化调整机器人。由于压壁机构沿径向移动,当机器人通过不平表面时,不会施加变形力。压壁连杆之间的长度比为2∶1,以提供其最大运动范围。如图3所示,该机构与具有左右螺纹的丝杠相连。位于连接器和螺钉螺母之间的可压缩弹簧有助于克服行进障碍。丝杠可以激活两个螺钉螺母,使它们彼此移动得更远或更近,使得机器人能够扩展或收缩压壁机构。此外,齿轮传动系统将直流电机的功率传输给三个丝杠,使它们能够同步旋转。
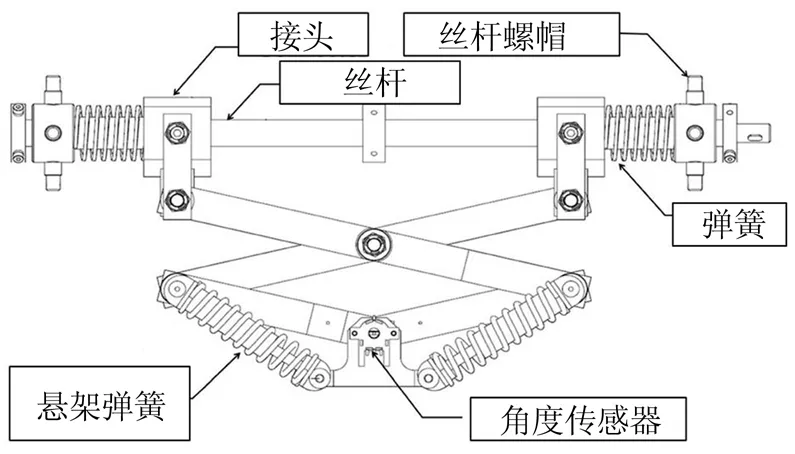
图3 压壁机构
1.2 履带模块
每个履带模块由三部分组成:前、后履带,以及一个柔性主动接头。如图4所示,柔性主动接头由无线电控制(RC)伺服电机和扭转弹簧组成。RC伺服电机连接至后履带,扭转弹簧连接至电机和前履带。柔性接头使得机器人可适应不平的表面。图5显示了机器人在凹凸表面上行驶时柔性接头的动作状态。当机器人通过突出物时,RC伺服电机调整旋转角度,以保持正面履带和管道之间的接触,如图5(a)所示。如图5(b)所示,通过凹形表面时,接头使履带模块折叠,使其与表面保持接触。履带模块通过无约束旋转接头连接到压壁机构,允许其自由旋转。即使管道内壁与机器人不平行,履带仍然被动接触与管壁接触。履带模块的这两个功能有助于机器人与管壁之间形成更大的接触面积,从而增强机器人克服障碍的能力。
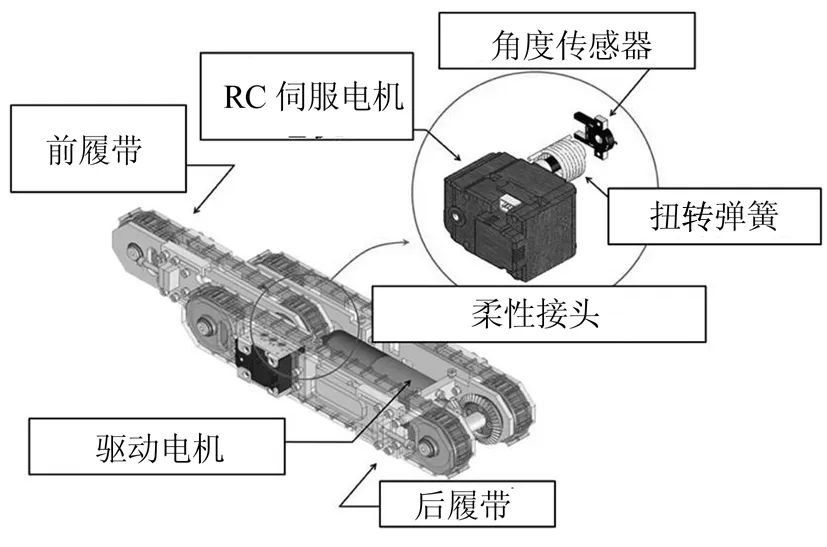
图4 柔性接头
2 控制方法
机器人能够通过法向力控制和姿态控制两种简单的控制方法,实现穿越水平、垂直和弯曲管道。机器人在不使用压力传感器的情况下估计履带模块和管道内壁之间的法向力。姿态控制使得机器人可在一个弯曲的管道内移动,而不需要提供管道的几何信息。还可估计管道的倾斜度,并根据倾斜度控制机器人法向力。

图5 柔性接头通过凹凸表面时动作状态
2.1 法向力控制
在驱动机构和管道内壁之间的法向力控制对于机器人牵引非常重要。通过观察作用在压壁机构上的力之间的关系,在不使用压力传感器的情况下估计法向力。弹簧施加的恢复力和施加在压壁上的法向力如图6所示。通过静态分析,得出法向力和恢复力之间的关系:
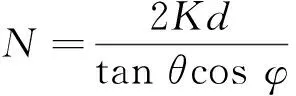
(1)
其中K为刚度,d为悬架弹簧的位移,θ为压壁机构的半夹角,φ为履带模块相对于内壁的旋转角度。两个角度传感器位于压壁的两个闭合端,用于检测角度θ1和θ2。使用以下公式计算角度θ和φ:
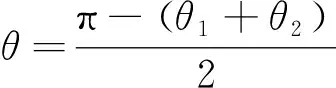
(2)
φ=θ2-θ1
(3)
使用电机编码器计数值和夹角θ计算弹簧位移。因为切线函数位于式(1)中分母部分,所以机构有不可控制和不可检测的点。如果角度θ为零,则无法估计法向力。另外,如果θ为90°,则机器人无法控制法向力。然而,连杆物理尺寸使得奇异点不存在。将螺钉的转数乘丝杠的螺距,可以计算螺钉螺母的位置。当弹簧未被压缩时,通过使用弹簧的自由长度来计算连接器的位置。另外,还可以使用夹角θ计算弹簧压缩时接头的位置。弹簧的位移通过下式计算:
d=(pscrew×Ω+d0)-Lsinθ
(4)
其中pscrew是节距长度,Ω是丝杠的转数,d0是弹簧的自由长度,L是连杆的长度。机器人通过使用式(1)和式(4)测量并维持法向力。
2.2 姿态控制
姿态控制对于沿弯曲管道移动的机器人非常重要。以前的姿态控制方法需要所穿行管道的信息,通常使用视觉传感器收集此信息。然而,所提出的机器人不需要任何关于弯管的信息。通过姿态控制使得机器人在通过任何管道(包括弯管)时保持自身平衡。
当机器人在直管中移动,且每条履带的速度相同且位置平齐时,机器人是对齐姿态。如图7所示,当机器人必须克服障碍物或通过弯管移动时,则机器人的姿态会发生变化,机器人的履带位置不是平齐,但旋转接头使履带与管道内壁保持接触,机器人为非对齐姿态。如2.1节所述,当机器人为非对齐姿态时,与对齐姿态之间的偏差由履带模块的旋转角度决定。当机器人通过弯道时,控制单元比较每个履带的旋转角度φ,允许履带以不同的速度移动,直到旋转角度φ完全相同,这个过程以履带旋转角度偏差为反馈量,使用PI控制电机转速来实现。例如,中央模块后面的履带的速度比图7中的前导履带的速度快。这些不同的速度会一直保持,直到机器人的姿态对齐为止。
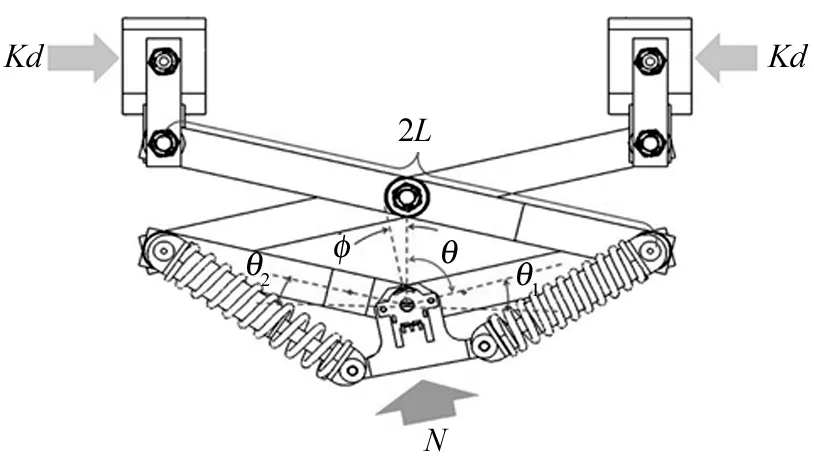
图6 压壁机构受力分析

图7 姿态控制示意图
2.3 管道倾角估算
如前所述,机器人的中央模块并不总是与管道平行,需要估计机器人跟管道的相对方向。如图8所示,使用截面P穿过三个接触点和机器人中心,用以表示机器人的姿态。P0表示机器人姿态对齐时的理想截面。P1和P2表示机器人未对齐的姿态。机器人的姿态定义为绕两个轴旋转程度;P1表示P0以角度α绕x轴旋转,P2表示P1以角度β绕z′轴旋转。管道和截面之间的角度称为旋转角度φ。由于履带位于截面P2边界的椭圆上,因此履带的旋转角度根据角度α和β而变化。履带的旋转角度与接触点位于y′轴上时的角度α相同,但当接触点位于x轴上时为零。检测到的履带旋转角度根据角度β从α到-α之间变化,并以2π为周期。因此假设履带的旋转角度可以用余弦函数表示,如下所示:
φi=Acos [ψ+120°×(i-1)],(i=1,2,3)
(5)
其中ψ是绕z′轴的特定旋转角度,i是履带号。三个检测到的角度位于余弦图上,如图9所示。由于履带模块在中央模块上相距120°,因此检测到的角度以120°相位角排列。可以使用相位角从履带的旋转角度计算截面的旋转角度:
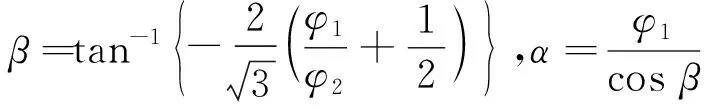
(6)
从检测到的角度φ获得两个旋转角度α和β,角度α和β描述了机器人自身相对于管道的姿态。由于获得管道倾角需要相对于管道的姿态和相对于地面的方向,因此机器人使用三轴加速计检测重力方向。旋转矩阵表示姿态和方向,矩阵运算用于获取管道相对于地面的方向:

2.4 所需法向力计算
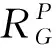
(8)
(9)
使用式(9)获得适当的法向力,其中Fz表示z轴上的力,m表示机器人的重量,g表示重力加速度。然而,式(9)存在一个问题:当Θ=0°时,法向力变为零。因此,对式(9)进行了修改,如下所示:
N=(Nmax-mg)sinΘ+mg
(10)
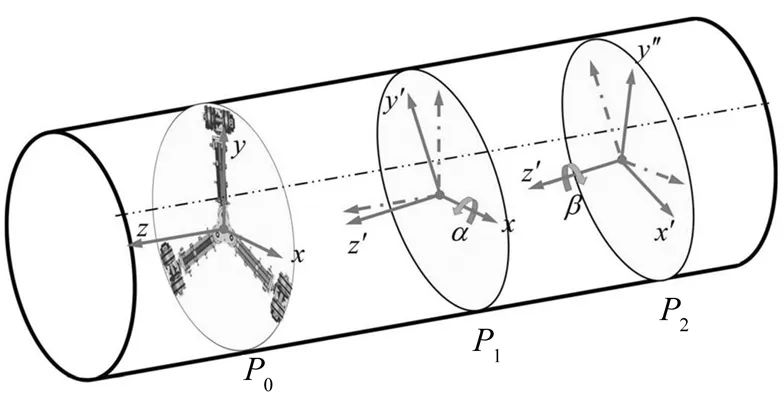
图8 机器人在管道内方位
其中Nmax是最大法向力,该力也是攀爬垂直管道所需的力。
在计算适当的法向力后,可维持机器人穿行所需的力。通过这个过程,机器人不断适应管道的倾斜变化。

图9 机器人角度检测
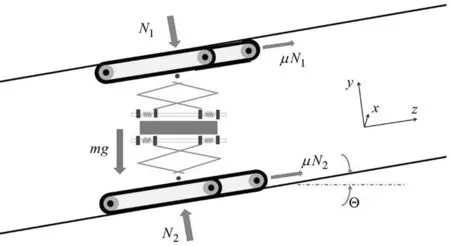
图10 机器人在斜管中受力情况
3 实 验
如图11所示,为进行试验,将各种管道串联起来,使用透明管道观察机器人工作情况。机器人使用来自IMU传感器的数据来检测重力方向。选择摩擦系数为0.4,这是通常情况的四分之一,从而将实验条件设置为比实际条件更严格,可证明机器人提供了足够的穿行能力。图12给出了管道的实际倾斜角度和估计倾斜角度。实际倾斜度是根据管道的长度和高度计算出来的。由于试验中使用的弯管不存在连续曲率,因此实际倾角是离散的。几何约束瞬间发生变化,每当机器人通过这些离散变化点时,机器人就会改变其尺寸。由于机器人的姿态会影响其相对于管道的相对方向的计算,因此弯曲管道中的倾斜估计会发生波动。垂直管道略微倾斜,当机器人垂直移动时,管道的估计倾斜度不是90°,如图12(b)所示。

图11 实验管道
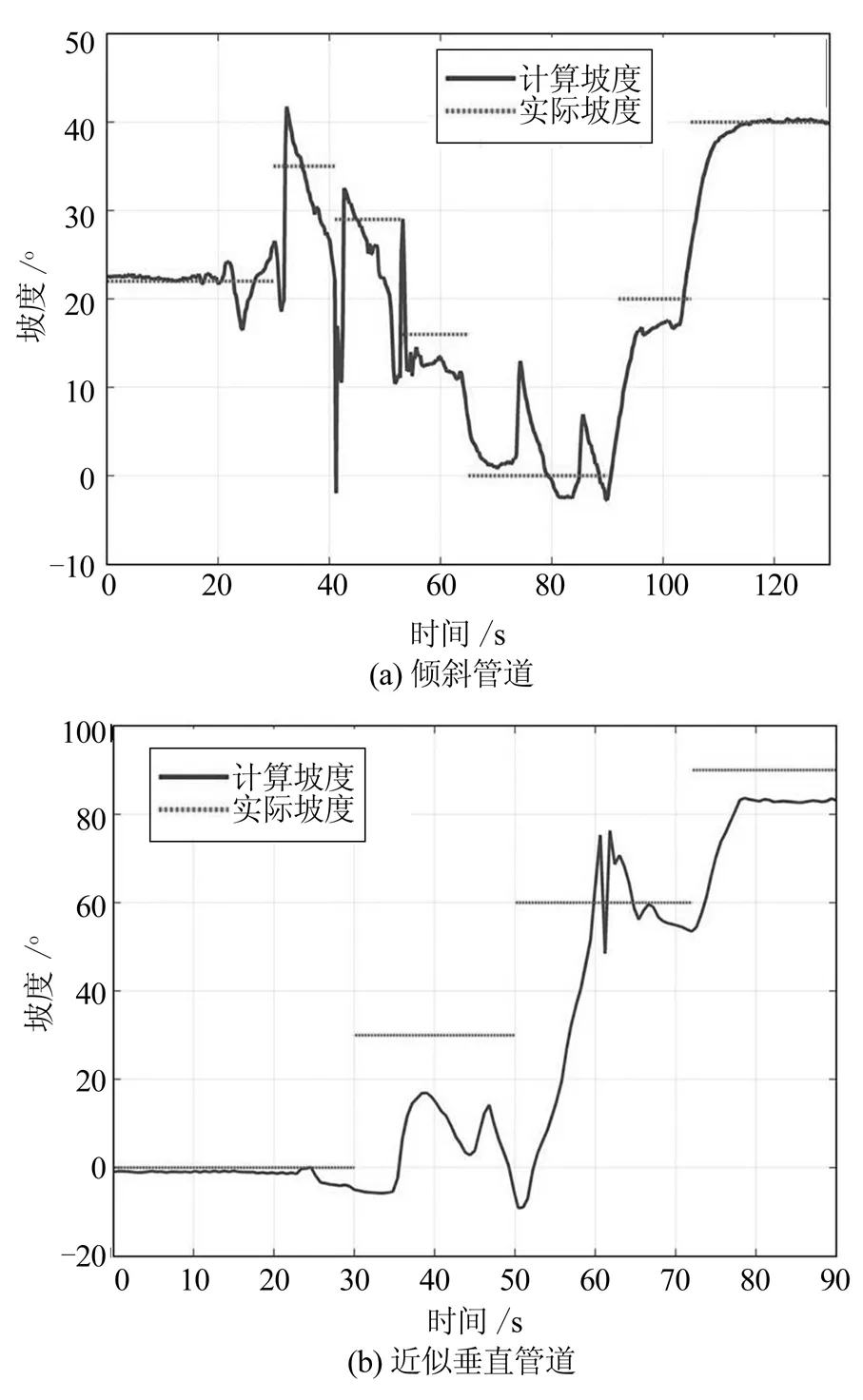
图12 实验管道角度评估
图13(a)和(b)分别显示了机器人在近似垂直管道中是否使用姿势控制和法向力控制移动时的功耗图。功耗记录了机器人运动过程中的所有电机负荷信息。未使用倾角估计算法时,机器人在90s内消耗3675.6 J能量以维持其法向力。使用倾角估计算法时,机器人在相同的时间内使用3254.4 J。这些结果表明,使用所提出的方法减少了机器人约11.46%的能量消耗。在这两种情况下,机器人在初始化期间消耗量为20W/s。水平管道的功耗降低了约20%。因为最大法向力是为垂直管定义的,计算出的和最大法向力之间的差异随着估计倾斜度的增加而减小,所以弯管中的消耗量变得相似。法向力作为外部扭矩施加在中央模块和履带模块上,垂直管道的功耗降低较小。因此,驱动器需要更多的动力以在相同的速度下维持更大的法向力。尽管最大法向力因管道摩擦系数而异,但所提出方法通过控制法向力有助于减少机器人电力消耗。
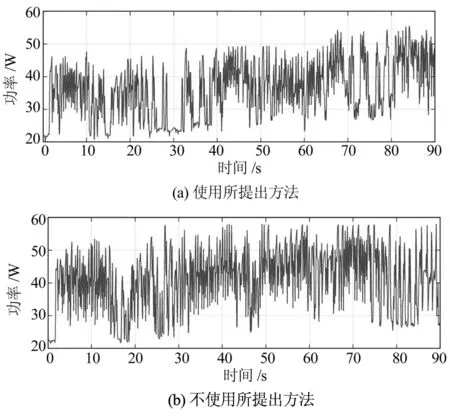
图13 不同控制下机器人功耗
4 结 论
提出了一种能够适应管径、中心曲率和管道倾角变化的压壁式机器人,并提出一种法向力控制和姿态控制方法。实验结果表明,所提出的控制方法工作良好,通过适当控制法向力,机器人能够降低功耗以及部件上的应力。未来的研究将集中在一个完全自主的作业机器人和多模块机器人系统,以实现在没有任何外部援助或远程控制的情况下进行受限管道空间内检测作业。
