基于相对轨道根数计算的测绘卫星单点定位研究
2022-12-27赵峻天
赵峻天
(陕西能源职业技术学院,陕西 咸阳 712000)
卫星轨道需要通过单点定位方法精确获取,此过程结合IGS和钟差,利用多个GPS接收器实现载波相位的观测,预估卫星地面站的立体坐标、接收器的钟差以及电离层等参数,单点定位技术现今已经广泛应用于航空、海洋等诸多领域的相关测量[1-3]。
卫星的运行轨道对卫星定位存在直接影响,但是当前的测绘卫星定位方法普遍存在轨道信息掌握不全面问题,导致定位出现较大偏差。为此,提出基于相对轨道根数计算的测绘卫星单点定位方法。将卫星的轨道以及飞行状态作为轨道运行参数[4]。为实现测绘卫星单点定位、准确定位卫星单点位置,构建J2摄动模型,利用该模型预测卫星轨道根数,以此判断所需定位卫星相对轨道状态,再缩小定位范围,在卫星所处轨道中,实现测绘卫星的单点定位。
1 基于相对轨道根数计算的测绘卫星单点定位方法
1.1 基于J2摄动模型的卫星轨道根数预测方法
1.1.1 计算六根数变化率
设定初始轨道六根数为[φ0,φ0,j0,η0,ϖ0,N0],轨道六根数变化率计算公式为:
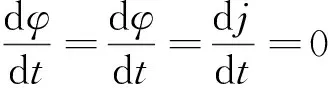
(1)
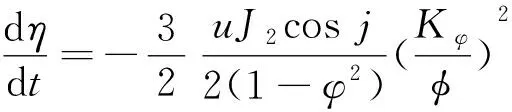
(2)
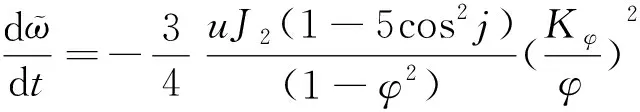
(3)
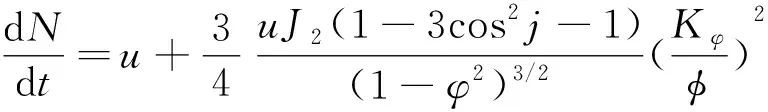
(4)
式中,u为卫星在轨道路程的变化率;Kφ为地球平均赤道半径;d表示求导。
1.1.2 计算t时刻轨道六根数
在非未知t时刻中,计算随机时刻t的轨道六根数:
φ=φ0
(5)
φ=φ0
(6)
j=j0
(7)
η=j0+uη(t-t0)
(8)
ϖ=ϖ0+uϖ(t-t0)
(9)
N=N0+uN(t-t0)
(10)
使用上式可获取随机时刻的轨道六根数[φ,φ,j,η,ϖ,N],以此掌握卫星所在轨道,缩小卫星单点定位范围。
1.2 基于相对轨道根数的卫星单点位置预测
1.2.1 卫星运动方程
按照上小节所预测的卫星运动轨道信息,在卫星轨道(图1)中,设定天球坐标系为O-XYZ,坐标系的原点为地球质心点[5-7]。
由于地球自身质量远大于卫星质量,因此卫星对地球的引力的干扰是可以忽略不计的[8]。

(11)
式中,N为地球质量,n为卫星的质量,矢量s为起始点为O的卫星的位置,H为卫星所在位置的高度。
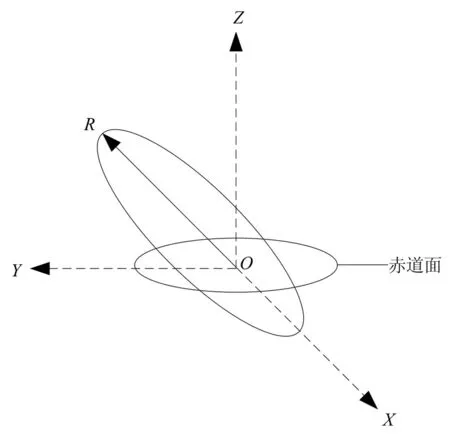
图1 卫星轨道面
式(11)简化成:
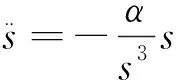
(12)
α=HN
(13)
其中,s3是卫星轨道位置矢量s的模,表示地心距(地心向径),则:
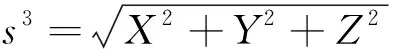
(14)
转换成标量模式:
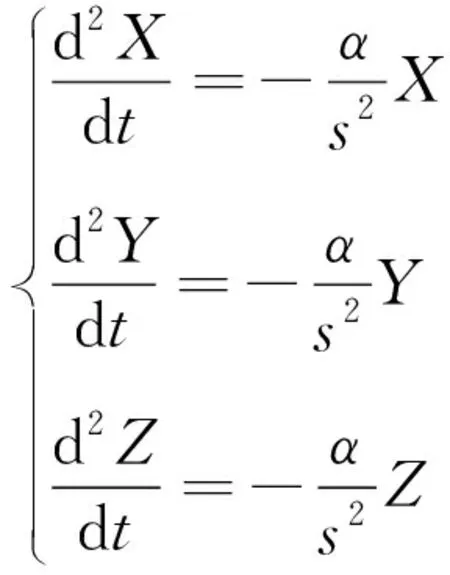
(15)
如上述所示,卫星运动方程属于三元二阶联立微分方程组,必须使用6个积分常数求解方程[9-11]。
卫星轨道极坐标方程积分为:
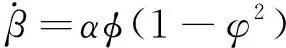
(16)

使用活力公式将其转换成:

(17)
式中,β为活力转换后卫星轨道极坐标方程。
可获取:

(18)
式中,卫星穿过近地点的平均角速度是m。为了利于积分,使用辅助变量D,其代表偏近点角。
将和椭圆中心连线、近地点方向的夹角设成偏近地角F。则:
cosF=scosg+φφ
(19)
其中,g是真近地角。使用椭圆轨道方程能够获取:
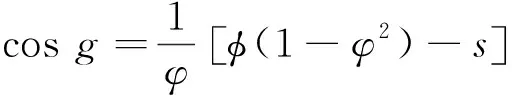
(20)
以此导出的表达式是:
φcosF=φ-s
(21)
将上式导进位置微分方程,可获取:
(22)
积分可获取:
F-φsinF=mt+H0
(23)
式中,积分常数为H0。
式(23)即为开普勒积分,属于开普勒方程。其能够描述偏近地角F与时间的关系。
若F的值是0,ε便表示卫星穿过近地点的时间,计算过程中,使用平近点角N取代ε:
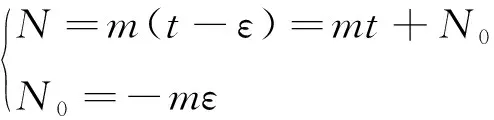
(24)
式中,若初始时刻t的值为0,N0为卫星的平近点角。
1.2.2 卫星星历计算
按照卫星的轨道根数,分析卫星在某时间中的方位和速度,此过程即为卫星星历计算[12]。开普勒方程是:
F-φsinF=N
(25)
式(25)属于超越方程,使用迭代法可求解F。将方程两侧微分,转换为:

(26)
设置初始值F0=N,迭代方法是:

(27)
迭代停止条件是:
(28)
其中,Ft、Nt依次是t时刻的偏近地角、平近点角。
使用椭圆的圆锥曲线方程,能够获取真近地角g与偏近地角F的关系:

(29)
1.2.3 卫星单点位置和速度计算
根据卫星的正常运行情况可以推测,在轨道平面上卫星以顺时针方向按照椭圆形轨迹飞行[13-15]。设定当时间为t时,对应的卫星位置为s,并设定该位置为定向矢量。若近地点方向的单位矢量为Q,以及与之垂直的单位矢量为P,则卫星的位置矢量可表示为:
s(X,Y,Z)=scosg·Q+ssing·P
(30)
导进cosg、sing,获取:
s(X,Y,Z)=
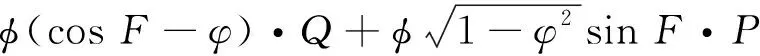
(31)
通过卫星位置微分计算卫星的速度:
(32)
2 实验设计与结果分析
为测试所提方法的有效性,使用国际空间站的观测数据作为所提方法测试数据。将所提方法的测试数据与实际数据进行比对,以此判断研究方法的应用效果。
本次实验数据采用MGEX网所采集到的BDS和GPS、观测时段为2020年1月1日-6月30日的数据,本次实验的测站分布如图2所示。
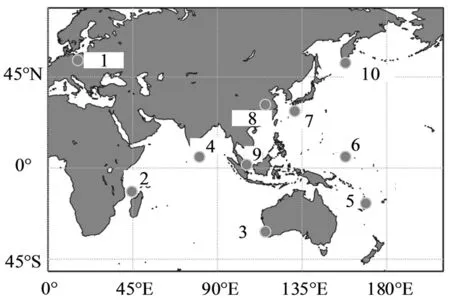
图2 测站分布图
利用所提方法在以上测站位置对卫星进行定位。本实验主要对N(北)、S(南)、E(东)三个方向进行定位,测试时长为14h,多个测站位置的定位平均误差(m)结果如下:
根据图3~图5的实验结果可知,所提方法在N、S、E三个方向的定位结果精度较高。N方向的定位误差在±0.05m范围内;S方向定位误差最为理想,在14h的测试时间段内,其误差始终在±0.02m范围内;E方向定位误差也可保持在±0.05m范围内。以上数据表明,所提方法的应用精度偏高,应用效果较优。

图3 N方向定位误差
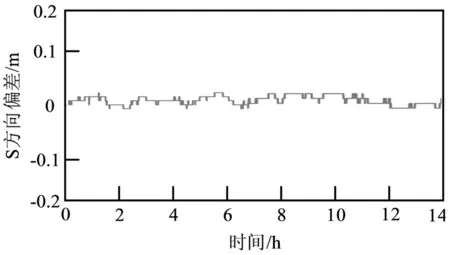
图4 S方向定位误差
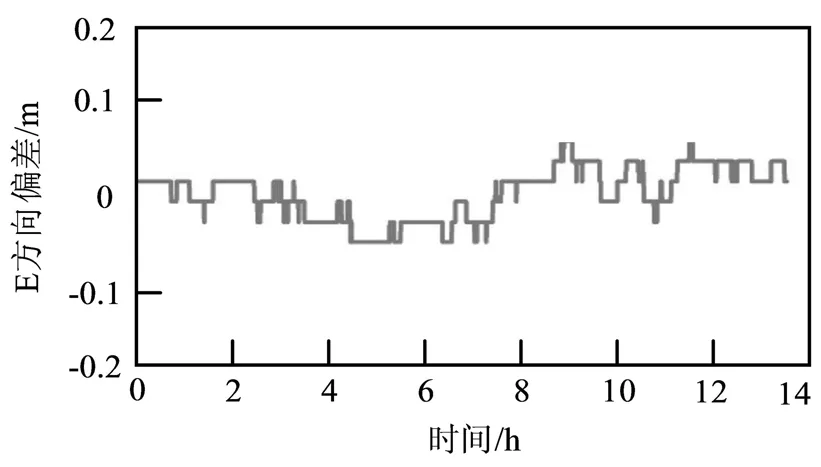
图5 E方向定位误差
所提方法在定位测绘卫星位置后,对卫星所在轨道进行预测,预测误差的标准主要通过均值、均方值、最大值体现。在某阶段中,预测误差绝对值的平均值即为预测误差均值;预测误差平方的均值是均方值;预测误差绝对值的最大值即为最大误差。因为均方值常用于描述误差分布状况,说服力显著,所以,使用预测误差均方值描述研究方法的卫星所在轨道预测性能。
预测卫星分别是近地卫星、中高度卫星、地球同步卫星。在不同时间段中,研究方法对三种卫星所在轨道预测结果如图6~图11所示。

图6 卫星所在轨道半长轴预测结果

图7 卫星所在轨道偏心率预测结果

图8 卫星所在轨道倾角预测结果

图9 卫星所在轨道升交点赤径预测结果

图10 卫星所在轨道近地点幅角预测结果
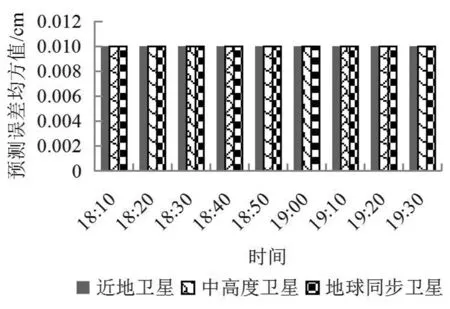
图11 卫星所在轨道平近点角预测结果
由图6~图11可知,所提方法在预测三种卫星所在轨道根数(轨道半长轴、偏心率、轨道倾角、升交点赤径、近地点幅角、平近点角)时,预测误差均方值均低于0.04cm,预测误差极小,由此可见,研究方法对卫星所在轨道预测结果可信。
以上述实验数据为基准,再使用研究方法单点定位三种卫星,三种卫星的位置定位结果如图12~图14所示。

图12 近地卫星定位误差均方值
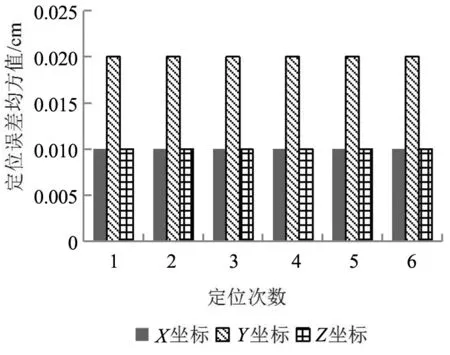
图13 中高度卫星定位误差均方值

图14 地球同步卫星定位误差均方值
由图12~图14可知,所提方法在定位三种测绘卫星时,定位误差均方值最大值是0.02cm,可满足卫星单点定位应用需求。
3 结 论
以测绘卫星单点定位为研究内容,提出基于相对轨道根数计算的测绘卫星单点定位方法。并为了测试所提方法的可应用性,使用其对三种类型的卫星轨道预测、位置定位。测试结果为:
(1)所提方法在N、S、E三个方向的多个测站位置定位平均误差的波动范围为±0.05m,定位误差极小;
(2)所提方法在预测三种卫星所在轨道根数(轨道半长轴、偏心率、轨道倾角、升交点赤径、近地点幅角、平近点角)时,预测误差极小;
(3)所提方法在定位三种测绘卫星时,定位误差均方值极小,可准确定位测绘卫星位置。
